pdf: https://arxiv.org/abs/2211.10438

---

특징)

• W8A8 → Weight 8-bit, Activation 8-bit → LLM의 모든 matrix multiplication에서 weight, activation을 INT 8!
• PTQ → Training Free, Accuracy preserving

의의)

• Weight Quantization은 쉬우나, Activation Quantization은 어렵다 → SmoothQuant: Activation Outlier를 smoothing
• 속도 향상: 최대 1.56배, 메모리 감소: 최대 2배 (정확도 손실 거의 없이)
• 530B LLM을 single node로 서빙할 수 있게 함
• 다양한 양자화 체계와 호환 → 3가지 efficiency-level 설정 구현:
  • Hardware-efficient: Pytorch에서 최대 1.51배 속도 향상 & 1.96베 메모리 절약 & 성능 유지
  • 구현하기 쉬움: FasterTransformer에 통합 → 최대 1.56배 속도 향상 & FP16에 비해 메모리 사용량 절반으로 줄임
  • 큰 모델 서빙 가능 → 530B 모델을 8-GPU node로 서빙 가능

배경)

LLM의 activation은 quantization 하기 어렵다 → 6.7B 이상 넘어가면, 체계적인 outlier가 activation에서 많이 발생 → 큰 quantization error & accuracy degration 발생

논문의 방법론을 사용하게 된 동기)

1. Weight보다 Activation은 quantization하기 어려움: Weight 분포는 꽤 uniform & flat → Quantization하기 쉬움

2. 이상치가 quantization을 어렵게 함

   Activation에서 이상치의 크기는 대부분의 activation value보다 100배 이상 크다 → 이상치가 maximum magnitude 측정을 지배 → 범위 구간이 매우 넓어지고, 이는 양자화 퀄리티를 낮춘다

3. 이상치가 fixed channel에서 지속됨

   '채널의 일부에서 outlier 발생' & '만약 한 채널에서 outlier 발생하면, 모든 토큰에서 outlier 발생'

   • 주어진 토큰에서 채널 간의 분산이 큼 → 몇몇 채널에서는 activation이 매우 크고, 대부분은 작음
   • 주어진 채널에서 토큰 간의 분산은 작음 → 이상치 채널들은 지속적으로 큼

   따라서, channel 단위(per-channel) 양자화 하는 것이 좋음 → 하지만 이는 hardware-accelerated GEMM 커널에 잘 맞지 않음

   

Preliminaries(Quantization)

▫️ Static Quantization vs Dynamic Quantization

• Static Quantization:
  • 데이터를 잘 표현하는 데이터를 일부에 대하여(calibration samples), 해당 데이터를 통해 quantization factor를 미리 계산 → Runtime동안 양자화 구간에 대해 양자화 상수를 매번 계산하지 않아도 되어서 시간 절약
  • 모든 구간에서 동일한 양자화 상수(미리 계산해둔) 사용
  • 입력 데이터 분포 변화가 대게 일정한 작업에 사용하기 좋음
• Dynamic Quantization:
  • 들어오는 데이터에 맞게 그때그때 양자화 상수 생성 → latency가 발생하지만, 정확도 상승
  • 구간마다 다른 양자화 상수(동적으로 계산하여) 사용
  • 입력 데이터 분포가 자주 변하는 작업에 사용하기 좋음

▫️ Per-tensor Quantization & Per-token Quantization & Per-channel Quantization

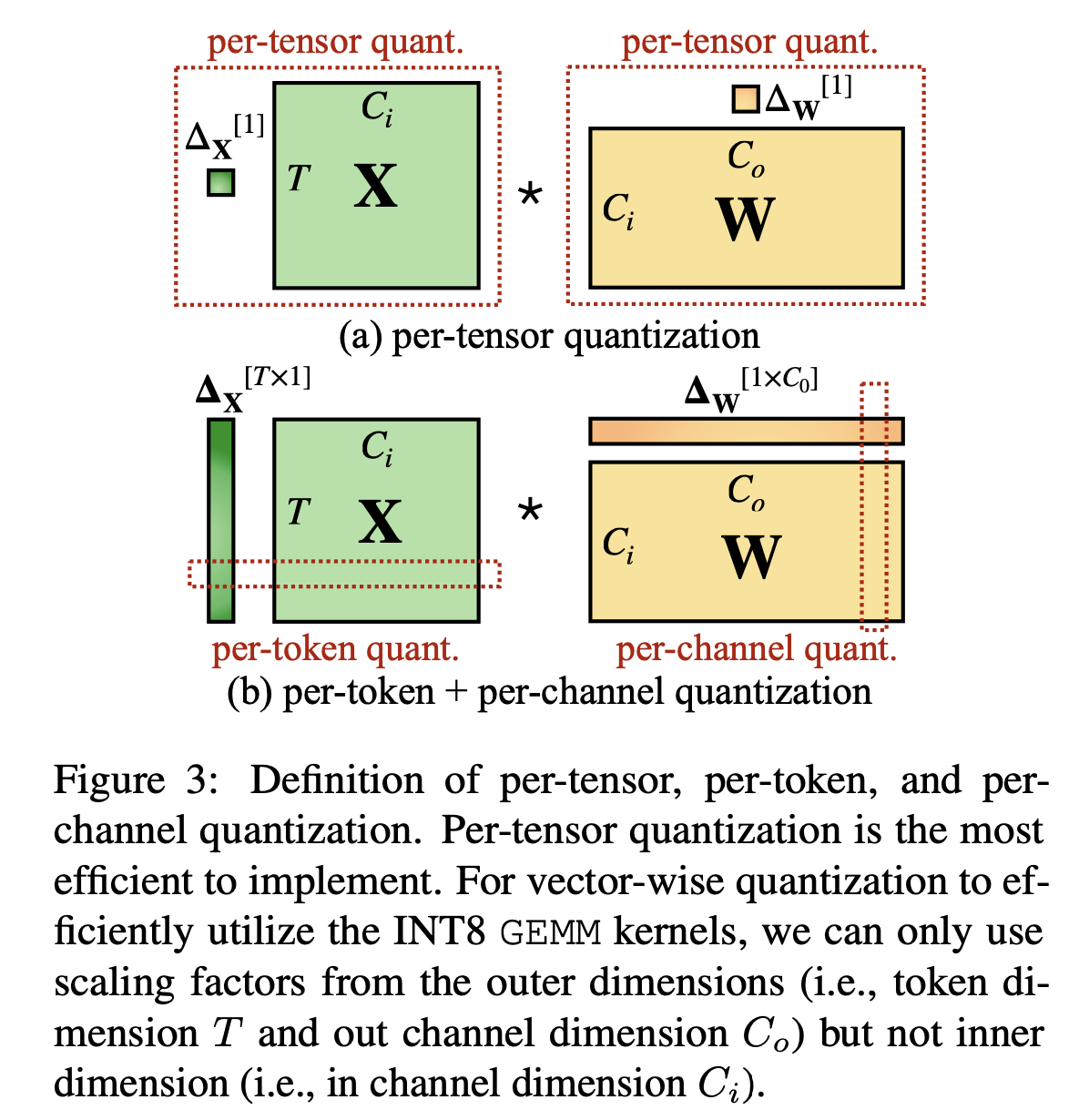
• Per-tensor: 모든 matrix에 대해서 하나의 양자화 상수 적용
• Per-token: 토큰 별로 개별 양자화 상수 적용
• Per-channel: 채널 별로 개별 양자화 상수 적용
• Group-wise: per-channel quantization의 거친 버전 → 여러 channel을 하나의 group으로 묶고, group 별로 양자화 상수 적용

SmoothQuant(본 논문의 방법론)

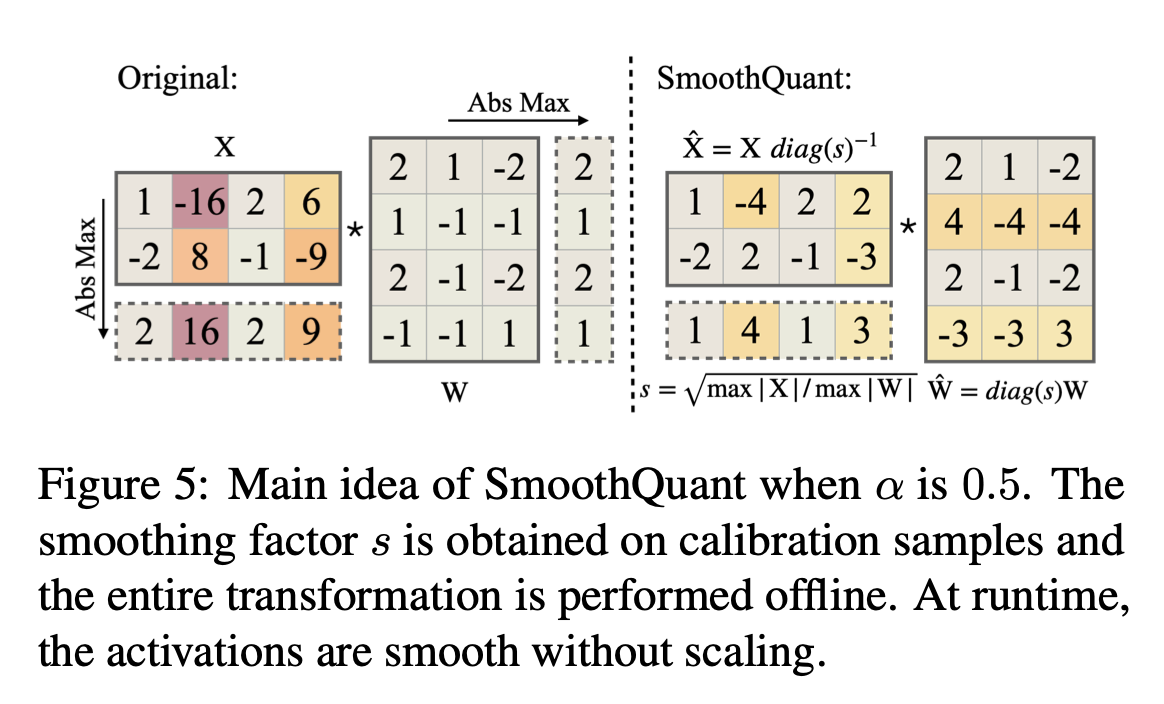
Per-channel activation quantization 대신에 per-channel smoothing factor( $s \in \R^{C_i}$)로 input activation을 나눔 → 입력 activation을 ‘smoothing’

Linear layer의 수학적 동등성을 지키기 위해 → 반대 방향으로 weight를 scaling:

설명)

$\text{diag}(s)$: s를 diagonalizing. 즉, s의 값들을 diagonal element로 갖는 square matrix
ex) $s = \begin{bmatrix}1\\2\\3\end{bmatrix} \in \R^{3} \rightarrow \text{diag}(s) = \begin{bmatrix}1, 0, 0\\0,2,0\\0,0,3\end{bmatrix} \rightarrow \text{diag}(s)^{-1} = \begin{bmatrix}\frac{1}{1}, 0, 0\\0,\frac{1}{2},0\\0,0,\frac{1}{3}\end{bmatrix}$

입력에 대해서 per-channel scaling factor를 나눠준다.

근데 원래의 식과 동일해야 하니까 W부분에 diag(s)를 곱해준다 → $Y = XW$ 값이 바뀌지 않고 유지되어야 하니까! W의 앞 부분에 diag(s)를 곱해주는 것! $Y = XW = X \text{diag(s)}^{-1}\text{diag(s)}W=\hat{X}\hat{W}$

이렇게 바꿔주면, 이제 $\hat{X}, \hat{W}$는 quantization 하기 쉬워진다!

<여기서 extra scaling을 통해 발생하는 overhead를 줄이는 방법>

위의 식에서 X는 이전 layer의 output이다. 그러니까 이 부분을 런타임 전에 미리 계산하면 runtime동안 kernel call scaling overhead가 발생하지 않음

→ $Y =XW = L_nW_n =(L_{n-1}W_{n-1} + b_{n-1})W_n$ 이라고 볼 수 있다(여기서 $L_{n-1}, W_{n-1}, b_{n-1}, L_n$: 이전 layer의 입력값, weight, bias, 현재 layer의 입력값(즉, X)

$Y = (X\text{diag}(s)^{-1}) \cdot (\text{diag}(s) W) = ((L_{n-1}W_{n-1} + b_{n-1})\text{diag}(s)^{-1}) \cdot (\text{diag}(s) W)$ 이렇게 볼 수 있으니까 scaling factor 계산을 runtime 전에 미리 해놓으면(offline), runtime동안 scaling factor로 인한 overhead는 발생하지 않는다.

Quantization difficulty를 activation에서 weight로 이동시킴

per-channel smoothing factor $s$를 통해 activation quantization difficulty를 weight에게 넘긴다!

Activation의 Quantization을 쉽게 하기 위해 per-channel smoothing factor $s$ 만들기 단계

1. $s_j = \max (|\text{X}_j|), j= 1,2,\dots, C_i$
2. 근데 이렇게 하면, 모든 quantization difficulty를 weight로 전이시키는 것 → weight에서 quantization error가 커짐
3. Weight에 대한 부분도 s에 추가 → $s_j = 1 / \max(|\text{W}_j|)$
4. 최종: $s_j = \max(|\text{X}_j|)^\alpha / \max(|\text{W}_j|)^{1-\alpha}$ . $\alpha$를 이용해서 quantization difficulty를 얼마나 activation에서 weight로 이동시킬지 정함 ( $\alpha = 0.5$ 가 difficulty를 activation과 Weight에 잘 나눈 well-balanced point.)

이 과정 속, activation의 range는 dynamic → input samples에 따라 달라짐 → Pretraining dataset의 Calibration samples을 사용해서 activation channels의 scale 추정

예시 아래 그림)

Transformer block에 SmoothQuant 적용

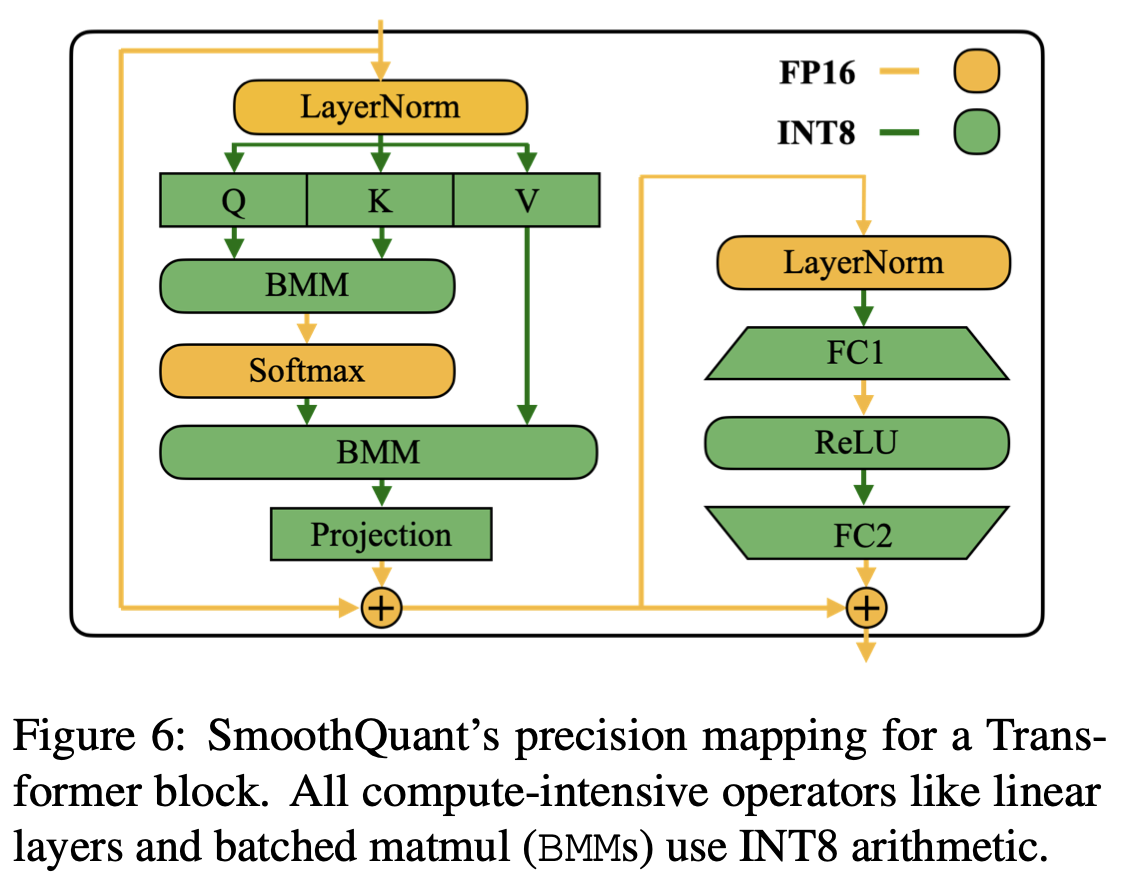
• Linear Layer, BMM in attention과 같은 계산이 많은 부분: Weight & Activation → INT 8

• 가벼운 element-wise operations(ReLU, Softmax, LayerNorm): FP16

Experiments

Activation Smoothing

$\alpha$ 정하기(sweet spot)

• OPT, BLOOM : $\alpha = 0.5$
• GLM-150B : $\alpha = 0.75$ (activation을 quantization 하기 힘든 경우)

Implementation

• Pytorch HuggingFace
• FasterTransformer
  
  

결과들

<방법론 디테일(아래)>

Accurate Quantization

<벤치마크별 비교 (아래)>

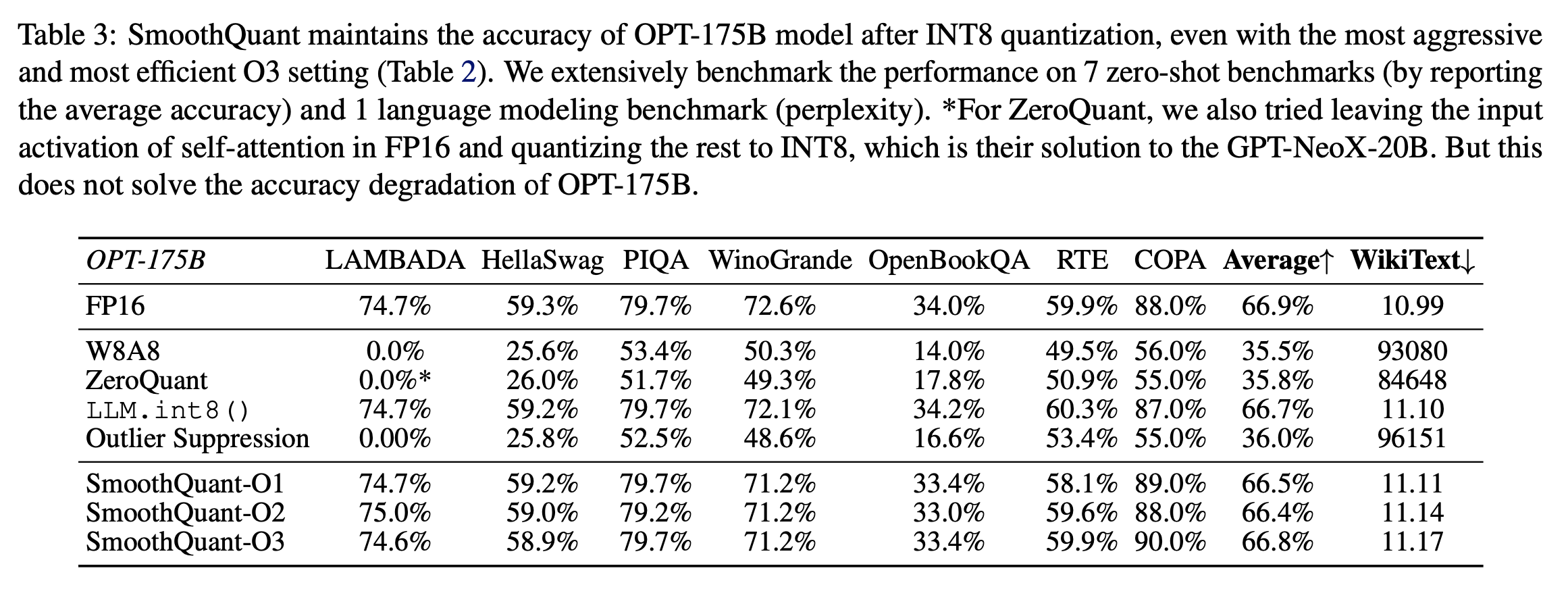
<모델별비교 (아래)>

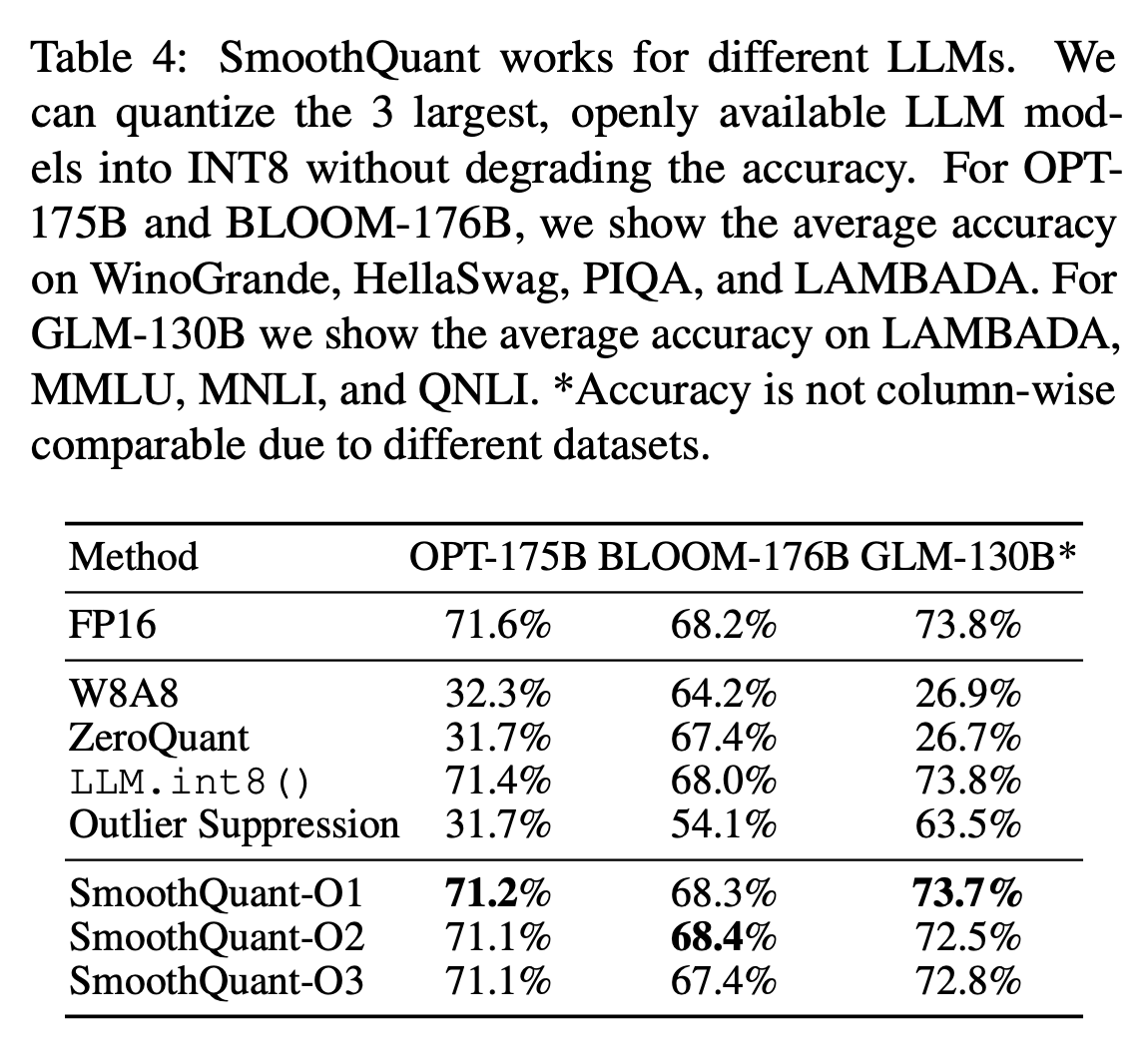
<최근 모델에 적용: SmoothQuant는 성능 손해를 최소화 하며 W8A8 quantization을 가능하게 만듦 (아래)>

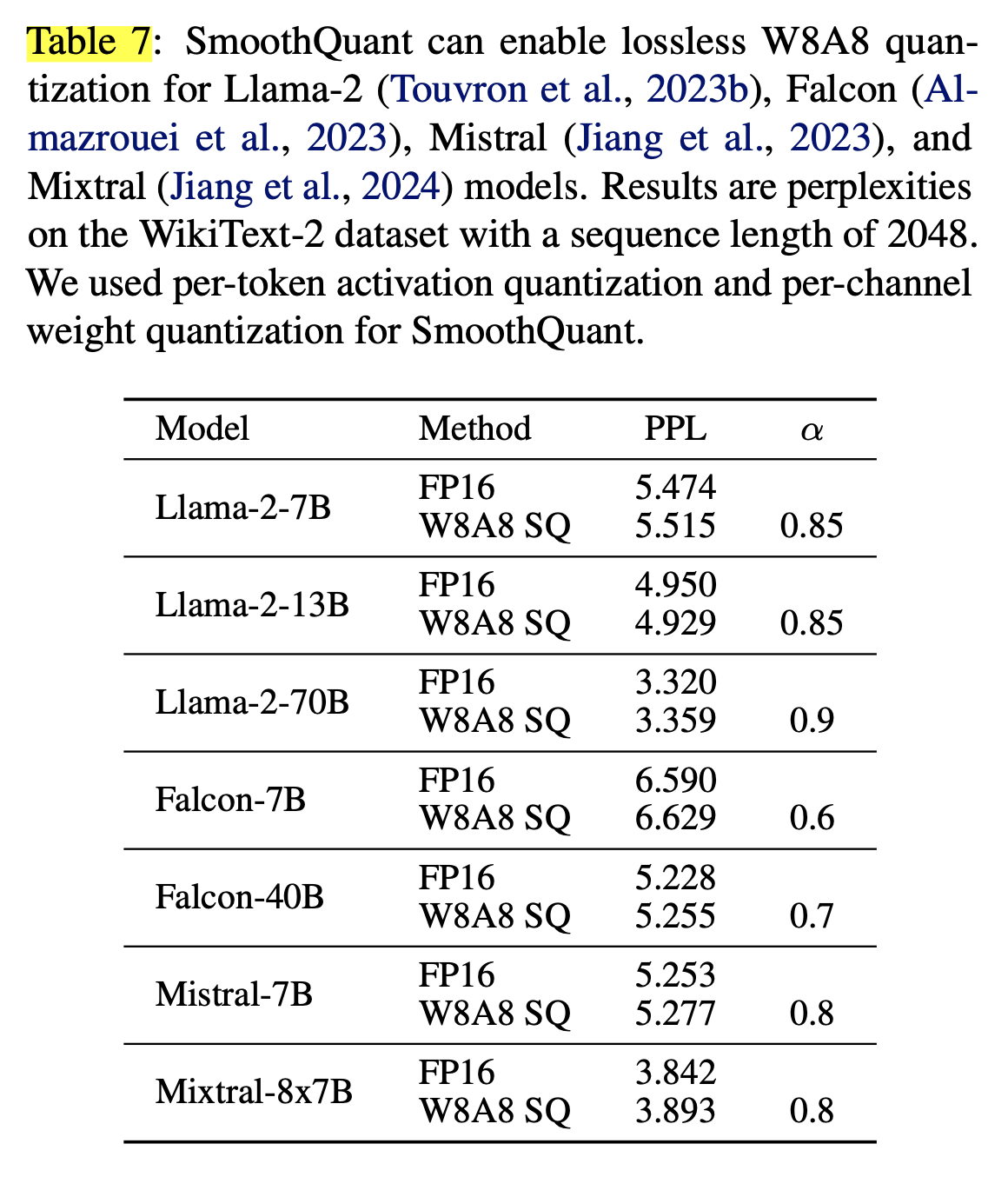
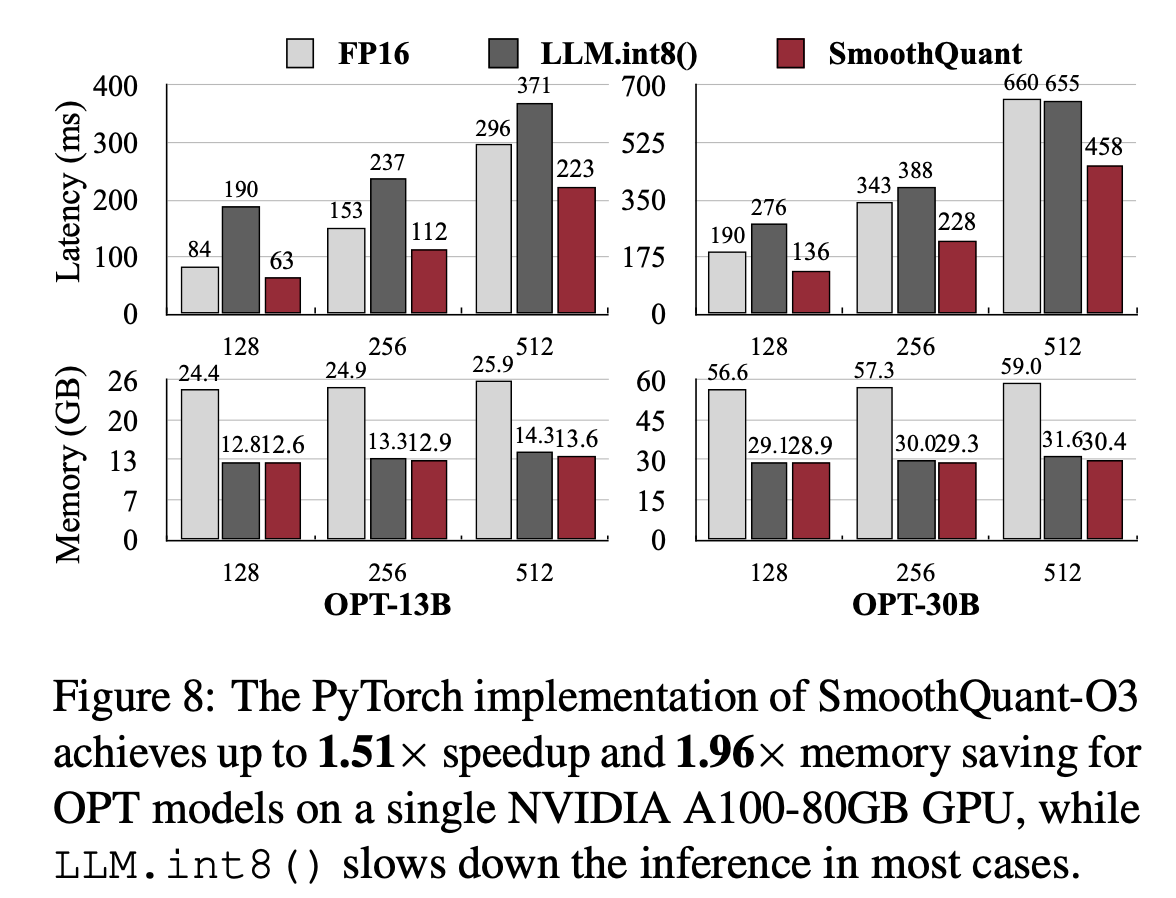
Memory Saving & SpeedUp

SmoothQuant-O3의 memory saving & speedup

설명)

1. 문장 4개가 하나의 배치이고, 이에 대한 모든 hidden state 생성의 End-to-End latency 측정 → Context Stage Latency.
2. Memory → Peak memory usage

2개의 backend에서 구현)

• PyTorch
  • 문장 4개가 하나의 배치이고, 이에 대한 모든 hidden state 생성의 End-to-End latency 측정 → Context Stage Latency.
  • Memory → Peak memory usage
  • Single GPU을 사용(HuggingFace에서 model parallelism 지원이 부족해서) → 평가 모델: OPT-6.7B, OPT-13B, OPT-30B
  • 비교)
    • 방법: SmoothQuant, LLM.int8(), FP16(base)
    • 평가 항목: inference latency, peak memory usage
    • x축: sequence length
      

• FastTransformer
  • FastTransformer에서는 Tensor-Parallelism을 원활히 수행할 수 있어서, single & multi gpu benchmark에 대해서 평가할 수 있었음
  • 비교)
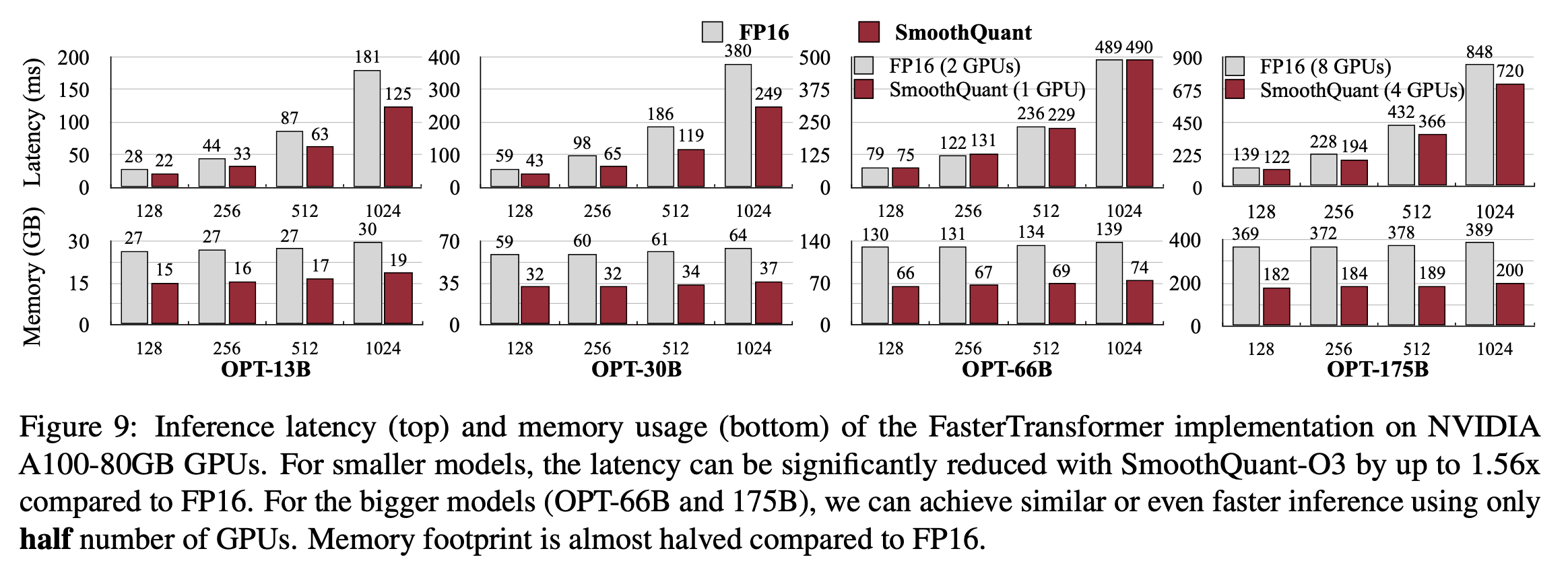
    • FastTransformer Implementation이 Pytorch implementation보다 빠름(30B의 경우 3배 이상 빠름)
    • 오른쪽을 보면, FP16과 SmoothQuant를 비교할 때 FP16에서 사용하는 gpu 수의 반만 사용하는데 latency는 비슷하거나 그 이상 → LLM serving 비용을 크게 낮출 수 있음

Ablation Study

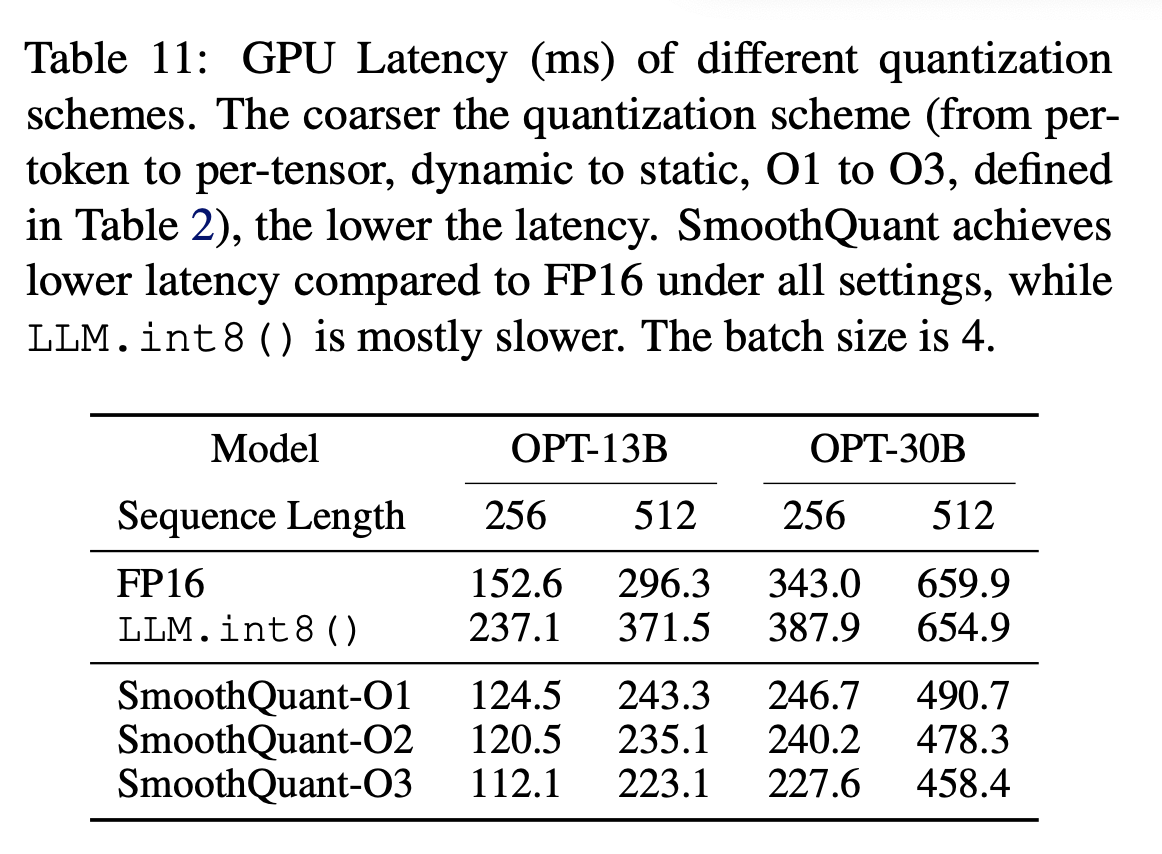
Quantization Schemes(O1 ~ O3)

static quantization이 확실히 inference를 가속화 할 수 있다

Migration strength ($\alpha$)

서로 다른 $\alpha$의 효과에 대한 ablation study 진행: OPT-175B with LAMBADA

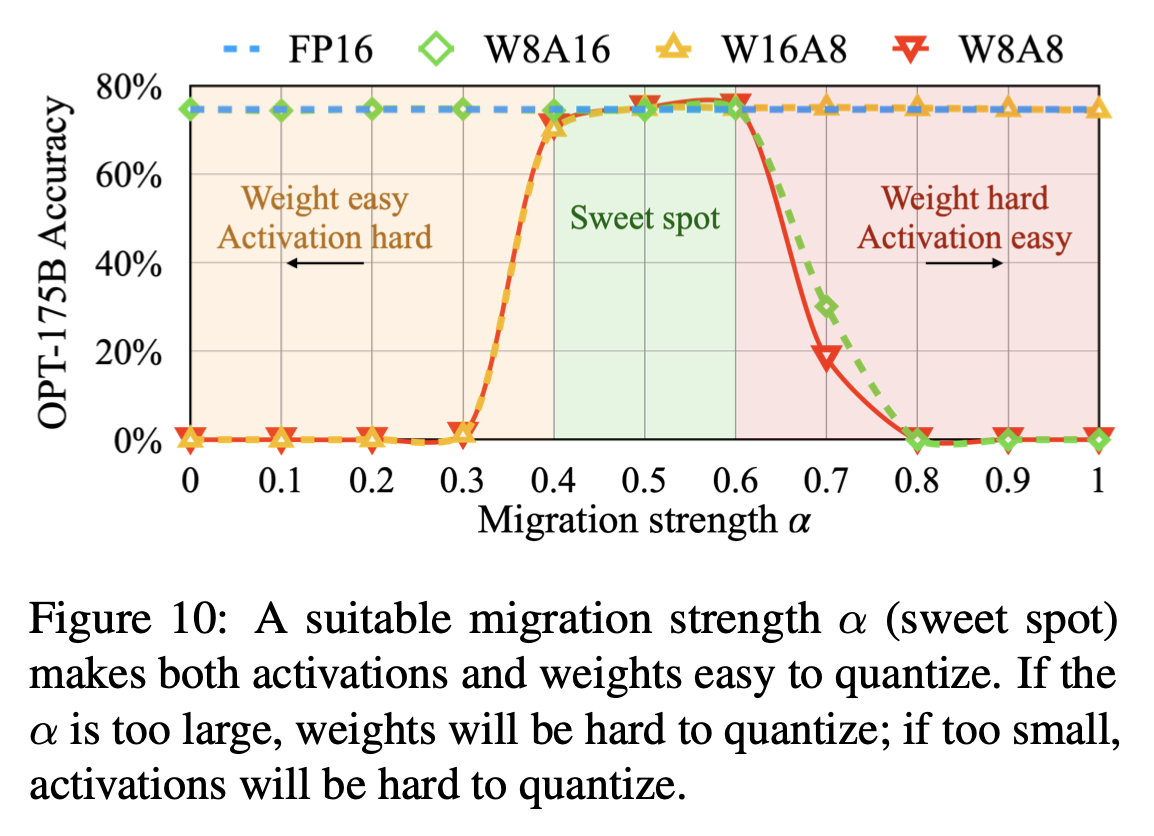
• $\alpha < 0.4$ : activation을 quantization 하기 힘듦
• $0.4 \leq \alpha \leq 0.6$ : sweet spot region
• $0.6 < \alpha$ : Weight를 quantization 하기 힘듦

---

느낀점

Quantization Loss를 줄이기 위해서는 Quantization 하는 부분의 이상치를 어떻게 컨트롤 해주는지가 중요하다는 것을 느꼈다.

어디서 이상치가 발생하고, 어떤 패턴으로 이상치가 발생하는지.. 그리고 이러한 이상치를 어떻게 해결할 수 있을지에 대한 연구가 quantization 방법론 연구 및 발전에서 주안점 인 것 같다(내 개인적인 생각)