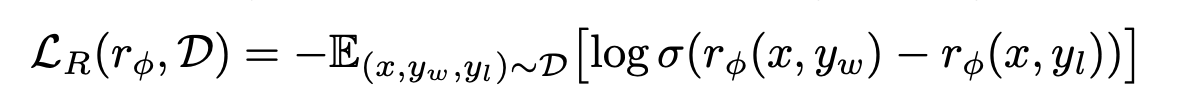Paper review[Direct Preference Optimization: Your Language Model is Secretly a Reward Model]

이상민·2024년 11월 23일

Paper

논문리뷰

목록 보기

19/29

paper: https://arxiv.org/pdf/2305.18290

도입)

매우 넓은 지식과 능력으로부터 모델의 원하는 답변들과 행동들을 선택하는 것은 안전하고, 성능이 좋고, 제어 가능한 AI system을 만드는데 중요하다.

배경)

기존에는 Human Preference를 학습시키기 위해 RL 알고리즘을 사용했다. 하지만 이 방법은 너무 복잡하다 & 종종 불안전한 절차

의의)

RL을 사용하지 않고 간단한 binary cross-entropy objective를 사용해서 human preference를 학습시킬 수 있다. 기존의 RLHF와 같은 목표를 최적화하지만, 구현 & 학습은 간단한 DPO.

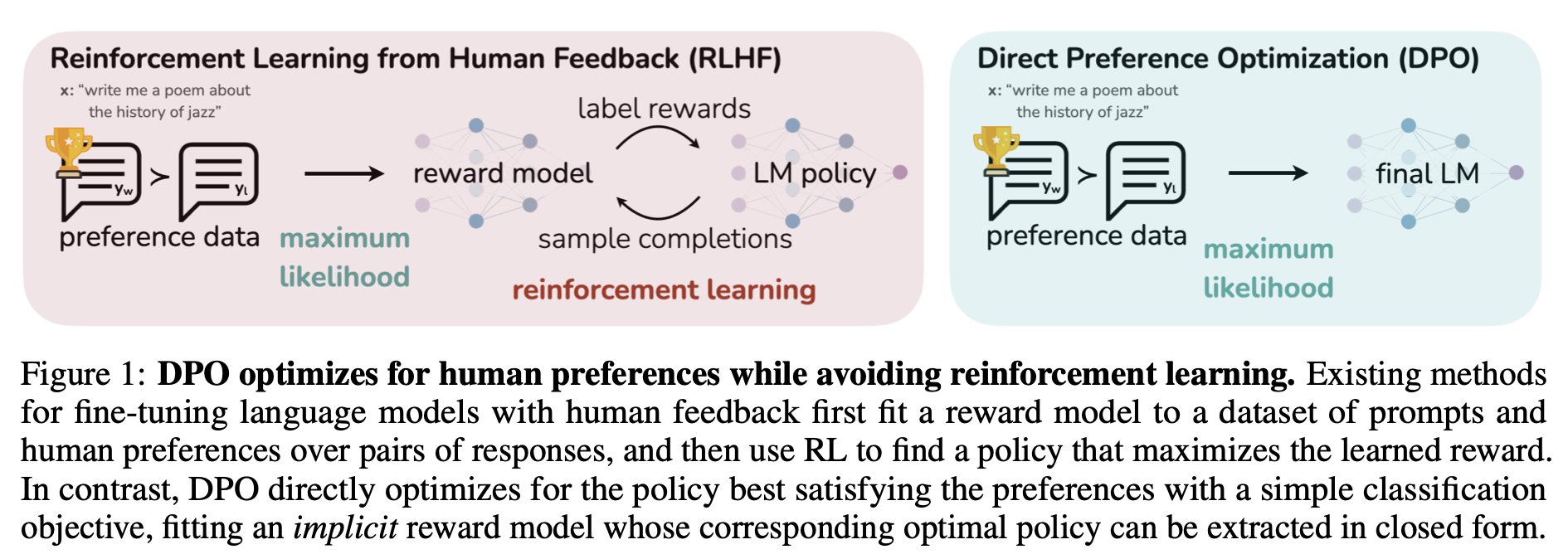
<그림: 기존 RLHF vs DPO>

요약)

Reward model parameterization의 특정 선택을 통해서 강화 학습 훈련 루프 없이 최적의 선택을 한 번에 추출할 수 있도록. 닫힌 상태로! → 반복적인 계산이 필요 없음. 강화 학습의 복잡한 루프를 반복할 필요 없이, 효율적으로 최적의 행동 정책을 얻을 수 있는 장점

Preliminaries: RLHF)

RLHF는 3가지 단계 존재:

SFT(Supervised Fine-tuning)
Preference sampling and reward learning
RL optimization

1. SFT

우리가 할 task에 맞게 pretrained LM finetuning → $\pi^{\text{SFT}}$

2. Reward Model Phase

$\pi^{\text{SFT}}$ 가 prompt $x$ 를 입력으로 넣고 2개의 responses 생성
Human Labeler가 responses를 보고, preference를 넣음 → $y_w$ : preferred completion, $y_l$ : dispreferred completion (표기: $y_w \succ y_l \,\,\, | \,\,\, x$ )
Preferences는 우리가 접근할 수 없는 일부 latent reward model에 의해 생성: $r^* (y, x)$
Model preferences를 사용하는 approach들이 많지만, Bradley-Terry(BT) model 사용 (유명하기에)
BT model의 human preferences distribution $p^*$ :

p^*(y_1 \succ y_2 |x) = \frac{\exp(r^*(x, y_1))}{\exp(r^*(x, y_1)) + \exp(r^*(x, y_2))}

$p^*$ 에서 샘플링된 Static dataset $\mathcal{D} = \{x^{(i)}, y^{(i)}_w, y^{(i)}_l\}_{i=1}^N$ 에 access한다고 가정하면, reward model( $r_\phi(x,y)$ )을 parameterize 할 수 있고 maximum likelihood를 통해서 parameters를 추정할 수 있다. 문제를 이진 분류(binary-classification)으로 구성하면 negative log-likelihood loss를 가질 수 있음:

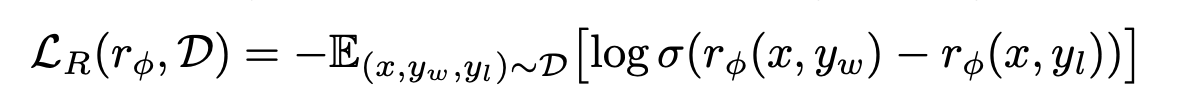
쉽게 생각하면, “human preference data를 사용해서 reward model 추정(학습)“

여기서 preference는 human labeler가 선택함(두 response 중에 무엇이 더 좋은지) & 그러나 rating은 다른 reward model을 통해 함
BT model을 사용해서 human preference distribution $p^*$ 만들기
Distribution을 사용해서 reward model 추정(학습)

3. RL Fine-Tuning phase

학습된 Reward model을 사용해서 LM에게 feedback을 주고, “LM optimizing”

\max_{\pi_{\theta}} \mathbb{E}_{x\sim \mathcal{D}, y \sim \pi_{\theta}(y|x)}[r_{\phi}(x, y)] - \beta \mathbb{D}_{\text{KL}}[\pi_{\theta}(y|x) || \pi_{\text{ref}}(y|x)]

최적화 방향: “Reward는 최대화” + “기존 모델과의 KL div는 최소화”

KL div를 통해 기존의 LLM과 큰 차이를 만들지 않으려고 하는 이유:

LM은 이미 잘 학습되어있다. 여기서 human preference를 추가하는 것이므로 모델을 너무 크게 변화시키면 좋지 않다
(크게 변화시키면 이전에 잘 작동하던 동작들과 많이 달라질 수 있음 → 불안정성 증가)
기존의 모델에서 많이 벗어난 행동들은 좋지 않은 행동일 확률이 큼
→ 이미 pretraining, finetuning에서 비효율적으로 판단된 행동 or 환경에서 잘 관찰되지 않는 행동

DPO 방법)

DPO objective 도출 (LM optimizing)

\pi_r(y|x) = \frac{1}{Z(x)}\pi_{\text{ref}}(y|x) \exp \left(\frac{1}{\beta}r(x,y)\right)

여기서 $Z(x) = \sum_y \pi_{\text{ref}}(y|x) \exp \left(\frac{1}{\beta} r(x,y)\right)$

도출 설명)

위의 RLHF의 RL fine-tuning phase의 LM optimizing objective

위에 대한 추가 설명(자세한 이해):
RL fine-tuning phase에서의 optimize objective과 같다.

1 → 2 식 : KL divergence의 식을 이용한 것! 아래의 식을 이용한 것! $KL(Q || P) = \sum Q \log \frac{Q}{P} = \mathbb{E}_{x \sim Q}[\frac{Q}{P}]$

2 → 3 식 : 목표가 $\pi$ 를 optimize 하는 것이기에, $-\beta$ 를 빼주며 max → min 으로 변경해도 괜찮음

3 → 4 식:
$Z(x)$ 를 더했다가 빼주는 이유: log의 아래항인 $\pi^{\star}(y|x)$ 를 확률 분포로 만들기 위해서 partition function을 나눠준다.
그래야 $\sum \pi^{\star}(y|x) = 1$ 이 되며, 확률 분포가 될 수 있다! 그렇기에 partition function을 나눠준다.

Partition function은 $\pi$ 에 관련되어 있지 않다 → 그래서 log 밑 부분을 다음과 같이 치환할 수 있다:

\pi^* (y|x)=\frac{1}{Z(x)}\pi_{\text{ref}}(y|x)\exp \left(\frac{1}{\beta}r(x,y)\right)

$\pi^*$ : valid probability distributioin $(\because \pi^*(y|x) \geq 0 ,\forall y \quad \& \quad \sum_y \pi^*(y|x) = 1)$

\therefore \min_{\pi} \mathbb{E}_{x \sim \mathcal{D}}[\mathbb{E}_{y \sim \pi(y|x)}[\log \frac{\pi(y|x)}{\pi^*(y|x)}]-\log Z(x)] =\\ \min_{\pi} \mathbb{E}_{x \sim \mathcal{D}}[\mathbb{D}_{\text{KL}}(\pi(y|x) \parallel \pi^*(y|x))-\log Z(x)]

$\pi$ 를 이용해서 해당 값을 minimizing 하는 것 → $Z(x)$ 는 $\pi$ 와 관계가 없으니, KL div를 통해서 최소값!

즉, $\pi(y|x) = \pi^*(y|x) \rightarrow \pi(y|x) = \pi^* (y|x)=\frac{1}{Z(x)}\pi_{\text{ref}}(y|x)\exp \left(\frac{1}{\beta}r(x,y)\right)$

따라서

r(x,y) = \beta \frac{\pi_r(y|x)}{\pi_{\text{ref}}(y|x)} + \beta \log Z(x)

이 식의 의의: 'reward model'을 대체할 수 있다!

Ground-truth reward $r^*$ 와 그에 해당하는 optimal model $\pi^*$ 에 위의 reparameterization을 적용할 수 있음(RLHF의 BT model human preference distribution에 위의 식 넣은 것)

p^*(y_1 \succ y_2 |x) = \frac{\exp(r^*(x, y_1))}{\exp(r^*(x, y_1)) + \exp(r^*(x, y_2))} = \frac{1}{1 + \frac{\exp(r^*(x, y_2))}{\exp (r^*(x, y_1))}}\\ = \frac{1}{1+\exp(r^*(x, y_2) - r^*(x, y_1))}= \frac{1}{1 + \exp (\beta \log \frac{\pi^*(y_2|x)}{\pi_{\text{ref}}(y_2|x)} - \beta \log \frac{\pi^*(y_1|x)}{\pi_{\text{ref}}(y_1|x)})}

Human preference data의 확률을 reward model 대신에 optimal policy를 통해서 표현할 수 있음 → $\pi_\theta$ 에 대한 maximum likelihood objective를 공식화 할 수 있다(위의 reward modeling과 유사):

\mathcal{L}_{\text{DPO}}(\pi_\theta ; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{\pi_\theta(y_w|x)}{\pi_{\text{ref}}(y_w|x)} - \beta \log \frac{\pi_\theta(y_l|x)}{\pi_{\text{ref}}(y_l|x)}\right)\right]

의문점) 왜 최종 $\mathcal{L}_{\text{DPO}}$ 가 Reward 함수의 Loss와 유사한가?

$\pi$ 최적화: Reward ↑ + $D_{KL}$ ↓

기존 RLHF) Reward model 추정 → $\pi$ 최적화: Reward ↑ + $D_{KL}$ ↓

DPO) $\pi$ 최적화: Reward ↑ + $D_{KL}$ ↓ (동일)

우선 reward는 $\pi$ 와 관계가 없으므로 $D_{KL}$ 최소화를 통해 $\pi$ 최적화
그렇게 $\pi$ 를 최적화 하면, 보상 함수에 대한 식이 생성됨 ( $r(x,y) = \beta \frac{\pi_r(y|x)}{\pi_{\text{ref}}(y|x)} + \beta \log Z(x)$ )
그러면 보상 함수는 $\pi$ 를 통해 최적화 할 수 있음 → 보상 함수의 Loss를 통해 최적화
기존 보상 함수 Loss에 위에 구한 식을 넣어보자:

\mathcal{L}_R(r_\phi, \mathcal{D}) = -\mathbb{E}_{(x,y_w,y_l) \sim \mathcal{D}}[\log \sigma(r_\phi(x, y_w) - r_\phi(x,y_l))] \\ \rightarrow \mathcal{L}_{\text{DPO}}(\pi_\theta ; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}}\left[\log \sigma \left(\beta \log \frac{\pi_\theta(y_w|x)}{\pi_{\text{ref}}(y_w|x)} - \beta \log \frac{\pi_\theta(y_l|x)}{\pi_{\text{ref}}(y_l|x)}\right)\right]

최종적으로 말하면, reward modeling에 KL-div 최적화가 들어가 있는 모습!

느낀점

이전에 한 번 보고 정리해 놓은 논문이었다.
다시 보는데, 이해가 갑자기 막힌 부분이 있었다.
기록을 항상 잘해놓아야 할 것 같다.

또한 기록을 잘 해놓으며, 리마인드 할 때 기록을 잘 봐야할 것 같다(왜냐하면 이번에는 설명해놓은 것을 안보고 혼자 다시 이해하려다가 시간이 꽤나 걸렸다..)

"의문점이라고 해놓은 부분에 대해서•••"
의문점이라고 해놓은 부분은 처음 볼 때, 'reward modeling에 사용한 Loss에 새롭게 도출된 r(x,y)를 넣어주었구나!' 라고만 생각하고 넘어갔었다.
다시 논문을 이해할 때(지금)는 '왜 그게 최종 정책 최적화 공식이 되는거지?' 라는 의문이 생겨서 이에 대해 고민하고 추가한 부분이다.
최종적으로는 이해했다.

식들이 대체되는 부분에서 '당연하다'라고 생각하지 않고, '왜 식들이 대체되는지에 대한 이유'를 생각해야 한다!

이상민

수학, AI, CS study 그리고 일상🤗

이전 포스트

Paper review[Efficient Large Language Models: A Survey]

다음 포스트

Paper review[Direct Preference Optimization: Your Language Model is Secretly a Reward Model]

논문리뷰

도입)

배경)

의의)

요약)