url: https://arxiv.org/abs/2112.04426
배경)
언어 모델의 크기가 커짐 → 다양한 task에서 모델의 성능이 좋아짐
이에 따라오는 비용들
- 추가적인 계산양
- 증가된 학습 데이터 메모리
따라서 계산양을 크게 늘리지 않고, 대규모 메모리로 모델을 효율적으로 증강할 방법을 연구
→ 언어 모델 scaling 대신, 큰 text database에서의 retrieval 제안
의의)
- RETRO: Retrieval-Enhanced Autoregressive Language Model 제안
- Retrieved text를 통합하기 위해 Chunked Cross-Attention module 사용 → Retrieved text에 linear한 time-complexity가 사용됨
- Pretrained Bert Model을 사용 → retriever network를 학습하고 업데이트 해야 하는 필요성 제거
- Model size & Database size scaling
- 150M ~ 7B 모델에 일정한 이득 제공
- Database size 증가 & Retrieved nighbors 증가 → Evaluation time에서 개선
- TEST SET LEAKAGE 문제 해결을 위해 “an evaluation aware of proximity of test documents with the training set” 제안
- Test set leakage이란? test data와 training data에 중복되거나 관련된 정보가 존재하여, test 데이터를 이미 학습했을 가능성을 열어두어 평가의 공정성 & 일반화 성능 손상
방법)
입력 시퀀스를 청크 단위로 찢어서, 이전 청크와 비슷한 텍스트를 retrieve 해와서 현재 청크 예측을 향상시킴
Retrieval database size 증강: billions of tokens → trillions of tokens
Retrieve 단위: 연속된 청크 단위 O, 개별 token X → 저장 & 계산 요구를 큰 선형 비율로 낮춤
Key-Value databases 생성
- Value: text token의 raw chunks를 저장
- Key: Frozen Bert Embeddings
Frozen model 이용 → 학습 동안 전체 database에 대해 embedding을 재계산하지 않게 함
각 학습 문장은 청크 단위로 찢어짐 → Database로부터 KNN을 통해 증강됨
Training Dataset
- 사용한 데이터셋(학습 & Retrieval): MassiveText의 multi-lingual version → 5 trillion tokens로 구성됨(아래표)
- 시퀀스는 학습 데이터의 subset에서 sampling. 아래 표의 sampling frequency가 sampling weight
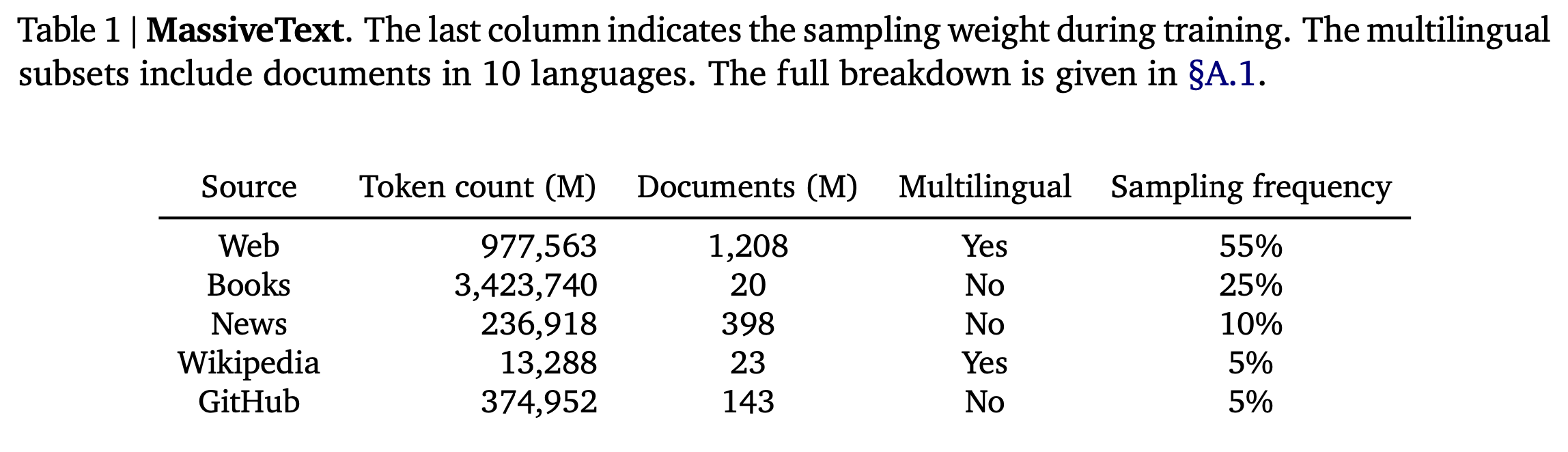
- 128,000개 토큰의 Vocabulary를 가지고 SentencePiece를 사용해 Dataset tokenizing
- 학습 동안 학습 데이터에서 600B tokens를 retrieve(별도로 명시되어 있지 않은 한). 아래 테이블의 weight로 sampling
- Training Retrieval Dataset도 training data와 같은 subset을 사용. 그리고 training 학습 frequency와 동일한 비율
- Evaluation 동안: Retrieval database는 full union of these database로 구성(Books만 4%의 sub-sample 이용) → Evaluation Retrieval Database: 1.75T
- Test Set Leakage 방지를 위해!
- train doc과 test doc의 13-gram Jaccard similarity가 0.8 이상인 모든 training documents를 validation or test set document에서 제거
- Text, Validation set은 Wikipedia 학습 dataset의 Wikitext103에서부터 온 article 제거
Retrieval-enhanced autoregressive token models
‘요약: 청크 단위로 database 구성 & chunk를 retrieval 해와서 사용’
n-token-long example을 l개 chunk의 sequence로 split!
Token : 내의 정수(tokenizing; token index)
. 여기서 청크 사이즈: . 즉,
여기서 : 내의 정수(token index)
각각의 chunk 를 database 로부터 k개의 neighbor인 집합으로 증강.
여기서, 는 non-trainable operator
Token likelihood: input(previous + retrieved neighbors)을 입력으로 받았을 때, 모델이 제공(로 parameterized 된 모델)
Retrieval-enhanced sequence log-likelihood:
: log probability
해당 식에서 알 수 있듯이, likelihood는 autoregressivity를 보존 ⇒ 현재 예측 토큰의 ‘이전 토큰들()’과 ‘이전 청크들로부터 retrieved된 데이터()’를 기반으로 현재 토큰 예측
Nearest neighbour retrieval
-
Dataset은 Key-Value memory로 구성
- Value: 2개의 contiguous chunks [N, F]
- N: Neighbor chunk ⇒ key 계산에 사용됨
- F: Original document 내에서의 continuation (동일한 문서 내에서 청크 N 이후 연속적으로 나오는 chunk)
- Key: Bert Embedding of 𝑁, averaged over time. Bert(N)이라고 표시 → 청크는 여러 개의 토큰으로 구성된다. 그렇기에 ‘평균화 된 N’이라는 것은 청크 내 각 토큰 embedding의 평균을 의미하는 것 같다.
- Value: 2개의 contiguous chunks [N, F]
-
각 chunk C에 대해, bert embedding에 대한 거리를 사용해서 key-value database로부터 근사 KNN을 retrieve ⇒ 모델이 얻는 값:
- Neighbour(N) & neighbour의 continuation(F)의 사용은 의미있는 개선을 보임
-
에 대해 길이 64를 사용 → 는 의 shape을 가짐 (여기서 r=128. 64 x 2)
-
SCaNN library를 통해 approximate nearest neighbours를 시간 안에 query 할 수 있음 (T elements의 database에 대해) → 2 trillion token database를 10ms 안에
-
이 에 들어가지 않게 하기 위해(causality 유지를 위해), 학습 시퀀스(X)와 같은 document에서 나온 neighbours를 필터링한다
- 이 부분에서 의문점)
- Retrieval neighbour set이 학습 시퀀스의 미래 청크를 가지면 안되는 이유를 이해하지 못하겠다.
- 의문의 이유)
- 현재 상태: retriever는 학습이 되지 않는 frozen 상태
- 미래에 나올 수 있는 청크를 retrieve 해온거면, retriever가 잘 retrieve 해온 것이 아닐까? 이를 활용하면 다음 청크 내의 토큰들 예측이 쉬워질 것이니까
- RAG의 목적)
- input에 대한 답을 내릴 때, 참고할만한 정보를 input에 보강해주며 답변에 도움을 주는 방법
- e.g.) ‘크리스마스가 뭐야?’ 라는 query에 대해 ‘크리스마스에 대한 wikipedia 정보’를 query에 보강해줘 모델에 입력하는 방식
- 근데 여기서 크리스마스에 대한 wikipedia를 사용하지 못하게 만드는 느낌이라.. 이해가 안되었다.
- 여기서 발생할 수 있는 문제는 2가지로 보인다:
- 계속해서 미래 청크를 retrieve 해오는 형태로 retriever가 학습되는 문제 → retriever는 frozen 상태라서 문제 안됨
- Test에서는 query에 대해 정확히 참고할 document가 database에 없는 경우에 대한 성능 하락
- 학습 과정에서 미래 청크를 retrieve 해와 neighbour chunk로 사용하는 경우가 많아지면, language modeling에서 neighbour chunk를 간접적으로 사용하는 것이 아니라 직접적으로 사용하도록 학습이 진행될 수 있음
- 그러나 Test query와 직접적 연관이 있는 document가 database에 없다면, 해당 query의 답변에 대한 미래 청크 또는 직접 관련이 있는 청크들을 retrieval 할 수 없다 → 그 상황에서 retrieved neighbour chunk를 language modeling에 직접적으로 사용한다면 성능 악화를 일으킬 수 있다.
- 내가 이해한 바)
- 최대한 원래 document의 도움 없이 language modeling을 학습할 수 있게 하기 위해 이러한 장치를 넣은 것 같다.
- 이 부분에서 의문점)
RETRO model architecture
- Encoder-Decoder 구조 & cross-attention 메커니즘을 통해 retrieved data 통합
- Transformer decoder에서 “Retro-blocks” & “standard Transformer blocks” 결합
- Decoder는 Retro-block과 standard Transformer blocks를 번갈아가며 사용
- Retro-blocks : retrieved data와 현재 상태인 H를 결합하여 retrieval된 정보를 디코더에 통합
- Standard Transformer blocks : 일반적인 transformer 구조로 주어진 입력에 따라 다음 토큰을 생성
- Hyperparameter P를 이용하여 Retro-block이 적용될 layer를 결정. ex)
- 상세 식)
-
FFW: Fully-connected layer
-
ATTN: standard sequence-level self-attention layer
-
CCA: chunked cross-attention layer
위 3가지 식들은 모두 autoregressive operator: i번째 output은 반드시 을 기반으로 생성
-
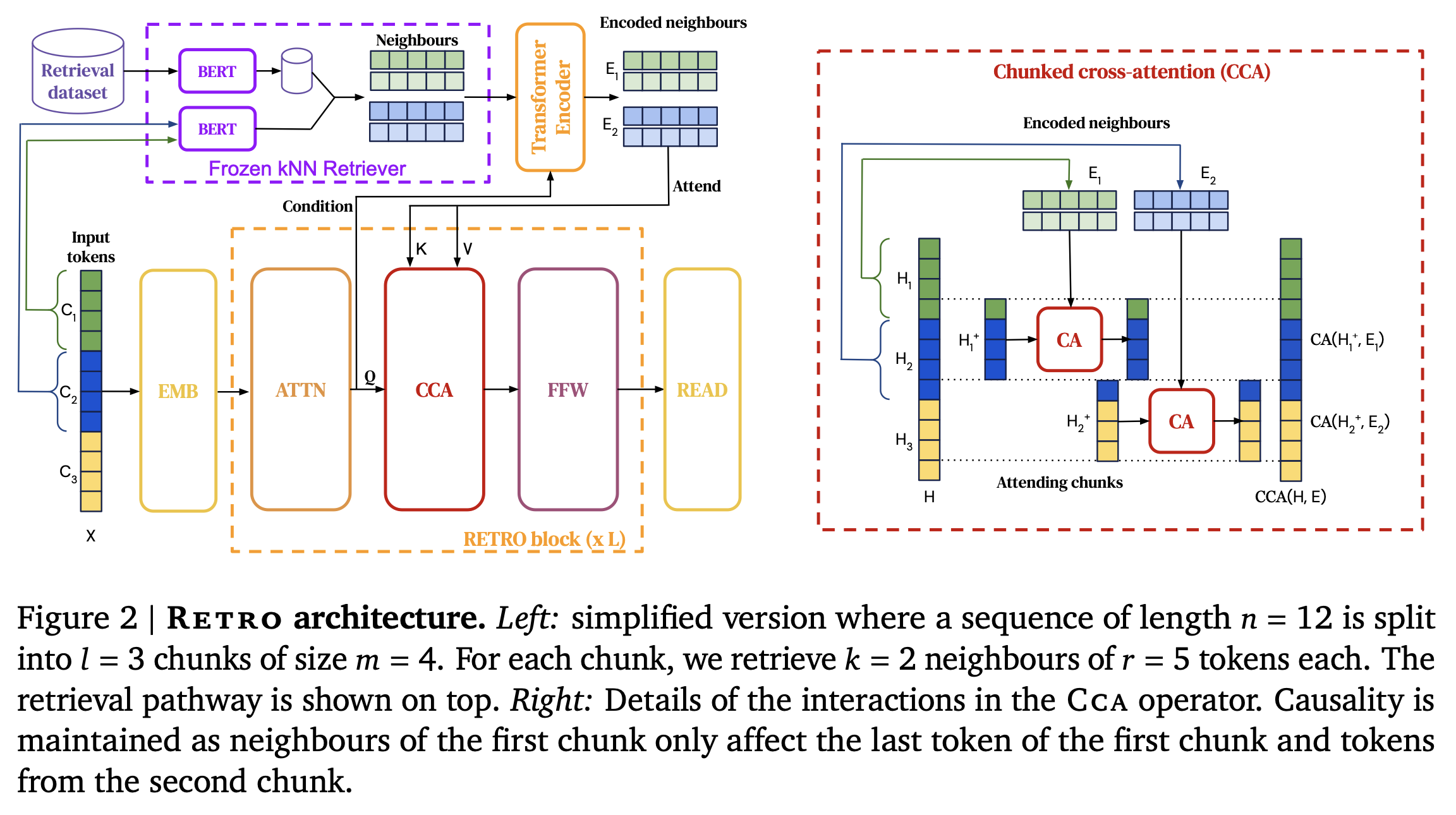
<RETRO architecture>
Encoding Retrieval Neighbours & 알고리즘
Standard Transformer blocks에서는 Retrieved Chunk Encoding이 필요 없음( 이니까 )
그러나 RETRO block에서는 Retrieved Chunk의 Encoding이 필요함(chunk encoding);
Encoding 방법) Encoder 부분이라고 부름(chunk 내 attention이 bi-directional이라)
- 먼저 u번째 chunk의 j번째 neighbour를 encoder를 통해서 embedding 형태로 만듦: (청크 내 토큰의 수 x hidden dimension)
- 그 후 encoder의 layer를 타고 올라가며 encoding 진행
- Chunk 내 token끼리 bi-directional attention(self-attention): [Retrieved 청크 내 토큰들 간 정보 교환]
- (조건부) 만약 에 속하는 layer면, 와 정보 교환을 진행하여 Encoding update: [retrieved chunk encoding에 현재 청크 정보 추가]
- Fully-connected layer 통과
: cross-attention이 진행될 layer의 index 집합
모든 청크에 대한 모든 neighbours는 병렬적으로 인코딩 됨 ⇒ 전체 인코딩 집합: . Chunk 에 대해 인코딩 된 neighbours:
전체 알고리즘) Decoder 부분이라고 부름(H 내 attention이 causal attention이라)
Decoder의 layer를 타고 올라가며 진행
- 내 토큰 간 Causal attention 진행:
- [조건부] min(P) layer에서 Encoding 생성 (위의 방법을 통해: Encoding 방법)
- [조건부] 만약 에 속하는 layer면, CCA(Chunked Cross-Attention) 진행
- Fully-connected layer 통과
마지막 layer에서 토큰 예측
: cross-attention이 진행될 layer의 index 집합

[내가 이해하는 간단한 방법]
전체적 순서)
- Decoder에서 layer를 타고 올라간다
- 그러다 layer가 min(P)이면, ENCODING 만들기 start!
- Encoding 만들기 → Encoder의 layer를 1부터 타기 시작! → 그렇게 encoding 완료!
- 그렇게 완성된 encoding을 가지고 decoder에 계속해서 사용 & output 만들기
Encoder 알고리즘)
- layer마다 청크 내 token들끼리 self-attention
- 그러다가 P_enc의 layer에서는 ‘를 사용해 update를 추가’
- Fully-connected layer
을 통해 Retrieved chunks embedding 생성
전체 다시; decoder까지 설명)
- layer마다 H를 causal attention
- min(P) layer에서 Encoding 만들기 (이전 청크들의 Embedding 만들기)
- 만약 P의 layer에서는 CCA 하면서 H 만들기
- Fully-connected layer
- layer 마다 iteration 끝나면, READ(H)
Chunked cross-attention
- Intermediate activation 을 l-1개의 attending chunks로 나누기: ⇒ 위 architecture(Fig 2)의 오른쪽 부분에 묘사된 것처럼
- : ‘Chunk 안에서 last token & Chunk 안에서 앞의 m-1개 tokens’의 intermediary embeddings를 가짐
- 와 사이의 cross-attention 계산. ( : Chunk 로부터의 encoded retrieval set)
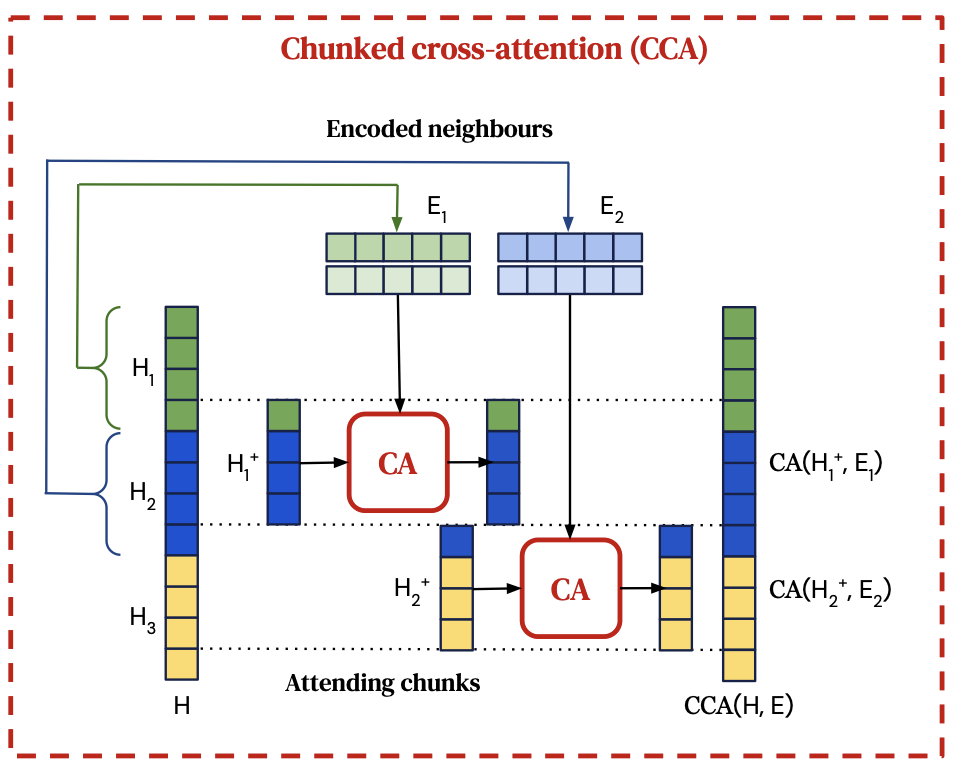
per-chunk cross-attention의 l-1개의 결과를 시간 순서대로 concatenate & 그리고 적절히 padding 처리
CCA의 output
각 chunk 와 각 토큰 에 대한 공식:
여기서 : time-concatenated encoded neighbours에 대한 cross-attention residual operator(3개의 parameter matrices 에 의한 간단한 버전)
모든 에 대해, (Y가 key-value, h가 query)
그러나 초기 m-1개의 토큰들은 이전 chunk의 neighbours를 attend 할 수 없다 → 그래서 이 위치에서는 를 identity로 정의:
CCA의 cross-attention이 이전 chunk의 neighbours( )만 attend 하지만, self-attention operation을 통해서 더 이전의 chunk neighbours의 내용도 전해질 수 있음 (CCA 전에 causal attention을 통해 이전 모든 neighbours에 대한 정보를 depend 할 수 있음)
⇒ 전체 이전 neighbours에 대해 quadratic cost가 들지 않은 채, u번째 청크의 i번째 토큰은 모든 이전 neighbours에 잠재적으로 depend 할 수 있음.
Sampling
- 원래 transformer에서 토큰 생성 비용: 생성 시퀀스 길이에 quadratic
- 추가된 Retrieval 비용: chunks의 수 에 linear
추가된 retrieval 비용은 무시할만하다(원래 토큰 생성 비용에 비해)
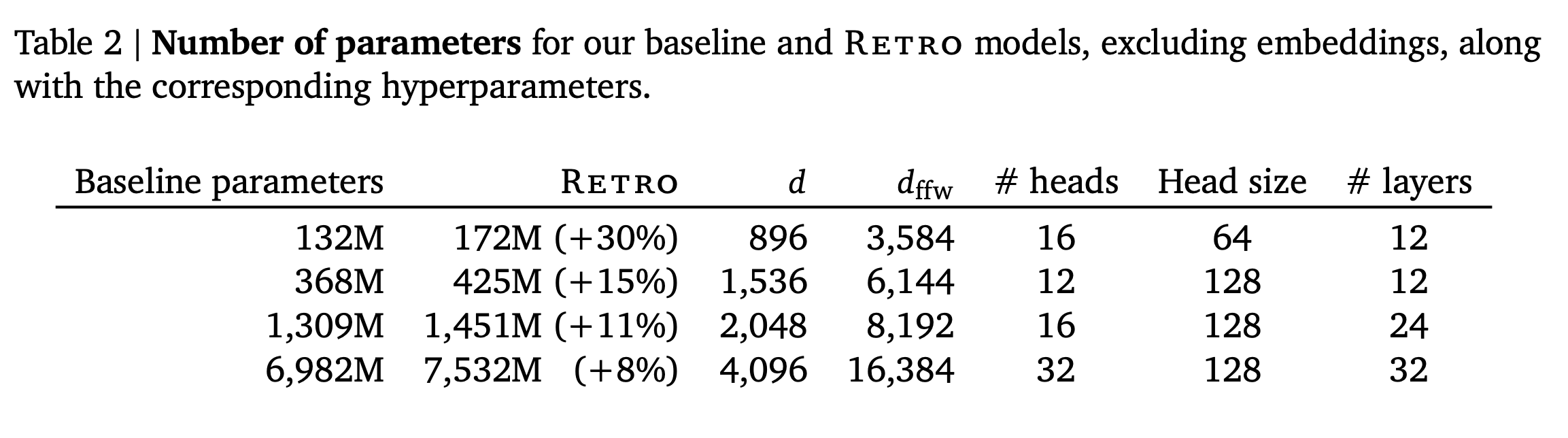
Baseline Transformer Architecture
기본 transformer architecture에서 약간의 변화:
- LayerNorm → RMSNorm
- Sinusoidal Encoding → Relative Position Encoding
Retrieval model은 3block 당 하나의 RETRO-block 포함
Quantifying dataset leakage exploitation
RETRO 방식의 경우, retrieval 메커니즘에서 평가 중 훈련 데이터와 겹치는 경우가 있을 수 있음
→ 모델이 이미 해당 데이터를 학습했기에, 평가시 이런 데이터가 사용된다면 성능이 뻥튀기 될 가능성이 있음
얼마나 "retrieval"이 language modeling 성능을 향상시켰는지 이해하기 위해(Retrieval 성능을 제대로 파악하기 위해서 ), evaluation likelihood 정량화.
→ 평가 데이터셋 & 학습 데이터셋의 overlap function 사용
학습 데이터와 평가 데이터의 중복 비율에 따른 성능 변화 측정 → retrieval이 language modeling 개선에 얼마나 영향을 줬는지 (그냥 학습 데이터셋 기억 효과에 불과하는지)
방법)
- Evaluation sequences 를 길이 의 chunk로 split → 학습 데이터를 chunk 집합 으로 본다
- 각 evaluation chunk 에 대해, 학습 데이터에서 가장 가까운 10개의 neighbours(길이 128까지)를 retrieve.
- Evaluation chunk와 neighbours에 공통적으로 사용되는 가장 긴 substring 계산 →
- → Evaluation chunk와 training data 간에 얼마나 overlap이 발생했는지 알 수 있음 (0: chunk가 안겹쳐졌을 때, 1: chunk가 전체적으로 보인 경우)
각 청크에 대한 log-likelihood & 인코딩 되는 bytes의 수 를 사용해서 성능 평가(bpb)
모델의 필터링 된 Bits-per-bytes를 고려할 수 있음(훈련 청크와 % 미만으로 겹치는 청크 집합의 bits-per-bytes 계산):
예측 성능에 대한 evaluation leakage impact를 평가할 수 있음 → 낮은 사용: 거의 새로운 청크에 대해서 모델의 성능 평가 가능
bpb는 0이상의 값이 나오며, 0에 가까울수록 좋음 (log-likelihood에 -를 곱해서 양수로 표현해주는 것 같음)
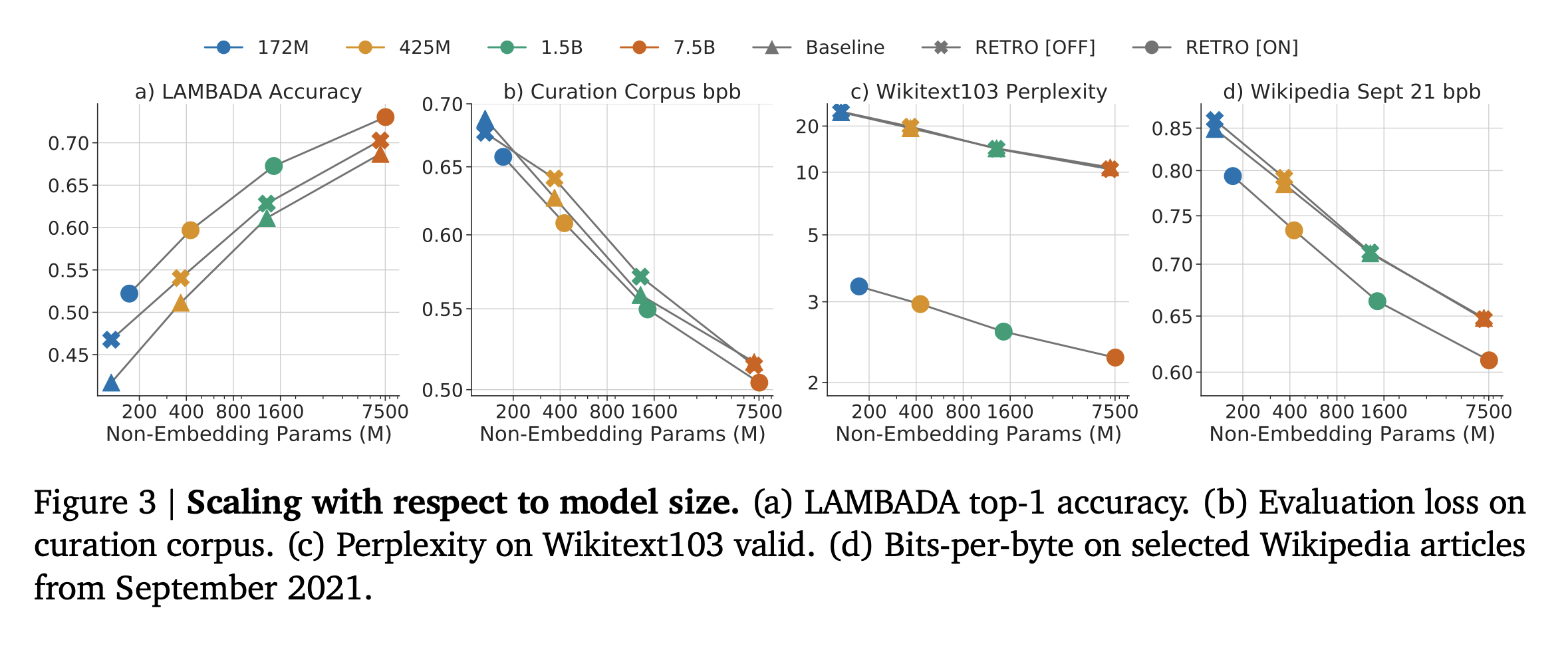
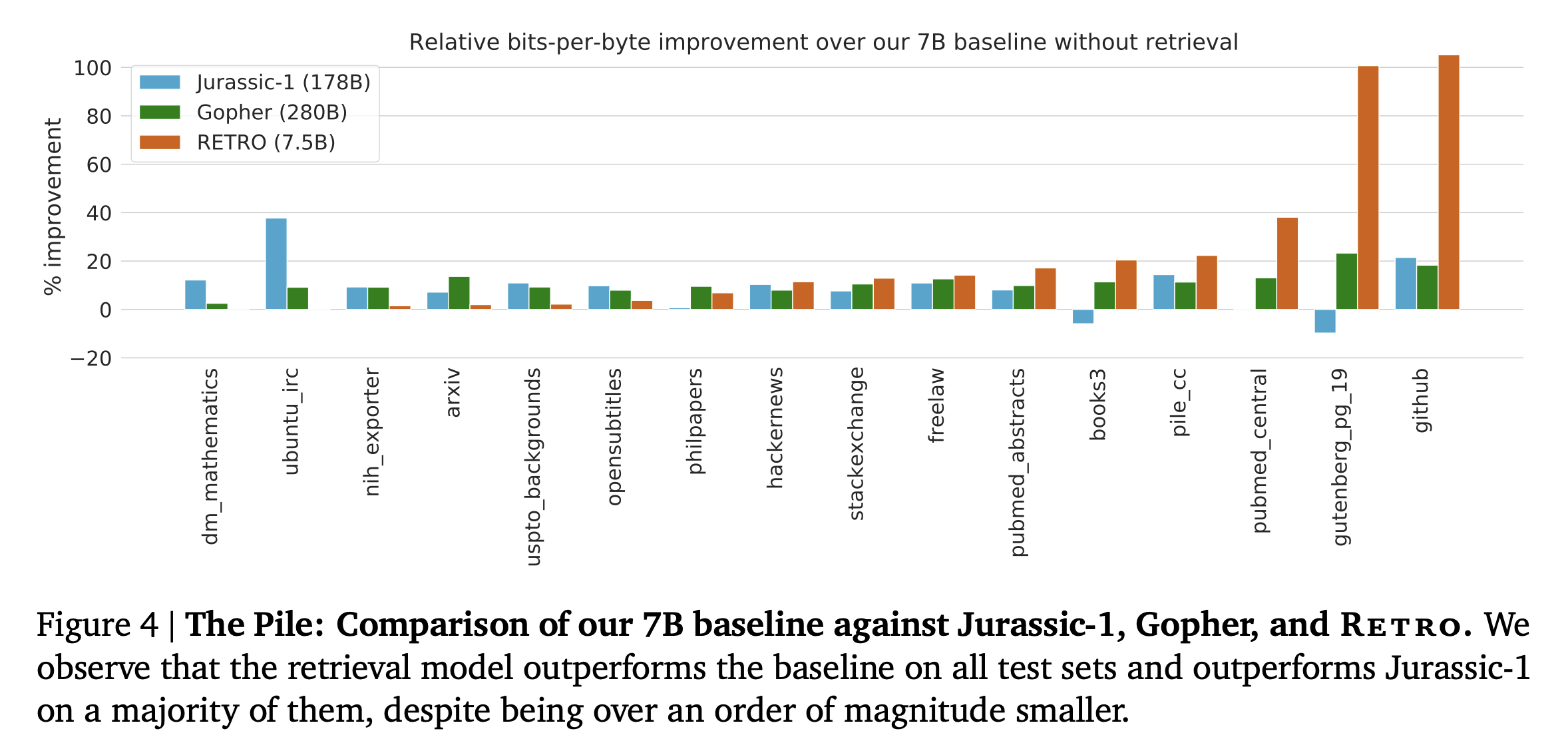
Results
Language modeling benchmark의 결과)
설명은 생략 & 몇몇 결과 Figure들..
느낀점)
논문을 다시 돌아봤을 때 느낀 의의)
- Chunk 단위로 retrieval database 구축
- 자원적으로 이득
- approximate nearest search를 통해 빠르게 search 가능
- 토큰 예측할 때, 이전 청크의 neighbours를 이용해서 retrieval augmented language modeling
- 현재 생성되는 청크의 바로 이전 청크의 Neighbours 청크들만 추가해서 계산하는 것이라 추가적인 계산은 무시할만함
- 하지만 CCA 전에 causal attention을 통해 이전 neighbours chunks들의 정보를 propagation 하여, 이전 모든 neighbours chunk에 대한 정보를 이용함
- 즉, 모든 neighbours chunk 정보를 사용하지만, 막상 계산은 이전 하나의 chunk에 대한 neighbours에 대해서만 계산이 진행됨
느낀점 & 의문점 & 궁금증)
- Retrieval 부분은 frozen 상태로 학습이 진행되지 않는다 → 괜찮은 Neighbours가 잘 retrieval 되어 오는지 확인할 필요가 없나? & 첫 bert의 성능이 매우 중요할 것 같다
- Chunk의 embedding을 chunk 내 토큰들의 bert embedding의 평균을 사용한다고 했는데, bert에 하나의 토큰을 넣어 해당 토큰의 Embedding을 뽑아 내고 각 토큰의 embedding을 평균 내는 것이 맞을까? → 청크 내 토큰들의 관계도 알 수 있게 하기 위해 전체 청크를 bert에 넣어 [CLS]를 가져와서 contextual 정보도 chunk embedding에 넣어주는게 좋지 않을까?
- Chunk embedding을 표현하기 위해 token embedding을 사용한다(token embedding의 평균). Token embedding을 구할 때 token 하나를 Bert에 넣어주어 embedding을 구하는데(), Bert architecture의 핵심은 attention 구조 아닌가? token이 하나 들어가면 self-attention의 이점이 제대로 작동하지 않는데, 왜 bert를 통해서 개별 token의 embedding을 구했는지 궁금하다
- Chunk 단위로 retrieval 해옴으로써 linear한 time-complexity가 걸리는 점이 인상 깊었다.
- Test data leakage에 대한 우려를 위해 r(C)라는 함수를 만들어, 특정 조건 하에서 retrieval의 성능을 평가한 부분이 좋았다(test data leakage 정도에 따른 retrieval 성능 평가)
