Paper review[DoRA: Weight-Decomposed Low-Rank Adaptation]

이상민·2025년 2월 28일

PEFT Paper

논문리뷰

목록 보기

29/29

url: https://arxiv.org/abs/2402.09353
code: https://github.com/NVlabs/DoRA

배경

LoRA가 추가적인 inference 비용이 없어서 좋지만, Full finetuning과 여전히 accuracy gap이 있음

의의

새로운 weight decomposition 분석: Full finetuning과 LoRA 사이의 고유의 차이점 연구
DoRA: LoRA와 비교했을 때, “학습 능력과 학습 안정성 개선 & 추가적인 Inference Overhead는 피함”
DoRA는 Full Finetuning과 유사한 학습 행동 → Full Finetuning과 매우 유사한 학습 능력

영감을 받은 아이디어
- “Weight Normalization”: weight reparameterization을 사용해 gradient의 conditioning 개선 → 빠른 수렴을 달성
Related works
- PEFT
  - Adapter-based methods
    - 설명: Frozen Backbone 안에 ‘학습시킬 module’을 넣어줌 → 학습 module은 크기가 작아서 학습시키는 parameters가 적어짐
    - 단점: 모델의 architecture를 변형시킨 것이라 inference latency 증가
  - Prompt-based methods:
    - 설명: 추가적인 soft tokens을 입력 앞에 넣어주고, 이들만 finetuning
    - 단점: 모델의 입력을 변형시킨 것이라 inference latency 증가
  - LoRA and its variants
    - 설명: low-rank matrices를 사용해서 학습 진행
    - 장점: 학습을 진행하고, low-rank matrices를 inference 전에 pretrained weight에 merge 시켜줘서 추가적인 inference latency가 발생하지 않음

Contributions

LoRA와 Full Finetuning의 pattern 분석

[LoRA]

Update 되는 matrix를 2개의 low-rank matrices의 곱으로 표현:

W' = W_0 + \Delta W \\\Delta W = B \times A, \quad W \in \R^{d \times k}, B \in R^{d \times r}, A \in \R^{r \times k}

$W_0$ 은 pre-trained weight로 finetuning동안 update 되지 않는다.
여기서 r은 d와 k보다 매우 작은 수이다 → 학습 파라미터 수를 줄인다.
A는 xavier uniform distribution & B는 0으로 initialization → $\Delta W$ 는 0으로 initialization
이렇게 학습된 $\Delta W$ 는 inference 시에, $W_0$ 에 merge 되어 사용된다 → 모델 architecture가 그대로 유지 → 추가적인 Inference latency 발생 X

[Weight Decomposition Analysis]

이전 연구들은 LoRA와 FT의 정확도 차이가 추가적인 분석 없이 ‘학습되는 parameter의 수 차이’ 때문이라고 여겼다(LoRA의 r을 키워주면, Full Finetuning과 유사한 수준의 표현력 얻을 수 있기에)

Weight matrix를 magnitude와 direction으로 reparameterizing 하여 optimization을 가속화하는 논문(Weight Normalization)에 영감을 받은 본 논문의 weight decomposition 분석 소개:

LoRA와 FT의 고유한 차이를 드러내기 위해 weight matrix를 두 가지 요소로 재구성 ⇒ “magnitude”, “direction”

Analysis Method
- 목표: LoRA와 FT에서의 magnitude와 directions의 update를 ‘Pre-trained weights’와 비교 → 학습 행동의 근본적인 차이 밝혀냄
- Weight Decomposition: $W = m\frac{V}{||V||}_c = ||V||_c \frac{W}{||W||_c}$ $m \in \R^{1 \times k}$ : magnitude vector, $V \in \R^{d \times k}$ : directional matrix, $||\cdot||_c$ : column에 대해 matrix의 vector-wise norm
- 본 논문 실험 디테일 & 실험 방법:
  - 사용한 모델: VL-BART
  - task: Four image-text tasks
  - LoRA 적용: query, value weight matrix
  - 실험 방법:
    1. Training steps 중 4가지 checkpoints 선택(3가지: intermediate steps, 1가지: final checkpoint)
    2. Pre-trained weight $W_0$ , Full fine-tuned weight $W_{FT}$ , merged LoRA weight $W_{\text{LoRA}}$ 를 weight decomposition (위의 weight decomposition처럼)
    3. ‘Pre-trained weight와 Full fine-tuned weight 비교(magnitude & direction 모두)’ & ‘Pre-trained weight와 merged LoRA weight 비교(magnitude & direction 모두)’
    4. FT와 Pre-trained 비교 식(각각 magnitude, Direction; LoRA도 이와 유사하게 계산):
      $\Delta M_{\text{FT}}^t = \frac{\sum_{n=1}^k |m_{\text{FT}}^{n, t} - m_0^n|}{k} \\ \Delta D_{\text{FT}}^t = \frac{\sum_{n=1}^k (1 - \cos (V_{\text{FT}}^{n,t} - W_0^n))}{k}$
Analysis Result
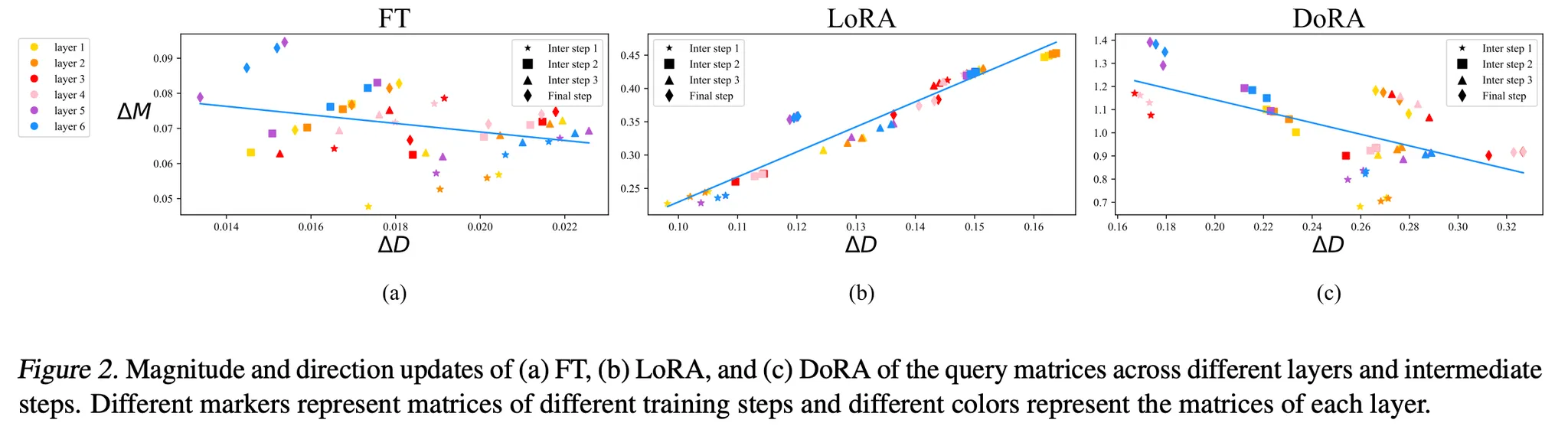
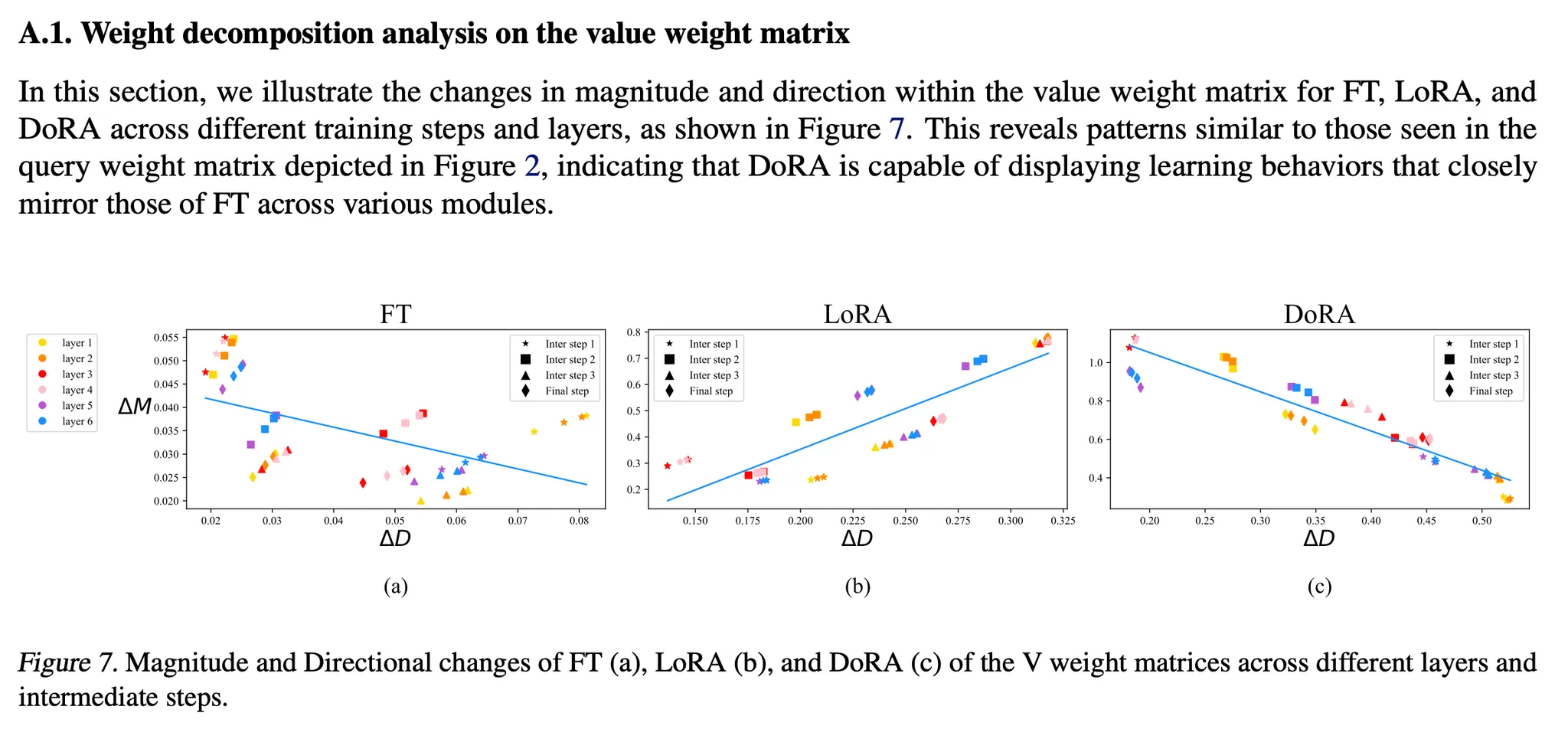
- 결과
  - LoRA: Magnitude & direction의 변화가 비례함 (양의 기울기 추세를 보임)
  - FT: LoRA보다 상대적으로 음의 기울기 추세를 가지며, 더 다양한 학습 패턴을 보여줌
- 분석
  - LoRA는 섬세한 조정 능력이 부족함: Magnitude와 Direction의 변화를 세밀하게 조정하기가 힘들다 → 한쪽만 세밀하게 조정하는 능력이 부족함 (Magnitude는 크게 조정하고, direction은 미세하게 조정하게 만드는 것이 힘들다(비례하는 경향이 있기에))
  - 반면 FT는 그렇지 않음 → 한 쪽의 섬세한 조정이 가능함
- 결론
  - 본 논문에서 FT와 유사한 학습 패턴을 가지며, LoRA보다 학습 능력을 향상시킬 수 있는 LoRA 변형을 제안

방법론

1. Weight-decomposed Low-Rank Adaptation

방법:

weight-decomposition을 함 → Direction, Magnitude 부분이 생김
Direction 부분은 LoRA를 사용해서 finetuning / Magnitude 부분은 그냥 finetuning

이유: 그냥 LoRA를 쓰면, direction과 magnitude의 변화가 양의 방향으로 진행되고 이는 Full Finetuning과 다른 양상을 띈다. LoRA와 FT의 학습 차이라고 보았고, direction과 magnitude를 따로 하되 direction은 parameter가 더 많으니까 direction에는 LoRA 적용

Intuition)

Magnitdue와 Direction을 다르게 학습
1. Magnitude: full finetuning
2. Direction : LoRA finetuning
결과: 학습 중, 두 부분 모두에 LoRA를 사용하는 것보다 하나에만 LoRA를 사용하는 것이 더 간단
Weight-decomposition을 통해 Direction update 부분 optimizing process가 더 안정적

[DoRA와 weight-normalization의 차이: 학습 approach]

Weight-normalization
- Scratch부터 학습 → Initialization이 학습에 민감함
DoRA
- Magnitude & Direction이 pre-trained weights로 시작 → Initialization 문제가 없음
- 식: $W' = \underline{m} \frac{V + \Delta V}{||V + \Delta V||_c} = \underline{m} \frac{W_0 + \underline{BA}}{||W_0 + \underline{BA}||_c} \quad \cdots \quad (5)$ $\underline{m}$ : magnitude(trainable), $V$ : frozen direction, $\Delta V$ : directional update이고, low-rank matrices $B, A$ 의 곱으로 표현(trainable) 여기서 $B, A$ 는 LoRA와 동일하게 초기화 → finetuning 전에 $W' = W_0$ 이 되게 하기 위해( $BA = 0$ )

[DoRA 결과 분석]

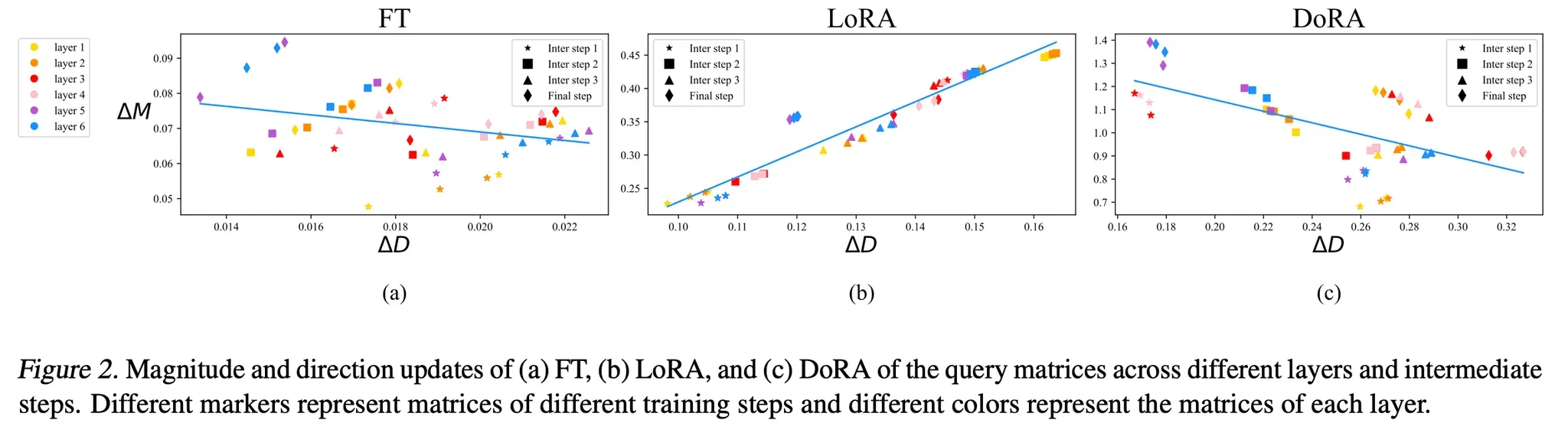
위의 Figure 2(analysis와 같은 figure)에서 $(\Delta D, \Delta M)$ 의 regression을 보면, DoRA와 FT는 유사한 패턴을 가지고 있고 LoRA와는 반대

FT가 이러한 negative slope을 가지고 있는 이유 추론)

Pre-trained weight는 이미 다양한 task에 맞는 상당한 정보를 가지고 있다 → Direction이나 Magnitude 둘 중 하나만 큰 변형을 하는 것이 downstream adaptation에 충분(둘 다 pretrained weight와 많이 달라질 필요 없다)

[ $\Delta D$ 와 $\Delta M$ 의 correlation 계산]

FT: -0.62
LoRA: 0.83
DoRA: -0.31

[결론]

DoRA는 FT와 유사한 “Direction에서 큰 변화 & Magnitude에서 작은 변화” 또는 “Direction에서 작은 변화 & Magnitude에서 큰 변화” 학습 패턴을 보이며, 이는 LoRA보다 우수한 학습 능력을 갖추고 있음을 보여준다

2. Gradient Analysis of DoRA

Loss $\mathcal{L}$ 의 gradient ( $m$ 과 $V' = V + \Delta V$ )

\nabla_{V'} \mathcal{L} = \frac{m}{||V'||_c}\left(I - \frac{V'V'^T}{||V'||^2_c}\right)\nabla_{W'} \mathcal{L} \quad \cdots \quad (6)\\ \nabla_m \mathcal{L} = \frac{\nabla_{W'}\mathcal{L}\cdot V'}{||V'||_c} \quad \cdots \quad (7)

식에 대한 설명은 생략하고, 결과적으로 표현

(6)의 식
- Weight Gradient( $\nabla_{W'} \mathcal{L}$ )에 대해서 $\frac{m}{||V'||_c}$ 은 scaling 부분, $I - \frac{V'V'^T}{||V'||^2_c}$ 은 projection 부분
- 이 두 부분이 gradient’s covariance matrix를 identity matrix와 가깝게 만들어 줌 → 최적화에 유리함
- 추가적으로 $\Delta_{V'} L = \Delta_{\Delta V} L \,\,(\,\,\because V' = V + \Delta V)$ → 그래서 위의 weight-decomposition에 따른 optimization 이점은 $\Delta V$ 에도 전해지고, 이는 LoRA의 학습 안정성을 향상시킨다
(7)의 식
- 식을 통해서 ‘direction에 대한 gradient가 크면, magnitude에 대한 gradient가 작아짐’ & ‘direction에 대한 gradient가 작으면, magnitude에 대한 gradient가 커짐’을 보였다.
- 이는 위의 figure 2의 (c)를 통해 실제와도 부합하다는 것을 보인다.
- 이러한 학습 패턴은 FT의 학습 패턴과 유사하다

3. Reduction of Training Overhead

$W$ 와 $\Delta W$ 의 gradient는 동일하다.

그러나 Eq (6)을 보면, DoRA는 low-rank adaptation을 directional component에 사용 → Low-rank의 update의 gradient는 $W'$ 의 gradient와는 다르다 → 이거 때문에 backpropagation 과정에서 extra memory overhead 발생

[해결 방법]
Equation 5에서 $|| V + \Delta V||_c$ 를 상수 취급해서 gradient graph에서 분리 → 티가 나는 정확도 차이 없이, gradient graph memory consumption을 매우 줄여줌

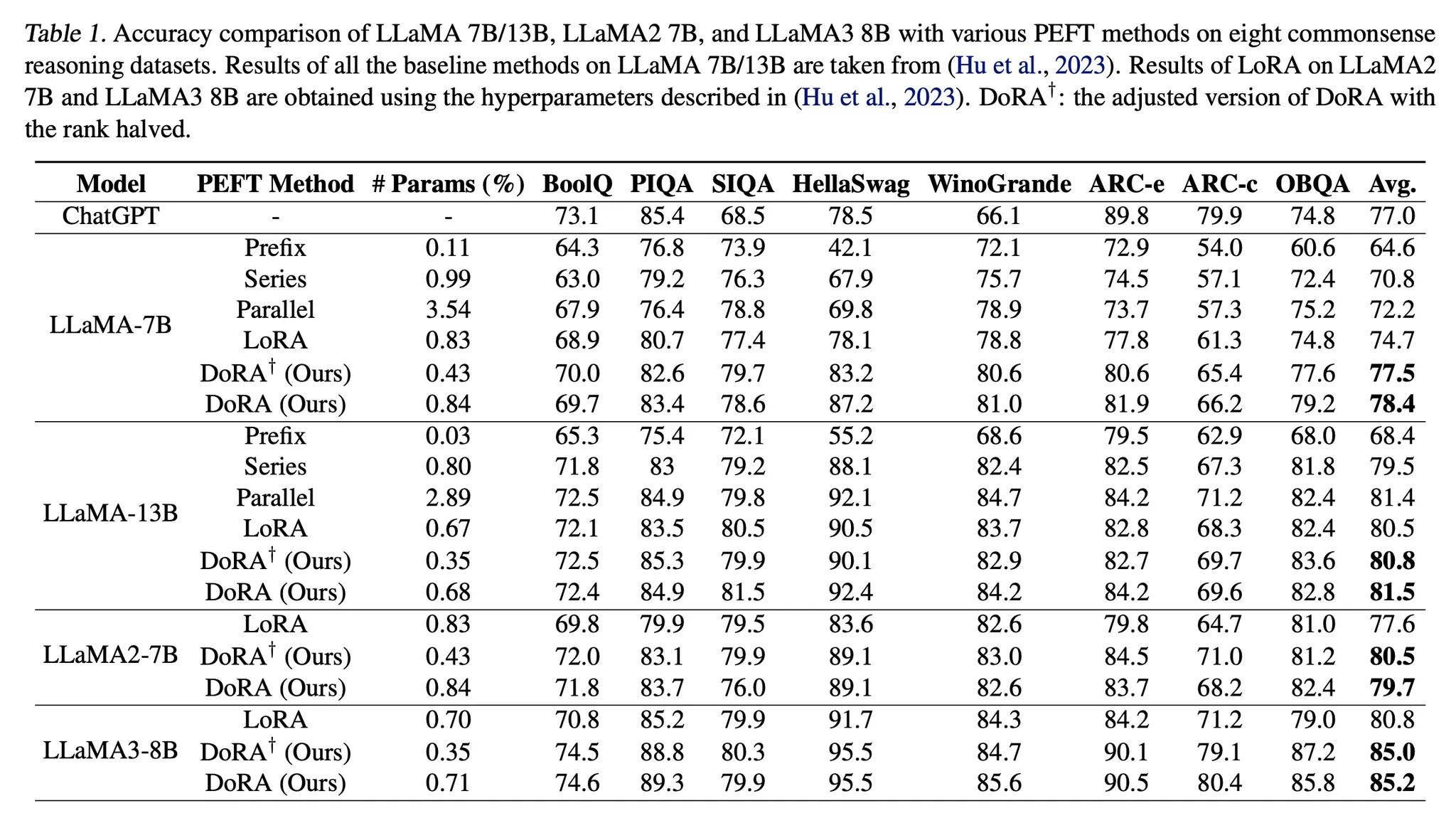
실험

Language, Image, Video 도메인에서 평가

나는 Language에 관심이 있으니까, language 실험 결과를 보도록 하겠다.

LoRA의 configuration을 유지 ⇒ rank(r)은 같게 유지하되, learning rate는 조정
학습 가능한 parameter가 LoRA보다 DoRA가 증가한 이유: 학습 가능한 magnitude component가 포함되었기 때문

[결과 테이블]

나의 생각)
- Parallel adapter 방법론과 series 방법론에 대한 이해를 돕기 위한 그림(출처: ”LLM-Adapters: An Adapter Family for Parameter-Efficient Fine-Tuning of Large Language Models”)
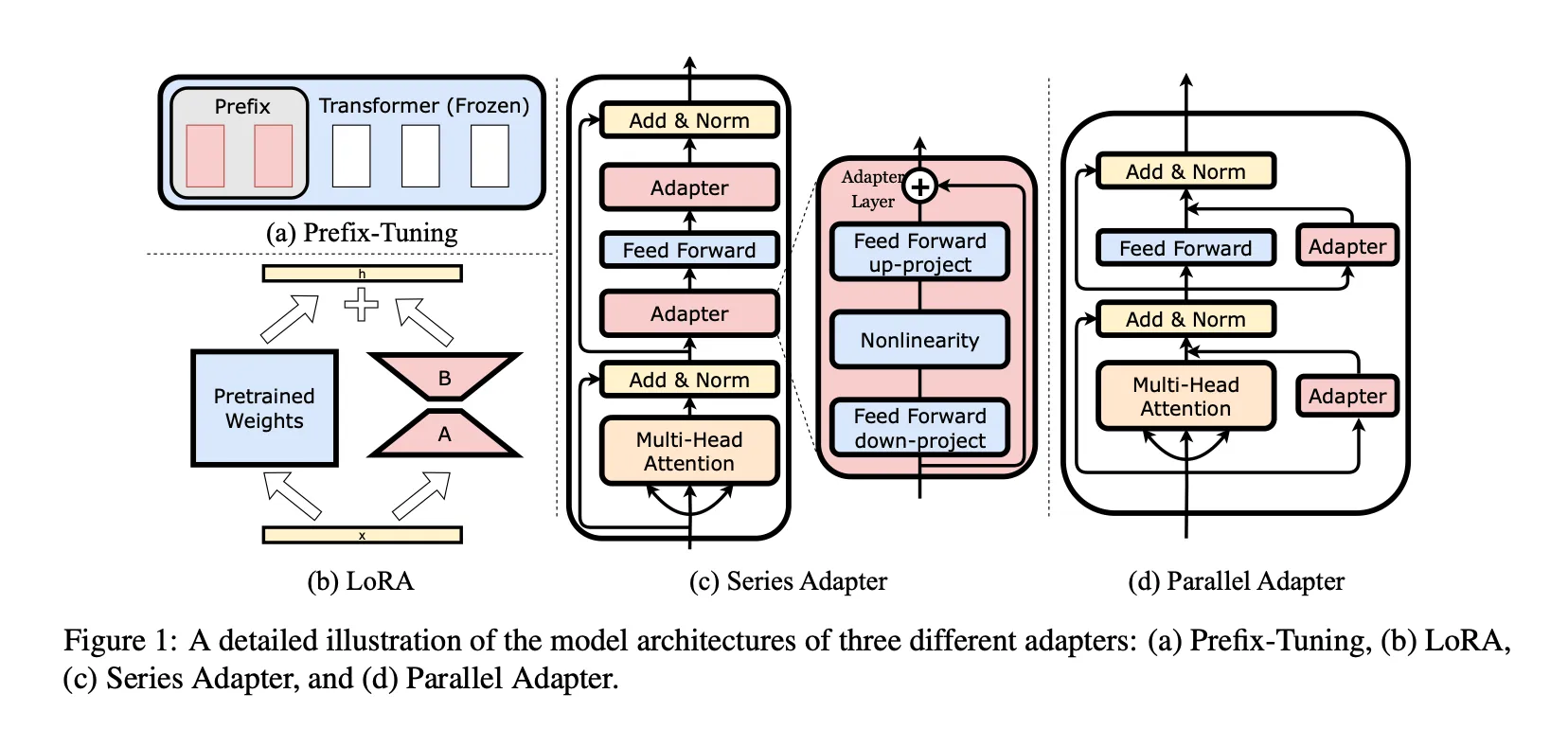
- Series adapter 방법론
  pretraining을 할 때와 모델의 architecture가 달라지니, pretraining 시의 구조에 맞춰 학습된 pretrained weight를 잘 활용되지 못할 수도 있다고 생각한다. 학습 parameter는 줄으나, 추가적인 inference latency도 생기고 pretrained weights도 잘 활용되지 못하니 이 부분이 단점이 될 수 있겠다.
- Parallel adapter 방법론
  architecture에 변화를 주지 않으니(시퀀스적으로 보았을 때 추가적인 블록이 없음), pretrained weight를 잘 활용할 수 있을 것으로 예상된다. 실험 결과를 보니 LLaMA-13B의 경우는 Parallel adapter tuning이 더 좋은 성적을 받은 것도 확인할 수 있다. 하지만 parallel adapter가 생겨 parameter가 증가했으니, inference 시 latency가 느려질 것(adapter가 pretrained weight에 merge 될 수 없고, 이게 LoRA와의 큰 차이)이며, 이게 이 방법론의 단점이다.
- DoRA 방법론
  확실히 magnitude 부분의 학습 파라미터가 추가되니, 같은 rank에서 비교했을 때 학습되는 파라미터 수도 절대적으로 LoRA보다 많아져서 성능 향상이 일어났다고 생각할 수도 있다. 하지만 Rank를 반으로 줄여서 학습 파라미터를 줄였을 때도 LoRA와 비슷하거나 더 좋은 성능을 내는 것을 확인했을 때, DoRA의 학습 능력을 확인할 수 있었다.
- Chat GPT(gpt-3.5-turbo)
  성능이 매우 좋을 것으로 예상했지만, 비교 결과를 봤을 때 그정도는 아닌 것 같다. 그래서 의아했다. 물론 chat gpt는 학습을 시키지 않은 zero-shot chain-of-thought 성능이지만.. gpt-3.5-turbo여서 그런가 싶다. gpt-4의 성능과 비교했으면 어땠을까 궁금해진다.
- etc..
  - Full-finetuning 결과도 있었으면 좋았을텐데 아쉽다.
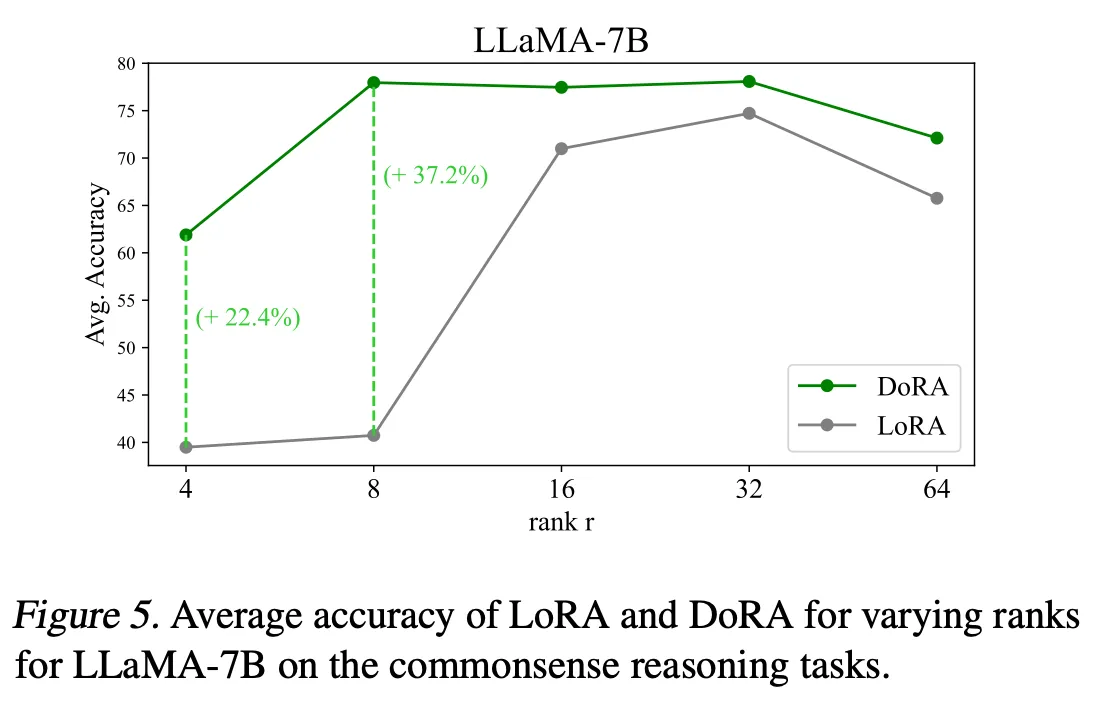
  - DoRA는 LoRA보다 낮은 r을 사용했음에도 성능이 LoRA보다 좋았다 → LoRA의 성능을 높이기 위해서는 더 큰 r을 사용해야 한다는 필요성을 줄여주는 결과다

[LoRA vs DoRA ( $\Delta M, \Delta D)$ )

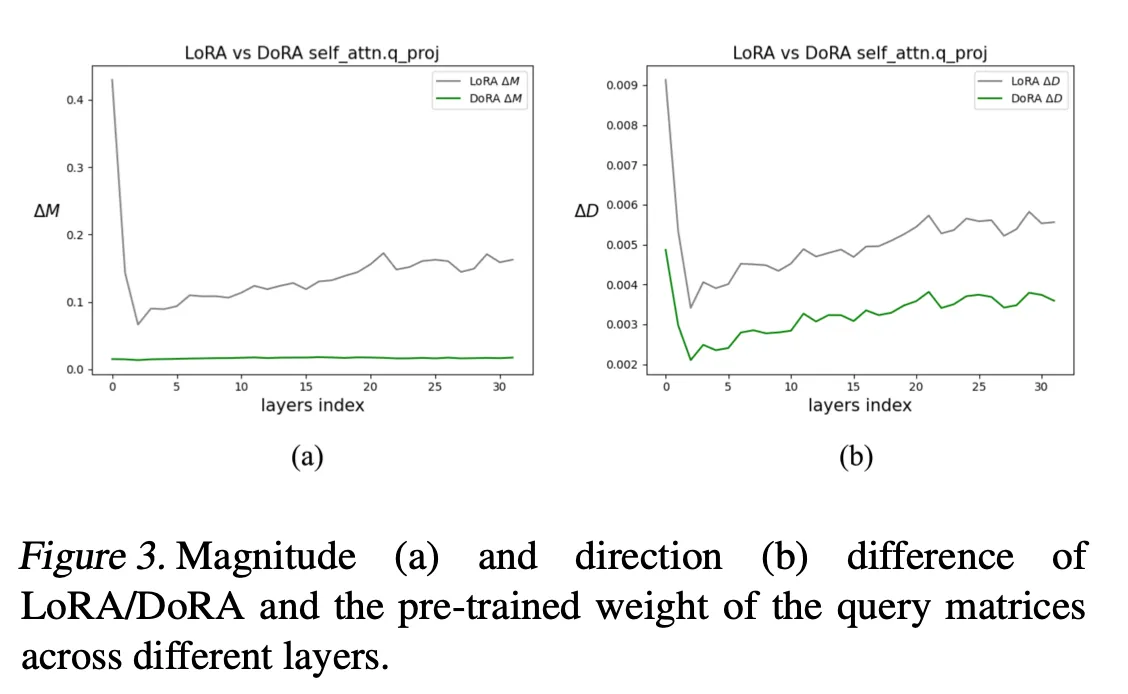
본 논문의 가설: Magnitude update와 direction update의 correlation이 negative correlation을 가질 때 더 optimal하다(이유: pretrained weight는 이미 downstream task에 대한 많은 정보를 가지고 있다)

위의 표를 보면, DoRA의 fine-tuned weight는 direction에서도 magnitude에서도 LoRA의 fine-tuned weight보다 pre-trained weight와 차이가 적다.

DoRA는 Table 1에서 LoRA보다 더 좋은 성능을 보여줬고, 이는 본 논문의 가설이 유효하다고 결론낼 수 있다: 학습이 잘된 foundation model은 downstream adaptation을 위해 direction과 magnitude에서 큰 변화가 필요하지 않다.

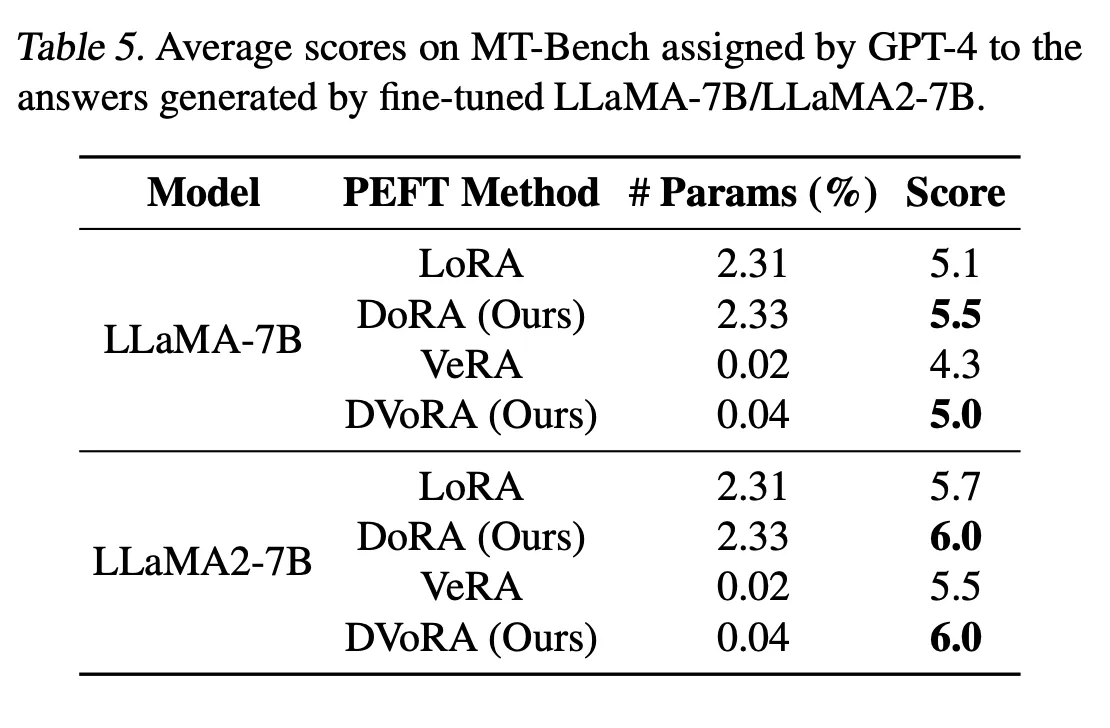
[DoRA를 LoRA의 다른 변형 방법들과 함께 사용할 수 있을까?]

LoRA variant(여기서는 Vera 이용)와 함께 사용했을 때, 긍정적인 결과 얻었음