Image Restoration 이란?

---

Image restoration(이미지 복원) 이라는 단어는 일반 명사처럼 보이지만 영상 처리에서는 어느 정도 고유성을 갖는 단어입니다. Image restoration 이란 화질 저하 현상에 대한 priori knowledge(선험적 지식) 을 사용하여 화질이 저하된 이미지를 재구성하거나 복구하는 프로세스입니다. 화질 저하를 모델링하고, 그 역 프로세스를 적용하여 원본 이미지를 복구합니다. $H$ 와 $\eta$ 에 대한 정보가 많을수록 $\hat{f}(x, y)$ 가 $f(x, y)$ 에 가까워집니다.

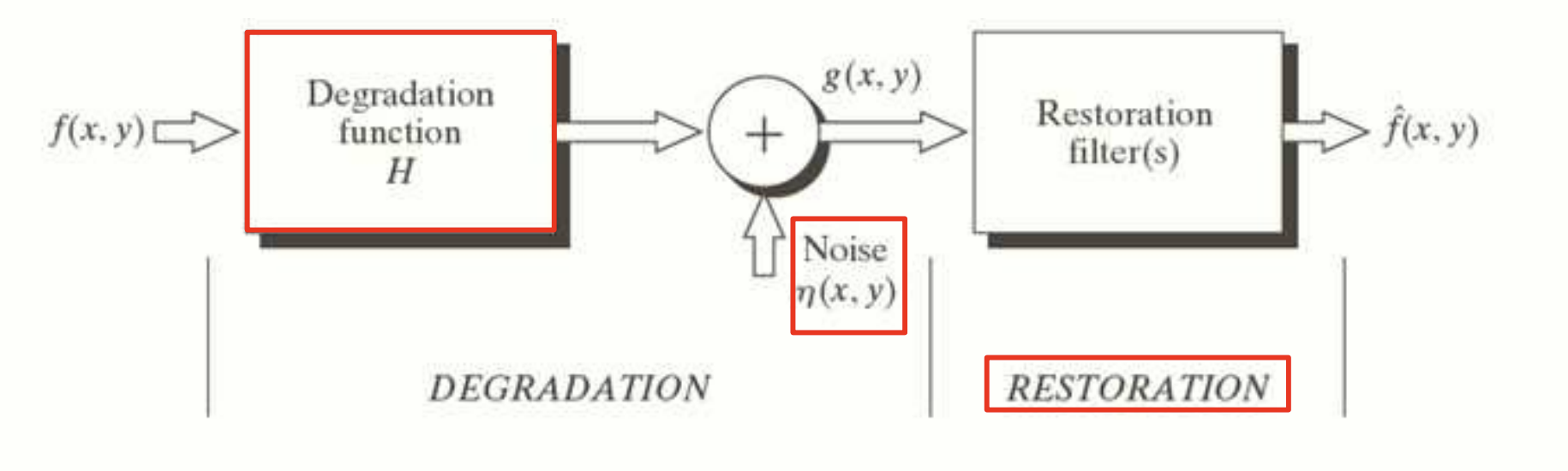
Noise Models

---

공학은 노이즈와의 싸움이라고 해도 과언이 아닐 것입니다. 그리고 노이즈는 우리 주변 어디에든 존재합니다. 예를 들어 CCD 를 이용한 화상 전화 통화에서는 조도, 센서 온도, 무선 네트워크 채널 등이 노이즈 요소로 작용합니다.

Gaussian noise 이란?

가우시안 노이즈는 가장 흔한 노이즈입니다. 수학적 추론 가능성, 중심 극한 정리로 인해 가장 흔하게 분포합니다. 단 두 가지 parameter 로도 표현할 수 있다는 특징을 가집니다.

Uniform noise 이란?

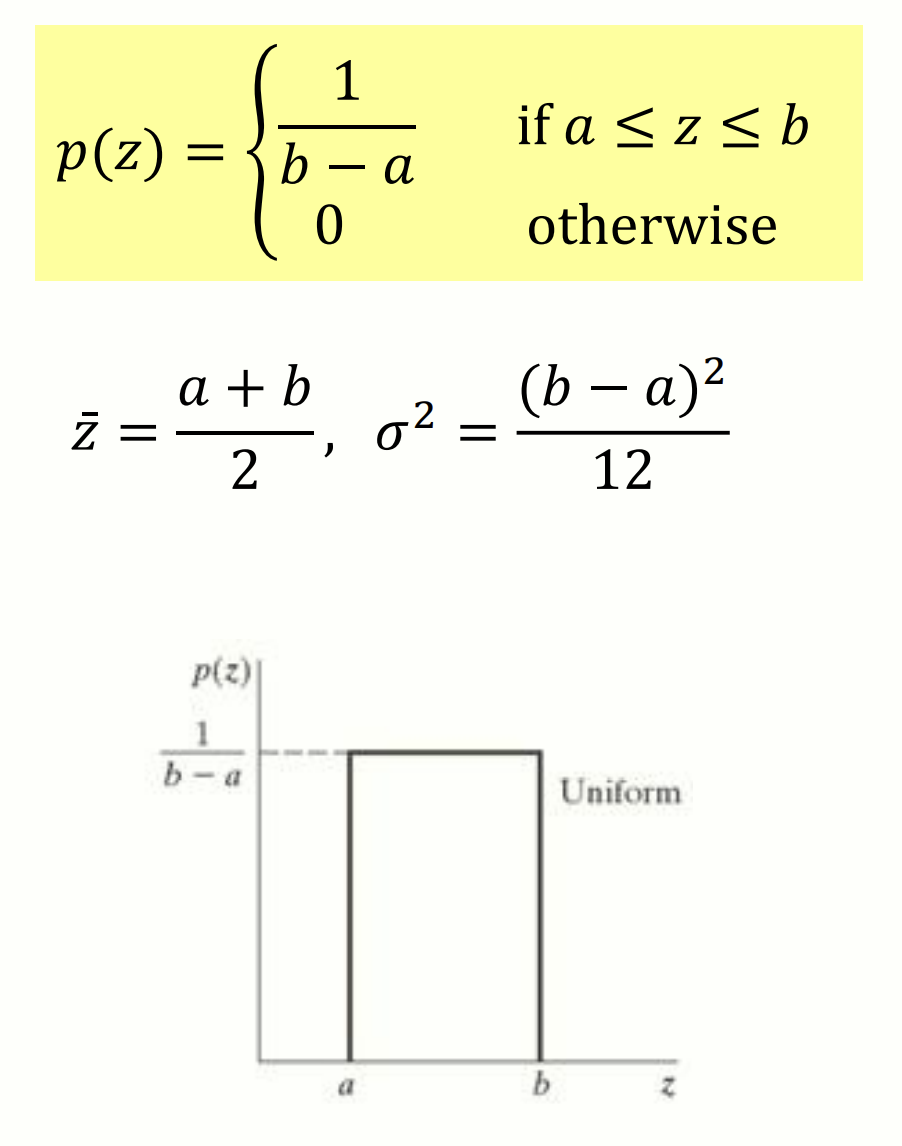
Uniform 분포를 가진 노이즈입니다. 특정 영역 $a$ 부터 $b$ 까지 일정한 분포를 가집니다.

Salt-and-pepper noise 이란?

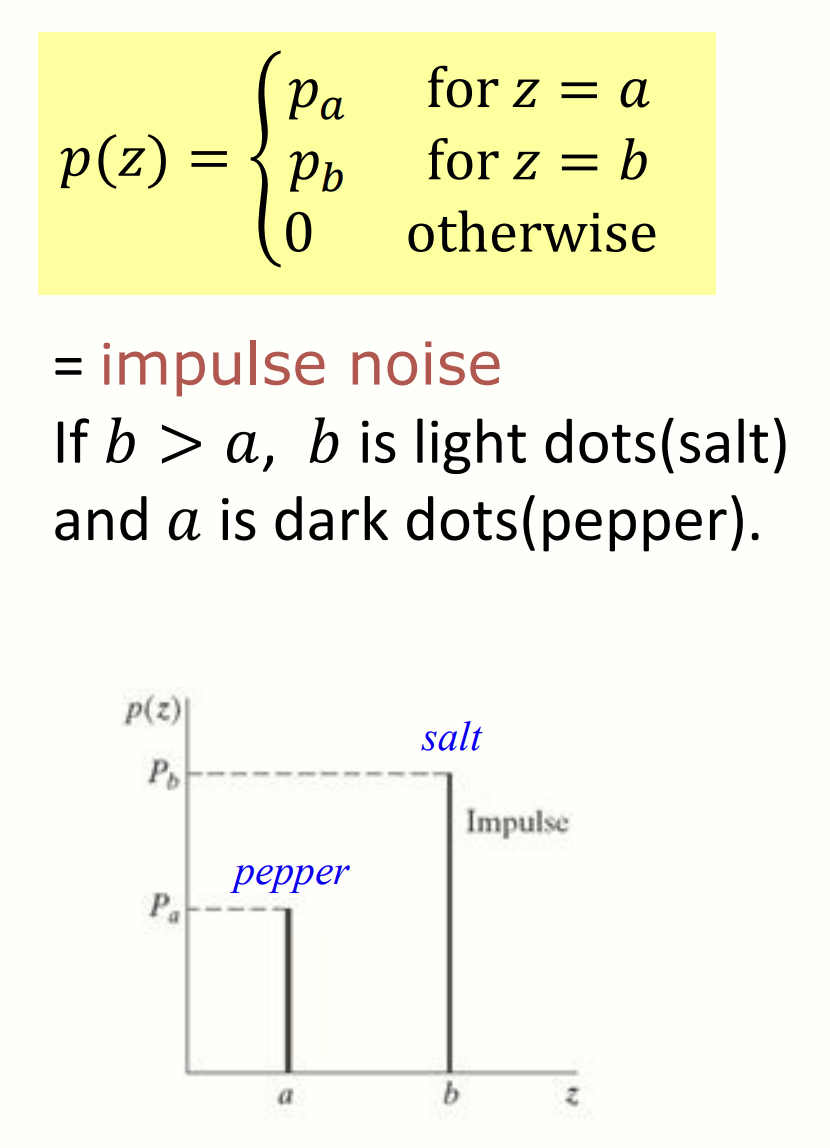
문자 그대로 소금과 후추를 뿌린 것 같은 노이즈입니다. 소금 모양의 노이즈는 높은 값을 가지는 impulse 노이즈, 후추 모양의 노이즈는 낮은 값을 가지는 impulse 노이즈입니다.

노이즈 추측

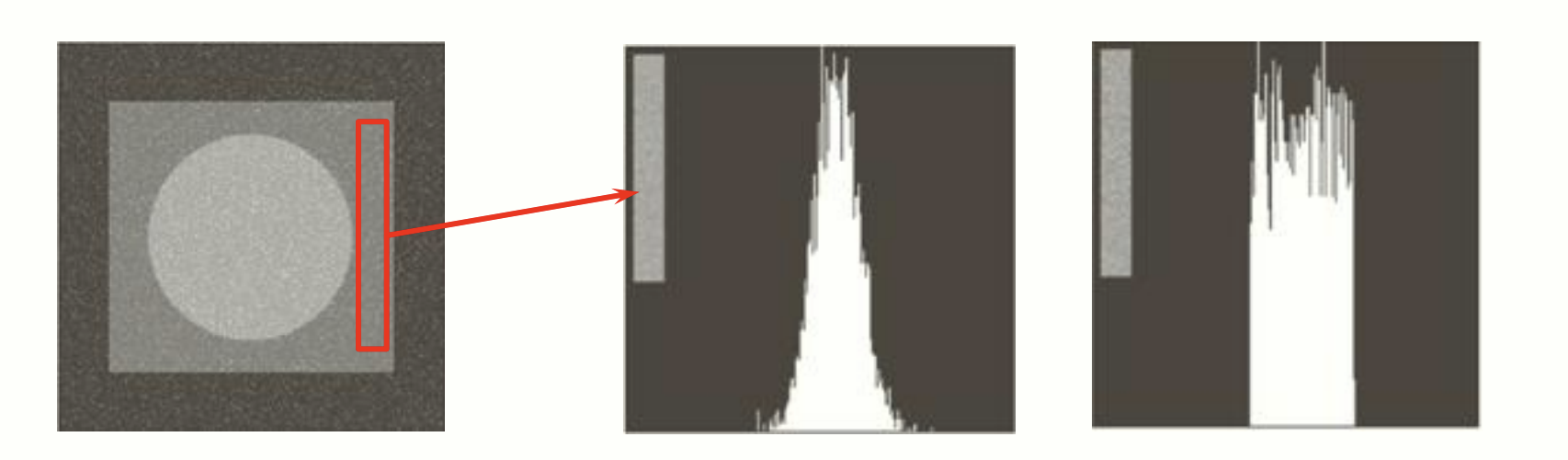
균일한 조건의 이미지 부분을 잘라 mean($\bar{z}$) 와 variance($\sigma^2$) 를 계산하여 노이즈의 종류를 추측할 수 있습니다.

Spatial domain 에서의 resotration

---

Restoration from salt-and-pepper Noise

Impulse noise 라고도 불리는 salt-and-pepper noise 는 이미지 신호의 날카롭고 갑작스러운 교란으로 인해 발생합니다. 이미지에 흰색 또는 검은색(또는 둘 다) 픽셀이 무작위로 흩어져 나타납니다.

import skimage.util as su
from PIL import Image
import numpy as np

img = np.array(Image.open('neck.png'))
# s&p default s:1, p:0, amount=0.01
imgsp = su.random_noise(img, mode='s&p')
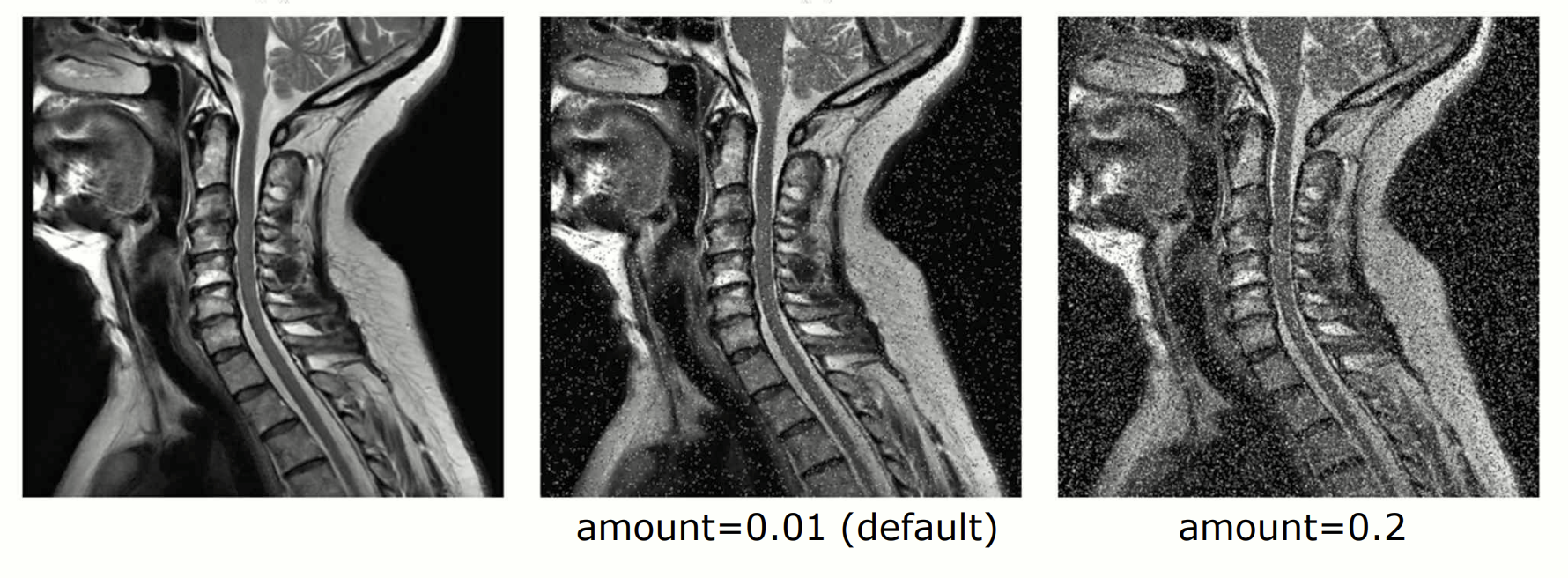
imgsp1 = su.random_noise(img, mode='s&p', amount=0.2)

skimage.util 을 이용하여 salt-and-pepper noise 를 구현할 수 있습니다. 세번째 parameter 인 amount 는 0과 1 사이의 범위로 손상시킬 정도를 지정할 수 있습니다.

Rank-Order Filtering

Median filter 로 Salt-and-pepper noise 를 억제할 수 있습니다. 이 median filter 는 rank-order filter 의 한 종류입니다. Rank-order filter 는 마스크의 모양을 설정하고, 해당 영역의 값을 정렬하여, n번째 값을 선택합니다.
Medain filter 의 예시를 들어봅시다. 5x5 크기의 마스크를 사용하는 median filter는, rank-order filter 에서 n=13 일 때와 동일합니다(5x5 영역에서 가운데 값, 즉 정렬된 값 중 13번째 값을 의미).

import scipy.ndimage as ndi
# cross(십자가) 모양의 필터 마스크
cross = np.array([[0,1,0],
                  [1,1,1],
                  [0,1,0]])
imgro = ndi.rank_filter(imgsp, rank=2, footprint=cross)

Python 에서 rank-order filter 는 scipy.ndimage.rank_filter() 로 구현할 수 있습니다.

scipy.ndimage.rank_filter()

• 2번째 parameter(rank) : 선택할 값의 순위를 나타내며, 0부터 시작합니다.
• 3번째 parameter(footprint): 영역 마스크(필터 모양)를 설정하는 데 사용됩니다.

Outlier Method

Median filter 는 일반적으로 속도가 느릴 수 있습니다. 각 픽셀에 대해 최소 9개의 값을 정렬해야 하므로 시간이 많이 걸립니다. Outlier method 는 이러한 단점을 보완할 수 있는 방법입니다.

기본적인 아이디어는 Salt-and-pepper noise 를 outlier 로 간주하는 것입니다. 회색조 값이 주변 픽셀의 값과 크게 다른 픽셀을 노이즈로 간주하고 제거하는 방식입니다.

Procedure

• 1단계: 임계값(threshold) $D$ 를 선택합니다.
• 2단계: 특정 픽셀의 값 $p$ 를, 해당 픽셀의 8개의 이웃 값(mean $m$)과 비교합니다.
• 3단계: 만약 $|p-m|>D$ 라면, 해당 픽셀 $p$ 를 노이즈로 간주합니다. 그렇지 않으면 정상으로 처리합니다.
• 4단계: 노이즈로 판별된 픽셀은 해당 픽셀 값을 평균 값 $m$ 으로 대체합니다. 노이즈가 아니면 픽셀 값을 그대로 유지합니다.

구현

# av: 8개의 이웃 픽셀에 대한 평균 값을 구하기 위한 마스크
av = array([[1, 1, 1],
			[1, 0, 1],
            [1, 1, 1]] / 8.0

# gsp: salt-and-pepper noise 가 포함된 이미지
gspa = nid.convolve(gsp, av)  # gspa 는 gsp 의 8개 이웃 픽셀에 대한 평균 값
D = 0.2  # threshold
r = (abs(gsp - gspa) > D) * 1.0  # |p - m| > D 인 경우 r = 1, 아니면 r = 0
outimg = r * gspa + (1 - r) * gsp

Threshold D 가 높을수록 필터링 효과도 크다.

Restoration from Gaussian Noise

Image Averaging

100개의 이미지 복사본이 주어졌고, 각 이미지에는 Gaussian noise 가 포함되었다고 가정해봅시다. $M$ 은 원본 이미지, $N_{i}$ 는 각 이미지에 더해진 Gaussian noise, $M\prime$ 는 복원된 이미지라면 다음과 같은 수식을 만들 수 있습니다.

이미지 복사본(샘플 수)이 많을수록, 즉 $N_{i}$ 의 개수가 많아질수록, 평균화된 결과는 노이즈가 감소하며 원래 이미지에 가까워집니다.

Minimum Mean-Square Error Filter

Noise 가 반드시 평균 0의 정규분포를 따르지 않아도 작동합니다.

• $m_{f}$ : 마스크 내의 평균 값
• $\sigma_f^2$ : 마스크 내의 분산
• $\sigma_g^2$ : 이미지 전체의 분산
• $g$ : 현재 픽셀 값

지역 분산 $\sigma_f^2$ 가 크면:

• 출력 값은 $g$(현재 픽셀 값)에 가깝습니다.
• 경계(edge)가 유지됩니다.
• 마스크 내 pixel values 가 다양하다면, 현재 픽셀의 값이 그대로 유지되어 이미지의 경계가 흐려지지 않습니다.

지역 분산 $\sigma_f^2$ 가 작으면:

• 출력 값은 $m_f$(마스크 평균 값) 에 가깝습니다.
• 배경(background)가 평균화됩니다.
• 마스크 내 pixel values 가 비슷하다면, 노이즈가 포함된 픽셀을 마스크 평균 값을 대체하여 부드러운 배경을 만듭니다.

일반적인 LPF 보다 효과적으로 Gaussian noise 를 제거합니다. 이미지의 지역적 특성을 기반으로 동작하므로, noise 가 다양한 영역에서도 적절히 처리됩니다. 하지만 경계(edge)와 고주파 성분이 부드럽게 되어 흐려지는 경향이 있습니다. 이러한 단점은 마스크의 크기가 클수록 두드러집니다.

Wiener filter

Wiener 필터는 입력 이미지와 출력 이미지 간의 차이(오차)의 제곱합을 최소화하도록 작동합니다. 주로 frequency domain 에서 사용되지만, spatial domain 에서도 적용할 수 있습니다.

출력 값 계산

• $m_f$ : 마스크 내 픽셀의 평균 값
• $\sigma^2_f$ : 마스크 내 픽셀의 분산
• $n$ : 이미지 전체의 노이즈 분산 값(평균적으로 계산된 값)
• $g$ : 현재 픽셀 값

동작 원리

Noise 분산($n$) 과 지역 분산($\sigma^2_f$)의 비교에 따라 다르게 동작합니다:

• $\sigma^2_f$ >> $n$ (지역 분산이 큰 경우):
  • 경계선(edge)을 유지하며 출력 값이 현재 픽셀 값 $g$ 에 가깝게 계산됩니다.
  • 즉, 경계와 디테일을 보존합니다.
• $\sigma^2_f$ << $n$ (지역 분산이 작은 경우):
  • 배경(background)을 부드럽게 처리하며 출력 값이 마스크 평균 값 $m_f$ 에 가깝게 계산됩니다.
  • 즉, 노이즈를 제거하고 배경을 평탄화합니다.

구현

from scipy.signal import wiener
out1 = wiener(img, [3, 3])  # 3x3 마스크를 사용한 Wiener 필터 적용
out2 = wiener(img, [5, 5])  # 5x5 마스크를 사용한 Wiener 필터 적용
out3 = wiener(img, [7, 7])  # 7x7 마스크를 사용한 Wiener 필터 적용
out4 = wiener(img, [9, 9])  # 9x9 마스크를 사용한 	Wiener 필터 적용

• 마스크 크기가 커질수록 노이즈 제거 효과는 커지지만, 디테일이 더 많이 부드러워집니다.
• scipy.signal.wiener 함수는 이미지와 마스크 크기를 입력받아 Wiener 필터를 적용합니다.

예시

낮은 분산(평탄한 영역)의 이미지를 처리할 때 뛰어난 성능을 발휘합니다. 배경을 부드럽게 하면서도 경계선의 뚜렷함을 유지하려고 합니다. 하지만 노이즈 제거 과정에서 고주파 성분이 감소하여 경계가 약간은 흐릿해질 수도 있습니다.

Frequency domain 에서의 restoration

---

Periodic noise

Periodic noise 가 freq domain 에서 제거하기 유리한 이유

Periodic noise 는 spatial domain 에서는 이미지 전체에 걸쳐 반복되는 패턴으로 나타납니다. 하지만 freq domain 에서는 특정 주파수에 집중된 성분으로 나타납니다. 이 말은, sinusoidal noise 가 이미지에서 일정한 간격으로 반복되기 때문에 특정한 주파수 성분에서만 강하게 나타난다는 뜻입니다.

Frequency domain 에서는 periodic noise 가 특정 주파수 위치에 peak 로 나타납니다.

Frequency domain 에서 noise 가 가운데에 몰려있음을 알 수 있다.

Band Reject Filter

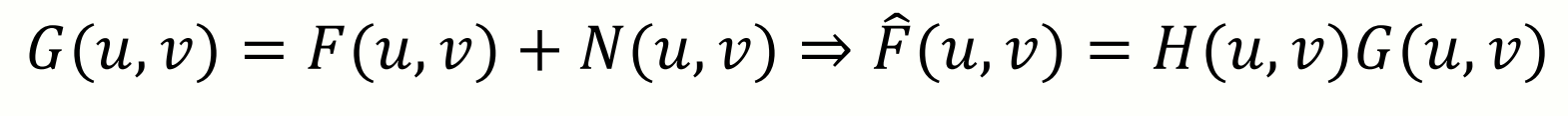
Band reject filter 는 특정 주파수 범위(대역)의 성분을 차단하고, 나머지 주파수 성분은 통과시키는 필터입니다. Noise 성분이 이미 잘 알려진 위치에 있는 경우 사용하는 필터입니다. 대표적인 band reject filter 는 다음과 같습니다:

• Ideal band reject filter
  • 완전히 차단 대역의 주파수를 제거하는 이상적 필터.
  • 이상적이지만 실제 구현 시 경계에서 인위적인 왜곡이 발생할 수 있다.
• Butterworth band reject filter
  • 차단 대역 가장자리에서 완만한 경사를 가지는 필터.
  • 차단 대역 내의 주파수를 점직적으로 억제하여 더 자연스러운 필터링 제공.
• Gaussian band reject filter
  • Gaussian distribution 형태로 특정 대역을 차단.
  • 차단 대역의 경계가 매우 부드러워 가장 자연스러운 방식.

핵심 요소

1. 차단 중심 주파수 ($d$): 차단하고자 하는 대역의 중심 주파수입니다. Freq domain 의 중심에서의 거리로 표현됩니다.
   ex) 중심에서 반경 d = 100 에 노이즈가 집중되어 있다면, 이 값을 필터의 중심으로 설정합니다.
2. 대역폭 ($k$): 차단할 주파수 범위의 너비를 설정합니다. 필터가 차단하는 영역은 $d-k$ 부터 $d+k$ 까지의 거리입니다.

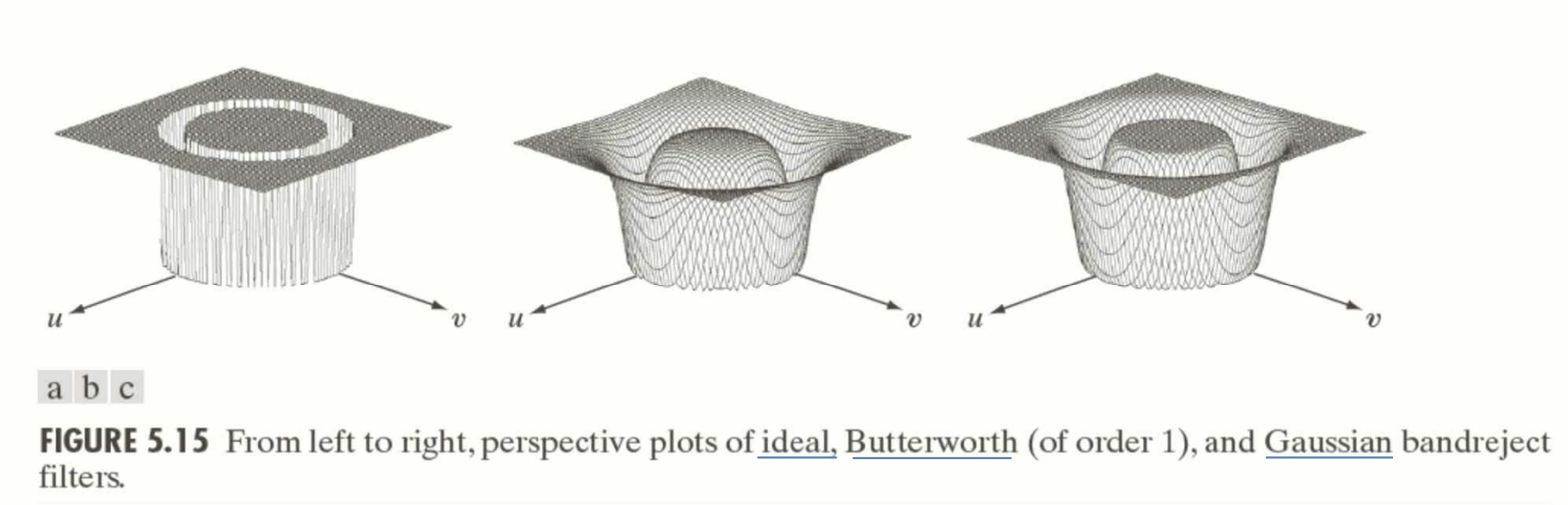
오른쪽부터 순서대로 ideal, Butterworth, Gaussian band reject filter.

Band reject filter 의 수식

수학적으로 Band reject filter 는 다음과 같이 표현됩니다:

• $D(u, v)$ : Freq domain 에서 중심 좌표(DC 성분) 로부터 특정 주파수 좌표 $(u, v)$ 까지의 거리
• $d$ : 필터 중심 주파수(노이즈가 있는 거리)
• $k$ : 대역폭(차단 범위의 너비)
• $H(u, v)$ : 필터의 전달 함수, 0은 차단, 1은 통과

구현

from numpy.fft import fft2, ifft2, fftshift, ifftshift
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image

# 1. 이미지 불러오기 및 Fourier Transform
img = np.array(Image.open('lena_noise.png').convert('L'))
img_fft = fftshift(fft2(lena_noise))

# 2. DC 성분 제거 및 최대값 좌표 찾기
dc_removed = np.abs(img_fft).copy()
de_removed[128, 128] = 0	# 중심 좌표
i, j = np.where(dc_removed == dc_removed.max())  # DC 제외한 최대값 좌표 찾기

# 3. 거리 계산을 위한 격자 생성
x, y = np.ogrid[:img_fft.shape[0], :img_fft.shape[1]]
center_x, center_y = 128, 128  # 중심 좌표
distance_grid = np.sqrt((x - x_center)**2 +(y - y_center)**2)  # 거리 계산

# 4. Band Reject Filter 생성
k = 1	# 대역폭
d = np.sqrt((i[0] - center_x)**2 + (j[0] - center_y)**2)  # 중심에서 노이즈까지의 거리
band_reject_filter = (distance_grid < (d - k)) | (distance_grid > (d + k))

# 5. 필터 적용
filtered_img_fft = img_fft * band_reject_filter

# 6. IFFT 로 복원
restored_img = np.abs(ifft2(ifftshift(filtered_img_fft)))

# 7. 결과 시각화
plt.figure(figsize=(12, 8))

# 원본 이미지
plt.subplot(2, 2, 1)
plt.title('Original Image')
plt.imshow(img, cmap='gray)
plt.axis('off')

# 주파수 스펙트럼
plt.subplot(2, 2, 2)
plt.title('Frequency Spectrum')
plt.imshow(np.log(abs(img_fft) + 1), cmap='gray')
plt.axis('off')

# 필터 마스크
plt.subplot(2, 2, 3)
plt.title('Band Reject Filter')
plt.imshow(band_reject_filter, cmap='gray')
plt.axis('off')

# 복원된 이미지
plt.subplot(2, 2, 4)
plt.title('Restored Image')
plt.imshow(restored_img, cmap='gray')
plt.axis('off')

plt.tight_layout()
plt.show()

1. 거리 계산:
   • Freq domain 의 각 좌표에서 중심 좌표(DC 성분)까지의 거리를 계산.
   • 거리 값은 2D 배열(distance_grid)로 저장.
2. 필터 생성:
   • distance_grid 와 중심 거리 d, 대역폭 k 를 비교하여 차단 범위에 해당하는 주파수를 결정.
   • $d-k \leq \leq d+k$ : 차단(0)
   • 나머지: 통과(1)
3. 필터 적용:
   • 필터를 freq domain 에 곱하여 차단 범위 내의 주파수 성분을 제거.
4. 역변환:
   • 필터링된 freq domain 를 IFFT 하여 spatial domain 이미지로 복원.

LSI 와 추가적인 noise

이미지는 다양한 왜곡을 겪을 수 있는데, 이는 선형 이동 불변 모델(Linear Shift Invariant Model) 과 추가적인 노이즈(Additive noise)로 설명됩니다. 이미지를 복원하려면 이러한 왜곡의 특성을 이해하고 제거하는 작업이 필요합니다.

LPI 왜곡 모델

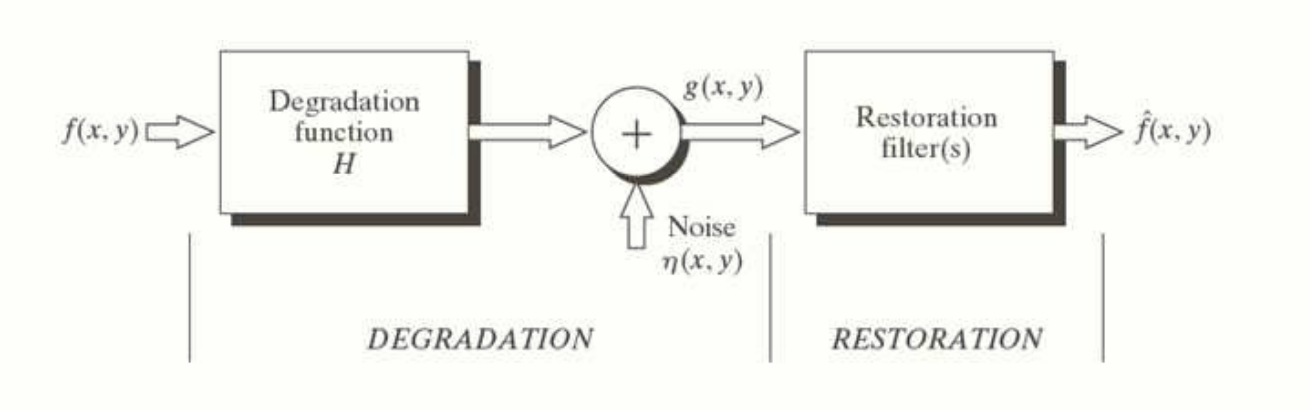
• $g(x, y)$ : 왜곡된 이미지
• $H[f(x, y)]$ : 입력 이미지 $f(x, y)$ 에 적용된 왜곡 연산자 $H$
• $\eta(x, y)$ : 추가적인 노이즈(additive noise)

모델의 특성

• 덧셈 법칙:
  $H[f_1(x, y) + f_2(x, y)] = H[f_1(x, y)] + H[f_2(x, y)]$
• 동질성(Homogeneity):
  $H[a f(x, y)] = a H[f(x, y)]$
  위치 불변성:
  $H[f(x, y)] = g(x, y) \implies H[f(x-\alpha, y-\beta)] = g(x-\alpha, y-\beta)$

LPI system 수식

• $*$ 컨벌루션(Convolution, 합성곱)
• $h(x, y)$ : 점 확산 함수(PSF)로, 시스템의 왜곡 특성을 나타냄
• $\eta(x, y)$ : 추가적인 노이즈

Freq domain 으로의 변환은 다음과 같이 계산됩니다:

• $G(u, v)$ : 왜곡된 이미지의 주파수 표현
• $H(u, v)$ : 시스템의 주파수 응답
• $F(u, v)$ : 원본 이미지의 주파수 표현
• $N(u, v)$ : 노이즈의 주파수 표현

점 확산 함수(PSF)의 종류

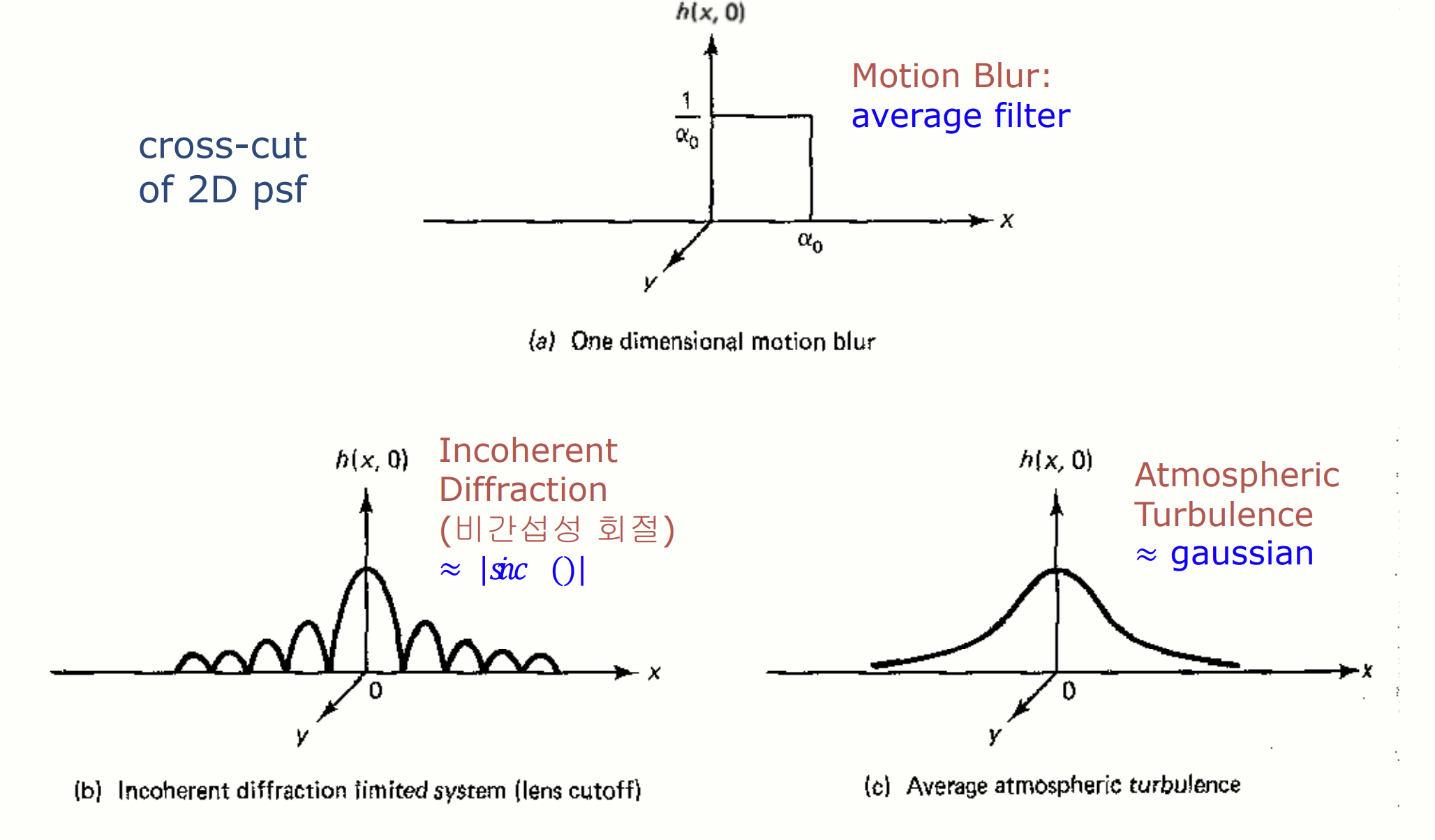
1. Motion Blur: $h(x, y)$ 는 일정한 길이의 직사각형 형태를 가지며, 평균 필터와 비슷한 역할을 합니다. 이미지가 움직이는 동안 노출되면 발생합니다.

2. 비간섭성 회절(Incoherend Diffraction): PSF 가 Sinc 함수 $|sinc|$ 형태를 가집니다. 렌즈의 초점 문제가 주된 원인입니다.

3. 대기 난류(Atmospheric Turbulence): PSF 가 Gaussian 형태를 가집니다. 대기 조건으로 인해 이미지의 선명도가 떨어질 때 발생합니다.

Motion Blur

Motion blur 는 카메라나 피사체의 움직임으로 인해 이미지가 흐려지는 현상을 나타냅니다. 이러한 현상은 조리개가 열려 있는 동안(노출 시간 $T$) 발생하며, 다음과 같은 수식으로 모델링됩니다:

• $g(x, y)$ : blur 처리된 이미지
• $f(x, y)$ : 원본 이미지
• $x_0(t), y_0(t)$ : 시간 $t$ 에 따른 피사체의 이동 경로
• $T$ : 노출 시간

Fourier Transform 을 통한 표현

Spatial domain 에서의 bluring 모델을 freq domain 으로 변환합니다:

• $F(u, v)$ : 원본 이미지의 주파수 변환
• $H(u, v)$ : motion blur 를 나타내는 전달 함수

• $a, b$ : $x$ 와 $y$ 방향의 이동 속도
• $ua + ub$ : 이동 방향에 따른 주파수 성분

a, b = 0.1, T = 1

Atmospheric Turbulence

Atmospheric turbulence 는 먼 거리에서 찍은 이미지에 발생하는 흔들림과 흐림 현상을 나타냅니다. 이는 다음과 같은 함수로 모델링됩니다:

• $H(u, v)$ : 난류의 영향을 나타내는 필터(전달 함수)
• $k$ : 난류의 강도를 나타내는 상수. $k$ 값이 클수록 이미지가 더 심하게 흐려짐
• $u, v$ : frequency 좌표

Atmospheric turbulence 는 고주파를 억제하여 이미지의 디테일을 손실시킨다.

Inverse Filtering

Inverse filtering 은 blur 또는 noise 로 열화된 이미지를 복원하려는 방법 중 하나입니다. 이미지가 열화되는 과정이 수학적으로 모델링 될 수 있다면, 이를 거꾸로 되돌려 원본 이미지를 추정하는 방식입니다.

이미지 열화 과정

• $g(x, y)$ : 열화된 이미지(blurred image)
• $h(x, y)$ : Blur 의 원인이 되는 필터
• $f(x, y)$ : 원본 이미지
• $\eta(x, y)$ : Noise
• $*$ : 컨벌루션 연산

Frequency Domain 으로 변환

Inverse Filtering

열화된 이미지에서 원본을 복원하려면 $H(u, v)$ 로 나눕니다:

• $\hat{F}(u, v)$ : 복원된 이미지의 주파수 표현

문제점

$H(u, v)$ 가 0 또는 매우 작으면, 노이즈 성분 $\frac{N(u, v)}{H(u, v)}$ 가 급격히 커집니다. 결과적으로, 복원된 이미지가 왜곡될 가능성이 큽니다. 필터링 후 고주파 성분이 노이즈와 함께 증폭될 수 있으므로, 이를 해결하기 위해 Hanning, Hamming 과 같은 smoothing filter 를 적용하여 noise 영향을 완화시키기도 합니다.

구현

from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
from numpy.fft import fft2, fftshift, ifft2

# 1. 이미지 불러오기
image = Image.open('buffalo.png').convert('L')
b = np.array(image, dtype=np.float32)

# 2. Fourier transform 및 중앙 정렬
bf = fft2(b)  # 2D Fourier transform
bf_shifted = fftshift(bf)  # 주파수 성분을 중앙으로 정렬

# 3. 주파수 격자 생성
r, c = b.shape  # 이미지의 높이와 너비
x, y = np.meshgrid(np.linspace(-c/2, c/2, c), np.linspace(-r/2, r/2, r))

# 4. Butterworth filter 생성
D = 15  # Cutoff 주파수
order = 2  # 필터의 차수
bworth = 1 / (1 + ((x**2 + y**2) / D**2)**order)  # Butterworth filter 공식

# 5. Blur 처리 (frequency domain 에서 필터 적용)
bw = bf_shifted * bworth  # frequency domain 에서 필터링
bwa = np.abs(ifft2(ifftshift(bw)))  # spatial domain 으로 복원

# 6. Inverse Filtering (복원)
bwa_freq = fft2(bwa)
bwa_freq_shifted = fftshift(bwa_freq)

# Inverse Filtering 적용
inverse_filtered_freq = bwa_freq_shifted / bworth  # freq domain 에서 inverse filtering
inverse_filtered_freq[np.isinf(inverse_filtered_freq)] = 0  # 0으로 나누는 경우 처리
inverse_filtered_freq[np.isnan(inverse_filtered_freq)] = 0  # NaN 처리

# Spatial domain 으로 복원
inverse_filtered = np.abs(np.fft.ifft2(np.fft.ifftshift(inverse_filtered_freq)))

# 7. 결과 시각화
plt.figure(figsize=(10, 5))

# 원본 이미지
plt.subplot(1, 3, 1)
plt.title("Original Image")
plt.imshow(b, cmap="gray")
plt.axis("off")

# Blur 처리된 이미지
plt.subplot(1, 3, 2)
plt.title("Blurred Image (LPF Applied)")
plt.imshow(bwa, cmap="gray")
plt.axis("off")

# 복원 이미지
plt.subplot(1, 3, 3)
plt.title("Inverse Filtered Image")
plt.imshow(inverse_filtered, cmap="gray")
plt.axis("off")

plt.tight_layout()
plt.show()

Pseudo Inverse Filtering

Pseudo inverse filtering 은 inverse filtering 의 단점을 보완하기 위해 고안된 방법입니다. Inverse filtering 은 $H(u, v)$ 가 0이거나 아주 작은 값일 때, noise 가 증폭되는 문제가 있습니다. Pseudo inverse filtering 는 이러한 문제를 해결하기 위해 $H(u, v)$ 값이 작은 경우에 대한 조건을 추가로 설정합니다.

• $d$ : 임계값(threshold). 너무 작은 값을 보정하여 noise 증폭을 줄임.

구현

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt

# 1. 이미지 불러오기
image = Image.open("buffalo.png").convert("L")
blurred_image = np.array(image, dtype=np.float32)

# 2. Fourier 변환 및 주파수 중심 정렬
blurred_freq = np.fft.fft2(blurred_image)          # 푸리에 변환
blurred_freq_shifted = np.fft.fftshift(blurred_freq)  # 주파수 중앙 정렬

# 3. Butterworth 필터 생성
r, c = blurred_image.shape
x, y = np.meshgrid(np.linspace(-c/2, c/2, c), np.linspace(-r/2, r/2, r))
D = 15  # Cutoff 주파수
order = 2
bworth = 1 / (1 + ((x**2 + y**2) / D**2)**order)

# 4. Pseudo Inverse Filtering
d = 0.01  # 임계값(Threshold)
pseudo_inverse_filter = np.copy(bworth)
pseudo_inverse_filter[np.abs(bworth) < d] = d  # 작은 값 보정

# 5. 역 필터링 적용
restored_freq = blurred_freq_shifted / pseudo_inverse_filter  # 역 필터링
restored_freq[np.isnan(restored_freq)] = 0  # NaN 처리
restored_freq[np.isinf(restored_freq)] = 0  # inf 처리

# 6. 공간 도메인으로 복원
restored_image = np.abs(np.fft.ifft2(np.fft.ifftshift(restored_freq)))

# 7. 결과 시각화
plt.figure(figsize=(10, 5))

# 원본 블러 이미지
plt.subplot(1, 2, 1)
plt.title("Blurred Image")
plt.imshow(blurred_image, cmap="gray")
plt.axis("off")

# 복원된 이미지
plt.subplot(1, 2, 2)
plt.title("Pseudo Inverse Filtered Image")
plt.imshow(restored_image, cmap="gray")
plt.axis("off")

plt.tight_layout()
plt.show()

Wiener Filter

Wiener 필터는 이미지 복원에서 최소 평균 제곱 오차(Minimum Mean Square Error, MMSE)를 기반으로 한 필터로, noise 와 blur 효과를 동시에 처리할 수 있는 방식입니다.

핵심 개념

• Inverse filter 의 한계: Inverse filter 는 noise 를 고려하지 않기 때문에 노이즈가 있는 이미지에서는 효과적으로 복원되지 않을 수 있습니다.
• Wiener filter 의 접근: Wiener filter 는 복원 과정에서 이미지의 blur 과 noise 를 통계적 특성을 결합하여 더 좋은 결과를 제공합니다.

수식

Wiener filter 의 공식은 다음과 같습니다:

• $H(u, v)$ : Blurring 을 나타내는 Degradation 모델
• $S_\eta(u, v)$ : Noise 의 파워 스펙트럼
• $S_f(u, v)$ : 원본 이미지의 파워 스펙트럼
• $G(u, v)$ : Degradation 및 noise 가 적용된 이미지

여기서 $\frac{S_\eta(u, v)}{S_f(u, v)}$ 를 $K$ 로 나타내면

로 표현할 수 있습니다.

$K$ 의 역할

$K$ 값이 클수록 noise 억제가 강해지며, 필터링된 이미지가 더 부드러워집니다. $K$ 값이 작을수록 noise 억제는 약하지만 더 선명한 복원이 가능합니다.

Bandpass 특성

Wiener filter 는 bandpass 특성을 가지며, 특정 주파수 대역을 강조하고 다른 대역은 억제합니다:

• Inverse filter 는 High-pass 특성을 가짐
• Mean filter 는 Low-pass 특성을 가짐
• Wiener filter 는 이 두 가지 사이의 bandpass 특성을 가짐

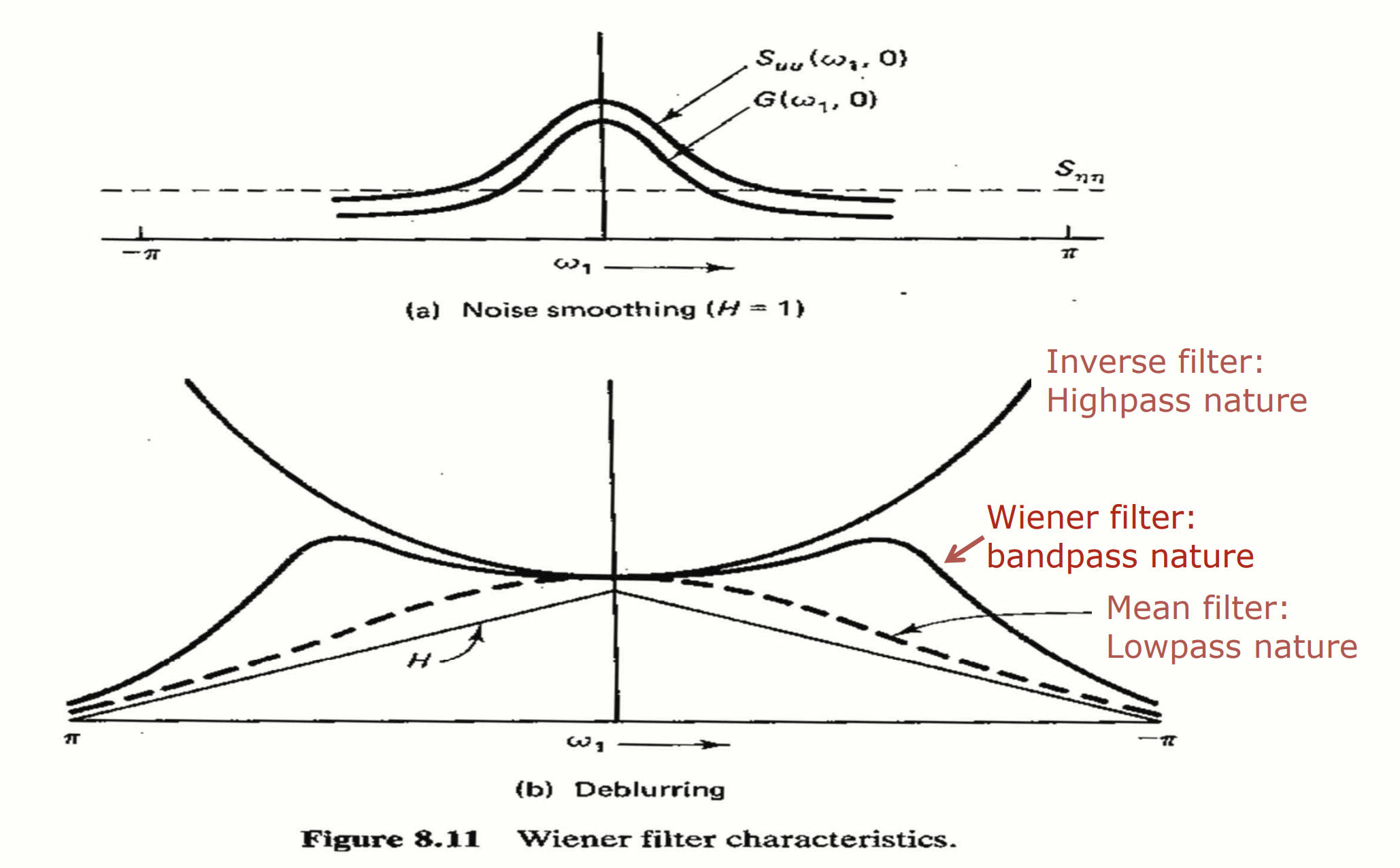
구현

K = 0.01
bf = fftshift(fft2(blur))  # 입력 블러 이미지를 푸리에 변환
# H(u, v): 블러를 나타내는 Butterworth LPF
w1 = bf * (abs(bworth)**2 / (abs(bworth)**2 + K) / bworth)
w1a = abs(ifft2(w1))  # Wiener 필터가 적용된 복원 이미지
io.imshow(w1a)