Image Segmentation

파워·2024년 11월 23일

목록 보기

6/10

Segmentation 이란?

Segmentation(분할) 이란 이미지를 구성 요소로 나누거나 서로 분리된 객체로 구분하는 작업입니다. 우리는 두 가지 주요 방법인 thresholding(임계값 처리) 과 edge detection(엣지 검출) 을 다룰 것입니다.

Thresholding

Single Thresholding

Single thresholding 은 이미지를 binary 이미지로 변환하는 과정입니다. 각 픽셀의 값이 지정한 임계값 $T$ 보다 크거나 작음에 따라 흰색(1) 또는 검은색(0) 으로 변환됩니다.

원리

픽셀 값 $f(x, y)$ 가 $T>f(x, y)$ 이면 흰색으로 변환합니다.
그렇지 않으면 검은색으로 변환합니다.

구현

import numpy as np
from PIL import Image

# 이미지를 읽어서 변수 f 에 저장
f = np.array(Image.open('flying.png'))

# 임계값 T = 50 을 설정하여 binary image 로 변환
binary_image = (f < 50)  # 논리 연산: 픽셀 값이 50보다 작은 부분만 True

# 데이터 타입 확인
print(binary_image.dtype)  # 출력 결과: bool

# bool 타입을 float64로 변환(추후 계산을 위해)
binary_image_float = binary_image.astype('float64')

# 변환된 데이터 타입 확인
print(binary_image_float.dtype)  # 출력 결과: float64

예시

적절한 T 설정을 통해 쌀알과 박테리아의 주요 객체만 강조되었다.

적절한 T 를 설정하지 못하면 오히려 필요 없는 디테일이 살아난다.

Double Thresholding

두 가지 임계값 T 를 설정하면 더 정교하게 segmentation 을 수행할 수 있습니다.

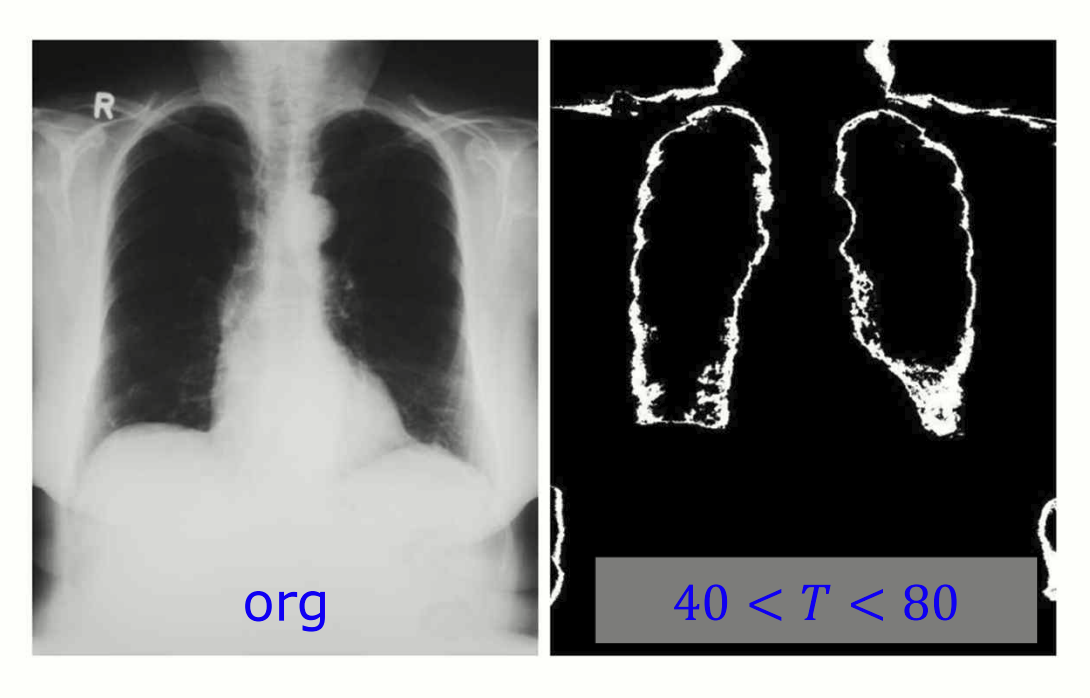
환자의 폐를 double thresholding 을 통해 segmentation 한 이미지.

Thresholding 의 사용처

불필요한 세부 사항 제거

임계값 처리를 사용하여 이미지에서 중요한 객체만 남기고, 불필요한 배경 세부사항을 제거할 수 있습니다.
예: 쌀과 박테리아 이미지를 처리할 때, 배경을 제거하고 객체만 남길 수 있습니다.

숨겨진 세부 사항 강조

임계값 처리를 통해 종이의 패턴이나 척추 이미지와 같은 미세한 세부사항을 강조할 수 있습니다.
이는 이미지의 특정 영역을 명확히 드러내는 데 유용합니다.

다양한 배경(background) 제거

이미지에서 배경이 불균일하거나 변화가 많을 때, 임계값 처리를 통해 이를 제거하고 객체를 명확히 분리할 수 있습니다.
예: 택스트 이미지에서 noise 배경을 제거하고 텍스트만 남기는 데 사용됩니다.

T > 100 을 적용하여 noise 를 제거하고 텍스트를 명확히 분리한 결과.

임계값 선택은 이미지의 binary 품질에 크게 영향을 미친다.

히스토그램 분석

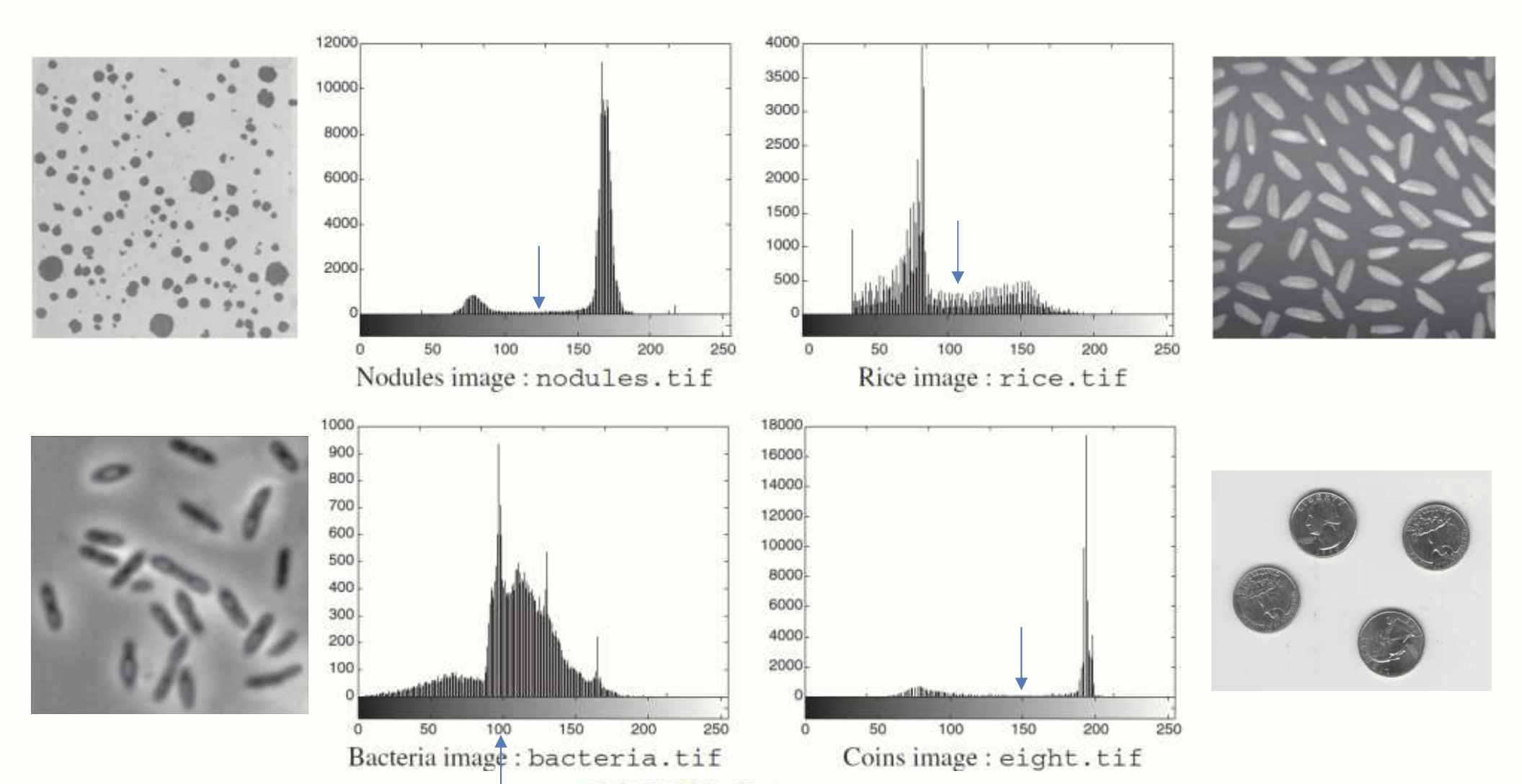
히스토그램을 이용하면 background 와 객체가 어떤 pixel values 분포를 갖는지 쉽게 확인하여 적절한 임계값을 찾는데 도움을 줍니다. 하지만 사람의 눈으로 히스토그램을 일일이 확인하는 것은 매우 번거로우며 정확도도 떨어질 수 있습니다. 히스토그램을 이용하여 적절한 임계값 $T$ 를 선택하는 알고리즘은 없을까요?

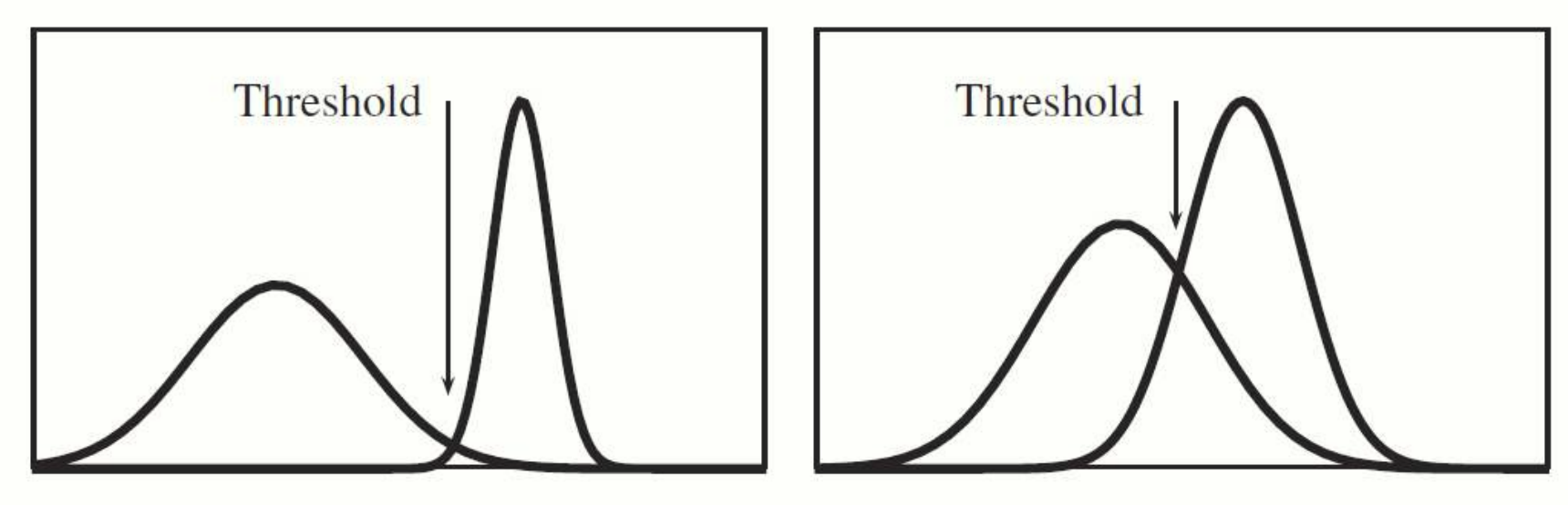
이런 히스토그램에서는 임계값을 찾기 쉽지만 모든 경우가 이렇지는 않다.

Otsu's Method

Otsu's method 가 바로 그러한 알고리즘들 중 하나입니다. 두 클래스(객체와 배경)를 효과적으로 나워야하는데, 각 클래스의 분산이 작을수록 좋습니다(즉, 클래스 내부의 값들이 서로 비슷해야 함).

방법 1)

목표: 두 클래스(객체와 배경)의 분산 합을 최소화하는 임계값 $t$ 를 찾는 것.
수식: $t = \text{argmin}_k [\omega_1(k) \cdot \text{var}_1(k) + \omega_2(k) \cdot \text{var}_2(k)]$
- $w_1(k), w_2(k)$ : 클래스 1과 클래스 2에 속하는 픽셀의 비율(가중치)
- $w_1(k) = \sum_{i=0}^{k}p_i$
- $w_2(k) = \sum_{i=k+1}^{255}p_i$
- $p_i$ : 픽셀 값의 확률 밀도 함수(PDF)
- $\text{var}_1(k), \text{var}_2(k)$ : 클래스 1과 클래스 2의 분산

이 방법은 클래스 내부 분산을 최소화하는 임계값 $t$ 을 선택합니다.

방법 2)

목표: 클래스 간 분산을 최대화하는 $t$ 를 찾는 것.
수식: $t = \text{argmax}_k [\omega_1(k) \cdot \omega_2(k) \cdot (\mu_1(k) - \mu_2(k))^2]$
- $\mu_1(k), \mu_2(k)$ : 클래스 1과 클래스 2의 평균
- $w_1(k), w_2(k)$ : 두 클래스의 가중치

이 방법은 두 클래스 간의 차이가 최대가 되는 임계값 $t$ 을 선택합니다.

구현

import skimage.filters as fl

# Otsu 임계값 계산
otsu_threshold = fl.threshold_otsu(image)

# 임계값을 이용하여 이진화 수행
binary_image = image > otsu_threshold

Otsu's Method 에 필요한 가정

히스토그램이 양봉형(bimodal)이어야 합니다.
공간적 연속성을 사용하지 않습니다. 객체의 형태나 구조를 고려하지 않으며, 오직 pixel values 만 사용합니다.
조명 변화가 적고, 객체와 배경 간의 밝기 차이가 주요 특징이어야 합니다.

Otsu's method 사용 예시.

ISODATA Method

ISODATA method 는 Iterative Self-Organizing Data Analysis Technique A 의 약자로, 반복적인 과정을 통해 최적의 임계값을 계산하는 간단하고 빠르게 수렴하는 알고리즘입니다.

과정

Step 1. 초기값 설정

정밀도 값 $\epsilon$ 과 초기 임계값 $t$ 를 설정합니다.
일반적으로 $t=\frac{L}{2}$ , 여기서 $L=256$ (그레이스케일 이미지의 pixel value 범위)

Step 2. 두 그룹의 평균 계산( $\mu_1$ 과 $\mu_2$ )

이미지 pixel values 을 기준으로 $t$ 에 따라 두 그룹으로 나눕니다.
- $\mu_1$ : 임계값 $t$ 이하의 pixel values 평균 (예: 배경)
- $\mu_2$ : 임계값 $t$ 초과의 pixel values 평균 (예: 객체)

Step 3. 새로운 임계값 계산( $t\prime$ )

두 그룹의 평균을 기반으로 새로운 임계값 $t\prime$ 를 계산합니다: $t\prime = \frac{\mu_1 + \mu_2}{2}$

Step 4. 수렴 확인

$|t - t\prime| < \epsilon$ 이면 알고리즘을 종료하고, $t\prime$ 를 최적의 임계값으로 반환합니다.
그렇지 않으면 $t$ 를 $t\prime$ 로 업데이트하고 Step 2로 돌아가 반복합니다.

구현

Step 2.

k = np.arange(256)  # pixel values 범위 (0 ~ 255)
n, _ = np.histogram(image, bins=256, range=(0, 255))  # 히스토그램 계산
p = n / image.size  # PDF 계산
wb = np.cumsum(p)  # 누적 분포 (클래스 1의 비율)
wf = 1 - wb  # 클래스 2의 비율
kpc = np.cumsum(k * p)  # 픽셀 값 누적합
mu_b = kpc / wb  # 클래스 1 평균
mu_f = (kpc[-1] - kpc) / wf  # 클래스 2 평균

Step3.

t = 128  # 초기값 설정
for i in range(10):  # 최대 10번 반복
	t1 = int((mu_f[t] + mu_b[t]) / 2.0)  # 새로운 임계값 계산
    print(t1)  # 계산된 임계값 출력
    t = t1  # 임계값 업데이트

ISODATA 의 특징

장점:

알고리즘이 간단하고 계산 속도가 빠릅니다.
데이터 분포가 명확하지 않은 경우에도 적절한 임계값을 계산할 수 있습니다.

단점:

$t$ 의 초기값 정밀도 $\epsilon$ 에 따라 수렴 속도가 달라질 수 있습니다.
반복 횟수가 많아질 경우 계산 비용이 증가할 수 있습니다.

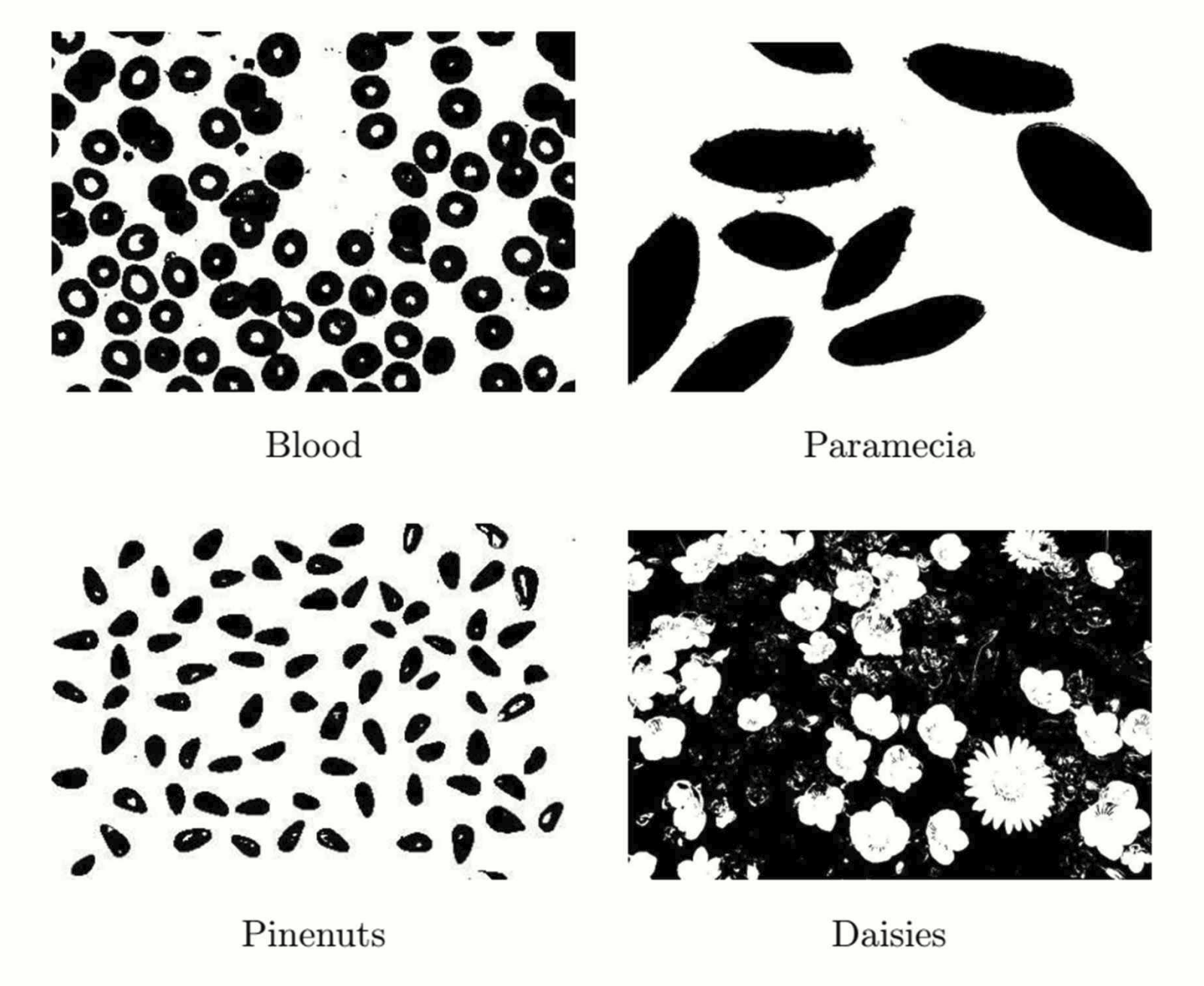
ISODATA method 결과 예시.

Adaptive Thresholding

Otsu's method 와 가은 전역(global) 임계값은 이미지 전체에 하나의 임계값을 적용합니다. 하지만 배경과 객체의 밝기가 고르지 않은(non-uniform illumination) 경우, 임계값은 효과적으로 작동하지 않을 수 있습니다. 위 figure 에서 Otsu's method 로 임계값 $t = 290.79$ 를 적용했지만, 배경 일부가 객체와 섞이는 문제가 발생했습니다. 이러한 문제를 해결하기 위해 adaptive thresholding 이 사용됩니다.

Adaptive Thresholding 이란?

이미지를 작은 블록으로 나누고, 각 블록의 특성에 따라 임계값을 개별적으로 계산합니다. 각 블록에서 최적의 임계값을 적용하므려, 비균일한 밝기 문제를 극복할 수 있습니다.

과정

Step 1. 이미지 블록화

이미지를 $n$ 개의 작은 블록으로 나눕니다.

Step 2. 블록별 임계값 계산

각 블록에 대해 Otsu's method 를 사용하여 임계값을 계산합니다.
해당 블록의 픽셀에 계산된 임계값을 적용하여 이진화합니다.

Step 3. 결과 병합

모든 블록의 이진화 결과를 결합하여 최종 이미지를 생성합니다.

구현

# 이미지의 크기 확인
r, c = image.shape

# 이미지 블록 경계 설정
starts = range(0, c-1, 162)  # 각 블록의 시작 열
ends = range(162, c+1, 162)  # 각 블록의 끝 열
z = np.zeros((r, c))  # 결과 이미지를 저장할 배열

# 각 블록에 대해 임계값 계산 및 이진화
for i in range(6):  # 총 6개의 블록
	temp = p2[:, starts[i]:ends[i]]  # 블록 추출
    z[:, strats[i]:ends[i]] = (temp > fl.threshold_otsu(temp)) * 1.0

Otsu's method 보다 나은 결과물을 얻음.

Edge Detection(1st derivatation)

이미지에서 edges 는 픽셀 값이 급격히 변화하는 부분을 의미합니다. 1차 미분은 이러한 밝기 변화의 크기와 방향을 계산하여 edges 를 검출하는 데 사용됩니다.

수학적으로 1차 미분은 다음과 같이 정의됩니다:

f{\prime}(x) = \frac{df}{dx}

이산(discrete)하게는 다음과 같이 표현할 수 있습니다:

f(x + 1) - f(x), \quad f(x) - f(x - 1), \quad \text{or } \frac{f(x + 1) - f(x - 1)}{2}

2D 이미지에서는 이를 Gradiant 로 표현합니다:

\nabla f = \left[\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right]

Gradiant 의 크기는 edge 의 세기를 나타냅니다:

\|\nabla f\| = \sqrt{\left(\frac{\partial f}{\partial x}\right)^2 + \left(\frac{\partial f}{\partial y}\right)^2}

Prewitt Filter

Prewitt filter 는 edge 검출을 위한 가장 기본적인 마스크 중 하나입니다. $P_x$ 와 $P_y$ 는 각각 가로와 세로 방향의 edge 를 검출합니다:

P_x = \begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{bmatrix}, \quad P_y = \begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{bmatrix}

구현

from skimage.filters import prewitt_h, prewitt_v

# 가로 방향 edge 검출
px = prewitt_h(image)

# 세로 방향 edge 검출
py = prewitt_v(image)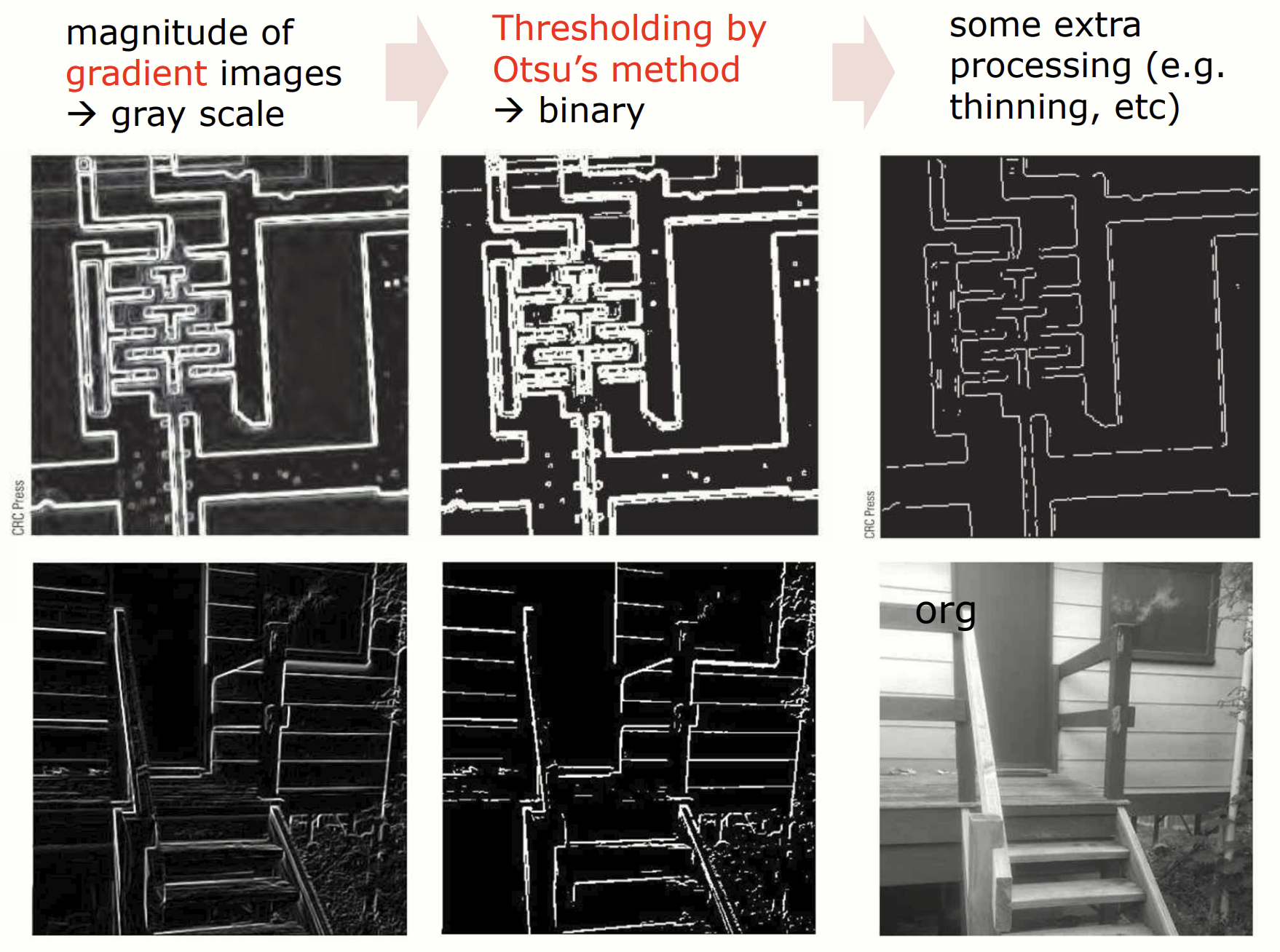

Prewitt filter 를 통해 계산된 Gradient 이미지 생성 -> Otsu's method 로 edge 를 흑백으로 분리 -> 검출된 edge 를 얇게 하거나 불필요한 noise 제거

그 외의 filters

Roberts Filter

대각선 방향의 Gradient 를 계산하는 필터입니다.

\text{Kernel 1} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}, \quad \text{Kernel 2} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}

Sobel Filter

Prewitt filter 에 비해 edge 검출 민감도를 높인 필터입니다.

\text{Sobel X} = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}, \quad \text{Sobel Y} = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}

구현

from skimage.filters import prewitt, roberts, sobel

# Prewitt 필터
edge_p = prewitt(image)

# Roberts 필터
edge_r = roberts(image)

# Sobel 필터
edge_s = sobel(image)

Edge Detection(2nd derivatation)

2차 미분 방식으로 edge detection 을 하면 회전에 대해 동일하게 동작하므로, 모든 방향에서 동일한 edges 를 검출할 수 있습니다. 하지만 2차 미분의 특성상, noise 가 증폭되기 쉽습니다.

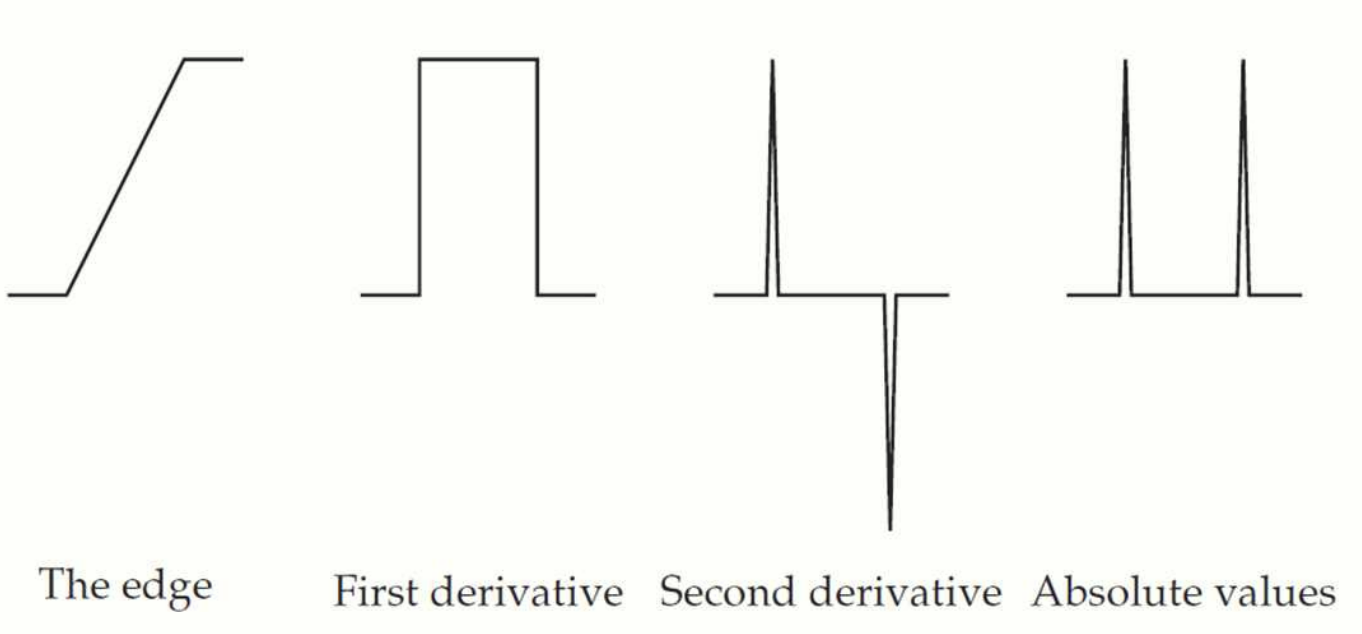
Laplacian Edge Detection

Laplacian filter 는 이미지에 2차 미분을 계산하여 edge 를 검출하는 방법입니다. 필터의 수식은 아래와 같습니다:

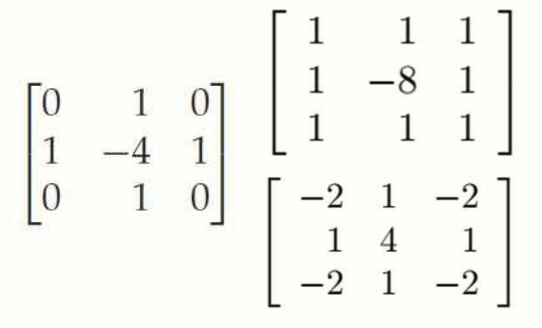
\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}

Discrete version Laplacian filter

Edge 검출 과정

필터링한 결과에서 양수에서 음수로, 혹은 음수에서 양수로 바뀌는 지점이 edge 로 간주됩니다. 이 때, Zero Crossing 을 확인하는 것이 핵심입니다.

Zero Crossing

필터의 결과값이 부호가 바뀌는 지점(양수에서 음수 또는 음수에서 양수)을 Zero Crossing 이라고 부릅니다. 한 픽셀의 8방향 이웃 픽셀들(상, 하, 좌, 우, 대각선) 을 고려하여 부호 변화를 탐색합니다.

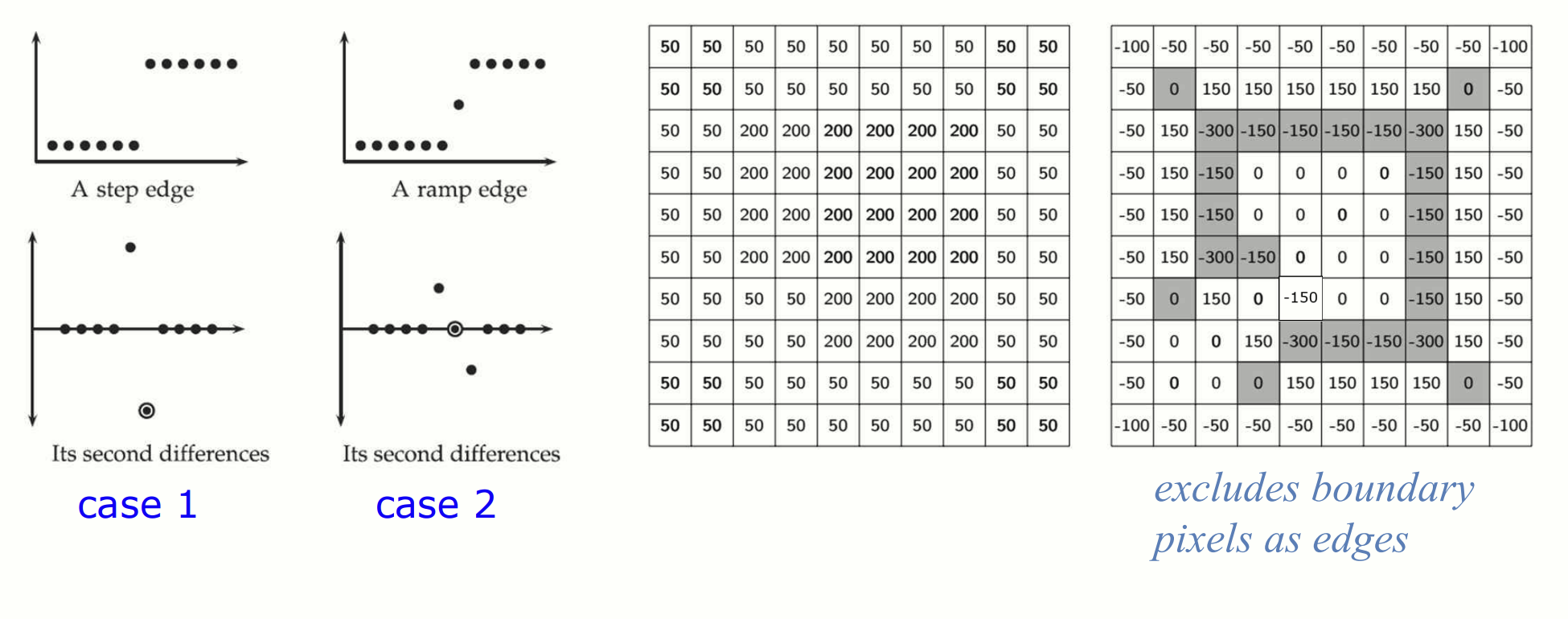
Marr-Hildreth Method

Marr-Hildreth 는 Gaussian 과 Laplacian 을 결합한 방법으로, noise 를 줄이면서 edge 를 검출하는 효과적인 기법입니다.

과정

Gaussian Filter 로 smoothing: 이미지에서 noise 를 줄이기 위해 Gaussian filter 를 적용
Laplacian Filter 적용: Edge 를 검출하기 위해 Laplacian filter 를 사용
Zero Crossing 찾기: Laplacian 결과에서 Zero Crossing 을 찾아 edge 를 결정.

구현

import numpy as np
import scipy.ndimage as ndi
from PIL import Image
def zerocross(image, threshold=0.01):
    grad_x = np.diff(image, axis=1)
    grad_y = np.diff(image, axis=0)

    zero_crossing_x = np.abs(grad_x) > threshold
    zero_crossing_y = np.abs(grad_y) > threshold

    zero_crossings = np.zeros_like(image, dtype=bool)
    zero_crossings[:, :-1] |= zero_crossing_x
    zero_crossings[:-1, :] |= zero_crossing_y

    return zero_crossings.astype(np.uint8) * 255

image = np.array(Image.open(circuit.png))
s2 = ndi.gaussian_laplace(np.float64(image), sigma=3)
s_edge = zerocross(s2)

Canny Edge Detector

Canny Edge Detector 는 가장 널리 사용되는 edge detector 알고리즘 중 하나로, 1986년 John Canny 에 의해 제안되었습니다. 이 알고리즘은 세 가지 주요 단계로 구성됩니다.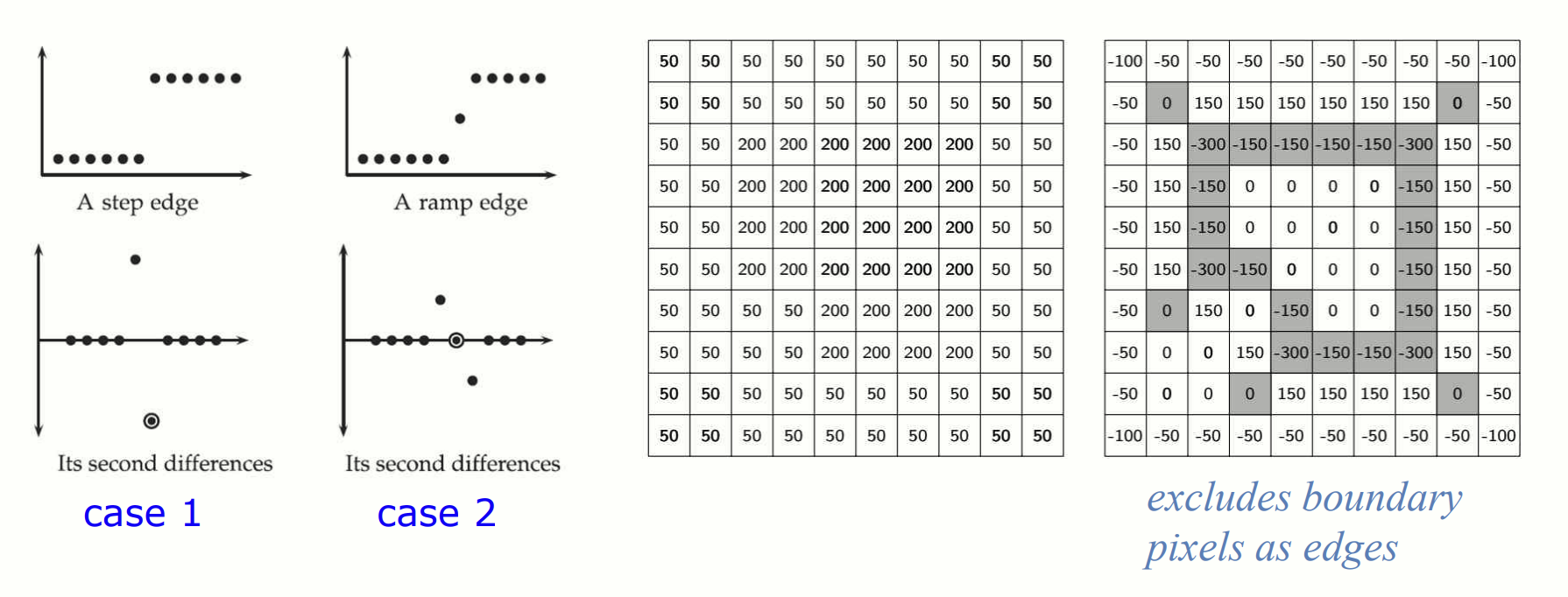

Canny Edge Detector 과정

Step 1. 1D DoG Filter 적용(edge 강도 계산)

모든 가능한 edge 를 검출하며 noise 를 억제합니다.

1D Gaussian Filter $g$ 생성: noise 를 줄이기 위해 이미지를 smoothing
Gaussian 의 1차 미분 필터 $dg$ 생성: Edge 근처의 픽셀 간 변화(Gradient)를 강조
$dg$ 를 $x$ 에 적용하여 수평 방향 결과 $x1$ 을 얻음.
$dg.T$ 를 $x$ 에 적용하여 수직 방향 결과 $x2$ 를 얻음.
$x1$ 과 $x2$ 를 사용하여 edge 강도 $xe$ 를 계산:
$xe = \sqrt{x1^2 + x2^2}$

Step 2. Non-Maxima Suppression (edge 얇게 만들기)

검출된 edge 의 폭을 얇게(thinning) 만들어 edge 의 정확도를 높입니다. 같은 방향으로 뻗은 edge 들 중 단 한 개의 edge 만 남기고 나머지는 제거하는 방식입니다. 이것을 구현하기 위해 미분 결과의 최고값만을 남기고 어중간한 값들은 배제합니다. 이 과정은 thresholding 만으로는 정교하게 수행될 수 없기에 다음과 같은 과정을 거칩니다.

$x1, x2$ 로부터 edge normal vector( $xg$ ) 계산: $xg = \tan^{-1}\left(\frac{x2}{x1}\right)$

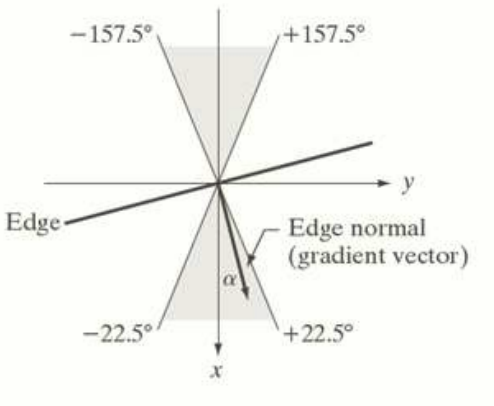
Edge 의 법선 벡터가 xg 라고 생각하면 편하다.

Edge normal vector $xg$ 를 8방으로 양자화합니다. 양자화된 방향으로 양 옆의 두 픽셀에 대한 $xg$ 를 계산합니다. 이들 중 한 픽셀이라도 더 큰 값의 $xg$ 가 있으면 현재 픽셀을 edge 에서 탈락시킵니다. 같은 방향성을 가진 edges 중 강력한(dominant) edge 만을 추려내어 최종 edge 영상을 구합니다.

각 픽셀에서 $xe[x, y]$ 가 이웃 픽셀 중 하나라도 작으면 억제(0으로 설정)합니다. 즉, 2 의 결과를 강력한 edge 영상과 약한 edge 영상으로 분리하고, 강한 edge 영상과 연결된 약한 edge 영상 픽셀이 있으면 이들을 강한 edge 영상에 포함시키고 아니면 없애버립니다.

Step 3. Hysteresis Thresholding (약한 edge 연결)

강한 edge 를 기준으로 약한 edge 를 연결하여 edge 를 더욱 안정적으로 확장시킵니다. 이 과정에서 두 개의 임계값 $T_L$ (낮은 임계값), $T_H$ (높은 임계값)을 사용합니다.

$g_{NH}[x, y] : xe[x, y] \geq T_H$ 인 강한 edge
$g_{NL}[x, y] : xe[x, y] \geq T_L$ 인 약한 edge
약한 edge 가 강한 edge 에 연결되면 edge 로 간주, 그렇지 않으면 제거

Canny 함수

skimage.feature.canny(image, sigma=1.0, low_threshold=None, highthreshold=None, mask=None, use_quantiles=False, *, mode='constant', cval=0.0)```

sigma:
- Gaussian filter 의 표준 편차(standard deviation)
- Image smoothing 에 사용되며, noise 를 줄이고 더 부드러운 edge 를 검출
- 기본값은 1.0
low_threshold:
- Hysteresis thresholding 의 하한값
- 연결된 edge 를 찾는 과정에서 weak edge 를 포함할지 결정
- 기본값은 데이터 타입의 최대값의 10%
high_threshold:
- Hysteresis thresholding 의 상한값
- Strong edge 를 검출하는 기준
- 기본값은 데이터 타입의 최대값의 20%

구현

import cv2  # OpenCV 패키지
import skimage.feature as sf

edges = cv2.Canny(image, threshold1=50, threshold2=150)
edges2 = sf.canny(image)

threhold2 를 높게 설정하면 더 적은 edge 가 검출되고, 낮게 설정하면 더 많은 edge 가 검출됩니다.

Edge 를 얇게 살려 깔끔한 outline 을 구함.

Hough Transform

이미지 내의 가장 지배적인(dominant) 직선을 segmentation 하고 싶다면 Hough transform 을 사용합니다. Hough transform 의 기본적인 철학은 점을 선으로 변환한다는 것입니다. Canny detector 같은 과정을 미리 거친 다음, binary 영상에서 직선을 찾는 것입니다.

직선의 방정식을 이용한 Hough Transform

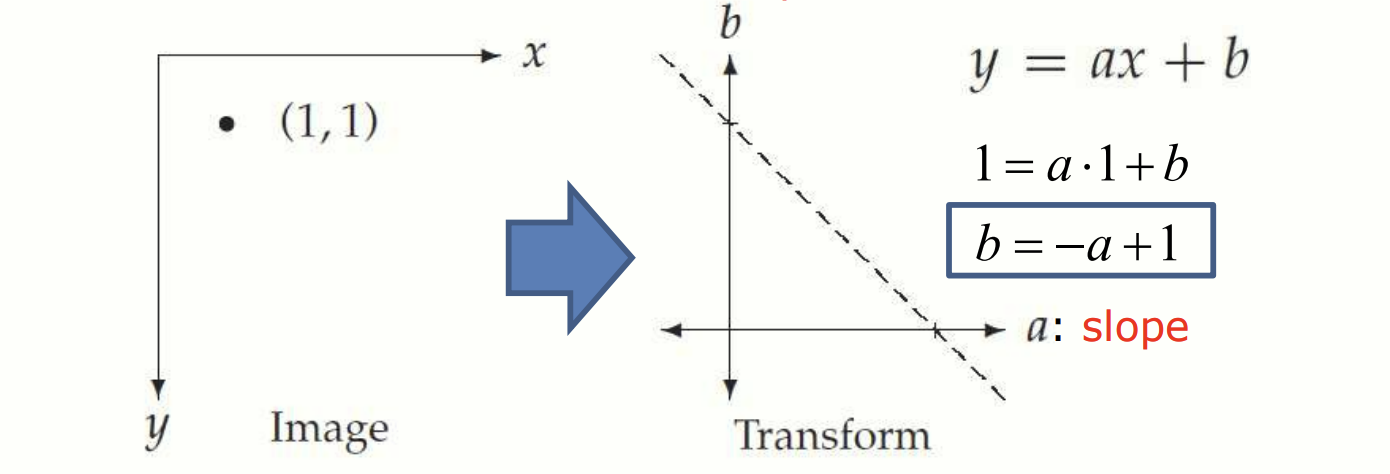
좌표를 안다면 y = ax + b 에 대입하여 ab 좌표에 직선을 그릴 수 있다.

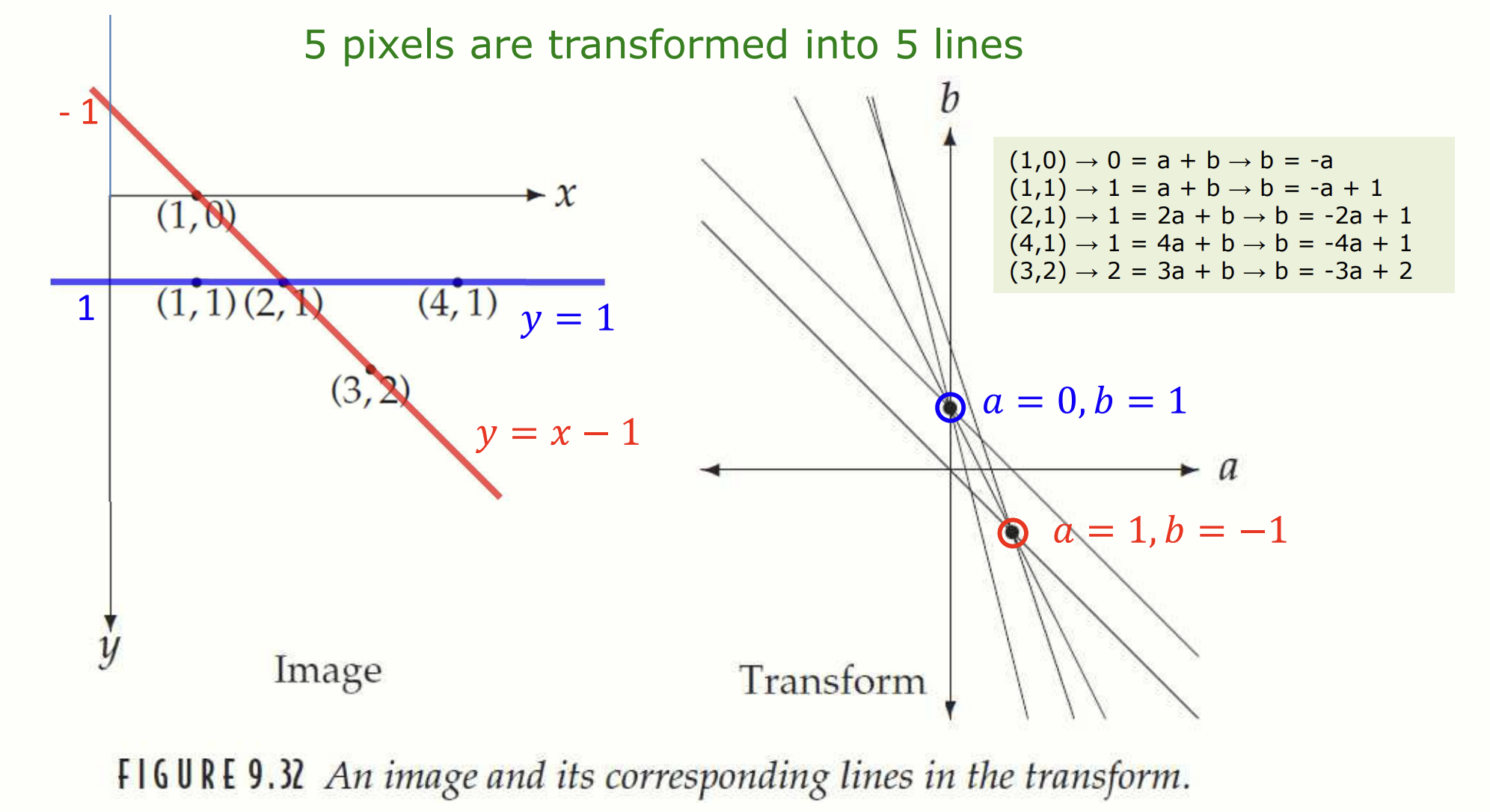
위의 figure 를 해석해봅시다. 우리는 이미지의 다섯 개의 좌표를 알고 있습니다. 이 좌표들을 $ab$ 좌표평면으로 옮겨서 다섯 개의 직선을 그렸습니다. 가장 많은 직선이 지나가는 교점은 ( $a=0, b=1$ ), ( $a=1, b=-1$ ) 입니다. 이 점을 다시 $xy$ 좌표평면으로 옮기면 $y=1$ , $y=x-1$ 직선을 얻을 수 있습니다. 과연 이 직선들은 세 점이 지나가는, 즉 가장 많은 점이 지나가는 직선이군요! 이로서 우리는 이미지에서 가장 지배적인(dominant) 두 가지 직선을 알아냈습니다.

극좌표를 이용한 Hough Transform

다만 기울기가 무한대일 경우 문제가 생길 수 있습니다. 이를 해결하기 위해 극좌표를 사용합니다.

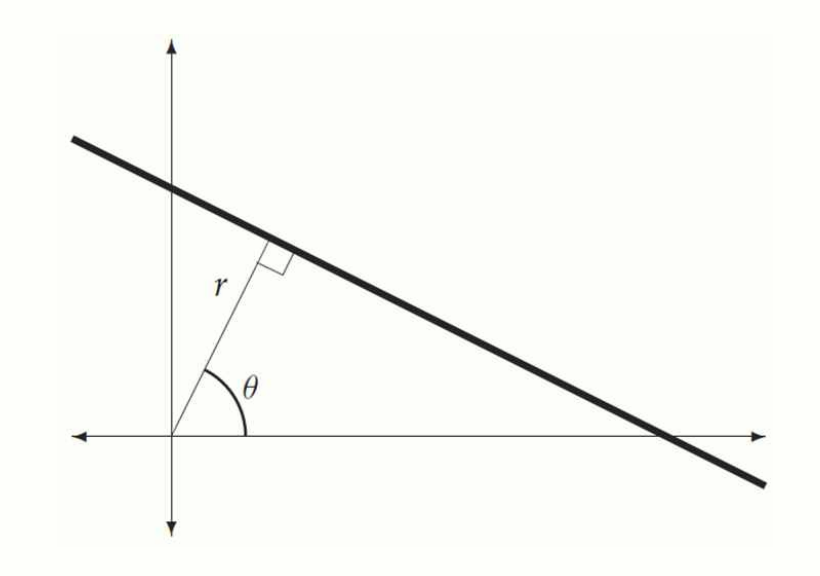
직선을 극좌표 방정식으로 나타내면 다음과 같습니다:

r = x\cos\theta + y\sin\theta

$r$ : 직선과 원점 사이의 수직 거리
$\theta$ : 직선과 $x$ 축의 수직선이 이루는 각도
$\theta$ 는 $0^\circ$ 에서 $180^\circ$ 사이의 값

이 방식은 모든 직선을 표현할 수 있으며, 특히 수직선도 다룰 수 있습니다. Hough transform 은 이미지의 각 픽셀에 대해 모든 가능한 $r$ 과 $\theta$ 값을 계산합니다. 극좌표 변환 결과가 히스토그램에서 높은 값이라면 그 직선을 따라 더 많은 픽셀이 존재한다는 의미입니다. 즉, 해당 $r$ , $\theta$ 값이 강한 직선을 나타낸다는 것입니다.

극좌표를 이용한 Hough Transform 계산 방법.

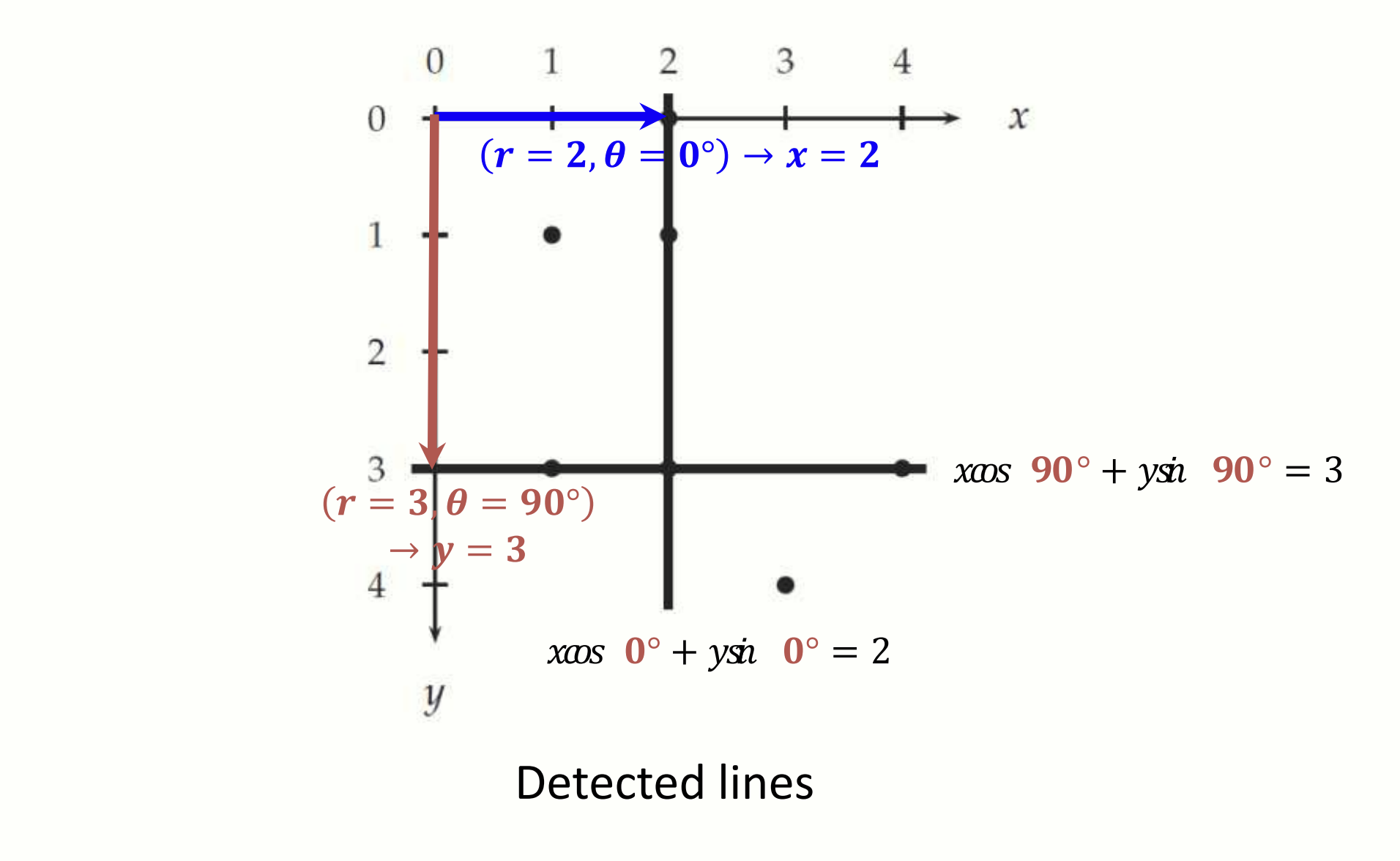
검출된 직선들.

구현

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
# Canny Edge Detector 로 이미지에서 edge 를 검출
from skimage.feature import canny
# hough_line: Hough Transform 을 수행하여 edge 에서 직선의 파라미터(각도와 거리)를 계산한다
# hough_line_peaks: Hough 공간에서 강도가 높은, 즉 두드러진 직선만 추출한다
from skimage.transform import hough_line, hough_line_peaks

def draw_houghlines(image, angles_peaks, dists_peaks):
	plt.figure()
    plt.imshow(image, cmap='gray')
    plt.title('Detected Lines')
    # 입력 이미지를 회색조로 출력하여 직선을 그릴 준비
    for angle, dist in zip(angles_peaks, dists_peaks):
    	x0 = 0; x1 = image.shape[1]
        y0 = (dist - x0 * np.cos(angle)) / np.sin(angle)
        y1 = (dist - x1 * np.cos(angle)) / np.sin(angle)
        plt.plot((x0, x1), (y0, y1), '-r')  # Draw lines in red
    # Hough Transform 의 결과(각도와 거리)를 사용하여 직선 방정식 구하기
    plt.xlim(0, x1)
    plt.ylim(image.shape[0], 0)
    plt.show()

# 이미지 불러오기
image = np.array(Image.open('skull.png').convert('L'))
# Hough Transform 적용
edges = canny(image)
hspace, angles, distances = hough_line(edges)  # hspace: Hough 공간의 누적 결과(강도), angles: 직선의 각도 값 배열, distances: 직선의 거리 값 배열
accum, angles_peaks, dists_peaks = hough_line_peaks(hspace, angles, distances, num_peaks=10)  # angles_peaks: 가장 강한 직선들의 각도, dists_peaks: 가장 강한 직선들의 거리

# 입력 이미지에 Hough lines 그리기
draw_houghlines(image, angles_peaks, dists_peaks)

파워

개발자 준비생

이전 포스트

Image Restoration

다음 포스트