이번 장에서는 형상(Shape)과 객체의 경계(Boundary)를 표현하고 분석하는 방법에 대해 알아봅시다.

형상 분석의 목적

• 형상 비교: 두 객체가 동일한 모양을 가졌는지 어떻게 판단할 것인가?

• 형상 분류: 서로 다른 객체들을 모양에 따라 어떻게 분류할 것인가?

• 형상 설명: 한 객체의 모양을 어떻게 효과적으로 설명할 것인가?

Chain Code

---

Chain Code 는 객체의 경계를 따라 움직이면서 각 방향을 기록하는 방법입니다.

방법:

1. 객체의 경계를 따라 이동합니다.

2. 이동하는 방향(direction)으르 숫자로 기록합니다.

3. 방향의 리스트가 곧 Chain Code 가 됩니다.

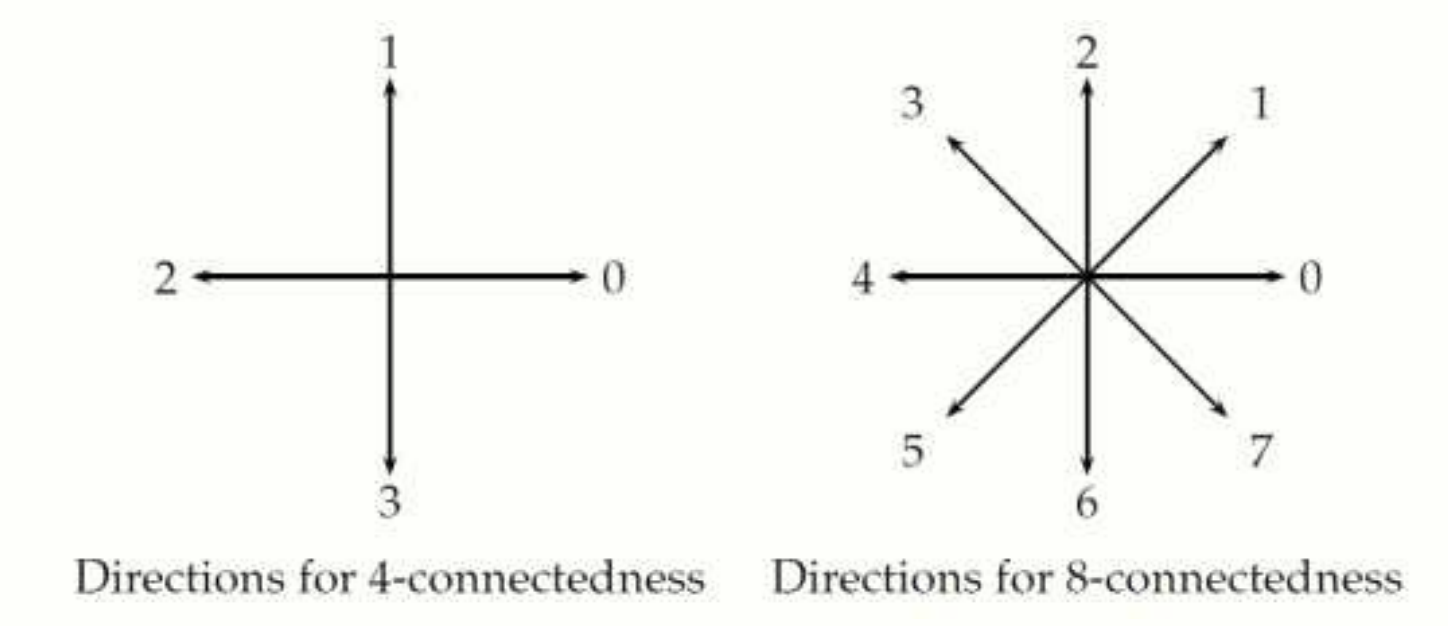
Freeman Chain Code.

Chain Code 사용례

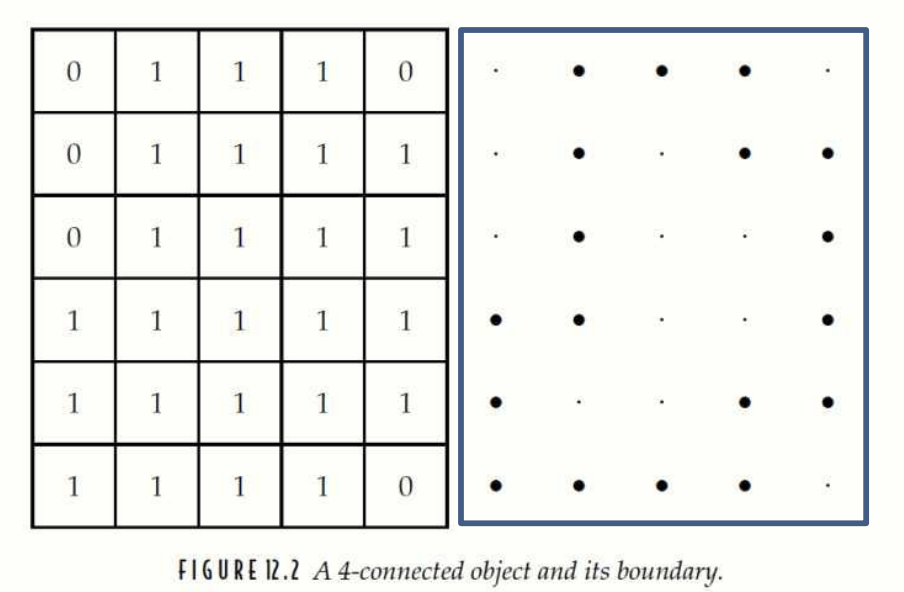
객체의 경계(주어진 이미지에서 1의 경계선)를 반시계 방향으로 따라갑니다.

각 이동 방향을 숫자로 기록합니다. 위 figure 에서는 Freeman chain code 를 사용했습니다.

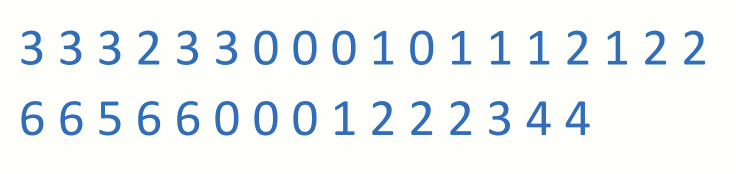
주어진 객체를 따라 움직이면 위와 같은 chain code 를 얻게 됩니다.

Chain Code 의 문제점

Chain code 를 단순히 객체의 경계를 따라 방향을 기록하는 방식으로 사용할 경우, 다음과 같은 두 가지 문제가 발생합니다:

1. 시작 픽셀(Starting Pixel)에 의존적

• Chain code 는 경계를 기록할 때 출발점을 기준으로 기록하므로, 동일한 객체라도 출발점이 다르면 다른 chain code 로 나타날 수 있습니다.

2. 객체의 방향(Orientation)에 의존적

• 객체가 회전하거나 대칭적으로 변형되면 chain code 도 함께 변합니다.

• 이러한 특성 때문에 회전이나 대칭에 대한 정규화(Rotation Normalization)가 필요합니다.

First Difference of Chain Codes

---

Chain code 의 문제점들을 해결하기 위해, First Difference(1차 미분) 방식을 사용합니다. 이 방법은 방향성 정보를 차분하여 상대적인 방향만 기록하므로, 출발점이나 회전에 덜 민감합니다.

두 인접한 chain code 요소 간의 방향 차이를 기록하는데, 이 방향 차이는 반시계 방향(counter-clockwise)을 기준으로 계산됩니다.

위와 같은 chain code 를 기준으로 반시계 방향의 차이를 계산한다.

계산 과정

1. Chain code 의 두 인접 요소 간 방향 차이를 계산합니다. 예를 들어:

   • Chain code: 10103322

   • 방향 차이(1차 미분): 3133030

2. 마지막 요소와 첫 번째 요소 간의 방향 차이도 계산하여, 리스트 맨 앞에 추가합니다.

   • 마지막과 첫 번째 방향 차이: 2 -> 1 = 3

   • 최종 결과: 33133030

Shape Number

---

First Difference Chain Code 도 한계는 분명히 존재합니다. 이 방식은 경계가 회전이나 크기에 대해 완전히 불변하지 않을 수도 있습니다. 현실에서는 객체의 방향이나 크기가 바뀌는 경우가 많아, 더 나은 방식이 필요할 수 있습니다. 그 대안이 바로 Shape Number 입니다.

Shape number 는 객체의 방향에 독립적이며, 객체의 고유한 모양을 나타내는 숫자입니다.

정의

Shape number 는 chain code 의 first difference 를 순환적으로 이동(circular shifting)하여, 가장 작은 값이 되도록 만든 결과입니다.

계산 과정

1. Chain Code 에서 First Difference 계산

• 예: Chain Code 10103322

• First Difference: 33133030

2. 순환 이동(Circular Shifting)

• First Difference 값을 원형으로 이동하면서, 전체적으로 가장 작은 값을 찾습니다.

• 예: 33133030 -> 이동 -> 03033133 (가장 작은 값)

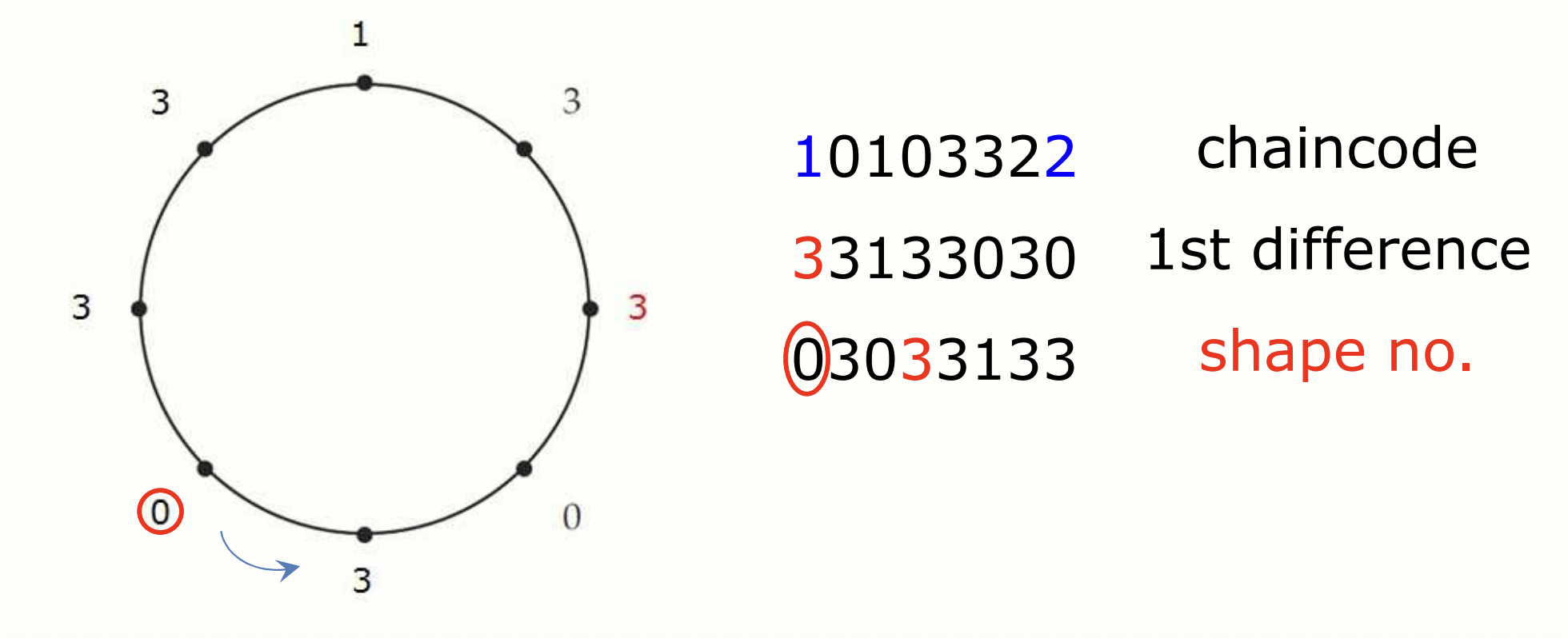
예시

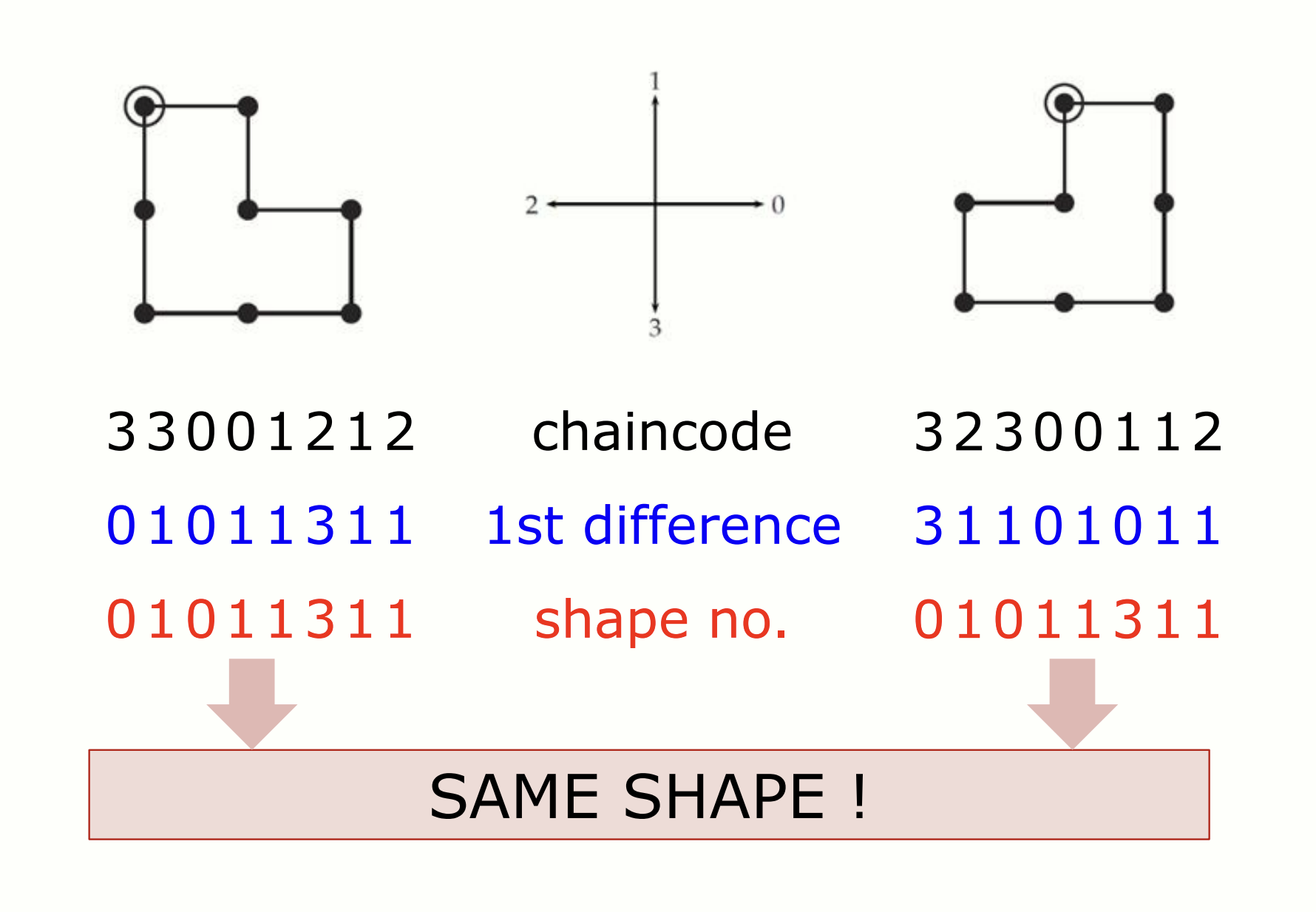
두 shape 은 서로 rotation 시키면 동치시킬 수 있습니다. 만약 1st difference chain code 로 표현하면 둘은 서로 결과값이 다르지만, shape number 로 표현하면 둘은 서로 결과값이 같습니다.

Fourier Descriptors

---

Fourier Descriptors(FD) 는 물체의 외곽선 정보를 표현하고 분석하기 위한 방법 중 하나입니다.

• Chain Code 처럼 방향만 기록하게 아니라, 경계 좌표(boundary coordinates)를 복소수(Complex Numbers)로 변환하여 사용합니다.

• 복소수 $z = x + yi$ : $x$ 는 실수부(Real), $y$ 는 허수부(Imaginary)를 나타냅니다.

• 경계 좌표 리스트에 대해 푸리에 변환을 수행하면, 이 결과를 Fourier Descriptor로 정의합니다.

프로세스

1. 경계 좌표를 복소수로 변환: 경계에 있는 각 픽셀의 좌표 $(x, y)$ 를 복소수 $z = x + yi$ 로 표현

2. 푸리에 변환: $z$ 리스트에 대해 numpy.fft.fft() 을 수행하여 푸리에 계수를 얻음

3. 고주파 성분 제거: 관심이 없는 세부 정보(고주파 성분)를 제거하여 데이터 크기를 줄임

4. 역푸리에 변환: numpy.fft.ifft() 를 사용하여 데이터를 복원. 이때 제거된 고주파 성분으로 인해 단순화된 물체 외곽선을 얻을 수 있음.

예시

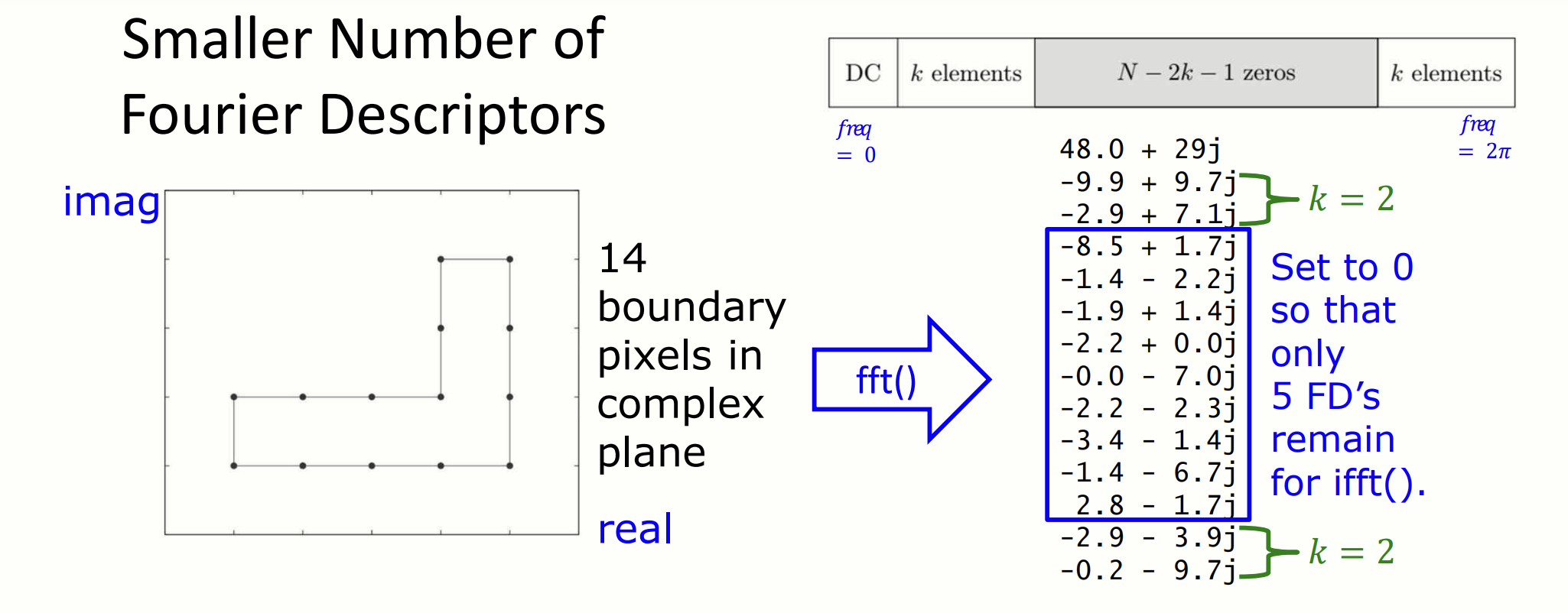
imag 경계의 14개 점을 복소수 좌표로 변환한 후, 푸리에 변환을 수행합니다. $k=2$ 일 때, 5개의 FD 만 남기고 나머지는 0으로 설정한 뒤 역변환합니다($k$ 를 늘릴수록 점점 원래 외곽선에 가까워집니다).

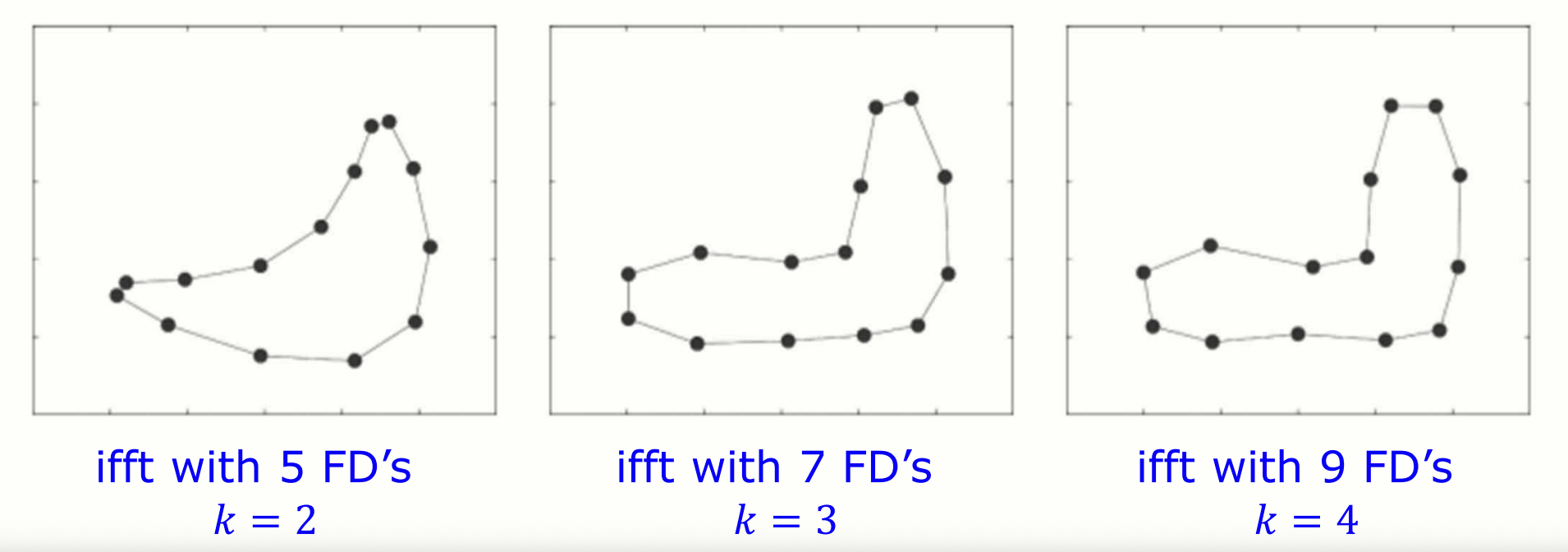
장점

1. 데이터 축소

• Boundary 의 픽셀이 굉장히 많은 복잡한 형태를 단 몇 번의 FD 로 요약이 가능합니다.

• 데이터의 크기가 줄어들면서 계산 효율성이 크게 향상됩니다.

2. 전역 특성 유지

• 디테일한 경계 정보가 사라져도 크기, 대칭성 등 전역 특성이 보존되는 편입니다.

• 이는 물체를 분류하거나 비교할 때 매우 유용합니다.

3. 유연성

• $k$ 값을 조절하여 원하는 수준의 세부 정보와 단순화된 데이터를 얻을 수 있습니다.

• 예를 들어, $k = 8$ 일 때는 단순화된 외곽선, $k = 32$ 일 때는 더 세밀한 외곽선을 보입니다.

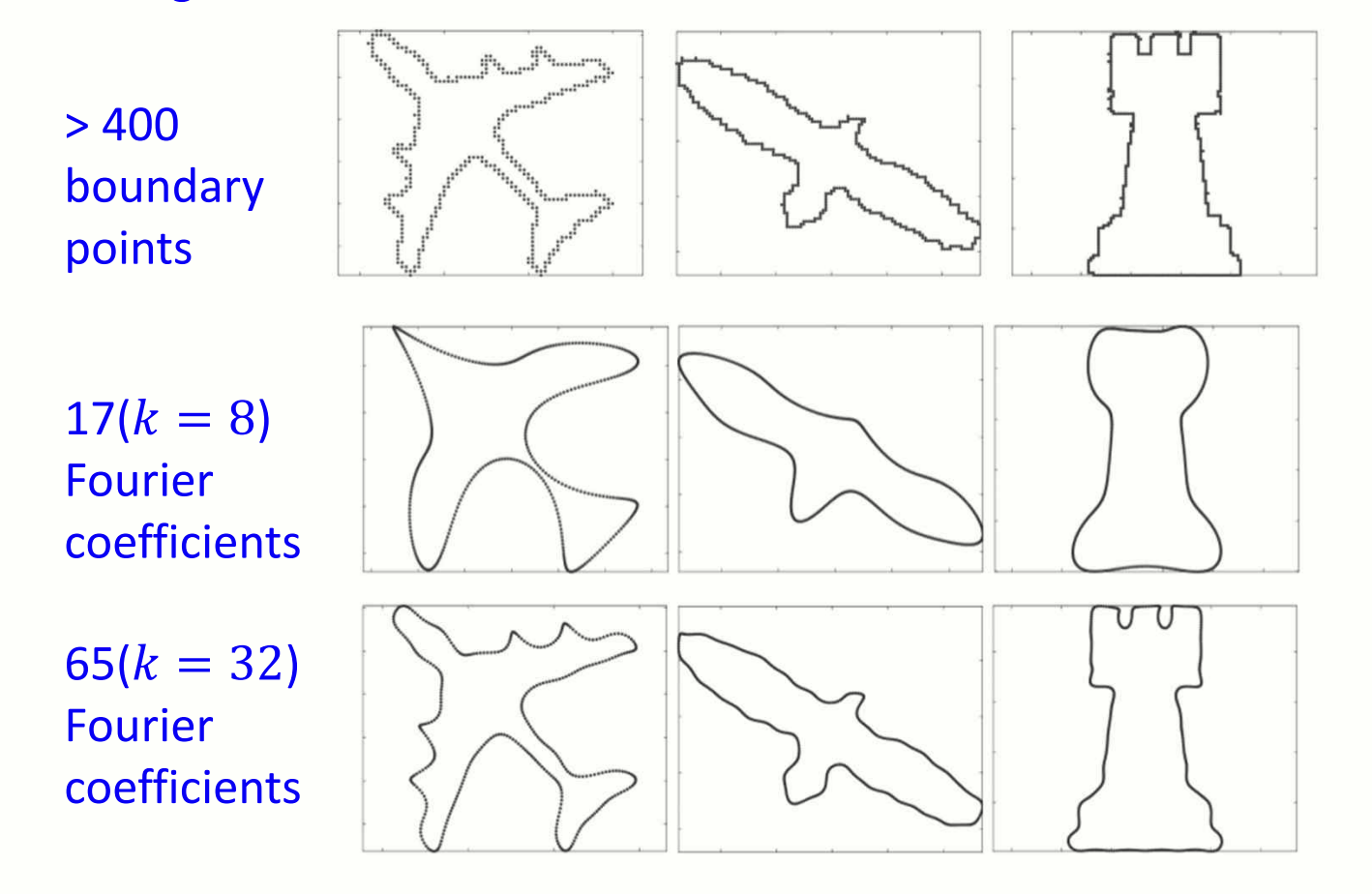
첫 번째 줄의 사진들은 매우 복잡한 디테일이 포함된 경계(>400개의 경계 점)를 가진 원본 이미지들입니다. 이러한 데이터를 처리하려면 저장 공간과 계산 리소스가 많이 필요합니다.

두 번째 줄의 사진들은 8개의 FD 만 사용하여 단순화된 외곽선을 생성한 것입니다. 일부 디테일은 사라지지만, 물체의 전반적인 모양(전역적 특성)은 유지됩니다.

세 번째 줄의 사진들은 32개의 FD 를 사용하여 더 많은 디테일이 포함된 외곽선을 생선한 것입니다.원본 경계선과 유사하며 여전지 전역적인 특성은 유지됩니다.