Introduction

---

Image Topology 란?

디지털 이미지를 분석할 때, 주로 객체의 기본 속성에 관심을 가집니다. 예를 들어:

• 특정 객체가 등장하는 빈도
• 이미지에 구멍이 있는지 여부 등

이러한 이미지의 근본적인 속성을 분석하는 것을 Digital Topology 또는 Image Topology 라고 합니다. 이는 픽셀의 배치나 구성의 관점에서 바라보는 개념입니다.

Neighbor and Adjacency

어떤 조건에서 픽셀이 다른 픽셀과 인접하다고 할 수 있을까요? 이번 장에서는 binary image 를 기준으로, 픽셀의 위치 만 고려합니다.

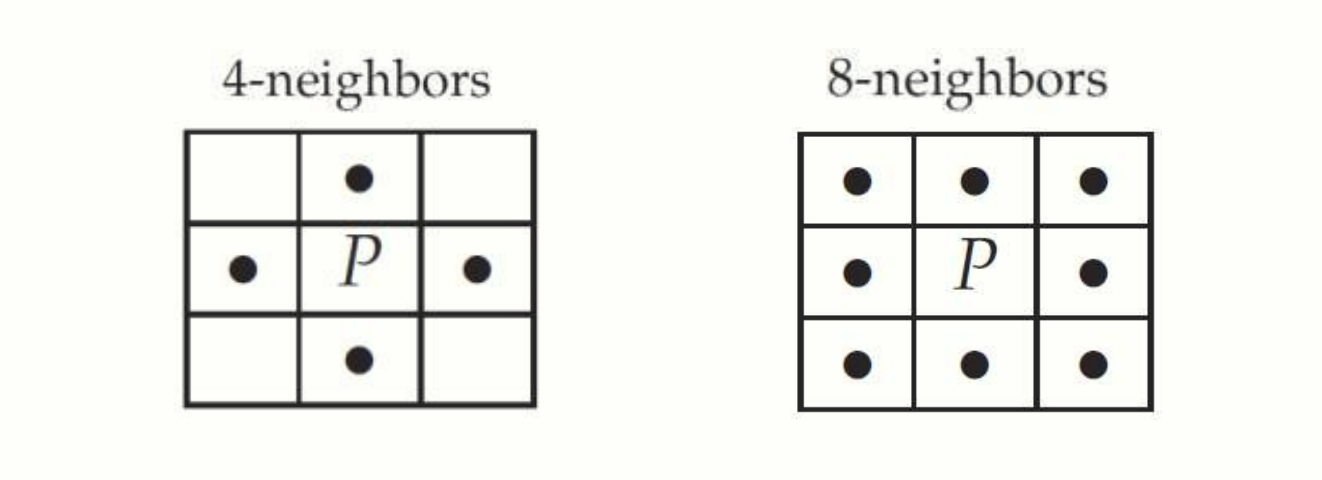
Morphology 에서 다뤘듯이 인접한 픽셀을 이야기할 때는 4-neighbors, 8-neighbors 로 표현합니다. 픽셀 P와 Q가 4-neighbors 이나 8-neighbors 이면, 각각 4-adjacent 또는 8-adjacent 이라고 합니다.

Paths and Components

두 픽셀 P 와 Q 가 연결되어 있는지를 확인하는 방법은 다음과 같습니다:

• 4-connected: P 와 Q 를 연결하는 경로가 오직 4-adjacent 인 픽셀로만 구성된 경우
• 8-connected: P 와 Q 를 연결하는 경로가 8-adjacent 인 픽셀로만 구성된 경우

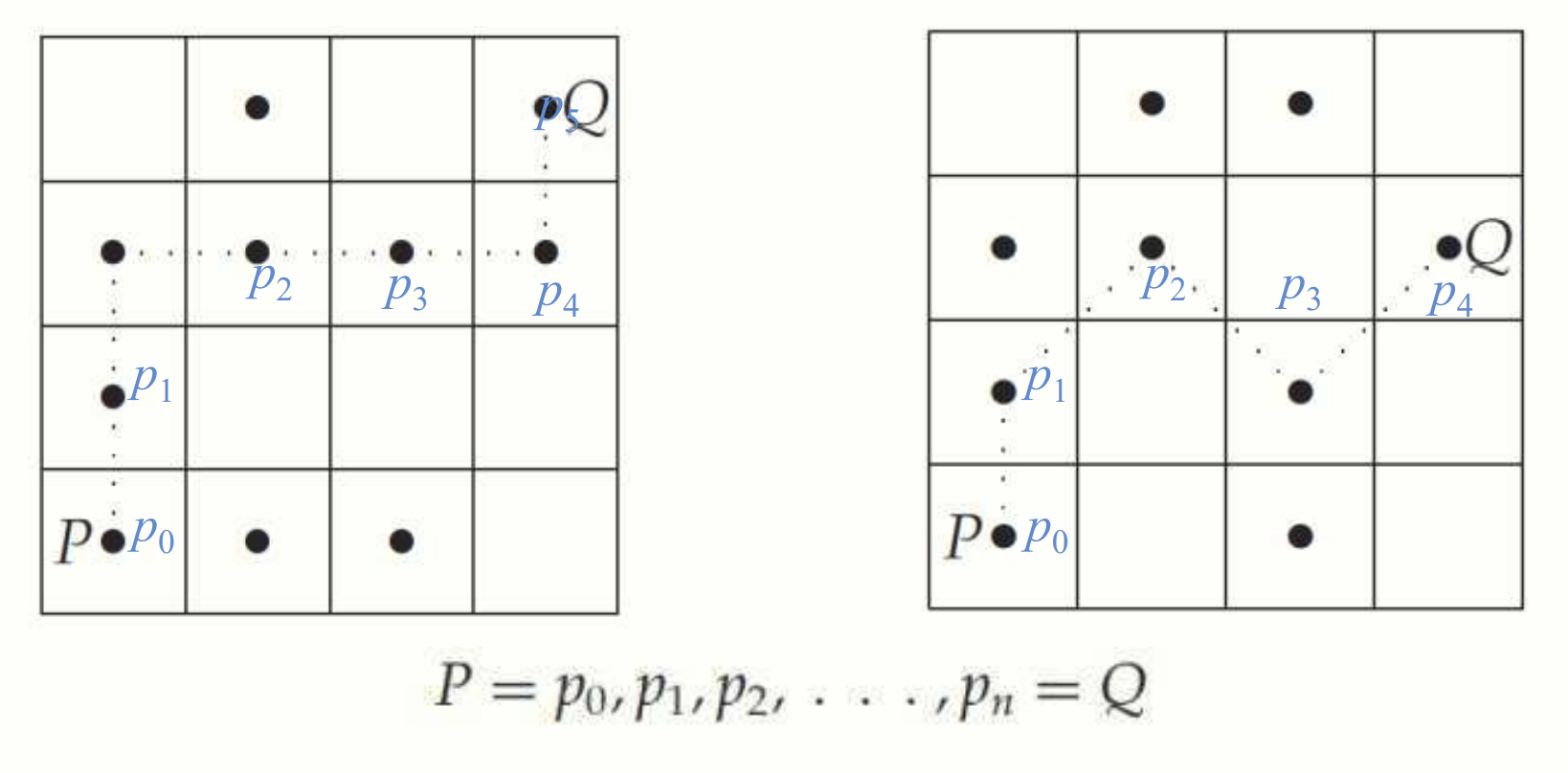
왼쪽의 P 와 Q 는 4-connected, 오른쪽의 P 와 Q 는 8-connected

Component:

• 4-component: 서로 4-connected 된 픽셀 집합
• 8-component: 서로 8-connected 된 픽셀 집합

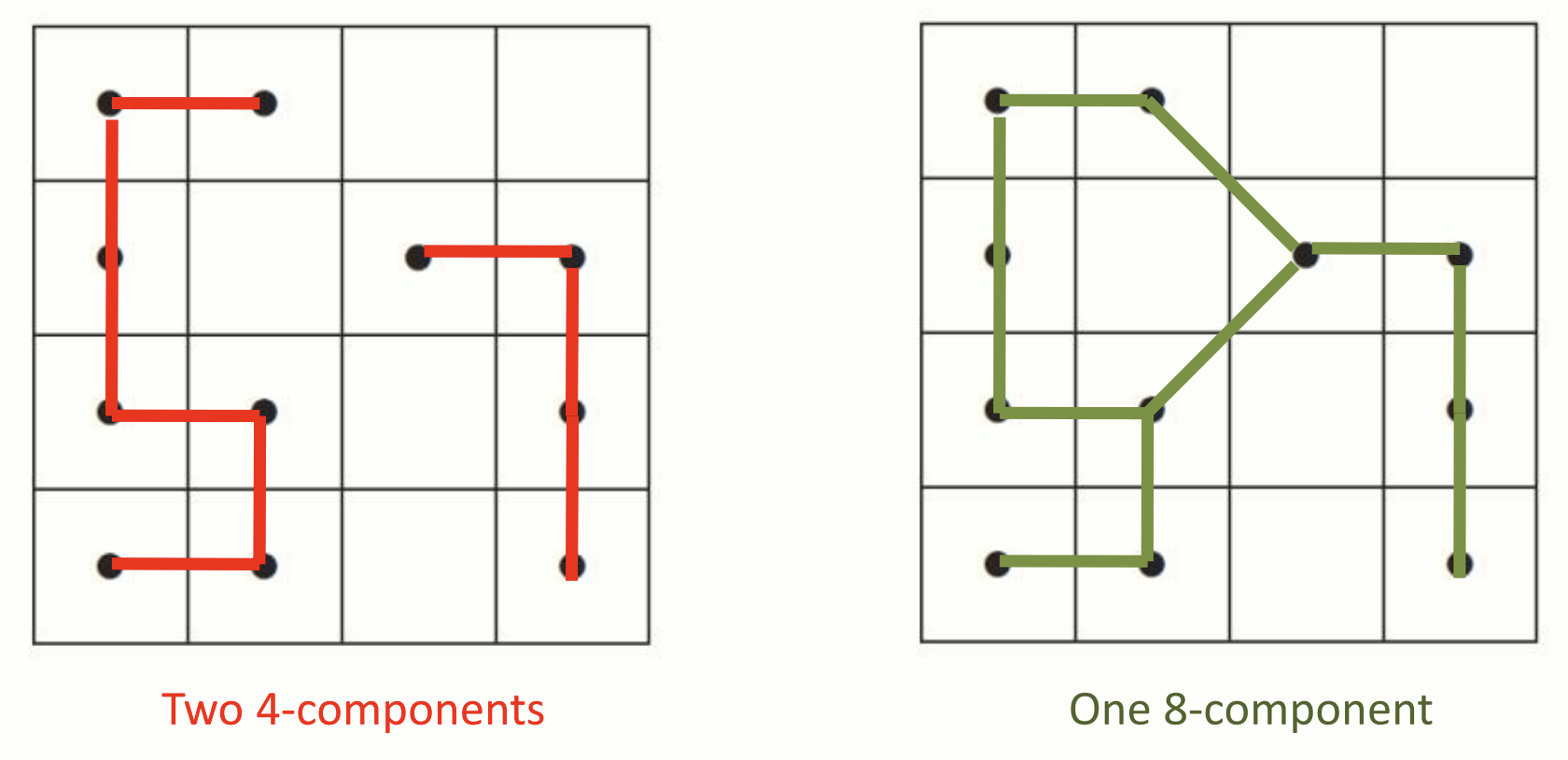
Equivalence Relations (동치 관계)

~ 는 equivalence relation 를 나타내는 기호입니다. 이를 통해 두 객체가 어떤 조건에서 같은 클래스(equivalence class)에 속하는지를 표현합니다.

수학적으로, 모든 $x$ 에 대해 $x \sim x$ 를 만족해야 합니다. 즉, $x$ 는 항상 자기 자신과 동치입니다. 이를 반사성이라고 합니다.

$x \sim y$ 가 성립하면, $y \sim x$ 도 성립해야 합니다. 즉, $x$ 와 $y$ 가 동치라면, 관계의 방향이 바뀌어도 동치입니다. 이를 대칭성이라고 합니다.

$x \sim y$, $y \sim z$ 라면 $x \sim z$ 가 성립해야 합니다. 즉, $x$ 와 $y$, $y$ 와 $z$ 가 각각 동치라면, $x$ 와 $z$ 도 동치입니다. 이를 추이성이라고 합니다.

예시

수적 동치: $x \sim y$ 는 $x=y$ 일 때 성립합니다.
예: $5\sim5$

약수(Divisors)에 따른 동치: $x \sim y$ 는 $x$ 와 $y$ 를 같은 숫자로 나눌 때 나머지가 동일하면 성립합니다.
예: $10 \sim 4$ (모듈로 3에서 10%3 = 4%3 = 1)

Connected component: 이미지 분석에서 $P \sim Q$ 는 $P$ 와 $Q$ 가 같은 connected component 에 포함되어 있을 때 성립합니다.
예: 두 픽셀이 4-connected 또는 8-connected 로 연결되어 있으면 동치 관계로 봅니다.

Equivalence Class 는 동치 관계에 의해 묶인 객체들의 집합입니다. 즉, $x \sim y$ 를 만족하는 모든 $x$ 와 $y$ 는 같은 클래스에 속합니다.

Component Labeling

---

Component labeling 은 binary image 에서 connected components 를 식별하고, 각 그룹에 고유한 라벨을 부여하는 과정을 말합니다.

기본 용어

• Foreground pixel (fg): 이미지 내 객체를 나타내는 픽셀(값이 1인 픽셀)

• Background pixel (bg): 이미지에서 객체가 아닌 영역(값이 0인 픽셀)

과정

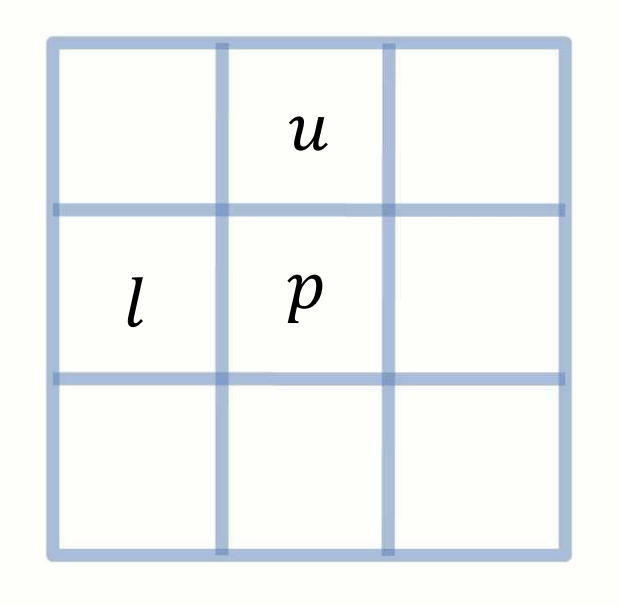
Step 1: 현재 픽셀의 상태 확인

• $p$ : 현재 확인 중인 픽셀
• $u$ : $p$ 의 위쪽 픽셀
• $l$ : $p$ 의 왼쪽 픽셀

$p$ 가 Foreground 픽셀($p=1$)인 경우: $u$ 와 $l$ 의 상태에 따라 아래와 같이 처리합니다:

• $u$ 와 $l$ 이 Background 픽셀(0)이면: $p$ 에 새로운 라벨을 할당합니다.

• $u$ 또는 $l$ 중 하나가 Foreground 픽셀이면: 해당 라벨을 $p$ 에 할당합니다.

• $u$ 와 $l$이 Foreground 픽셀이며, 같은 라벨을 가진 경우: $p$ 와 동일한 라벨을 할당합니다.

• $u$ 와 $l$ 이 Foreground 픽셀이지만, 서로 다른 라벨을 가진 경우: $p$ 에 둘 중 하나의 라벨을 할당하고, 두 라벨이 동치 관계(equivalence)라는 메모를 추가합니다. 이는 $u$ 와 $l$ 이 $p$ 를 통해 같은 connected component 에 속함을 의미합니다.

Step 2: 라벨 정렬

라벨 간의 동치 관계를 바탕으로, 모든 라벨을 동치 클래스(Equivalence Class)로 묶습니다. 각 클래스에 새로운 라벨을 할당합니다.

Step 3: 라벨 대체

모든 Foreground 픽셀에 대해, Step 2 에서 정의한 동치 클래스의 라벨로 기존 라벨을 대체합니다.

참고: 8-components 에서는 다음과 같이 labeling 합니다.

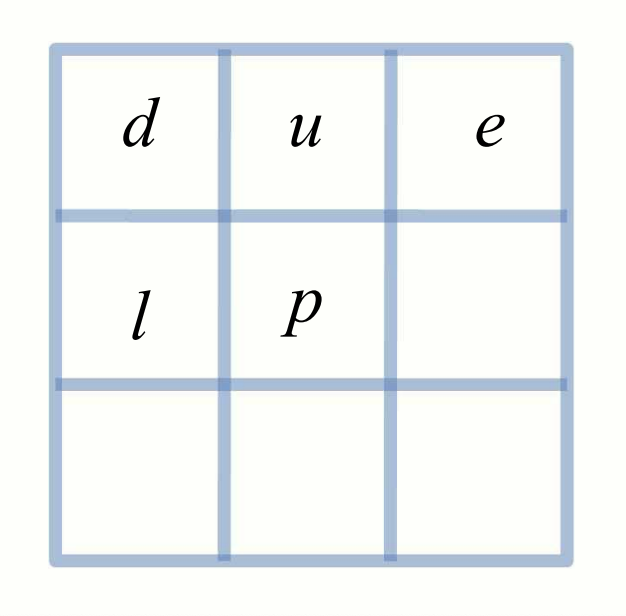
예시

다음과 같은 픽셀들을 component labeling 해보겠습니다.

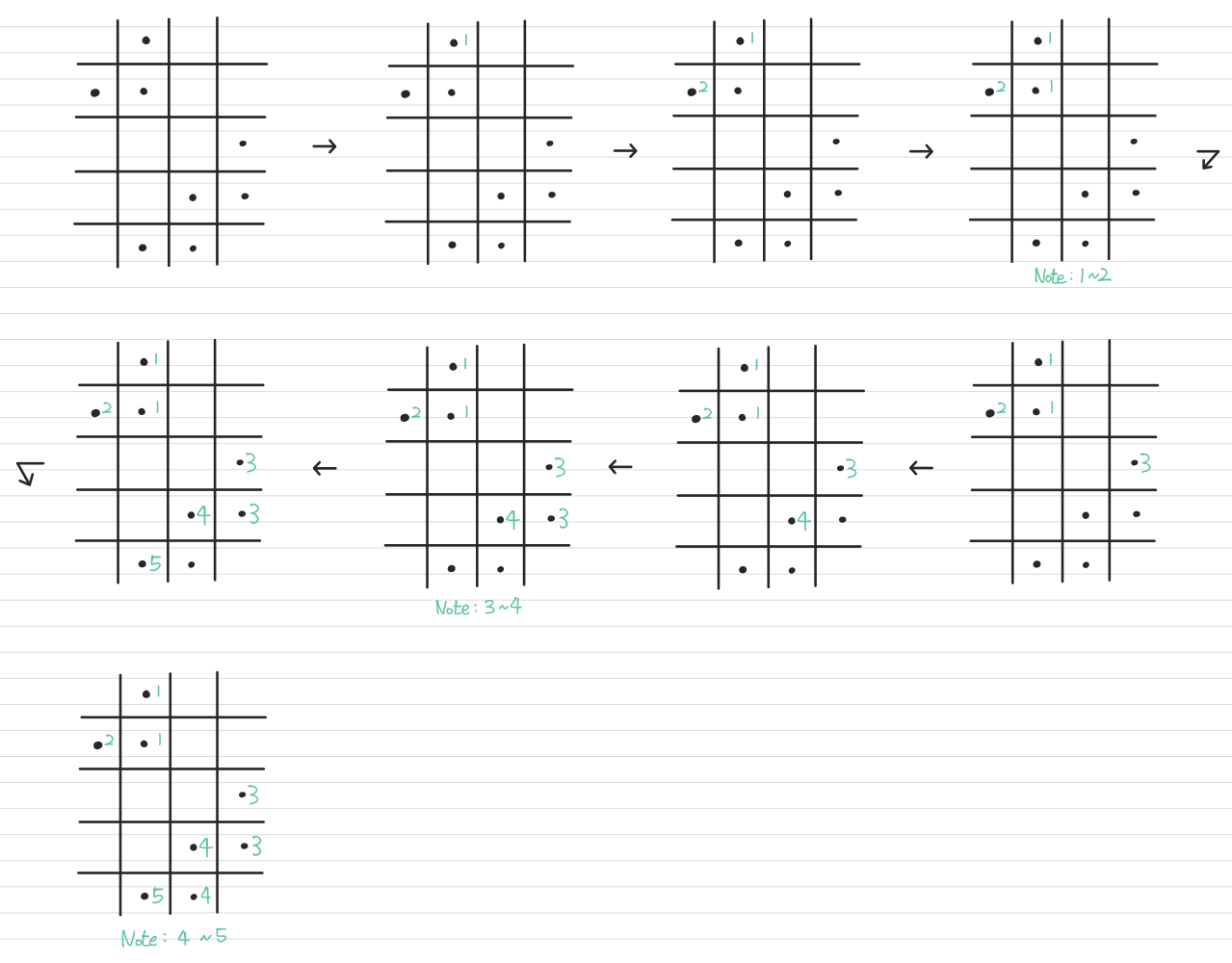
Component Labeling 과정 예시

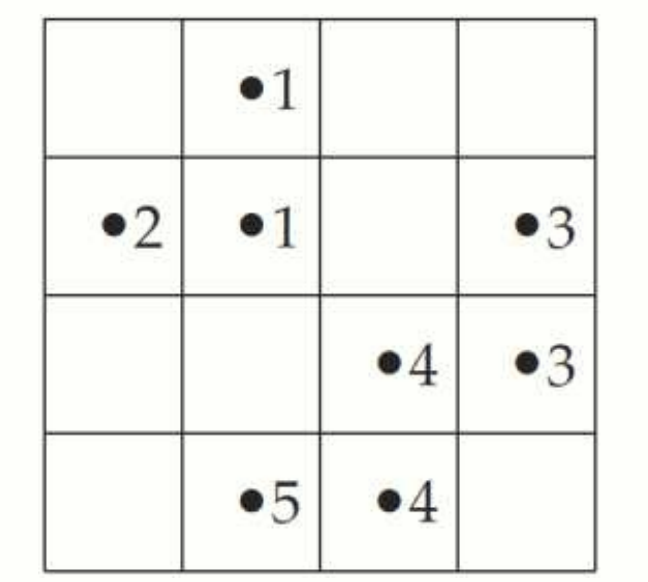
Component Labeling 결과

구현

skimage.measure.label(image, connectivity=1, background=0)

• image: 입력 binary image
• connectivity:
  • 1: 4-connected
  • 2: 8-connected
  • background: 배경값을 지정. 기본값은 0.

Binary numpy array 의 4-component 와 8-component 를 각각 구해보자.

import numpy as np
import skimage.measure as sm

image_example = np.array([[0, 0, 0, 0, 0, 0, 0],
						  [0, 0, 1, 1, 1, 0, 0],
                          [0, 0, 1, 1, 1, 0, 0],
                          [0, 0, 1, 1, 1, 0, 0],
                          [0, 1, 0, 0, 0, 0, 0],
                          [0, 1, 0, 1, 1, 1, 1],
                          [0, 0, 0, 1, 1, 0, 0]])
C4 = sm.label(image_example, connectivity=1)  # 4-component
C8 = sm.label(image_example, connectivity=2)  # 8-component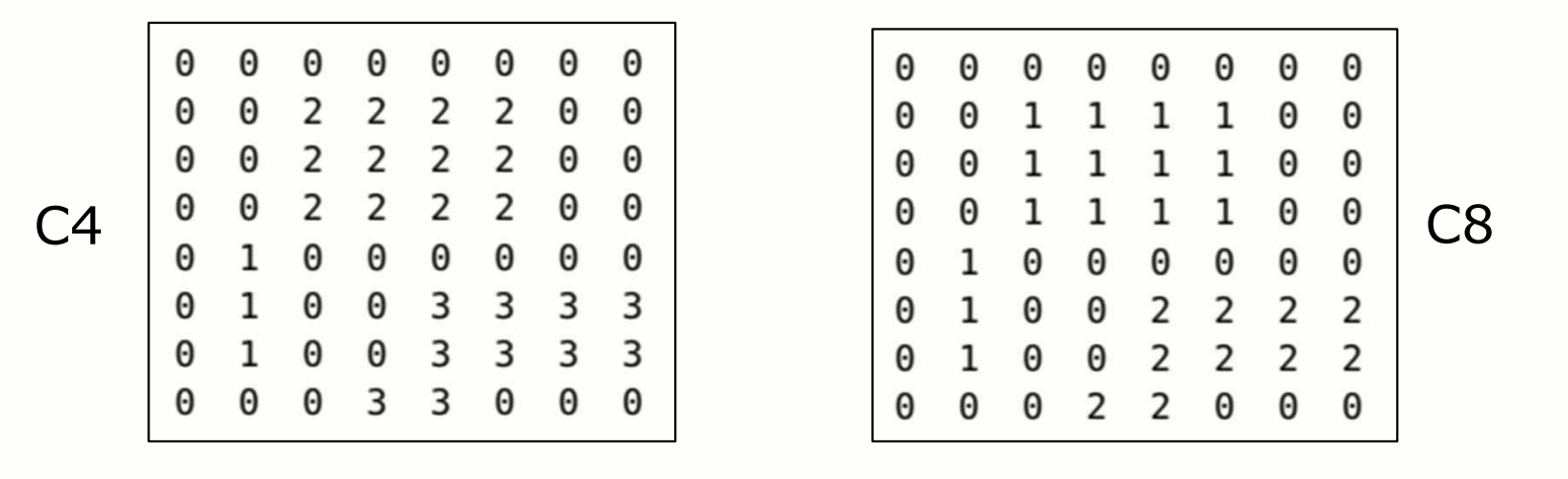

이번엔 임의의 binary image 에서 덩어리진 Foreground 요소가 총 몇 개인지 구해보자.

import numpy as np
import skimage.measure as sm
import skimage.morphology as mo
import matplotlib.pyplot as plt

N = plt.imread('pinenuts.png')
N1 = N < 124  # 픽셀 값이 124보다 작은 영역을 Foreground 로 설정
c4 = np.array([[0, 1, 0],
			   [1, 1, 1],
               [0, 1, 0]])  # 십자 모양 SE
N2 = mo.binary_opening(N1, footprint=c4)
C4 = sm.label(N2, connectivity=1)  # 4-connected

print(C4.max())  # 73; 73개의 connective components 가 존재한다는 의미

Distance Transform

---

Distance transform 은 이미지에서 특정 픽셀(예: Foreground)로부터 다른 픽셀들까지의 최소 거리를 계산하여, 각 픽셀에 거리 값을 할당하는 기법입니다.

Distances and Metrics

거리 함수와 조건

거리 함수 $d(x, y)$ 는 두 점 $x$ 와 $y$ 사이의 거리를 계산하는 함수로, 다음 조건을 만족해야 metric(거리 함수) 라 부릅니다:

1. 대칭성(Symmentry): $d(x, y) = d(y, x)$

2. 양의 값(Positivity): $d(x, y) \geq 0$ 이고, $d(x, y) = 0 \iff x = y$

3. 삼각 부등식(Triangle Inequality): $d(x, y) + d(y, z) \geq d(x, z)$

주요 거리 측정법

(1) 유클리드 거리(Euclidean Distance):

• 두 점 $x = (x_1, x_2) , y = (y_1, y_2)$ 사이의 거리:

(2) $d_4$ 거리:

• Taxicab Distance 라고도 불리며, 격자에서 직각 경로를 통해 계산됩니다.

• 만약 $x = (0, 0), y = (2, 5)$ 라면 $d_4(x, y) = 7$ 입니다.

(3) $d_8$ 거리:

• 격자 대각선까지 포함하는 거리입니다.

• 만약 $x = (0, 0), y = (2, 5)$ 라면 $d_8(x, y) = 5$ 입니다.

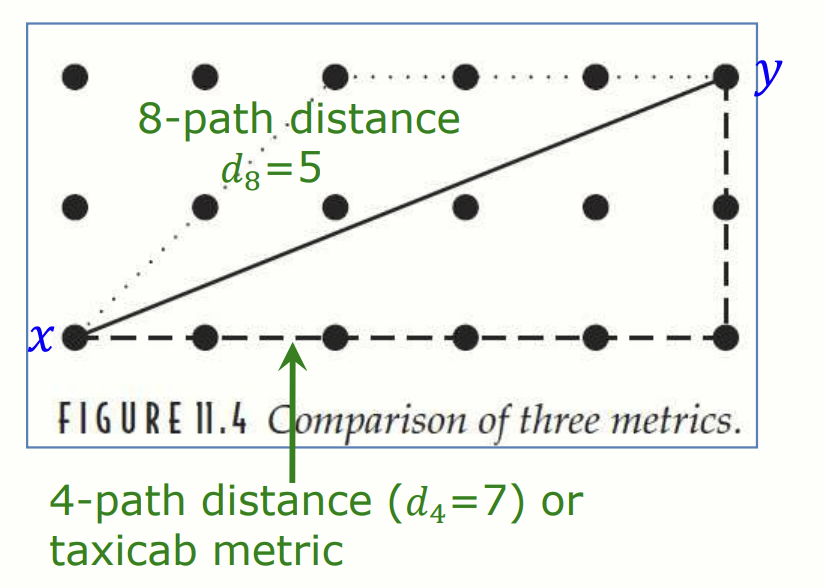
d4 거리와 d8 거리 비교.

Distance Transform

Distance Transform 은 이미지 내 특정 영역(예: Foreground, $R$)으로부터 모든 픽셀의 거리를 계산하는 방법입니다.

방법 1: 직접 계산

모든 $(x_1, y_1)$ 픽셀에 대해 $R$ 내의 모든 픽셀과의 유클리드 거리를 계산하고, 최소값을 선택합니다:

이 방법은 계산 비용이 높다는 단점이 있습니다.

방법 2: Distance Transform 알고리즘

효율적으로 계산하기 위해서는 distance transform 을 사용하는 것이 좋습니다.

Step 1) 초기화: $R$ 에 속한 픽셀은 0, 나머지는 $\infty$ 로 초기화합니다.

Step 2) 갱신: 주변 이웃 픽셀과의 최소 거리 값을 반복적으로 계산합니다. 이 때 distance mask을 씌워 이웃값들을 구합니다:
$m_d(x_1, x_2) = \min(\text{현재 값}, \text{이웃 값} + 1)$

Step 3) 모든 픽셀 값이 갱신될 때까지 Step 2를 반복합니다.

예시

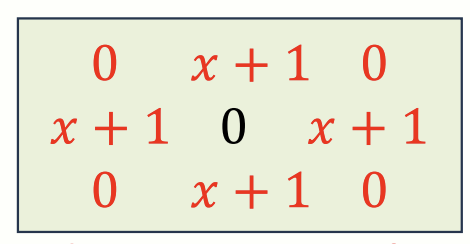
Distanc mask. 반드시 이와 같을 필요는 없다.

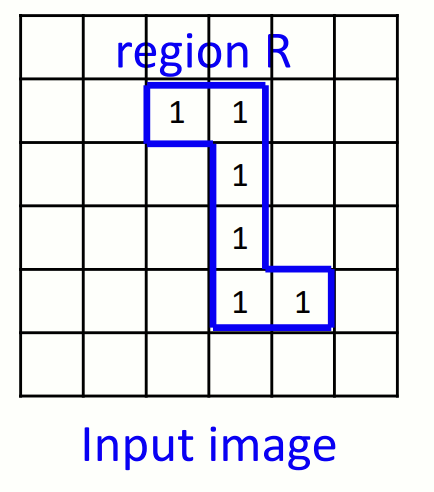
Input image.

위와 같은 distance mask 와 input image 가 있다고 가정합시다. 이 mask를 이용하여 input image 를 distance transform 시키는 과정은 아래와 같습니다.

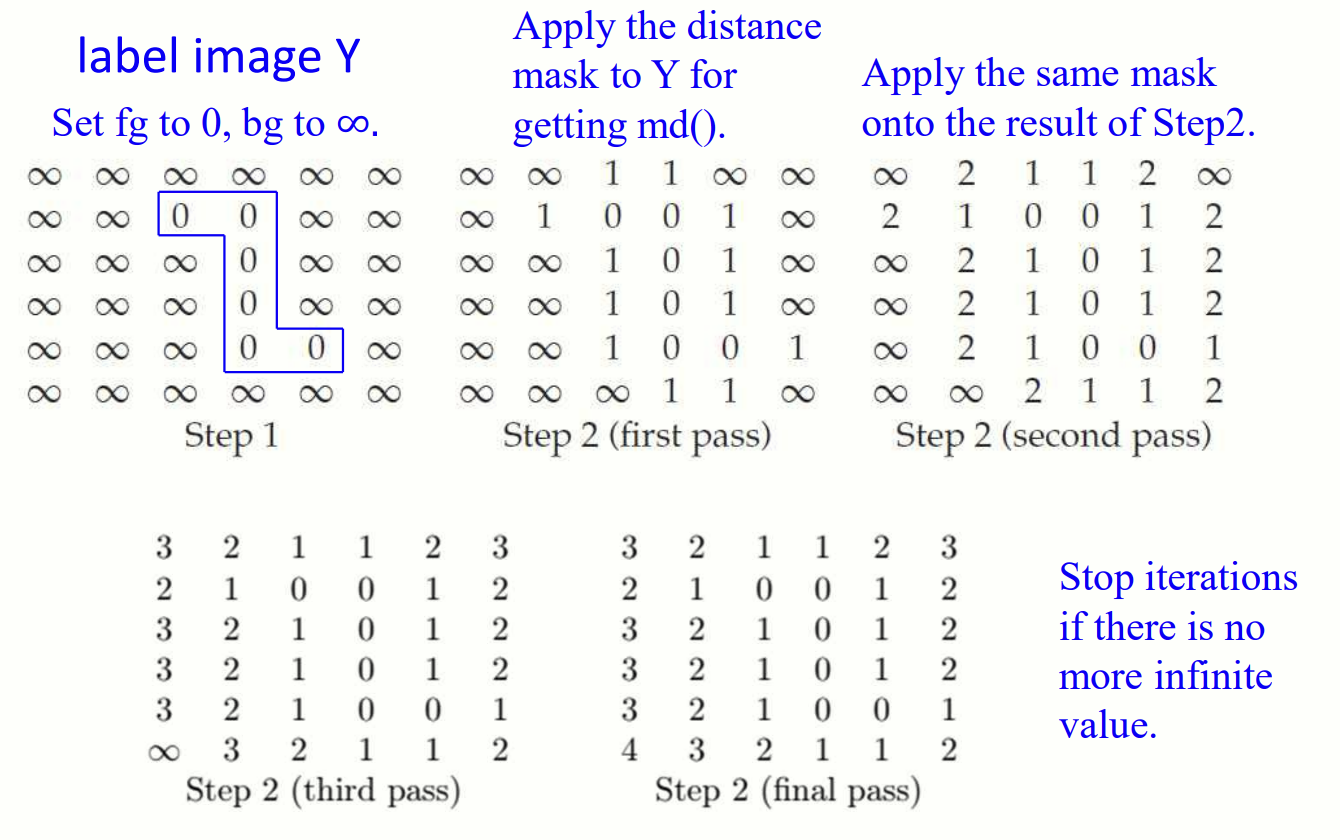
상황에 따라 distance mask 를 바꿀 때도 있습니다.

Distance mask 만 변경한 case.

Two-Pass Distance Transform

거리 계산을 효율적으로 수행하기 위해 두 번의 스캔(pass)으로 거리 값을 업데이트하는 distance transform입니다.

첫번째 스캔에서는 좌측 산단(top-left)에서 우측 하단(bottom-right)으로 초기 거리 값을 계산합니다.

두번째 스캔에서는 우측 하단(bottom-right)에서 좌측 상단(top-left)으로 역방향으로 진행하며 값을 수정합니다.

이 방법은 일반적인 distance transform 과 결과는 정확히 일치하면서 속도는 더욱 빠릅니다.

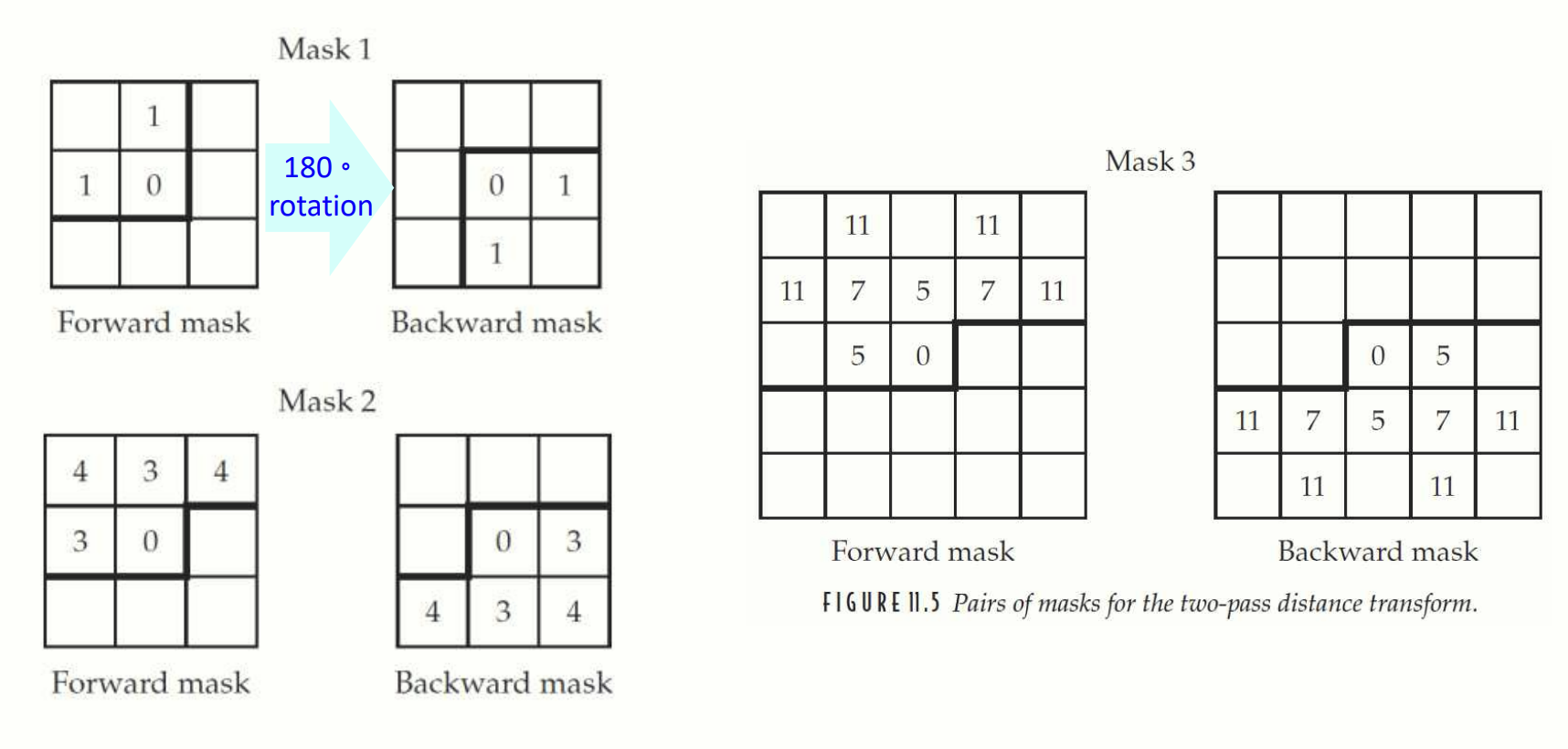
Distance mask 예시.

구현

Distance transform 을 구현하기 위해서는 다음과 같은 사항들을 고려해야합니다:

1. 이미지 패딩(Padding):

• 마스크의 크기에 따라 이미지를 적절해 패딩합니다.

• 경계 처리 때문에 0 값으로 패딩을 추가합니다.

2. 초기화:

• Foreground(객체)는 0으로 설정

• Background(배경)는 $\infty$로 설정

3. Forward 와 Backward Mask 생성:

• Forward Mask: 거리 값을 계산하는 첫 번째 방향(좌측 상단 -> 우측 하단)

• Backward Mask: Forward Mask 를 180도 회전한 형태로, 두 번째 방향(우측 하단 -> 좌측 상단)

4. Forward Pass:

• 각 픽셀에서 이웃 픽셀과 Forward Mask 를 사용해 최소 거리 값을 계산

• 왼쪽에서 오른쪽, 위에서 아래로 진행

5. Backward Pass:

• Forward Pass 로 업데이트된 결과를 사용

• Backward Mask 를 사용하여 다시 최소 거리 값을 계산

• 오른쪽에서 왼쪽, 아래에서 위로 진행

def disttrans(image, fmask):
	# Backward Mask 생성: Forward Mask 를 180도 회전
    backmask = np.rot90(fmask, 2)
    mr, mc = fmask.shape
    if mr % 2 == 0 or mc % 2 == 0:
    	raise ValueError("Error: Mask must have odd numbers of rows and columns")
    r, c = image.shape
    nr = (mr - 1) // 2
    nc = (mc - 1) // 2
    
    # 패딩 추가 및 초기화: np.pad 를 사용해 이미지에 패딩을 추가하고, 0 값을 무한대로, 1 값을 0으로 설정합니다.
    image2 = np.float64(np.pad(image, ((nr, nr), (nc, nc)), mode='edge'))
    image2[np.where(image2 == 0)] = float('inf')
    image2[np.where(image2 == 1)] = 0
    
    # Forward Pass: 현재 픽셀과 이웃 픽셀 값을 비교해 최소값을 계산합니다.
    for i in range(r):
    	for j in range(c):
	        image2[i+nr, j+nc] = (image2[i:i+mr, j:j+mc] + fmask).min()
    
	# Backward Pass: 이전 pass 에서 계산된 값을 기반으로 다시 최소값을 계산합니다.
	for i in range(r)[::-1]:
	    for j in range(c)[::-1]:
    	    image2[i+nr, j+nc] = (image2[i:i+mr, j:j+mc] + backmask).min()
            
	return image2[nr:nr + r, nc:nc + c]

결과 예시.