Lazy Propagation In Segment Tree

일부 updates를 미루면서, 구간 updates를 최적화 시키는 알고리즘

Problem

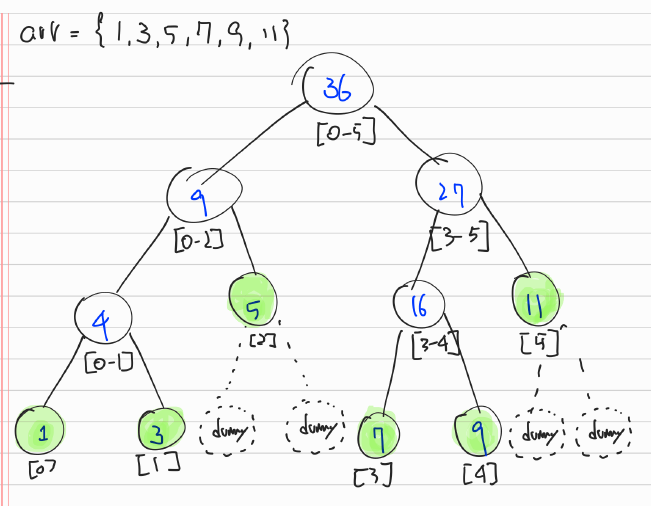
위의 그림은, 구간의 합을 저장하는 Segment Tree이다. 이를 통해, 하나의 값을 갱신할 때, 구간의 합도 O(logN)이라는 빠른 시간 안에 update 할 수 있다.

그러나, 값 하나를 update 하는 게 아니라, 특정 range의 모든 값들을 update해야 한다면 어떨까? range가 M이라고 할 때 O(MlogN)이 걸린다.

물론, 기본 Segment Tree도 빠르지만, 이런 상황이 계속 주어지면 많은 시간을 요구하게 된다.

Solution

Lazy Propagation
최상단의 대상 node만 update를 적용하고, 자손들은 나중에 update한다(lazy).
이후 query나 update 등을 수행하다 lazy가 붙은 node에 접근할 일이 생기면, 그때 update 해준다. 그 자손들은 역시 lazy하게 남긴다.

예를 들어, 위와 같은 상황에서 arr[3]부터 arr[5]까지의 값들에 10을 더한다고 가정해 보자. ST에서 27이 저장된 node에 10*3 을 더해주고, 나머지 children nodes는 필요시 다음에 update 한다.

아래는 pseudocode이다.

/* val[l...r]을 updates 해야할 때,
 * ST를 update하는 함수
 * */
updateRange( l, r ):
  1) 현재 node에 pending updates가 있다면,
      a) update를 진행한다.
  2) 현재 node가 update 대상 구간이라면, 
      a) update: 현재 node를 update한다.
      b) postpone: 차후에 진행할 lazy 값을 저장하여, children nodes의 update를 미룬다.
  3) 현재 node가 update 대상 구간을 일부 포함,
      a) recursive call을 통해 좌우 구간을 update

시간 복잡도는 O(logN)이다.

Data Structure

• ST[size], Segment Tree 저장용
• lazy[size], pending updates 저장용. ST[idx]에 대한 값을 lazy[idx]에 저장.

(size나 다른 자세한 내용은, Segment Tree 링크를 참조.)

EXAMPLES

• EX1)