Segment Tree
구간 사이의 정보를 저장하는 Data Structure
Problem
아래의 문제를 생각해 보자.
size가 n인 array가 있을 때, 두 가지 operation을 생각할 수 있다.
1. Range Sum query: l부터 r까지 값들의 합 ( 0 <= l <= r <= n - 1 )
2. Update: array[i]의 값을 변경하기
Solutions
다음과 같은 세 가지 해결 방법을 떠올릴 수 있다.
1) Brute Force
2) Sum Array
3) Segment Tree
1) Brute Force
- Query: Naive하게 l 부터 r까지 더한다. 시간 복잡도는 O(n)이다.
- Update: array[i] 값 하나를 바꾼다. 시간 복잡도는 O(1)이다.
update는 얼마든지 들어와도 빠르게 처리하지만, query가 많다면 적합하지 않은 방법이다.
2) Sum Array (prefix sum)
0~i 까지의 합을 미리 계산하여, sumArray[i]에 저장한다.
- Query: sumArray를 활용하면 구할 수 있다. O(1)이 걸린다.
- Update: array[i] 값을 변경할 때, sumArray[i...n]을 수정해야 한다. O(n)
query에는 가장 빠르다. 다만 update 필요 시 비효율적이다.
3) Segment Tree
반면에 Segment Tree는 O(1)보다는 느리지만, 모든 상황에서 시간 복잡도가 O( logn )이다.
ST의 특성은 다음과 같다.
- 색칠된 leaf nodes가 array의 elements이다.
- 나머지는 자식 노드의 합을 저장한다.
- [ ]는 구간을 나타낸다.
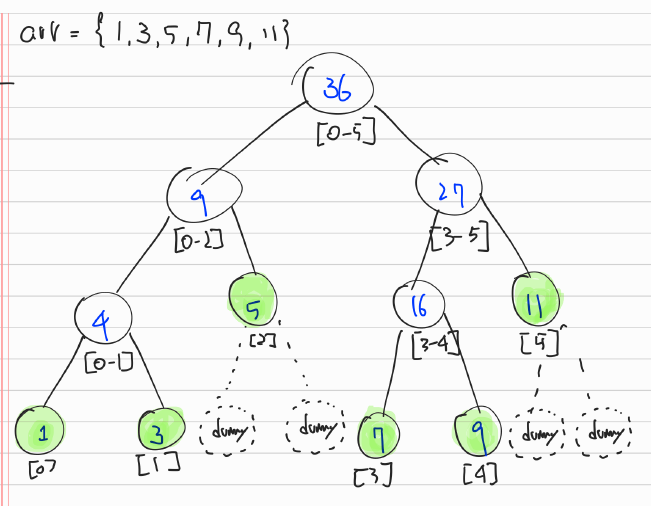
필요 nodes 개수
elements가 n개, 그 사이에 n-1개가 있으므로, 총 2n-1개 이다.
(이는 dummy를 제외한 크기이다. )
ST의 크기
그림을 보며 계산해보면,
height = ceil( log2(n) ) 이다.
따라서, size = 2^(height+1) - 1 인 array를 사용하여 ST를 생성해야 한다.
(이는 dummy를 포함한 크기이다.)
(size 계산 시, double 형인 pow를 쓰기보다는, ( 1 << (h + 1) ) - 1 와 같이 직접 계산하는 게 좋다. 이때, 괄호로 정확히 연산 순서를 명확히 해줄 필요가 있다.)
정리
위의 특성을 기반으로, 아래와 같이 구현할 수 있다.
- Construction: recursive call을 통해 구현, O( n )
- Query: recursive call을 통해 검색, O( logn )
- Update: recursive call로 update, O( logn )
TIP
ST vs Prefix Sum
단순히 range query만 보면 O(logN) vs O(1)이다.
update가 없다면 Prefix Sum이 훨씬 빠르다.
prefix sum 계산
range(left, right)에 대해 val을 갖는 data가 존재할 수 있다. 이에 대한 prefix sum이 필요한 경우, 아래와 같이 연산을 최적화할 수 있다.
preSum[l] += val;
preSum[r] -= val;Segment Tree 축
직접적인 range가 아닌 index를 기반으로 축으로서 사용할 수도 있다.
ex1
EXAMPLES
Segment Tree를 적용하는 대표적인 문제들은 다음과 같다.
1. Sum of given range
2. Range minimum query
3. Product of given range
..
심화
- Lazy Propagation in Segment Tree
- Persistent Segment Tree
- Fenwick Tree