본 글은 2009년에 발표된 Matrix Factorization Techniques for recommender systems를 읽고 요약 및 정리한 글입니다.
1. 추천 시스템
1-1. 추천 시스템의 필요성
- 온라인 시장이 되면서 유저들이 상품(ex. movies, music, TV shows and etc)을 선택할 수 있는 폭이 굉장히 넓어짐
- 적절한 상품을 고객에게 연결해주는 것이 서비스에 대한 만족감과 충성도를 강화하는 핵심
1-2. 대표적인 추천 방법
- CB(Content Filtering)
정의: 고객과 상품에 대한 프로필을 작성하여 그 특성으로 추천
장점: 유저의 과거 행적 데이터가 없어도 추천 가능(cold-start problem에 강함)
단점: 외부 정보는 모으기 쉽지 않음고객(users): 성별, 나이 등의 정보와 적절한 질문지에 대한 대답
영화(products): 장르, 배우, 박스오피스 인기도 - CF(Collaborative Filtering)
정의: 고객과 상품의 상호 의존성을 분석하여 새로운 관계를 추천
장점: 도메인에 무관하게 사용가능하고 보통 더 좋은 정확도(Domain Free, Accurate)
단점: 새 고객과 상품에 대한 추천이 불가능집단지성!
나와 비슷한 사용자는 어떤 상품에 관심을 가졌는가
시스템 내에서 유저가 상품에 대한 history 데이터를 이용
1-3. CF의 방법론
-
Neighborhood methods
- 상품 혹은 고객의 관계(Relationship)에 집중한 방법
- Item-oriented
한 유저의 특정 상품에 대한 평가는 이웃 상품을 이용 - User-oriented
한 고객의 특정 상품에 대한 평가는 이웃 고객을 이용
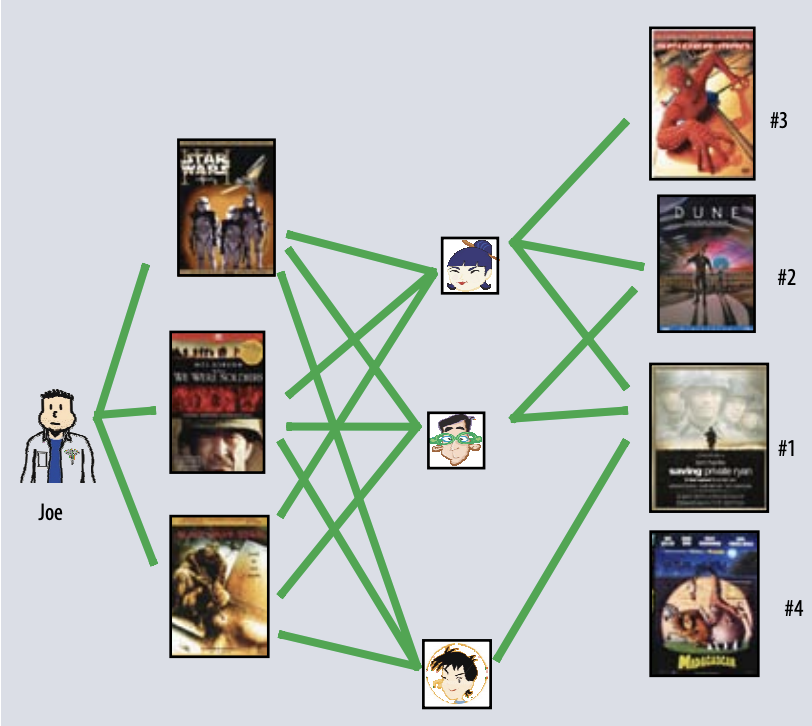
User-Oriented neighborhood method
a. Joe는 3가지 영화를 좋아한다
b. 이 영화들을 좋아하는 사람들을 찾는다
c. 그들이 좋아하는 다른 영화를 찾는다
d. 3명다 좋아하는 Private Ryan 먼저 추천
e. 2명이 좋아하는 Dune 을 다음에 추천
-
Latent Factor model
- 상품 혹은 고객의 점수(Rating)를 설명하는데 집중한 방법
- Latent Factor는 인간이 만든 특징에 대한 컴퓨터화된 대안
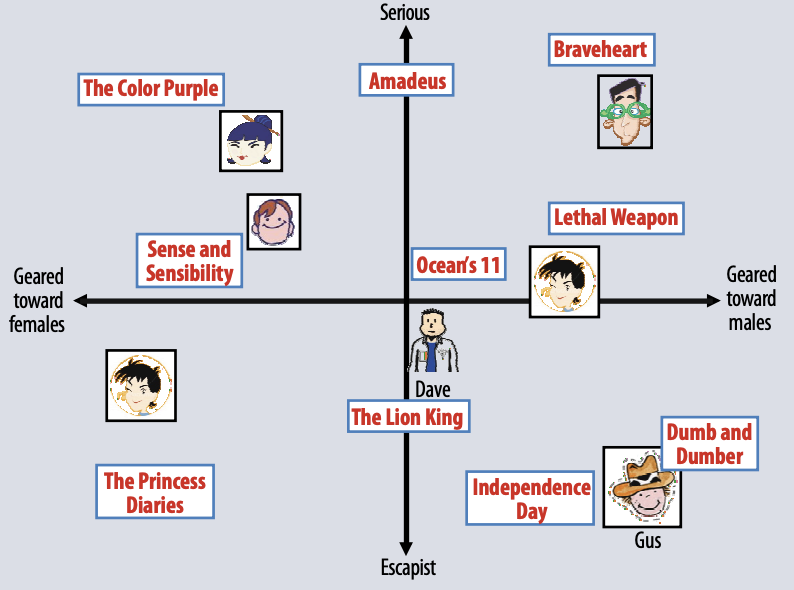
Latent Factor Approach
2개의 차원을 이용해서 고객과 영화에 대해 특징을 짓는다
a. male vs female
b. serious vs escapist
2. 추천 시스템의 전략
2-1. MF(Matrix Factorization)
- 상품 평점 패턴을 추론하는 고객과 상품의 factor vector를 이용
- 상품과 고객의 factor가 서로 상응할 수록 추천으로 이어짐
- scalabilty, accuracy, flexibility
2-2. Feedback Data
- Explicit Feedback
- 상품에 대한 직접적 관심도
- 유저들은 가능한 상품에 대해 아주 적은 행동 데이터
- ex. star rating(Netflix), thumbs-up or thumbs-down(TiVo)
- Implicit Feedback
- 상품에 대한 간접적 선호도
- 고객들의 행동 데이터를 관찰하여 좀 더 많은 데이터
- ex. purchase history, browsing history, search patterns, mouse movements
2-3. MF 수식
- Matrix Factorization Model
Map: 고객과 상품을 동일한 차원의 Latent Space
Model: user-item interaction를 inner product는 item에 대한 latent factor, 는 user에 대한 latent factor
추천 시스템은 이 수식을 이용해 유저가 어떤 아이템에 어떤 점수를 줄지 예상할 수 있다 - 학습전략
- 위의 수식 (1)은 SVD와 매우 관련
- 전통적인 SVD는 missing value가 많은 matrix를 해결할 수 없음
- observed rating만 이용하되 regularized squared error를 이용하여 overfitting을 피함(Generalization)
where
-
SGD(Stochastoc Gradient Descent)
-
ALS(Alternating least squares)
- 위의 수식에서 와 는 미지수이기 때문에 수렴하지 않을 수 있다
- 하지만 하나를 고정하면 quadratic하게 해결 가능
- 돌아가며 하나의 변수를 고정하여 업데이트
-
Adding Biases
- 사람마다 평가에 대해 평균적 성향(경향성)이 존재
- user bias( ): 어떤 사용자는 전체적으로 점수를 높게/낮게 주는 경향이 있음
- item bias( ): 어떤 아이템은 전체적으로 점수가 높게/낮게 매겨지는 경향이 있음
- global mean( ): 특정 데이터셋의 평균 평점
where
3. 추가적인 입력 데이터
실제 추천 시스템에서는 cold start problem을 해결해야 한다
따라서 rating matrix만으로는 정보가 부족하다
이를 보완하기 위한 다양한 추가 정보:
- Implicit feedback: 클릭, 시청, 장바구니 담기, 구매 기록
- Temporal dynamics: 시간에 따른 취향 변화, 아이템 인기 변화
- Content/context: 아이템 장르, 설명, 가격, 사용자 프로필, 접속 상황
- Social information: 친구/팔로우 관계
