CodeUp_1505,1506_달팽이배열_및_역달팽이배열_풀이

CodeUp 문제집 중 2차원배열 내가 시도 했던 방법과 reference를 참고하여 더 간단한 방법으로 코드를 작성한 것에 대한 글이다.

문제는 다음과 같다

첫 시도 방법 : 다른 장치 없이 이중 for문과 조건문 만을 이용하여 구현

노트에 적어가며 규칙을 찾아보고자 했지만 몇 시간 동안 고민해봐도 결국 찾을 수 없어 구글 검색을 하였다.

reference 관련 게시글

해당 블로그에 게시글을 보고 힌트를 얻었다.

바로 이동할 방향을 전환할 리스트와 방향 전환 리스트에 접근할 인덱스 변수를 이용하는 것이다.

# 상, 우, 하, 좌
dr = [-1,0,1,0]
dc = [0,1,0,-1]

# nr: next row, nc: next column
# cr: current row, cc: current column
r = 0 # 현재 위치의 y좌표
c = 0 # 현재 위치의 x좌표


d = 2 # 방향 전환 리스트 원소 값에 접근할 인덱스 값코드를 입력하세요

이 장치를 보자마자 바로 Dynamic Programming (동적계획법)을 이용해서 풀면 되겠다고 생각하였다

따라서 다음과 같은 순서로 풀게 되었다.

1. 2차원 리스트 (DP테이블) 생성 (모든 원소 0으로 초기화)

2. 방향전환을 위한 2개의 리스트 생성 (x좌표에 대한 리스트, y좌표에 대한 리스트)

3. 방향전환을 위해 방향전환리스트를 이용하기 위한 인덱스 접근용 변수 'd' 선언

4. 총 1부터 n*n까지 1씩 증가한 값들이 필요하므로 'count' 라는 변수 선언하여 1로 초기화

5. while문을 사용하고 count가 n*n을 초과할 때까지 반복

6. 방향전환이 필요한 경우(인덱스 범위 초과, 이미 값이 입력된 위치)와 방향전환이 필요 없는 경우로 조건문 구성

7. DP테이블의 모든 인덱스에 대해 원소 채워넣기

8. 완성된 DP테이블을 이중 for문 이용하여 순서대로 n by n 형태의 배열로 출력

위와 같은 순서로 코드를 구현했을 때 다음과 같다.

## 도무지 모르겠어서 reference 참고
# 인덱스를 활용해서 방향전환을 하고 싶을 대 'delta row'와 'delta column'리스트를 만들고
# 접근하면 됨!

# 상, 우, 하, 좌
dr = [-1,0,1,0]
dc = [0,1,0,-1]

# nr: next row, nc: next column
# cr: current row, cc: current column
cr = 0 # 현재 위치의 y좌표
cc = 0 # 현재 위치의 x좌표
nr = 0 # 다음 위치의 y좌표
nc = 0 # 다음 위치의 x좌표

d = 1 # 방향 전환 리스트 원소 값에 접근할 인덱스 값

n = int(input()) # 사용자로부터 2차원 배열의 크기 입력 받음
dp_list = [[0]*n for _ in range(n)] # 이차원 배열의 원소값들을 저장할 dp 리스트 생성

count = 1 # 원소의 저장할 값
while 1:
 if count == (n*n + 1): # n*n 배열이므로 n*n 번째 숫자가 채워지면 break
   break
 else:
   dp_list[cr][cc] = count # 현재 위치에 count 값 저장

   # 다음 위치 계산
   ## 처음 위치를 제외한 꼭지점 위치일 때 방향 전환해야 됨
   if ((cr == 0 and cc == n-1) or (cr == n-1 and cc == n-1) or (cc == 0 and cr == n-1)):
     d = (d + 1) % 4 # (우 -> 하 -> 좌 -> 상 1->2->3->0)시계방향으로 순환하도록 4로 나눠줌
     nr = cr + dr[d] 
     nc = cc + dc[d]
     count += 1
     cr = nr
     cc = nc
   ## 꼭지점 위치의 값은 아닌 경우
   else:
     ### 그 다음 위치가 0이 아닌경우 (이미 지나친 경우) -> 방향전환해야됨
     tr = cr + dr[d] # 원래 진행방향으로 진행할 경우 다음 위치의 y좌표 (그대로 진행할 경우 그 위치가 이미지나친 경우인지를 판별하기 위해)
     tc = cc + dc[d] # 원래 진행방향으로 진행할 경우 다음 위치의 x좌표 (그대로 진행할 경우 그 위치가 이미지나친 경우인지를 판별하기 위해)
     if dp_list[tr][tc] != 0 :
     	d = (d + 1) % 4 # (우 -> 하 -> 좌 -> 상 1->2->3->0)시계방향으로 순환하도록 4로 나눠줌			
       nr = cr + dr[d] 
       nc = cc + dc[d]
       count += 1
       cr = nr
       cc = nc

     ### 방향을 전환해야되는 경우가 아닌 경우들
     else : # 이전에 갔던 방향과 동일한 방향으로 그대로 이동
       nr = cr + dr[d] 
       nc = cc + dc[d]
       count += 1
       cr = nr
       cc = nc

# 완성된 dp 테이블로부터 달팽이 2차원 배열 출력:
for i in range(n):
 for j in range(n):
   print(dp_list[i][j], end = ' ')
 print()


# 이것보다 훨씬 간단하게 짤 수 있다!!!!!!!!!!!!
# 코드가 길어진 이유가 다음 이동 위치가 0인지 아닌지를 판별하기 위해
# 다음 위치가 인덱스가 범위를 초과하는 인덱스인지와 따로 구별하였는데
# 그렇게 하지 않고 하나의 조건문에서 다 판별할 수 있고
# 그렇게 하기 위해서는 일단 다음 인덱스가 0이 아닌경우를 다시 빼주면 됨 (실행 취소)
# nr nc cr cc tr tc 가 아닌 그냥 c r 2가지 만으로도 짧게 구현 가능

참고했던 방향전환 방법이 나와있는 게시글의 풀이방법과 비교해보았고 필자가 짠 코드는 비교적 훨씬 길고 참고 게시글의 풀이방법이 더 효율적이고 간단하여 다음 역달팽이배열 문제에서 더 간략하게 다시 코드를 작성해봤다.

변경한 것들

1.	DP테이블 인덱스 접근하기 위한 변수 종류 변경
	tr, tc, nr, nc, cr, cc -> r, c
	tx : 다음 이동할 인덱스가 유효한 위치인지 판단하기 위한 임시 인덱스
    nx : 다음으로 이동할 인덱스의 위치
    cx : 현재 위치의 인덱스
    
    기존 방식은 이렇게 3가지 경우로 나누어 변수를 선언
    
    -> r,c 만을 단 두 개의 변수만을 이용

2. 다음 위치 계산 및 이동 방법 변경
	이전 방법 :현재 위치에 값을 넣고 경우에 따라 다음 위치 결정
	변경한 방법: 
    	-> 현재 위치에 값 넣기 
        -> 바로 이전에 움직였던 방향으로 위치 이동 한 후
        -> 이동한 위치가 유효한 위치인지 판별
        -> 유효한 위치면 다음 차례 실행, 유효X 라면 실행취소 (인덱스 값 변경 이전 값으로 다시 변경)

3. 방향전환 인덱스 값 변경 방법
	d == 0 : 상
    d == 1 : 우
    d == 2 : 하
    d == 3 : 좌
    시계 방향으로 방향을 전환하므로 해당 인덱스 값이 순환해야 됨
이전 방법 : 조건문 사용
변경한 방법 : % 연산 이용 (d = (d + 1) % 4)
	-> 역달팽이 배열문제에서는 사용하지 않음
    -> 위 첨부한 코드는 변경 전 코드지만 이 부분만 변경한 방법으로 업데이트 해서 올림
    
    

# 역달팽이

# 상, 우, 하, 좌
dr = [-1,0,1,0]
dc = [0,1,0,-1]

# nr: next row, nc: next column
# cr: current row, cc: current column
r = 0 # 현재 위치의 y좌표
c = 0 # 현재 위치의 x좌표


d = 2 # 방향 전환 리스트 원소 값에 접근할 인덱스 값

n = int(input()) # 사용자로부터 2차원 배열의 크기 입력 받음
dp_list = [[0]*n for _ in range(n)] # 이차원 배열의 원소값들을 저장할 dp 리스트 생성

count = 1 # 원소의 저장할 값
while 1: 
  if count == (n*n + 1): # n*n 배열이므로 n*n 번째 숫자가 채워지면 break
    break
  else:
    dp_list[r][c] = count # 현재 위치에 count 값 저장
    r += dr[d] # 다음 위치 업데이트
    c += dc[d] # 다음 위치 업데이트
    count += 1 # 다음 원소값 업데이트

    # 방향 전환이 필요한 경우 실행 취소
    if r < 0 or r >= n  or c < 0 or c >= n or (dp_list[r][c] != 0):
      r -= dr[d] # y좌표 아동 실행 취소
      c -= dc[d] # x좌표 아동 실행 취소
      
      #방향 전환 (시계방향 (1,2,3,0 -> 우,하,좌,상))
      if d == 0:
        d = 3 # 상 -> 좌 (다시 인덱스 3으로 순환되어야 하므로)
      else:
        d -= 1
      #방향 전환 후 다음 위치 다시 업데이트
      r += dr[d] # 다음 위치 업데이트
      c += dc[d] # 다음 위치 업데이트

# 완성된 dp 테이블로부터 달팽이 2차원 배열 출력:
for i in range(n):
  for j in range(n):
    print(dp_list[i][j], end = ' ')
  print()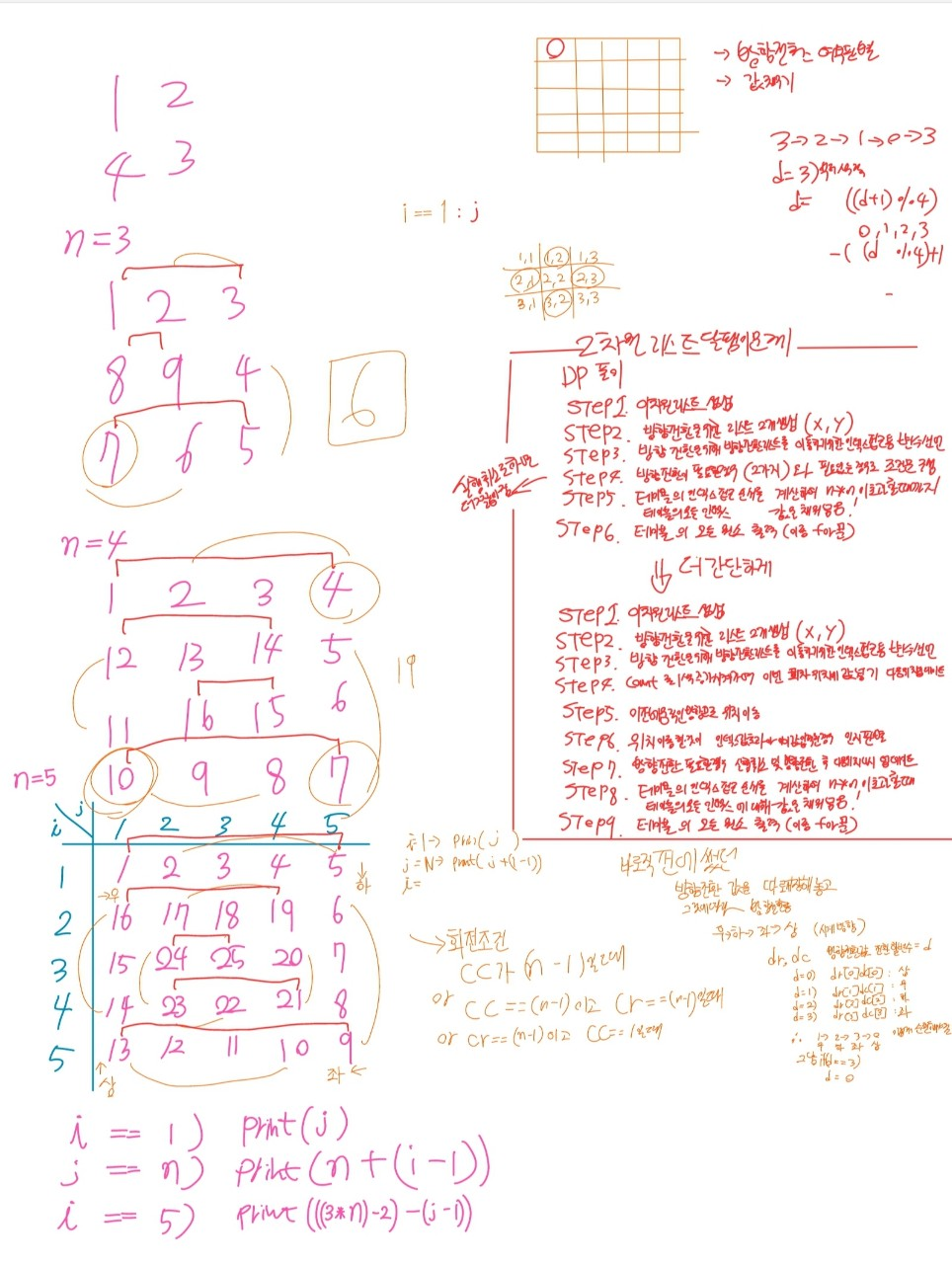

해당 문제는 풀기 위한 방법을 고민하는데 너무 많은 시간을 할애하였고, 시간이 무한정하지 않으므로 알고리즘을 풀 때 고민할 수있는 시간을 fix 시켜 놓고 해당 시간이 초과하면 바로 reference를 찾아보는 것이 좋은 방법일지에 대해 생각해보는 계기가 되었다.