[프로그래머스] 타켓넘버 Python

미로찾기, connected component 개수 찾기와 같이 상하좌우, map 문제 뿐만 아니라, 이진트리형식으로 만들 수 있는 문제 또한 DFS&BFS 방식으로 접근할 수 있음을 알게되었다.

DFS&BFS를 연습하려고 풀려했으나 도무지 모르겠어서 아래의 게시물을 참고하여 풀었다.

Reference

실전이라고 생각하고 DFS나 BFS로 풀 수 없다면, itertools의 product 이용해서 repeat를 len(numbers)로 설정하고 모든 경우의 수를 확인하는 완전탐색으로 풀고자 했다. 예상했듯이 테스트 케이스 2개가 시간초과로 실패하였다.

아래의 그림을 통해 예시 case에 대해 그래프로 모든 경우의 수를 나타내보았다.

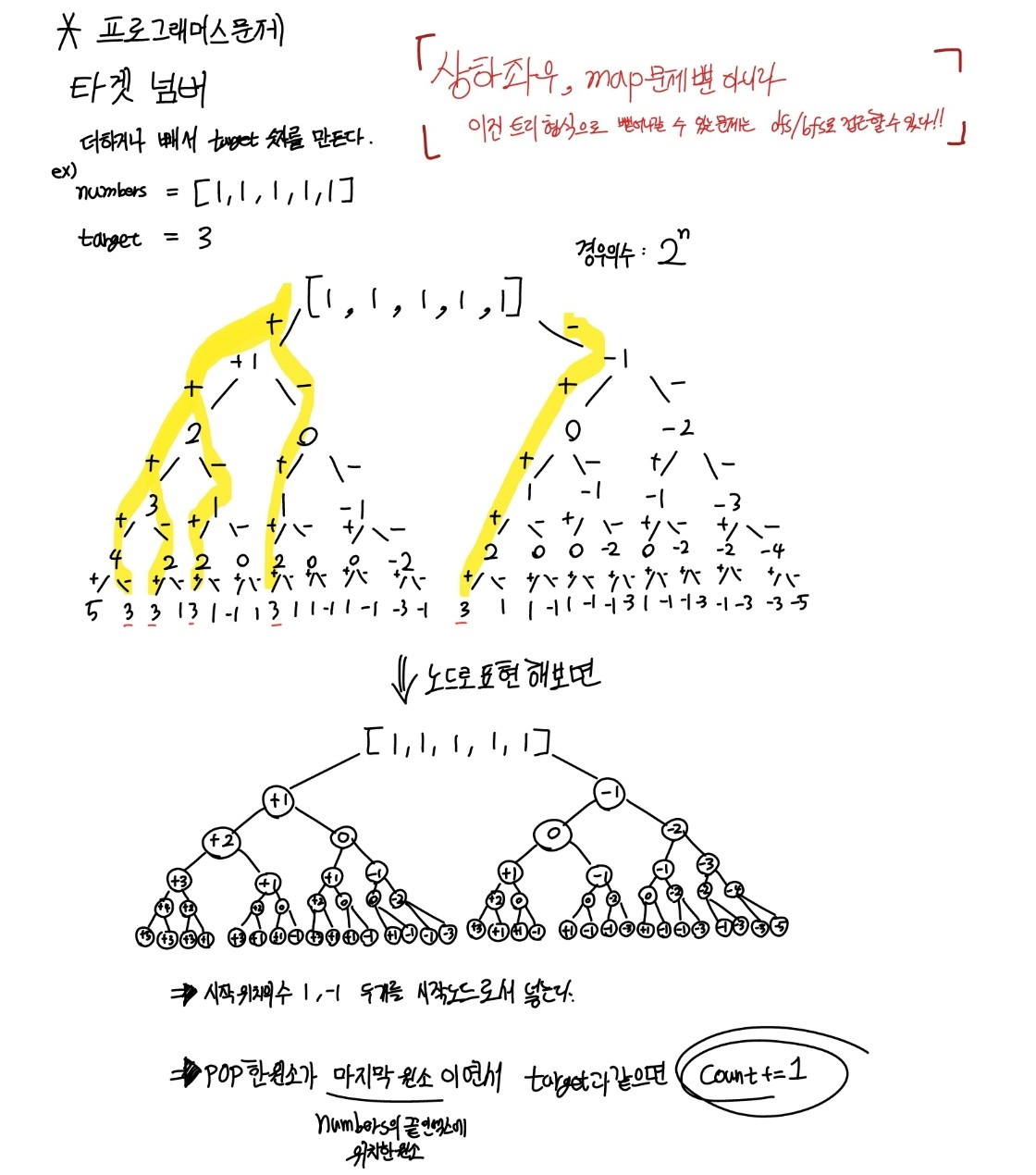
큐 자료구조를 이용하는 BFS 방법으로 풀었고, pop한 원소가 마지막 원소이면서 이것이 target과 같으면 count를 1더하는 식으로 문제를 풀 수 있었다.

완전탐색이 아니라 BFS를 사용하여 풀었을 때, 시간초과가 나지 않고 더 빠르게 동작할 수 있는 이유는 이미 계산한 값을 재활용하여, 같은 상태에 대한 중복 계산을 방지하기 때문인 것이 클 것이다. 이에 대해 다이나믹 프로그래밍을 처음 배울 때 들었던 설명이 떠올랐는데, 피보나치수열을 계산하는 프로그램에 대해 모든 경우의 수를 다 계산하지 않고, 이전 계산값을 사용하여 훨씬 빠르게 동작할 수 있었던 것과 같은 이유일 것이다.

from collections import deque

def solution(numbers, target):
    count = 0
    length = len(numbers)
    queue = deque()
    queue.append((numbers[0], 0))
    queue.append((-numbers[0], 0))
    while queue:
        number, idx = queue.popleft()
        if idx == len(numbers) - 1 and number == target: # 마지막인덱스이면서 target과 같으면
            count += 1
        else:
            if idx < length - 1: # numbers의 마지막 인덱스를 초과하지 않는다면
                idx += 1
                queue.append((number+numbers[idx], idx))
                queue.append((number-numbers[idx], idx))
    return count