MATHEMATICS FOR MACHINE LEARNING (Deisenroth, M. P., Faisal, A. A., & Ong, C. S. (2020)) 을 바탕으로 작성되었습니다.
이진 분류 문제의 경우 차원 D를 갖는 feature vector들을 두개의 숫자(e.g., +1, -1) 로 mapping하는 적절한 함수 를 찾는 문제라고 할 수 있다.
적절하다는 것은 각 에 해당하는 정답 이 있을 때, 다음과 같이 pair들로 구성된 set에 대해서 높은 정답률을 갖는다는 것이다.
그리고 이러한 task에 대해서 적절한 를 찾는 방법론 중 하나가
Support Vector Machine 이다.
Separating Hyperplanes
많은 classification algorithm의 아이디어는 공간을 적절하게 나눠서 같은 partition의 data들에게 같은 label을 할당하는 것 이다.
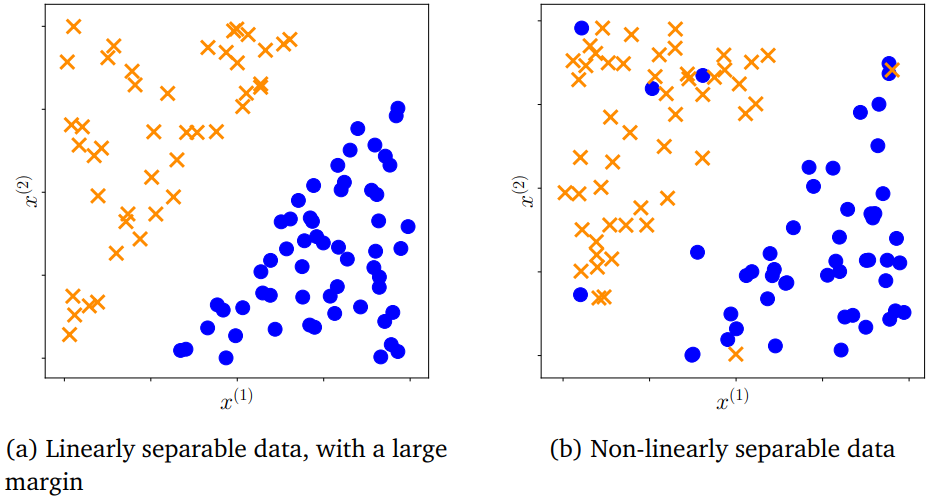
D = 2일때의 예시는 다음 그림과 같다.
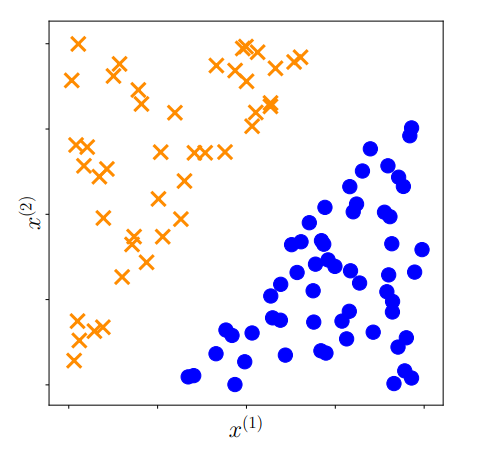
위 그림과 같은 경우, 직선 하나로 나뉘는 partition을 통해 두 class를 잘 분류할 수 있음이 명확하다.
마찬가지의 binary classification 문제에 대해 linearly splitting하는 경우, 인 공간에서는 두개의 partition을 만드는 평면을 생각할 수 있고
일반적으로 인 경우는 적절한 hyperplane을 고려할 수 있다.
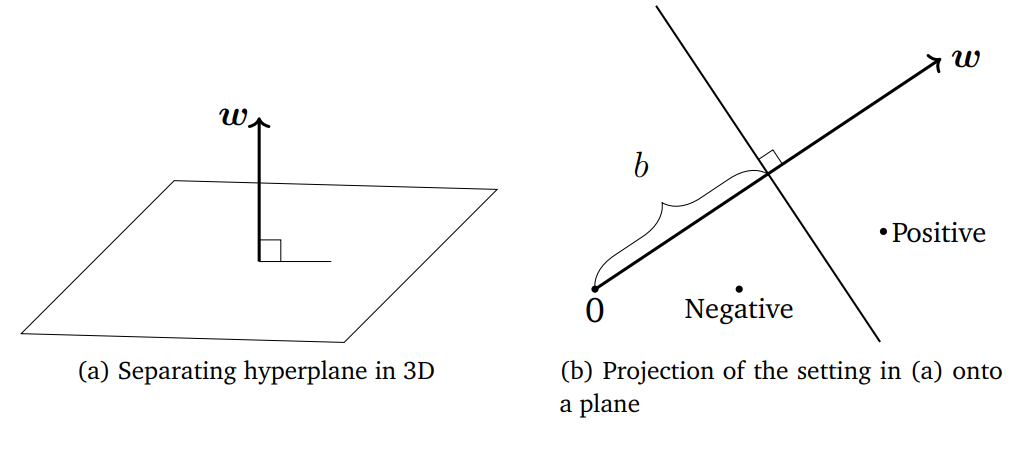
feature vector 들이 Projection 되었을 때 같은 class끼리 잘 나뉘는 방향벡터 가 있다면, 해당 를 normal vector로 갖고 b만큼 방향으로 translation한 hyperplane =0을 생각할 수 있다.
그리고 당연하게도 hyperplane위의 임의의 벡터는 와 orthogonal하다.
pf.
이므로
hyperplane의 기하학적인 의미를 생각해보면 ,
일 때,
일 때,
가 되도록 학습 시키는 것이 목적이다.
위 두 식은 하나의 식 로 나타낼 수 있다.
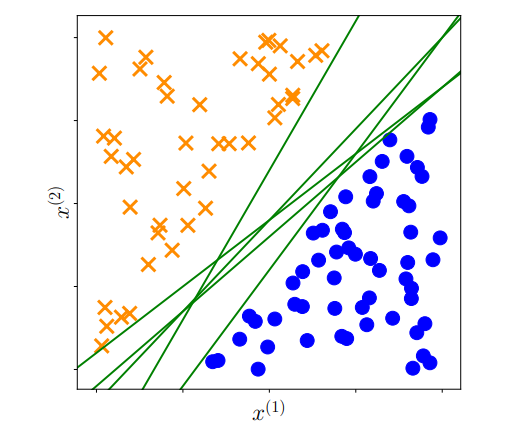
상술한 관점에서 두 class를 구분짓는 가능한 hyperplane은 위 그림처럼 무수히 많을 수 있다.
무수히 많은 hyperplane 중에서 우리가 원하는 좋은 hyperplane이란 margin을 최대화시키는 hyperplane이다.
margine이란 hyperplane과 가장 가까운 feature vector 사이의 거리이다.
Concept of the Margin
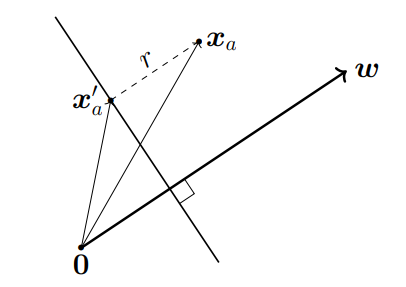
이고 이라면 ,
이므로
hyperplane이 적어도 r만큼의 margin을 갖는 상황으로 해석해서
로 적을 수 있다.
즉, 이라면, 다음과 같은 제약조건을 만족시키는
의 최대값을 찾는 문제가 된다.
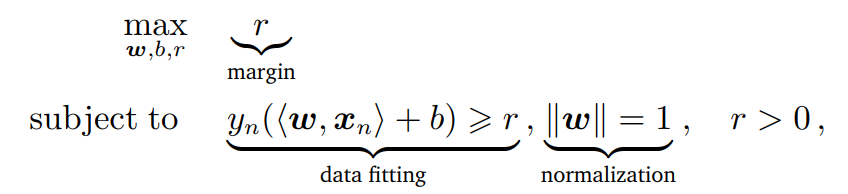
Hard Magin SVM
라는 normalization 가정을 주지 않았을 경우 margin maximazation problem이 어떻게 되는지 살펴보자.
normalization 가정 대신에, cloest data의 거리가 이 되도록 data의 scale을 변화시키는 가정을 주자.
즉, 다음과 같이 묘사할 수 있다.
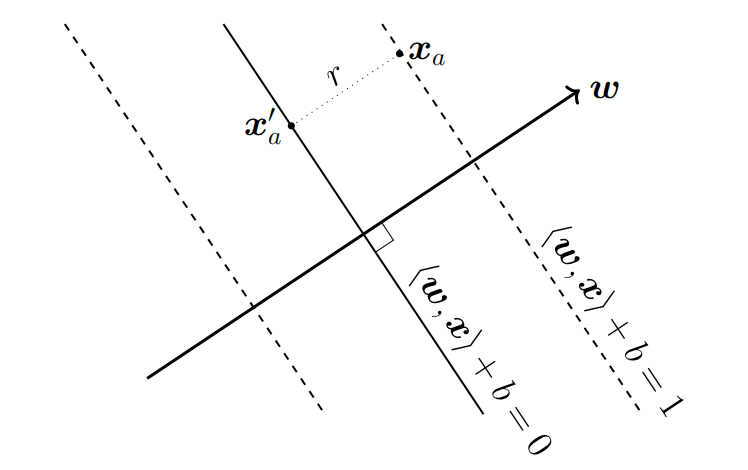
유사하게, hyperplane이 적어도 1만큼의 margin을 갖는 상황으로 해석해서
로 적을 수 있다.
즉, 다음과 같은 제약조건을 만족시키는
의 최대값을 찾는 문제가 된다.
일반적으로 다음과 같이 동등한 문제로 바꾼다.
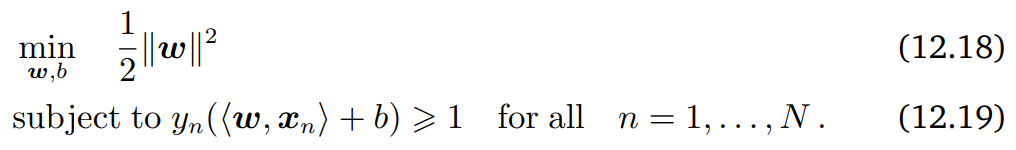
1/2 constant 는 gradient 계산의 편의를 위한 것이다.
식 (12.18)을 hard margin SVM이라고 하고 "hard"의 의미는 1보다 같거나 크다는 condition을 침범할 수 없기 때문이다.
만약 data의 분포가 linearly separable 하지 않다면 , hard condition을 완화시켜서 soft condition을 갖는 문제로 바꾼다.
Soft Margin SVM : Geometric View
soft condition으로 완화된 SVM을 soft margin SVM 이라고 한다.
기하학적인 관점에서 먼저 살펴보자.
각각의 에 대응되는 을 hard margin SVM condition
에서 빼주면 각각의 feature vector는 1 보다 만큼 작은 거리만큼 hyperplane으로 부터 떨어져도 되게 된다.
양수인 이 1 보다 클 수 있으므로 다음 그림과 같이 잘못된 partition에 속한 feature vector인 경우도 허용할 수 있게 된다.
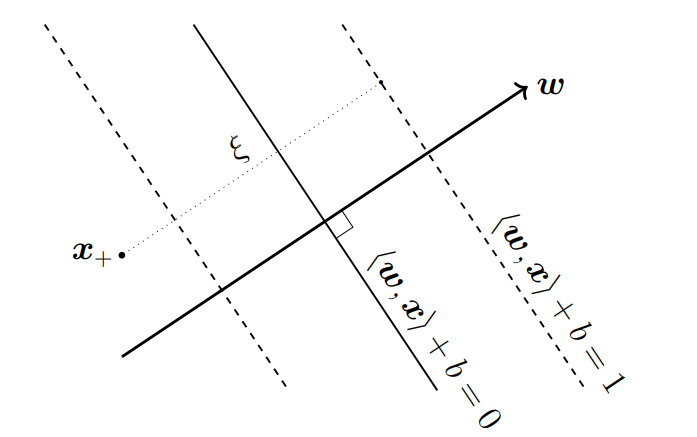
들도 최소화되어야 좋은 최적화이므로 Objective function은 다음과 같다.
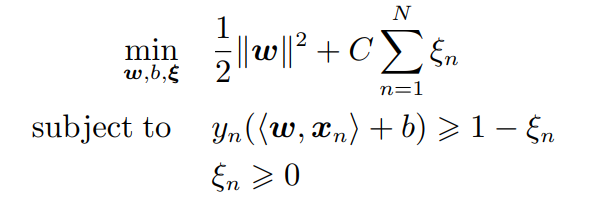
linearly separable 한 상황이라면, = 0 인 경우가 이상적으로 optimize된 상황일 테니 해당 경우는 hard margin SVM의 경우와 같아진다.
이 경우 해당 objective function의 는 L2 regularization으로 볼 수 있다.
다만 b의 경우는 regularized 되지 않았기 때문에 이경우 theoretical analysis는 복잡하다.
Soft Margin SVM : Loss Function View
위에서 언급한대로 를 regularzation으로 본다면, 대응 되는 Loss function은 무엇일까?
binary classification문제에서 Loss function은 label과 prediction이 틀린 수와 관련되어 있어야 할 것이다.
따라서 prediction에 해당하는 과 label에 해당하는 이 일치하면 0, 다르면 1을 출력하는 zero-one loss function을 생각할 수있다.
하지만 zero-one loss function을 optimize하는 문제는 이산공간에서 최적의 해를 찾는 (e.g., Traveling Salesman Problem (TSP)) Combinatorial optimization problem 이기 때문에 일반적으로 continuous optimization problem에 비해 어렵다. (많은 Combinatorial Optimization Problem이 NP-hard problem 이다.)
따라서 hinge loss를 사용한다.
hinge loss는 다음과 같다.
where
만약 prediction과 y가 일치하고, 기하학적으로 hyperplane으로 부터 거리가 1 이상 떨어져 있다면, 이므로 t=0 이고 이다.
prediction과 y가 일치하지만, 기하학적으로 떨어진 거리가 1 미만이라면 0 < t < 1 이고 작은 값 을 갖는다.
반면에 prediction과 y가 다르면 t < 0 이고 큰 값 을 갖는다.
이상적으로 , hinge loss = 0 이 되도록 optimize한다는 것은 margin 내의 어떠한 feature vector도 위치시키지 않겠다는 것이므로
이전에 언급한
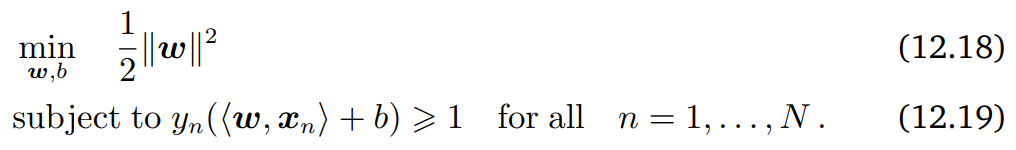
hard margin SVM 문제를 푸는 것과 동등하다.
하지만 다음과 같이 제약조건이 없는 optimization problem이 된다.
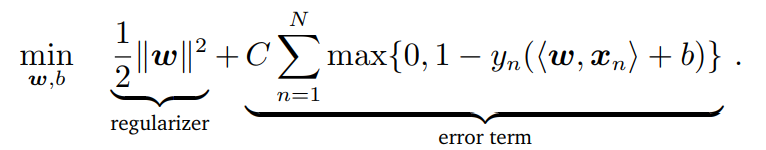
그리고 이것은 Geometric View에서 논의했던 를 도입한 optimization problem을 상기해봤을 때 단순히 수식적으로
error term를 optimize하는 것에 해당하는 푼다는 것이
subject to 를 푸는 것과 동등하다는 것을 알 수 있다.
Dual Support Vector Machine
위에서 살펴 본 SVM 들은 모두 primal SVM에 속한다. 이제는 동등하지만 dual view로 바라본 optimization problem에 대해 이야기 해보자.
간단히 말해서, optimization theory에서 최소값을 찾는 primal problem과 동등한 dual problem이란 최대값을 찾는 문제이다.
라그랑주 승수법을 통해 dual problem으로 변환된다.
https://en.wikipedia.org/wiki/Duality_(optimization).
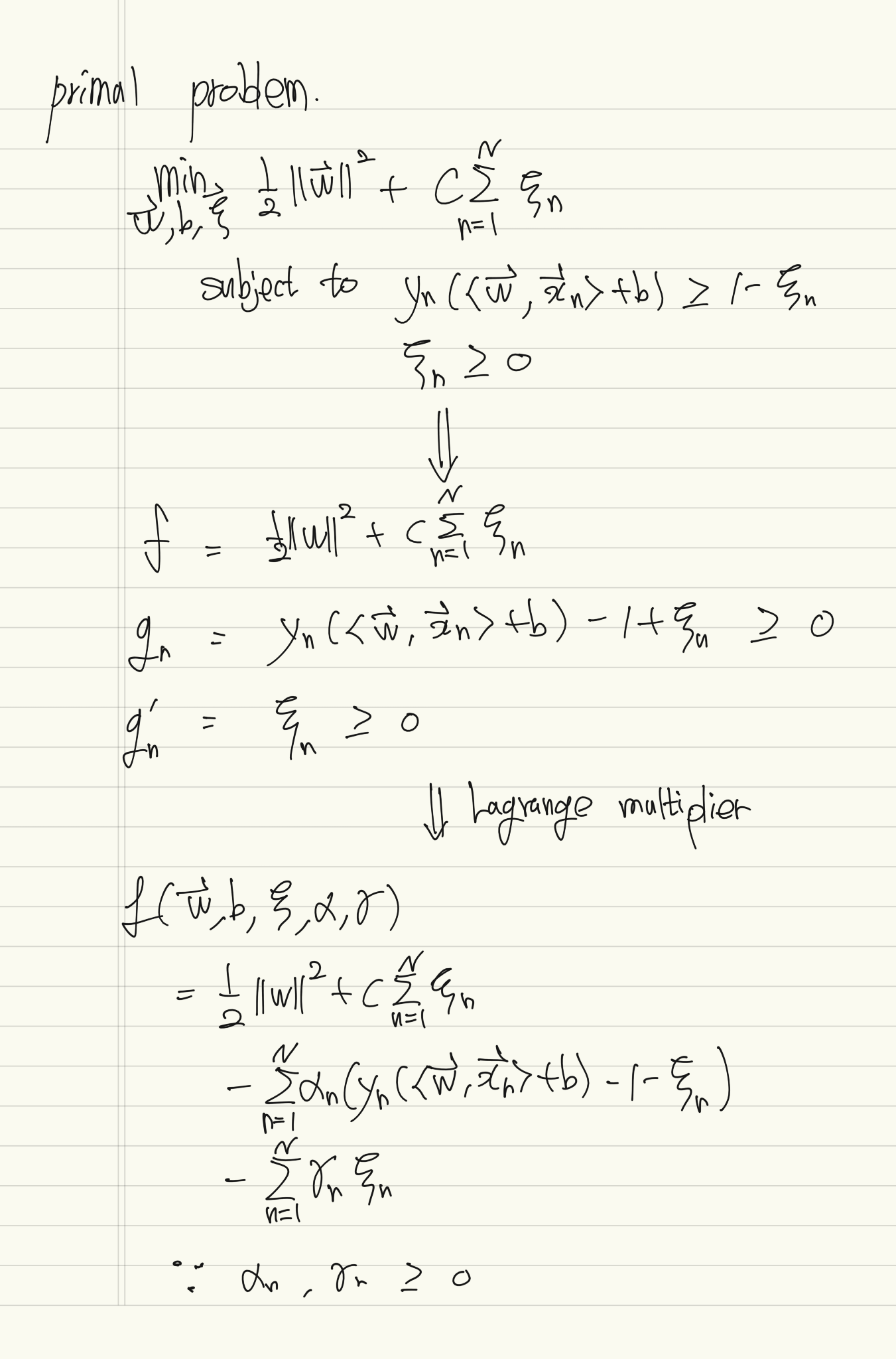

0이 아닌 과 대응되는 는 hyperplane을 만드는데 도움을 주기 때문에 "support vector"라고 한다.


같은 부등식 형태의 제약조건은 SVM에서 "box constraint" 라고 한다. 해당 조건은 KKT condition을 통해 유도될 수도 있다.
Optimal 의 값은 Numerical Solvers로 푸는 것이 효율적이다.
Numerical Solver에 대해서는 다음 책의 Chap 5. Bound constrainted minimization를 참고할 것.
Dostal, Zden ´ ˘ek. 2009. Optimal Quadratic Programming Algorithms: With Applications to Variational Inequalities.


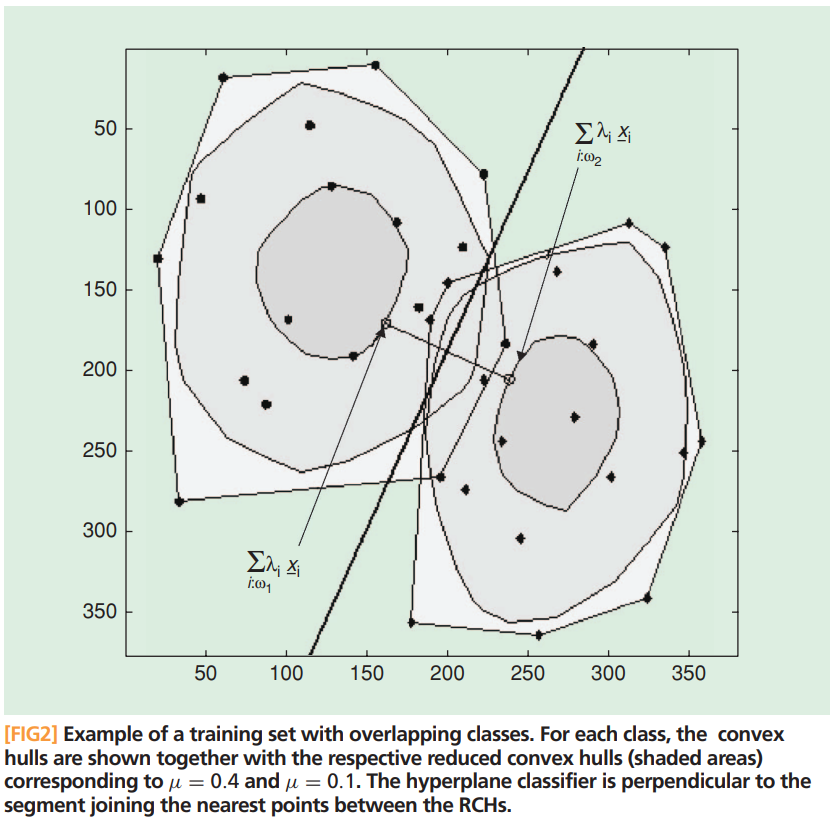
Dual SVM: Convex Hull View
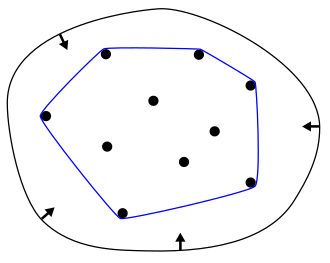
convex hull 이란 아래 그림과 같이 partition의 점들을 포함하는 최소 크기 둘레의 다각형이다. 폐곡선 고무줄을 줄이는 것을 통해 만들어짐을 쉽게 상상할 수 있다.
convex set 이란 같은 label의 모든 feature vector들을 포함하는 smallest possible set이다.
라그랑주 승수법말고 Dual SVM를 유도하는 다른 접근법에 대해서 이야기해보자.




Dual SVM with kernels
위에서 살펴본 subject to 문제는 에 대한 optimization이므로 내적 을 다르게 바라보자.
일반적으로, 이다.
하지만 두 사이의 identity matrix 대신 "positive-definite"한 matrix가 들어가더라도 내적의 정의를 만족하므로 이때의 임의의 positive-definite matrix를 kernel matrix 라고 하고 로 내적을 정의하자는 것이 kernel의 아이디어 이다.
다만 SVM에서 kernel 방법을 묘사할 때, 일반적인 표현은 를 로 바꾸지않고 의 표현을 바꿔서 라고 적고 이때의 를 non-linear feature map , 를 kernel 이라고 한다. 는 hilbert space를 의미한다.
feature map 는 입력에 해당하는 feature vector를 더 높은 차원으로 mapping 할 수 있는데 이는 일반적으로 hilbert space로 mapping 한다고 할 수 있다. hilbert space에서 알 수 있듯이 이론적으로 infinite dimension으로의 mapping을 함의한다.
내적의 정의.
연산 이 다음 세 성질을 만족하면 내적이라 한다.
1. symmetry :
2. Liniearity (in the first argument) :
2-1 : =
2-2 : = +
3. Positive - Definiteness : ,
참고로 Hermitian matrix & positive eigenvalue Positive-definite matrix
https://en.wikipedia.org/wiki/Definite_matrix
Polynomial kernel
예를 들어, feature vector들의 차원이 2인 경우의 polynomial kernel과 그것에 대응되는 feature map은 다음과 같다.

Gaussian kernel
Radial Basis Fuction (RBF) kernel 이라고도 부른다.
gaussian kernel의 경우는 feature map이 feature vector를 infinite dimension으로 mapping한다는 사실을 확인할 수 있다.


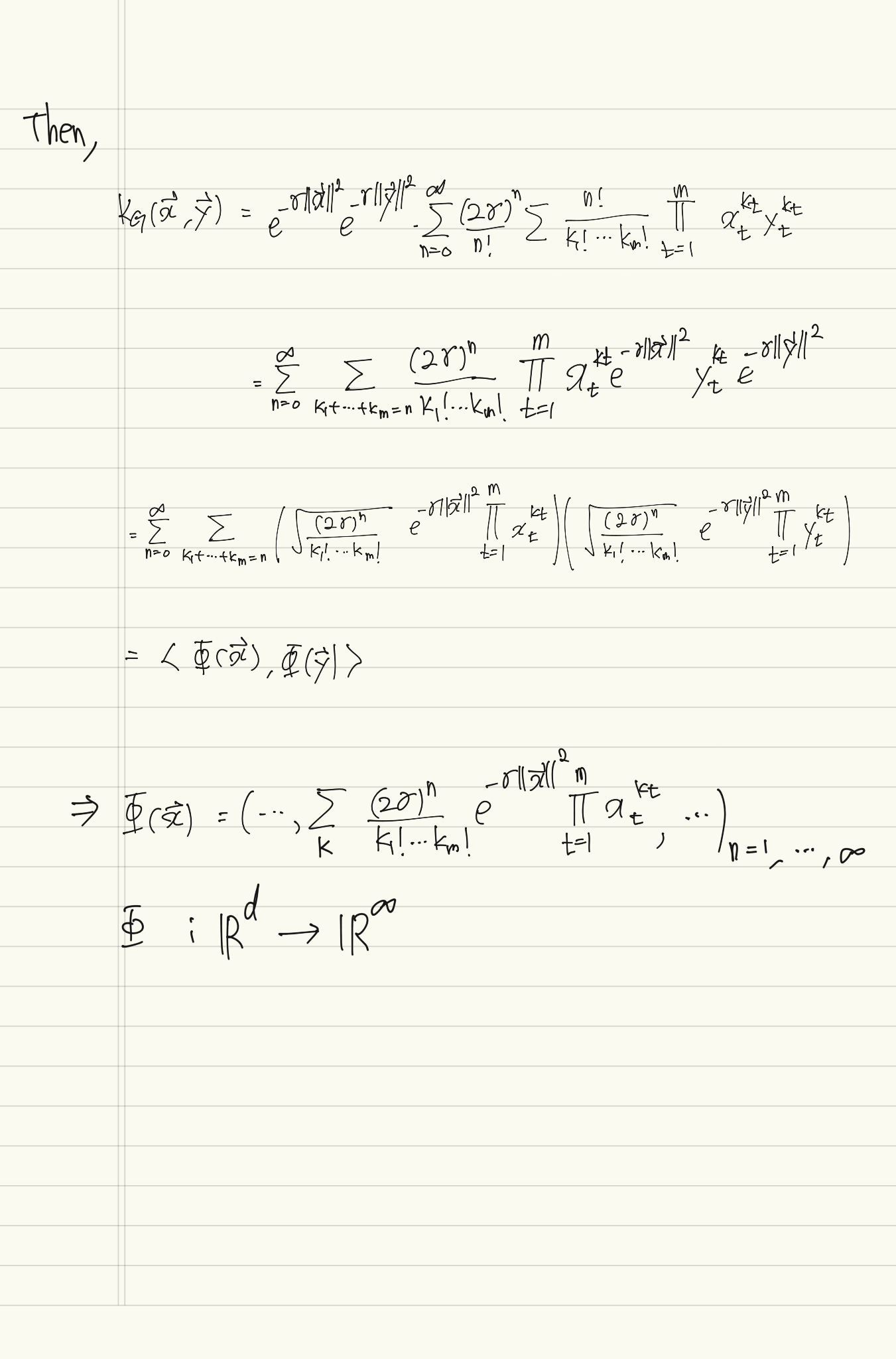
infinite dimension을 갖는 feature map을 계산하는 것은 불가능하지만 단순한 gaussian kernel 를 계산함으로써 infinite dimension을 고려할 수 있기 때문에 kernel의 강력함을 느낄 수 있다.
Gaussian kernel map의 증명과정 참고자료.
The intuition behind kernel methods
위 과정과 상이한 부분이 있어서 주의바람.
효율적인 kernel의 parameter와 kernel의 선택에는 nested cross-validation을 통해 이루어진다.
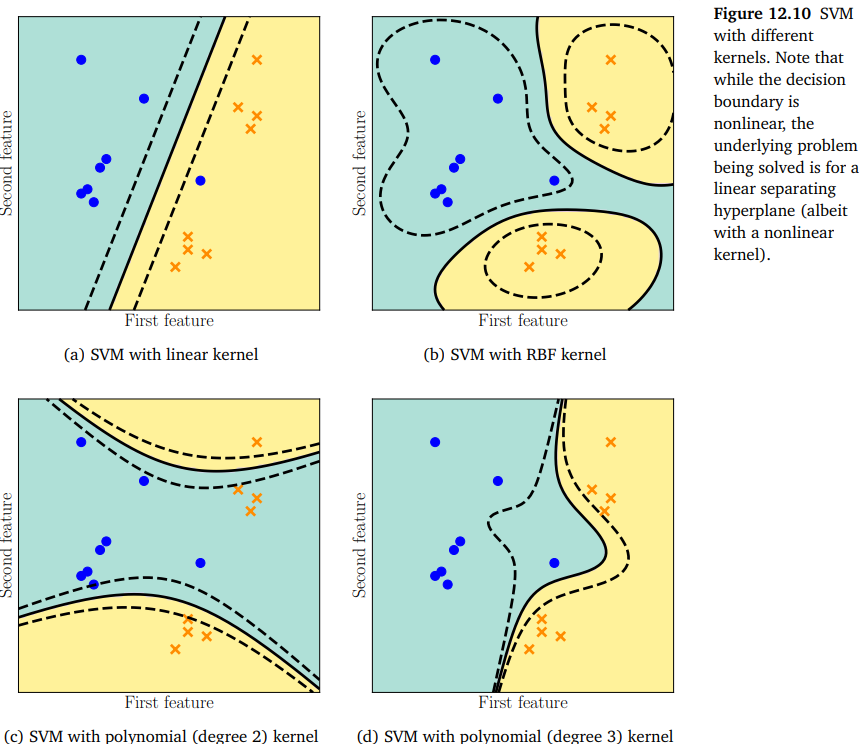
feature map 를 통해서 feature vector 를 hyperplane으로 linearly separable한 높은 차원으로 mapping 한다고 생각 할 수도 있고 반대로 아래 그림과 같이 는 동일한 공간에 위치하고있고 hyperplane을 non-linear하게 변환한다고 여길 수 도 있다.