Information Bottleneck Principle

Objective

DNNs에 대해 새로운 이론적 해석을 제시한다.
Layer들간의 Mutual Information을 통해 DNNs를 정량화하고 기하급수적으로 많은 DNNs의 parameter때문에(VC dimension 값이 매우 큼) 좋지않은 Bound가 되는 traditional learning theory의 Generalization Bounds대신 새로운 Bounds를 제시한다.

Approach

supervised learning의 목표는 결국 output과 연관된 정보를 input으로 부터 효과적으로 뽑아내는 것에 있다.

layered 된 DNNs의 구조를 연속적인 Markov chain 과정(이전 layer에만 의존성을 갖는 = Markov property = memoryless property)으로 바라보자.

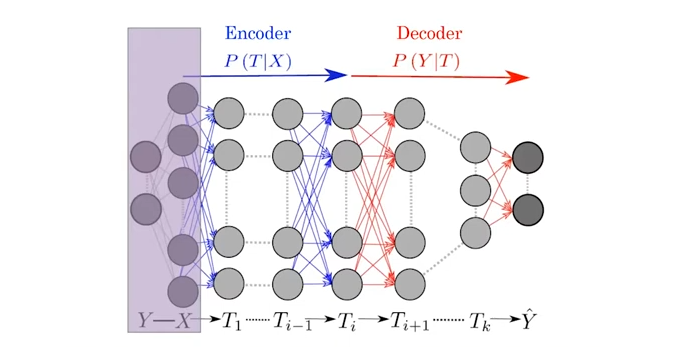
$X$ : input
$Y$ : desired output
$T$ : the representation of hidden layer

여기서 $T$는 Disentangled, Interpretable, useful for predicting $Y$ 해야 좋은 $T$라고 할 수 있다.
Disentangled : X의 다른 property들이 T를 구성할 때 서로 다른 component여야 한다.

DNNs는 Training 과정을 통해 $X$의 optimal representation을 찾는다고 할 수 있다. Optimal representation of $X$란 $Y$에 irrelevant information은 제거하고(compression) relevant information은 capture해서 $T$를 구성하는 것이다.

예를 들어,

고양이 이미지$X$에서 DNNs를 통해 extraction된 feature $T$가 있고
고양이 인지 아닌지 판별하는 TASK라고 했을 때
$T$에서 relevant information은 "cat"이고 irrelevant information은 "laptop"이다.

$X$와 $Y$가 statistical dependency를 갖는다고 가정했을 때,
relevant information의 정도는 mutual information $I(X,Y)$로 정의된다.
( $I(X,Y)$ = 0 $\rightarrow$ $X,Y$ are independent, irrelevant )

통계학에서,
A representation $S(X)$ of $X$ is sufficient statistics for $Y$ $\Leftrightarrow$
$I(S(X);Y) = I(X;Y)$
$S(X)$가 $X$로부터 $Y$와 관련된 정보를 모두 담고있다고 할 수 있다.

A representation $T(X)$ is minimal sufficient statistics of $X$ with respect $Y$
$\Leftrightarrow$ $T(X) = argmin(I(S(X),X))$
; $S(X):I(S(X);Y)=I(X;Y)$
$T(X)$는 $Y$와 관련된 정보를 모두 담고 있는 sufficient statistics이면서 동시에 $X$에 대한 정보는 최소한으로 담고 있다고 할 수 있다.

Information Bottleneck Principle에 따르면,
Optimal representation of $X$는 다음과 같이 minimal sufficient statistics인 $T(X)$를 이용해서 정의된 $\mathcal{L}$( functional, Lagrangian )을 minimization함으로써 찾게된다.
$\mathcal{L}[p({\hat x}|x)] = I(X;T) - \beta I(T;Y)$

즉, Training이란 hidden layer의 representation이 input $X$에 대한 정보는 덜어내고 desired output $Y$과 관련된 정보는 최대한 담는 과정이라고 해석할 수 있다.

Training이 feature space의 차원을 줄이는 effective feature dimension를 찾는다는 관점(nonlinear feature dimensionality reduction)에서 $I(X;T)$는 "the complexity (rate) of the representation"라고 표현할 수있고
$I(T;Y)$는 상술했듯이 desired output $Y$과 관련된 정보는 최대한 담는 과정이기때문에 "the amount of preserved relevant information" 이라고 표현할 수 있다.

이렇게 표현했을 때, $\beta > 0$ (positive lagrangian multiplier)는 "the complexity (rate) of the representation"와 "the amount of preserved relevant information"를 tradeoff하는 parameter라고 할 수 있다.
$\mathcal{L}$이 optimize되는 동일한 값에 대해서 $\beta$가 클수록 "the amount of preserved relevant information"이 작아지고 "the complexity (rate) of the representation"는 커지기 때문으로 추측된다. (사실 $\beta =1$ 인 경우가 special case고 $\beta = \cdot$ 인 경우가 general하다.)

Conclusion

References

https://arxiv.org/pdf/1503.02406.pdf
https://arxiv.org/pdf/1703.00810.pdf
https://www.youtube.com/watch?v=-SX3vbZfRhg
https://horizon.kias.re.kr/18474/
https://lilianweng.github.io/posts/2017-09-28-information-bottleneck/