마코프 결정과정(MDP, Markov Decision Process)

마코프 결정과정(MDP, Markov Decision Process) 은 마르코프 보상과정(MRP, Markov Reward Process)에 행동(A: Action)과 정책($\pi$: Policy)이 추가된 개념이다.

• MRP의 목적 : 에피소드나 환경전체의 가치를 계산
  • 에이전트는 타임스텝에 따라 상태전이확률(P)에 영향을 받으며 자연스럽게 이동한다.

• MDP의 목적 : 환경의 가치를 극대화 하는 정책을 결정하는 것
  • MDP에서는 에이전트(Agent)라는 새로운 개념이 등장한다. MDP에서는 에이전트가 취한 행동과 상태 전이 확률의 영향을 동시에 받아 환경의 상태가 바뀐다.
  • MDP에서 에이전트는 정책($\pi$)에 따라 행동(A)을 하며 상태(S)는 에이전트가 취한 행동과 상태전이확률(P)에 따라 바뀌게 된다.
• MDP의 구성요소
  • $S$ : 상태(State)의 집합
  • $P$ : 상태 전이 매트릭스
    $P^a_{ss'} = P[S_{t+1} = s' | S_t = s, A_t = a]$
    시간 $t$에서 상태가 $s$ 였을 때 $a$ 행동을 할 경우 시간 $t+1$ 에서 상태가 $s'$ 일 조건부 확률
    
  • $R$ : 보상함수
    $R_s^a = E[R_{t+1}| S_t = s, A_t = a]$
    간 $t$에서 상태가 $s$ 였을 때 $a$ 행동을 할 경우 시간 $t+1$ 에서 받는 보상의 기댓값
    
  • $\gamma$ : 감가율
  • $A$ : 행동(Action)의 집합
  • $\pi$ : 정책 함수

MDP는 MRP의 상태전이매트릭스와 보상함수에 ‘행동’이라는 조건이 더 추가됐다. MDP에는 행동(A)이 추가됐기 때문에 상태 전이 매트릭스와 보상함수 또한 행동을 함께 생각해줘야 한다. MDP에서 취할 수 있는 행동의 개수는 상태와 마찬가지로 유한하다.

MDP에서 정책이란?
$\pi = P[A_t = a | S_t = s]$

MDP에서 정책이란 행동을 선택하는 확률이다. 따라서 정책에서 따라 행동한다는 것은 확률이 높은 행동을 할 가능성이 크다는 의미이다.

MDP에서 에이전트는 항상 정해진 길을 따라가진 않는다. 언제나 의외성이 존재한다. 이는 이후 나올 탐험(Explopration)과 연관이 있다.

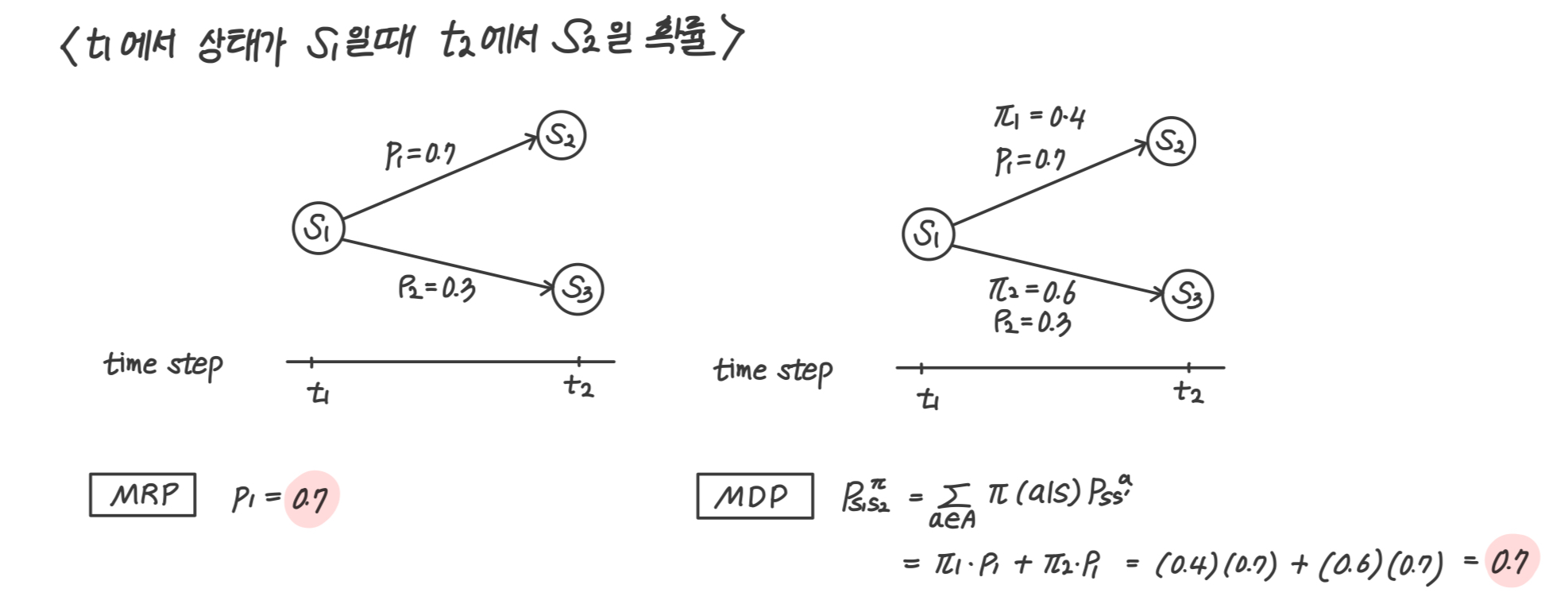
위를 보면 정책의 확률과 그쪽으로 이동할 확률을 곱해줘서 다 더한다. 에이전트는 s2로 가는 a1과 s3로 가는 a2중 하나를 고를 수 있다. 에이전트가 정책에 따라 a1을 선택했다고 하더라도 반드시 s2로 이동하지 않는다. 바로 상태전이 확률에 영향을 받기 때문이다.

상태전이확률은 에이전트의 의지와 전혀 상관없는 환경에서 자연적으로 발생하는 환경이다. 따라서 정책에 대한 확률과 상태전이확률을 각각 곱해서 더해야 한다.

MRP나 MDP나 s1에서 s2로 이동할 확률은 동일하다. 그러나 MDP는 정책이라는 새로운 요소가 추가된 것이고 이 덕분에 새로운 기능을 추가할 수 있다.

MDP에서 에이전트의 행동은 오로지 정책에 의해 결정되며, 정책은 시간에 따라 변하지 않는다. MDP도 마코프 속성을 가정하므로 현재상태에만 영향을 받는다.

• 정책을 고려한 상태 전이 매트릭스와 보상 함수
  
  $P_{ss'}^\pi = \sum_{a \in A} \pi(a|s)P_{ss'}^a$
  $R_s^\pi = \sum_{a \in A}\pi(a|s)R_s^a$

정책도 매트릭스 형태의 조건부 확률이다. MDP에서 상태가 변한다는 것은 원래 가지고 있던 상태 전이 매트릭스와 정책의 영향을 동시에 받는다는 것이다.

따라서 행동에 따른 정책과 상태전이확률의 기댓값을 구함으로써 정책을 고려한 상태전이매트릭스를 구할 수 있다.

정책을 고려한 보상함수 또한 상태전이매트릭스와 동일하게 정책과 각 행동별 보상 함수의 기댓값을 통해 나타낸다.

MRP와 MDP의 상태 가치 함수

• MRP의 상태가치함수
  $v(s) = E[R_{t+1} + \gamma v(S_{t+1}) | S_t = s] \\ = R_{t+1} + \gamma E[v(S_{t+1})|R_t = s] \\ = R_{t+1} + \gamma \sum_{s' \in S}p_{ss'}v(s')$
• MDP의 상태가치함수
  $v_\pi(s) = E_\pi[R_{t+1} + \gamma v_\pi(S_{t+1})|S_t = s] \\ = \sum_{a \in A} \pi(a|s)(R_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_\pi (s')) \\ = \sum_{a \in A}\pi(a|s)R_s^a + \gamma\sum_{a \in A}\pi(a|s)\sum_{s' \in S}P_{ss'}^a v_\pi(s')$

MRP와 MDP의 상태 가치 함수는 같다!

두 값은 같지만, MDP에서 상태 가치 함수를 구할 때는 정책이라는 요소를 하나 더 고려한 것뿐이다.

MDP 행동 가치 함수(Q 함수)

MDP의 목적은 환경의 가치를 극대화하는 정책을 결정하는 것이다. 그리고 정책은 행동을 결정하는 확률이다.

상태 가치 함수는 상태를 중심으로 가치를 평가했다. 정책을 평가하기 위해서는 ‘행동’을 중심으로 평가해야 한다. 이것이 바로 행동 가치 함수(Q : Action Value Function, Q함수)이다.

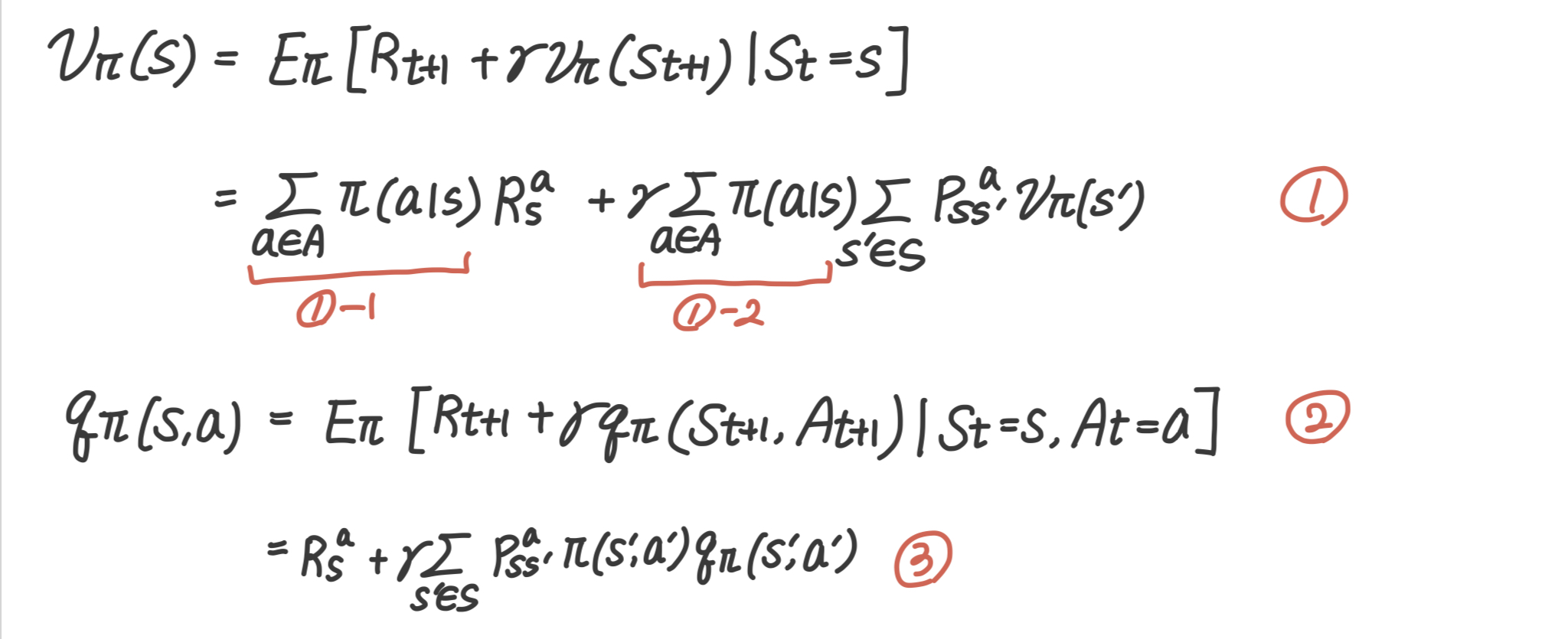
1번은 상태가치함수를 다시 기술한 것이다. 행동가치함수에서는 행동을 미리 선택했기 때문에 기댓값을 구할 필요가 없다. 따라서 1-1과 1-2 부분을 빼고 수식을 3번과 같이 기술할 수 있다.

$\pi(s',a')$ 부분이 추가된 것은 다음 상태에서의 보상을 정확히 계산하기 위해서는 정책과 상태 전이 확률 매트릭스를 곱해줘야 하기 때문이다.

Q함수는 선택할 수 있는 여러 행동 중 하나를 선택했을 때의 가치를 계산한다.

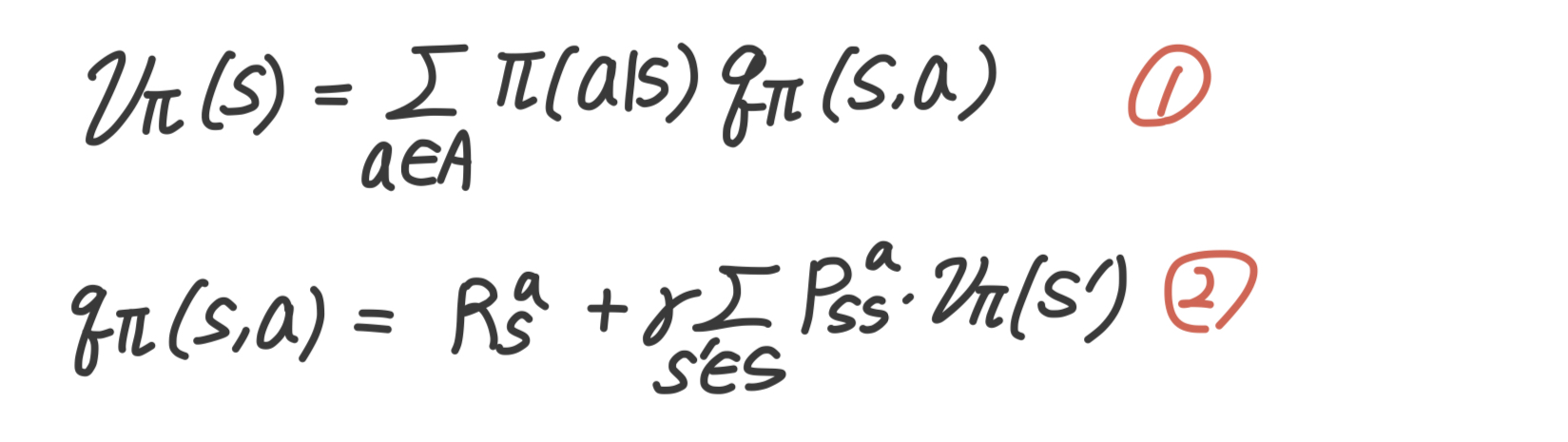
행동 가치 함수 $q_\pi (s,a)$는 내가 선택한 행동의 가치를 계산하는 함수이고, 상태 가치 함수 $v_\pi(s)$는 특정 상태의 가치를 계산하는 함수이다.

1. MDP에서 하나의 상태에서 다른 상태로 이동하기 위해서는 상태 전이 매트릭스와 함께 행동을 선택할 확률인 정책을 함께 고려한다. 따라서 행동 가치 함수를 사용해서 상태 가치 함수를 구하기 위해서는 정책에 대한 기댓값을 구한다.

2. 행동 가치 함수는 어떤 행동을 했을 때 그 가치가 어떻게 되는지 계산한 것이다. 가치는 현 상태에서 즉시 받을 수 있는 보상 + 미래에 받을 수 있는 보상으로 계산한다. 미래 보상은 행동을 했을 때 이동한 상태에 따라 달라진다.

   $P_{ss'}^a$ → 상태 전이 매트릭스에서 모든 행동을 고려하는 것이 아니라 하나의 행동만을 고려한다.

MDP는 가치를 극대화 하는 것이 목표이다. 가치를 기반으로 정책을 평가해서 가치를 최대화하는 정책(최적 정책 : Optimal Policy)를 찾는 것이 최종적인 목적이며, 이것이 강화학습의 기초적인 개념이다.

MDP 최적 가치 함수

이제 MDP의 최종목적을 달성하기 위해 최적 가치 함수(Optimal Value Function)에 대해 알아보자.

최적 가치 함수는 아래처럼 최적상태 가치함수와 최적행동 가치함수로 나눌 수 있다.

1. 최적 상태 가치함수 : 여러 정책을 따르는 상태가치함수가 있을 때 가치를 최대로 하는 정책을 따르는 상태 가치 함수를 말한다.
2. 최적 행동 가치 함수 : 다양한 정책을 따르는 행동 가치 함수 중에서 가치를 최대로 하는 정책을 따르는 행동 가치 함수를 말한다.

MDP에서 최적 행동 가치 함수를 안다는 것은 가장 효율적인 행동을 선택할 수 있는 정책을 안다는 것과 같다. 따라서 최적 행동 가치 함수를 찾아내면 MDP 문제를 해결할 수 있다.

• 최적정책의 특성
  • $\pi^* : \pi^* \ge \pi, \forall pi$
  • $v_{\pi^*}(s) = v^*(s)$
  • $q_{\pi^*}(s) = q^*(s)$

• 최적 정책을 나타내는 방법
  
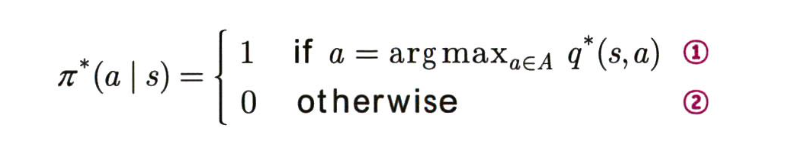
  어떤 행동 a가 최적 행동 가치 함수의 최댓값을 반환하게 만드는 행동이라면 그 행동에 대한 정책은 1이 되고, 그렇지 않으면 0이 된다.
  이때 정책은 행동을 선택할 수 있는 확률이므로 상태 s에서의 정책은 확률이 1로 설정된 행동을 반드시 선택하게 된다.