강화학습이란?
강화학습(RL, Reinforcement Learning) : 적절히 설계된 보상 체계를 활용해 에이전트가 긍정적인 행동을 할 수 있도록 에이전트 행동을 제어하는 정책을 찾아내는 최적화 기법
에이전트(Agent)는 정책(Policy)에 따라 어떤 환경 (Environment)에서 특정 행동(Action)을 한다. 그러한 행동에 따라 환경의 상태(State)가 바뀌고 상태가 긍정적으로 바뀌 었는지 부정적으로 바뀌었는지에 따라 보상(Reward)을 받는다.
- 강화학습 구성요소
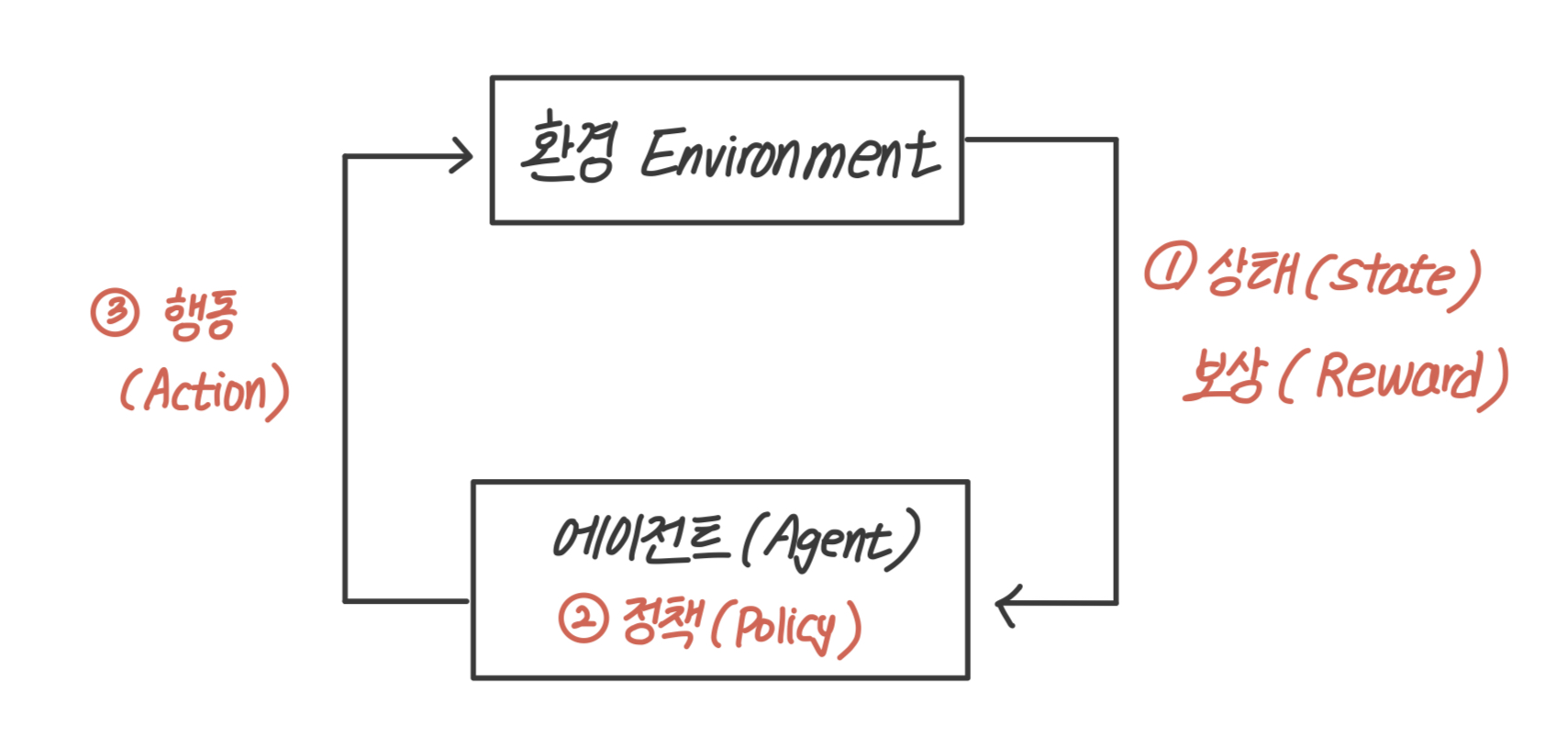
행동, 상태의 종류가 적은 경우에는 계산을 통해 최적의 정책을 찾을 수 있으나 상태의 종류가 많아질수록 최적의 정책을 찾는 계산 증가 → 인공신경망 활용
환경과 에피소드
환경과 에피소드라는 말이 계속 나온다. 환경(Environment)은 아래 그림처럼 각 노드(상태)와 엣지로 이루어진 전체를 의미하고, 에피소드(Episode)는 S > R1 > R3 > F 처럼 일련의 연속된 상테의 변화를 의미한다.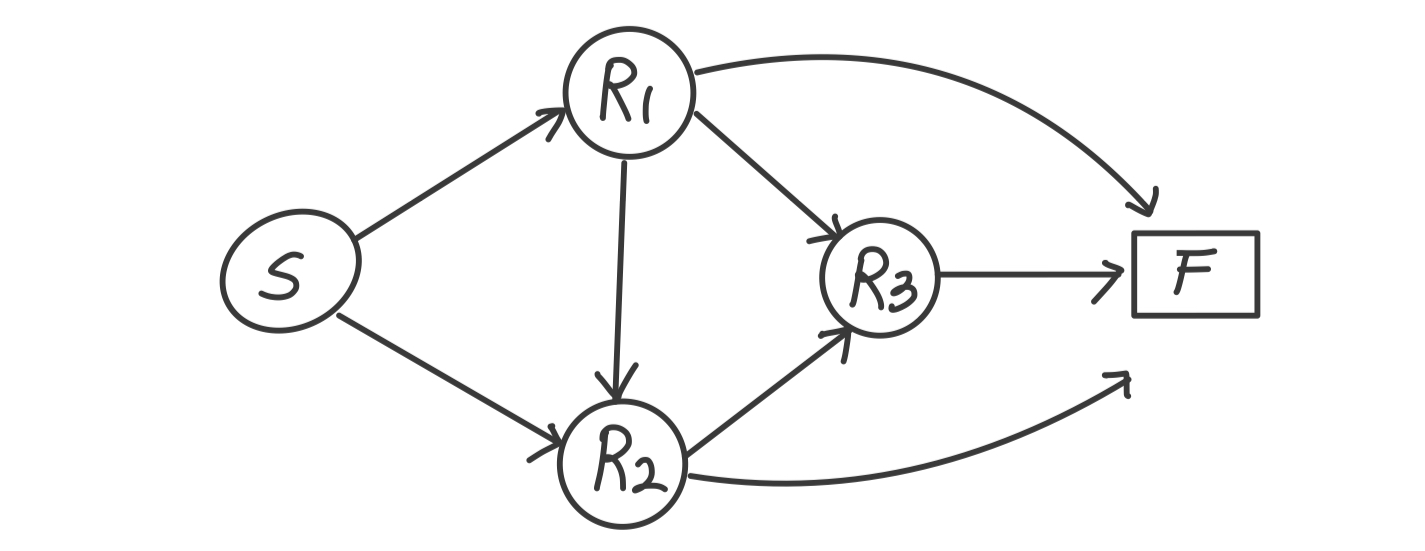
확률과 확률과정
- 확률적(stochastic)이다? = 무작위적 (random)이다!
📌 경영과학2에서 마코프 체인, 마코프 프로세스에 대해 자세하게 배운다. 마코프 프로세스를 넘어 대기행렬이론까지 배우는데 이 내용은 추후 블로그에 정리할 예정이다.
확률 과정(Stochastic Process)
시간의 흐름에 따라 확률적(무작위적)으로 움직이는 상태를 말한다.
로 집합으로 표현한다. X는 랜덤변수, t는 시간이다.
이런 확률 과정이라는 개념을 만들어 수학적으로 현상을 표현하면 프로그래밍을 통해 쉽게 문제 해결이 가능해진다.
마코프 속성(Markov Property)
마코프 속성은 확률과정의 특수한 형태로, memoryless, 즉 과거에 일어났던 일들과 무관하게 현재의 상황만이 미래의 상황에 영향을 미친다는 것을 의미한다.
이렇게 과거의 일을 무시하고 현재만을 고려하면 문제를 풀기 훨씬 수월해진다. 마코프 속성을 조건부 확률로 나타내면 아래와 같다. St는 t시점에서의 상태를 의미한다.
마코프 연쇄(Markov Chain)
마코프 체인(Markov Chain)은 마코프 속성을 지닌 시스템의 시간에 다른 상태 변화를 나타낸다. 즉, 과거와 현재 상태가 주어졌을 때, 미래 상태의 조건부 확률 분포가 과거 상태와는 독립적으로 현재 상태에 의해서만 결정되는 환경을 말한다.
- 시간이 이산적일 때 → Markov Chain 이라고 하며
- 시간이 연속적일 때 → Markov Process 라고 한다.
마르코프 보상 과정(MRP, Makov Reward Process)
MRP : 마코프 연쇄에 보상(Reward)과 시간에 따른 보상의 감가율인 감마()가 추가된 개념
마코프 연쇄 : 상태에 전이확률만 주어짐 → 상태변화가 얼마나 가치있는지는 알 수 X ↔ MRP는 상태변화의 가치까지 계산!
구성 : 상태집합(), 상태 전이 매트릭스(), 보상함수(), 감가율()
-
상태집합()
MRP에서는 상태는 유한!
-
상태 전이 매트릭스()
-
보상함수()
: 시간 t에서 상태가 s일 때, 시간 t+1에서 받을 수 있는 보상의 기댓값
보상함수(Reward Function)는 확률의 기댓값 형태로 표현할 수 있다.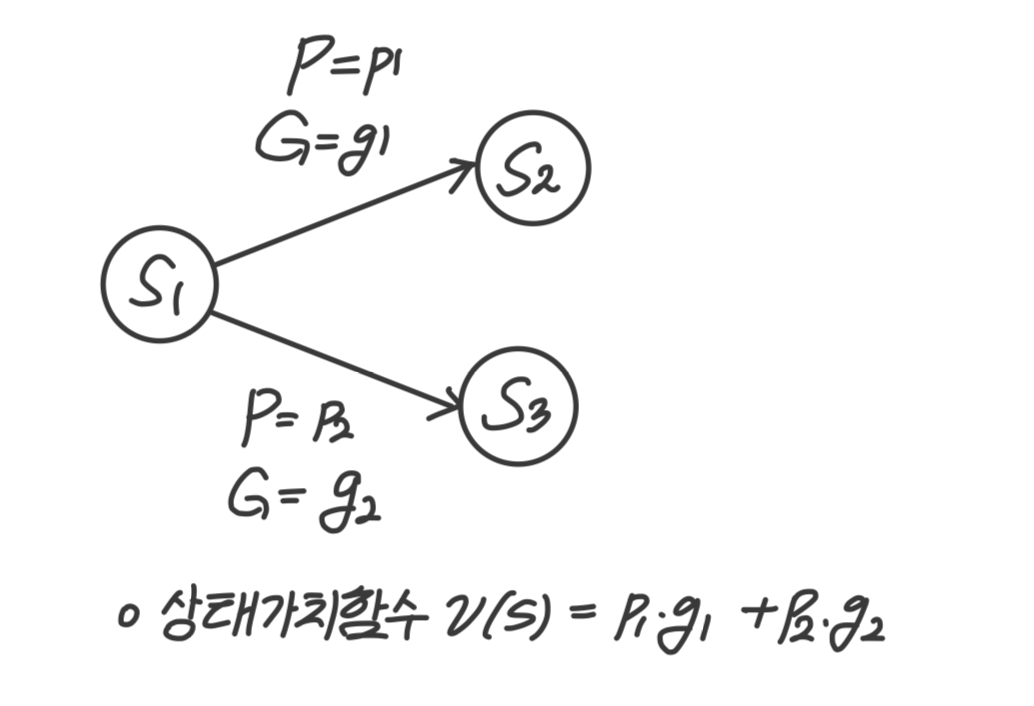 상태 가 에서 가질 수 있는 상태가 2개()이고 각각으로 갈 확률이 이며, 각 상태변화에 따른 보상이 일 때 보상함수는 아래와 같다.
상태 가 에서 가질 수 있는 상태가 2개()이고 각각으로 갈 확률이 이며, 각 상태변화에 따른 보상이 일 때 보상함수는 아래와 같다.
: 확률을 곱해 기댓값 형태로 나타냈다. 상태 의 보상은 t+1에서 계산된다. -
감가율 (, 할인율)
MRP의 목적은 가치를 계산하는 것인데, 이 가치는 보상함수를 사용해 하나의 에피소드 혹은 전체 환경의 가치를 한꺼번에 모두 계산한다. 그리고 그 가치는 현재가치로 환산되어야 한다. 여러 번의 타임스텝 후에 얻게 되는 현재가치를 환산하는데, 여기에 감가율을 사용하는 것이다. 이자율을 생각해보면 된다.
감가율이 0이면 미래의 보상을 전혀 고려하지 않는 것이고, 감가율이 1이면 현재와 미래의 가치를 동일하게 보는 것이다.
여기에서 반환값(: return)이라는 개념이 등장한다.
반환값은 타임스텝 t에서 계산한 누적 보상의 합계이다. 반환값은 주로 전체 환경이 아닌 에피소드 단위로 계산하는데, 에피소드의 효율성이나 가치를 반환값을 통해 평가하며, 이 반환값을 극대화할 수 있도록 환경을 설계하는 것이 MRP의 목적중 하나다.
- 반환값
여기에서 특이한 점은 상태전이확률을 고려하지 않는다는 점이다. 반환값은 하나의 선택된 경로(에피소드)에 대한 전체적인 보상을 계산하는 방법이기 때문이다. (= 이미 경로가 결정된 상태에서 계산하는 게 반환값. 확률은 필요 없다.)
- 반환값 계산 예시
감가율을 0.5로 설정. 3타임스텝에 목적지에 도달하는 에피소드는 모두 3가지. 각 노드마다 보상이 정해져 있고, 이 보상값에 타임스텝이 진행됨에 따라 감가율을 계속 곱해줌.
-
상태가치함수(v : State Value Function)
반환값(G)으로 에피소드 하나에 대한 가치를 측정할 수 있었다면, 상태가치함수는 환경 전체에 대한 가치를 측정한다. 상태전이확률을 같이 고려한다는 점이 반환값과 다른 점이다.측정 대상 특징 감가율 r 상태 전이 확률 P 반환값 G 에피소드 합계 사용 미사용 상태 가치 함수 v 전체 환경 기댓값 사용 사용
MRP 상태 가치 함수

1. 타임스텝 t가 상태 s에 있을 때의 반환값의 기댓값으로 정의한다.
- 아래 그림과 식을 보면 이해하기 쉽다.
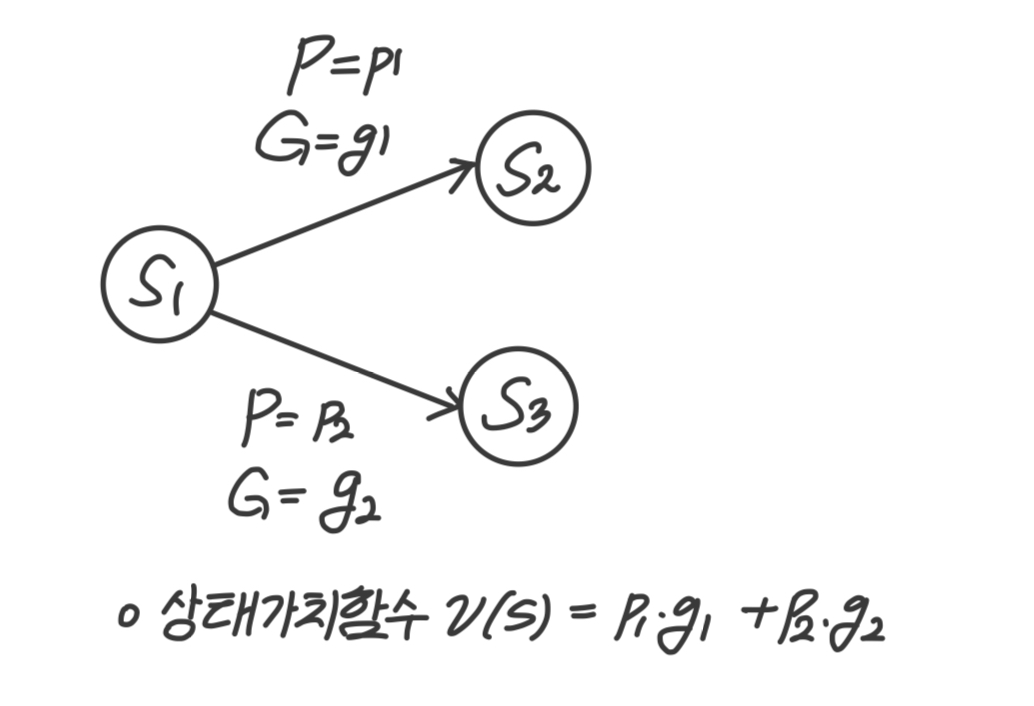
- 반환값을 구하는 식을 그대로 집어넣는다.
- 다음 타임스텝의 반환값을 감가율()로 묶는다.
- 이것을 다음 타임스텝의 반환값으로 대치한다.
- 마지막 수식은 반환값 대신에 상태가치함수를 집어넣은 것이다. 반환값을 상태가치 함수로 대체할 수 있는 이유는 반환값에 대한 기대값을 구하면 상태 가치함수를 구하는 것과 같기 때문이다.
- 상수를 기댓값에서 빼줌
- 기댓값을 수열의 합과 다음 상태에서의 상태 가치 함수로 나타낸 것. 이것을 벨만 방정식이라 부른다.
벨만 방정식(Bellman Equation)
벨만 방정식(Bellman Equation)는 MRP의 상태 가치 함수를 일반화하여 프로그래밍이 가능한 형태로 만든 것이다. 강화학습에서는 프로그래밍으로 가치를 구하기 위해 이 방정식을 많이 사용한다.
- 벨만 방정식 : 현재 상태의 가치함수와 다음 상태의 가치함수 사이의 관계
벨만 방정식은 일반적으로 기댓값을 시그마 기호를 사용한 수열의 합으로 표현하며 현재상태와 다음상태의 관계로 나타낸다.
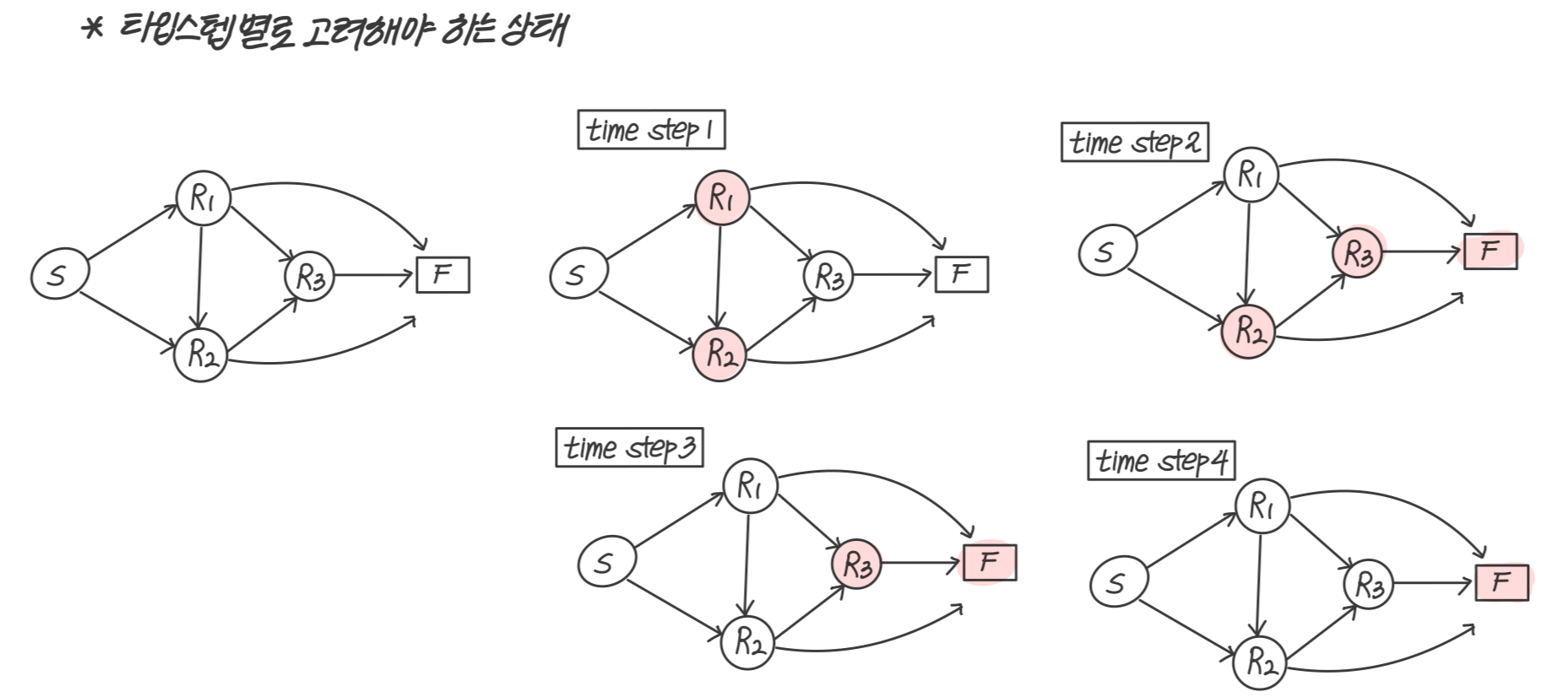
위와 같은 상황에서 벨만 방정식을 그대로 적용해 직접 가치를 계산하는 것은 쉬운 일이 아니다. 벨만 방정식을 사용하는 이유는 프로그래밍을 통해 문제를 해결하기 위함이다.
간단한 네트워크로 구성된 라우팅 문제의 경우 순차적으로 반환값을 구해 상태가치함수를 계산할 수 있다.
