
1. 거리함수(metric, distance function)
metric이라고도 하는 거리함수에 대해 알아보자.
1.1 거리함수의 조건
거리함수는 아래와 같은 조건을 만족하는 함수를 의미한다.
2. Similarity and Dissimilarity
거리함수는 말그대로 어떤 점과 점 사이의 거리를 나타내며, 거리함수 종류에 따라 유사도(similarity) 또는 상이성(Dissimilarity)으로 표현된다.
1. Similarity Measure
Similarity measure는 두 data object가 얼마나 유사한지를 나타내며, 수가 커질수록 서로 유사하다고 얘기한다.
2. Dissimilarity Measure
Dissimilarity measure은 두 data obejct들이 얼마나 서로 다른지를 나타내며, 수가 클수록 상이하다고 얘기한다.
Proximity
Proximity(근접성)은 Similarity와 Dissimilarity를 포괄하는 말이다.
3. Norm
Norm은 벡터의 크기, 또는 길이를 측정하는 방법을 일반화한 것을 의미한다. 두 벡터 사이의 거리를 측정하는 방법을 의미하기도 한다.
4. Euclidean Distance (L2 Norm) 유클리드 거리
오늘 알아볼 거리함수는 가장 기본적인 거리함수들이다.
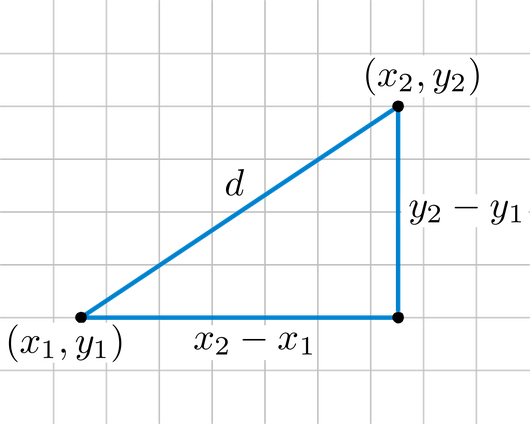
Euclidean Distance 또는 Euclidean Norm(노름)이라고도 한다.
또, L1 Distance, L1 Norm 이라고도 한다.
4.1 수식
수식은 아래와 같다.
- 인 p와 q(n차원 벡터)에 대하여 두 점 사이의 거리를 구하고자 할 때 사용하는 수식
- 벡터의 요의 차이의 제곱의 합에 제곱근을 씌워준 것과 같음
4.2 특징
- 중학교때부터 배운 피타고라스 정리는 2차원 유클리드 공간에서 거리를 구한 것이다.
- regularization과 regression에서 사용된다. 자세한 내용은 아래에서 더 설명.
4.3 장점
- 거리에 기반한 유사도 측정 방식이기 때문에 두 데이터 사이의 스케일차이가 크지 않은 경우에 사용하기에 좋음
(cf. 각도 기반 유사도 측정은 스케일 차이가 큰 경우에 사용하기에 좋음) - Outlier에 신경을 써야 하는 경우에 사용하기에 좋다.
4.4 단점
- (Euclidean Distance를 Loss function으로 이용할 경우) 만약에 실제값과 예측값 사이의 오차를 구할 때 Euclidean Distance를 이용한다면 다음과 같은 식이 성립하는데, , 이는 오차의 제곱을 더하는 것이기 때문에 Manhattan Distance(L1 Loss)보다 Outlier에 더 큰 영향을 받는다. 즉, L2 Loss가 L1 Loss에 비해 Outlier에 대하여 더 민감하다고 할 수 있다.
- 동일한 시점에서 관찰된 두 시계열 데이터 사이의 거리만을 측정할 수 있음 (문서 유사도를 측정할 때에도 유클리드 거리는 문서의 길이에 영향을 받기 때문에 자주 사용하지 않음)
5. Manhattan Distance (L1 norm) 맨해튼 거리
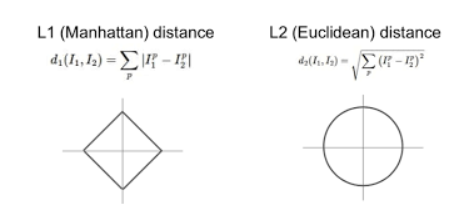
- L1 Distance라고도 부름 (cf)유클리드 거리는 L2 Distance임)
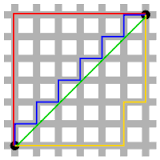
- 밑의 그림에서 초록색 선이 최단 거리인 유클리드 거리를 의미하고, 파란색 선, 빨간색 선, 노란색 선은 맨해튼 거리를 의미함, 이때 파란색 선, 빨간색 선, 노란색 선의 길이는 모두 동일한 것이 특징
- 회색을 도로, 흰색 블록을 건물이라고 생각한다면 건물을 뚫고 지날 수 없기 때문에 맨해튼 거리를 이용하여 거리를 측정
5.1 수식
n차원 공간에 위치한 두 점 p, q 사이의 거리는 각 좌표의 차이의 절댓값을 모두 합한 것과 같다.
5.2 Euclidean Distance & Manhattan Distance
p는 norm의 차수를 의미하며(p=1은 L1 norm, p=2는 L2 norm) n은 대상 벡터의 요소 수, 즉 벡터의 차원을 의미한다.
5.3 장점
- 유클리드 거리와의 비교: 유클리드 거리를 이용하게 되면 고차원이 될 수록 대부분의 점들이 유사한 거리를 가지게 되기 때문에 고차원에서는 유용하지 않다. 이런 경우에 맨해튼 거리가 유클리드 거리보다 유용하다고 할 수 있다. 또한 데이터의 차원이 다른 경우에도 맨해튼 거리가 유클리드 거리보다 낫다. 그리고 norm의 지수가 클 수록 큰 값의 원소에 거리가 치우치고 작은 값이 무시된다.
- 유클리드 거리와 달리 제곱을 하지 않기 때문에 차원의 영향력을 줄일 수 있음 ⇒ 고차원 벡터 사이의 거리를 구할 때 Euclidean Distance보다 일반적으로 나음
5.4 특성
- 맨 왼쪽 아래의 점에서 맨 오른쪽 위의 점으로 이동할 때 각 좌표축의 방향으로만 이동할 경우에 사용되는 거리이다.
6. Minkowski Distance 민코프스키
6.1 개념
-
L1(맨해튼), L2(유클리드) norm 을 일반화한 함수이다.
→ p=1일 때 맨해튼 거리와 같고, p=2일 때 유클리드 거리와 같음
→ p→무한으로 가면 체비셰프 거리
6.2 수식
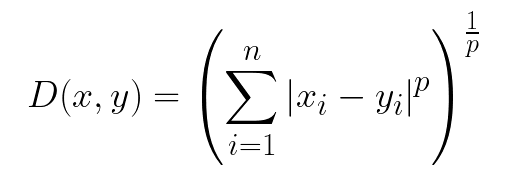
6.3 특성
- user case에 적합한 m을 찾아 거리 측정을 할 수 있다는 점에서 유연성을 가짐
- 민코프스키 시공간(Minkowski spacetime)
- 사람이 인지하는 현실세계인 3차원 공간에, 1차원 시간을 더하여 4번째 차원으로 이루어진 공간
- 시공간이지만, 시간(t)에 속도(c)를 주어서 시간을 거리 함수처럼 다룸
7. Chebyshev Distance (L-infinity norm) 체비셰프 거리
p 를 무한대로 보내는 경우 체비셰프 거리라고 한다.
7.1 수식
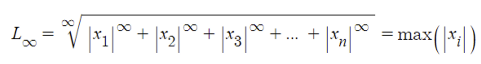
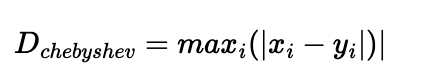
7.2 정의 및 특성
- 벡터 성분의 절댓값 중 가장 큰 값으로 거리를 구한다.
8. Regularization
Norm이라는 개념을 통해 예측값과 실제값의 차이인 Loss(cost)를 계산할 수 있다.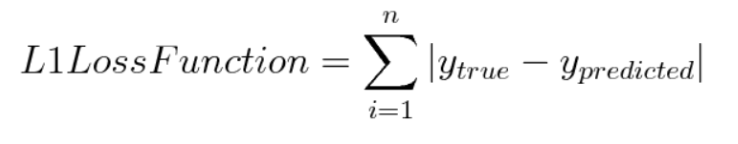
8.1 Regularization
모델 학습을 할때 과적합을 방지하기 위해 cost function 에 규제항을 넣어준다. 특정 변수 또는 Weight가 과도하기 커지지 않도록 하는 역할이 Regularization이다.
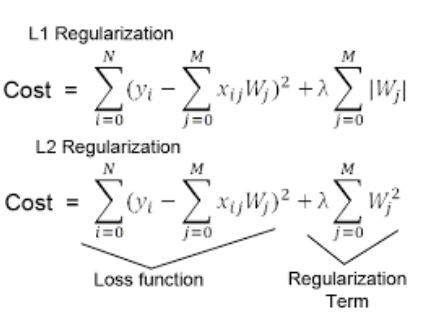
Regularization Term으로 맨해튼 거리와 유클리디안 거리를 사용한다.
8.2 L1 Regularization
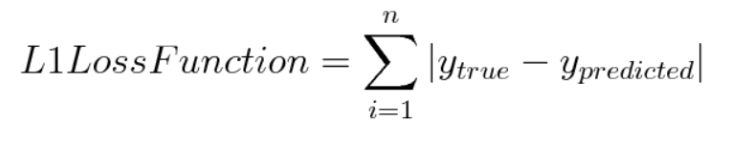
Lasso(라쏘) model : L1 Regularizaition을 사용하는 선형 회귀 모델을 말함
8.3 L2 Regularization
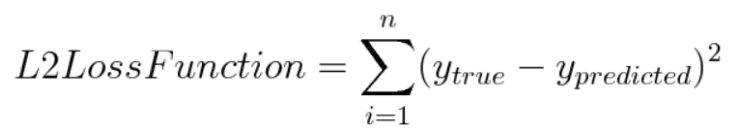
Ridge(릿지) model : L2 Regularizaition을 사용하는 선형 회귀 모델을 말함
8.4 변수 선택에서 라쏘와 릿지
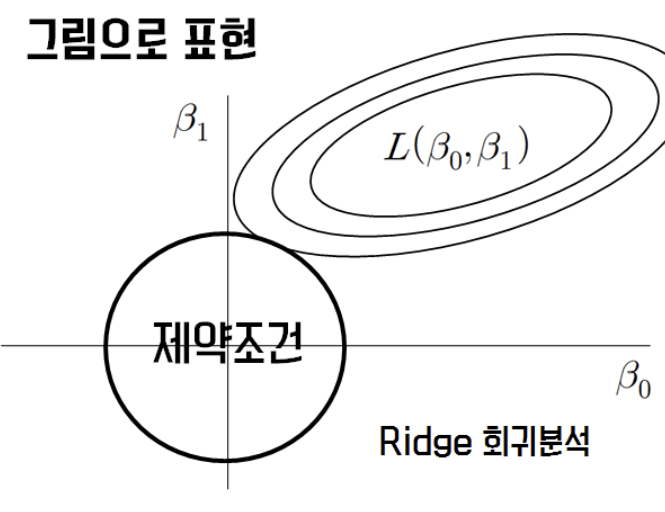
Regularization 를 사용하는 선형 회귀 모델에서 중요하게 봐야할 것이 이 함수의 모양이다.
맨해튼은 사각형, 유클리디안은 원처럼 생긴 걸 볼 수 있다. 이 모양 때문에 L1(라쏘)의 경우가 L2(릿지) 변수선택에서 더 많이 쓰인다.
라쏘와 릿지는 계수추정치를 제한(constraints or regularizes)하여 계수 추정치가 0에 가까워 지게 함으로, p개 독립변수를 모두 포함하는 모형을 만들 수 있다.
그러나 릿지의 가중치들은 0에 가까워질 뿐 0이 되지는 않는다. 특성이 많은데 그중 일부분만 중요하다면 라쏘가, 특성의 중요도가 전체적으로 비슷하다면 릿지가 좀 더 괜찮은 모델을 찾아줄 것이다.
지금 배가 고파서.. 이부분은 나중에 좀 더 채워보겠음
