마할라노비스 거리(Mahalanobis Distance)의 직관적 이해와 수식적 이해

soyyeong·2023년 7월 23일

distance 데이터사이언스

데이터사이언스

목록 보기

2/2

📖 마할라노비스 거리의 정의

위키피디아에서는 마할라노비스 거리를 다음과 같이 정의하고 있다.

D의 평균에서 P가 얼마의 표준 편차로부터 떨어져 있는지를 측정하는 것을 다차원적으로 일반화한 것을 의미함

다시 말하면,
'평균과 거리가 표준편차의 몇 배인지를 나타내는 값'으로 확률분포상의 거리를 얘기한다.

무슨 말인지 모르겠으니 조금 더 살펴보자.

➰ 직관적인 이해

출처 : https://darkpgmr.tistory.com/41

위 블로그에서 직관적인 이해를 쉽게 설명하고 있다.
교통량을 체크한다고 해보자.

하루에 차가 평균 20대, 표준편차는 3대가 지나간다고 할 때
--> 하루에 평균적으로 20대가 지나가고, 들쑥날쑥한 정도가 평균적으로 3대라는 정도로 이해해볼 수 있다. 따라서 하루에 17~23대가 지나가는 경우가 일반적이라고 생각할 수 있다.

근데 어느날 26대가 지나갔다. 평균보다 6대나 더 많이 지나갔고, 일반적으로 17~23대가 지나가기 때문에 이 날은 특히 교통량이 많았다고 볼 수 있다.

마할라노비스 거리는 그 값이 얼마나 일어나기 어려운(힘든) 값인지를 수치화한 방법이다.

26대가 지나간 경우는 흔치 않다는 것을 어떻게 수치화할 수 있을까?
마할라노비스 거리로 아래처럼 구할 수 있다.

Mahalnobis distance = (26-20)/3 = 2

즉, 26대가 지나간 것은 표준적인 편차의 2배 정도의 오차가 있는 값이라는 것이다.

이때 주의해야 할 것은 서로 다른 두 점 사이의 거리가 아니라 한 점(관측치)과 분포 사이의 거리를 계산했다는 점이다.

🔎 수식적인 이해를 위한 배경

바로 수식으로 들어가기 전에 위 내용을 그림으로 다시 확인해보자.

위처럼 파란 점들로 이루어진 분포가 있다고 할때,
노란색 점끼리의 거리와 빨간색 점끼리의 거리는 유클리디안 거리로는 같다.
그러나 분포상에서 상대적인 거리는 노란색 점끼리의 거리가 빨간색 점끼리의 거리보다 더 멀다고 할 수 있다.

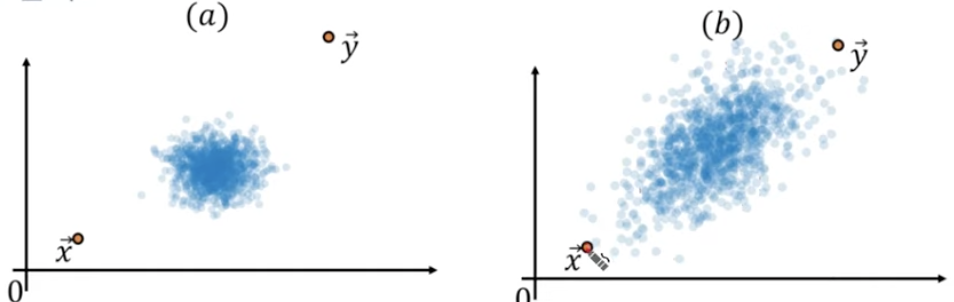
주변에 있는 다른 데이터 분포를 고려한다면, (a)에서의 두 점의 거리가 (b)에서의 두 점의 거리보다 더 멀다고 표현하는 게 더 맞지 않을까?

이것을 수식적으로 표현하고자 하는 것이 마할라노비스 거리다.

어떻게 수식으로 표현할 수 있을까?

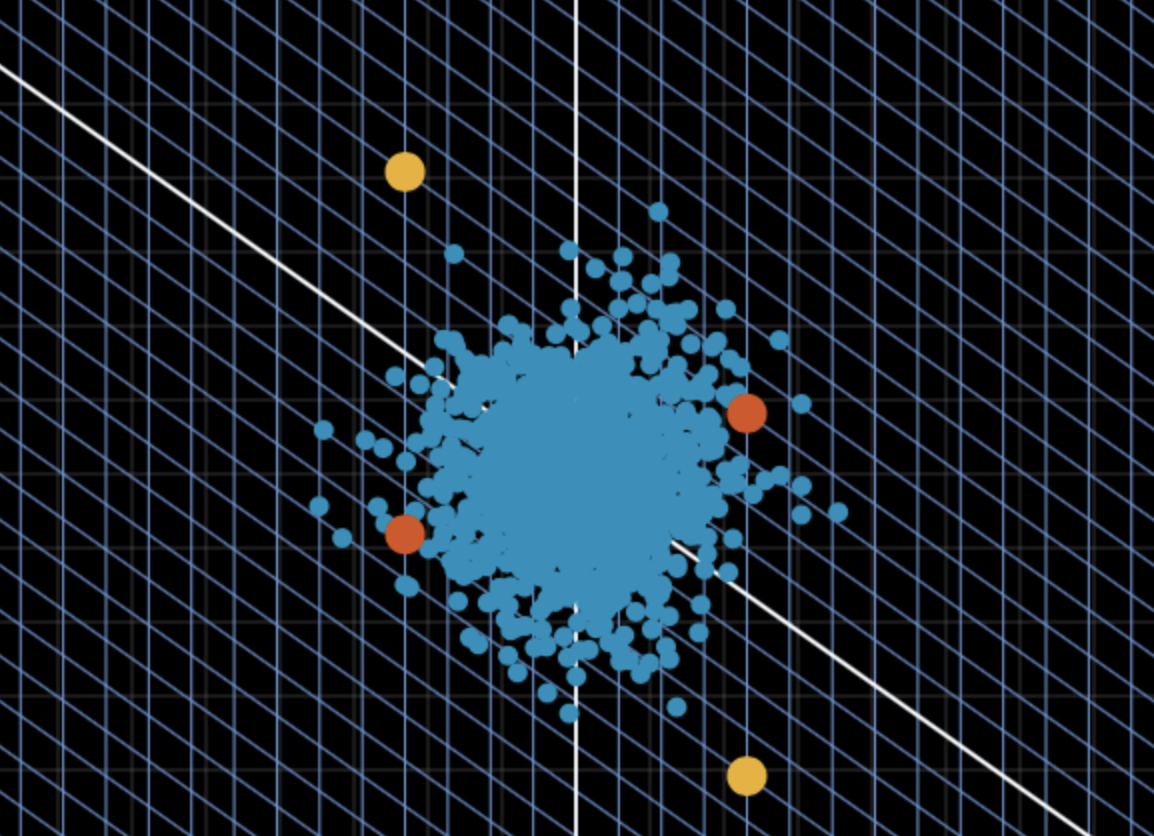
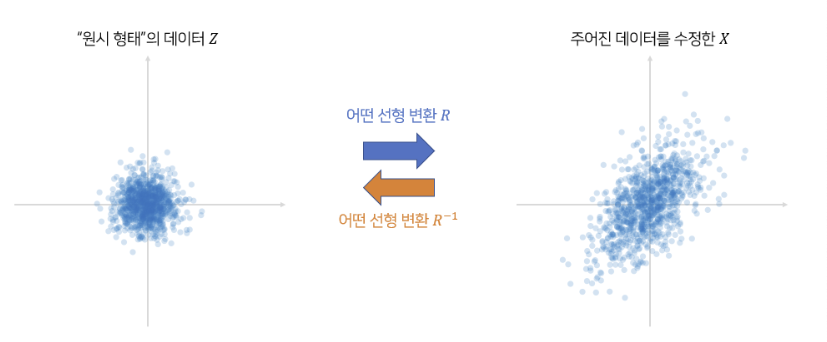
위처럼 파란색 점(데이터)들을 정규화 시키는 선형변환을 통해 축을 변형시키고, 그 위에서 노란점, 빨간점을 표현하면 노란색끼리의 거리가 더 멀다는 것을 시각적으로 확인할 수 있다.

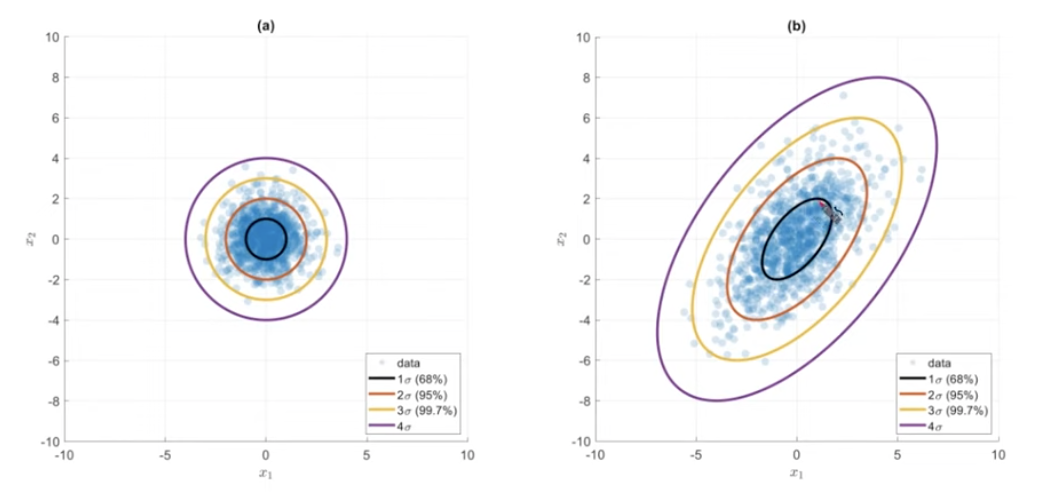
이런 상대적인 거리를 표현하기 위해, 표준편차를 사용해 정규화(선형변환)를 한 다음에 유클리디안 거리를 구하면 된다.

🔎 마할라노비스 거리 공식

마할라노비스 거리 식은 아래와 같다.

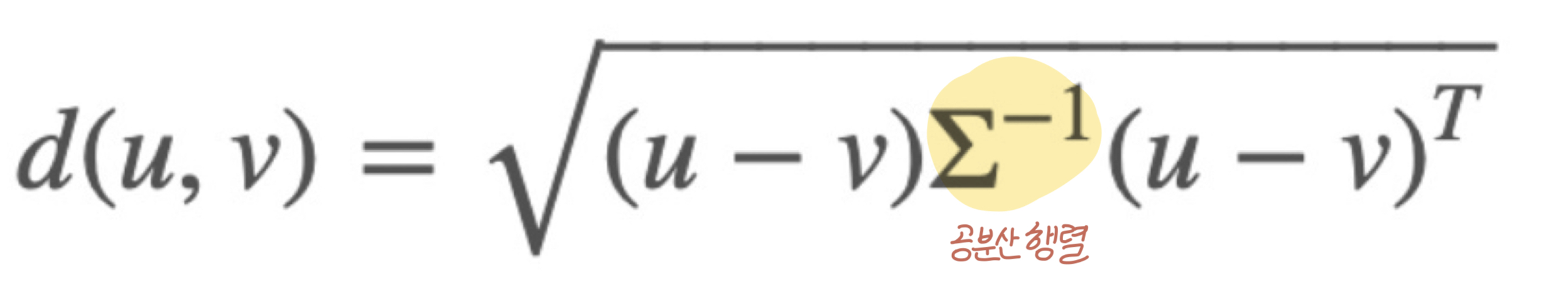
u와 v는 두 점을 말하는 거고, 식 중간에 공분산 행렬의 역행렬이 하나 들어갔다.

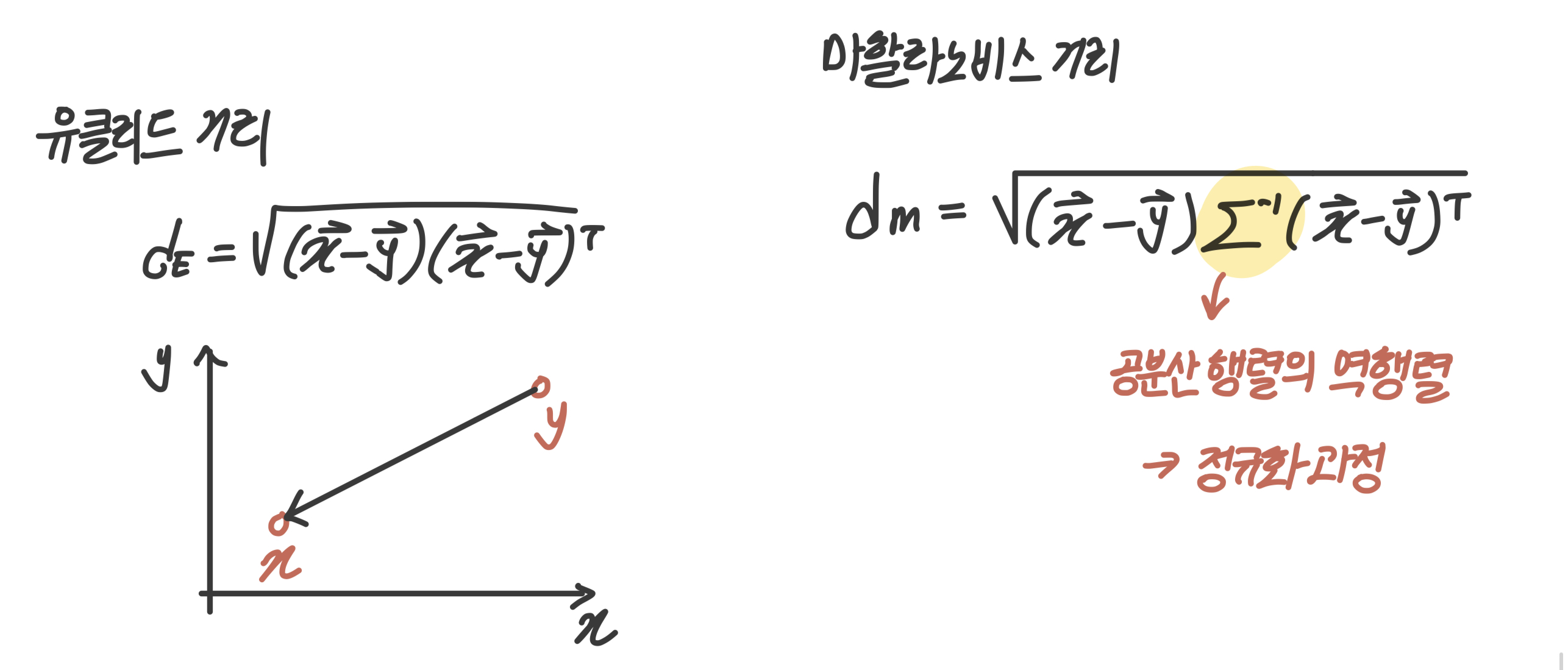
식이 어려워보이는데 사실 유클리드 거리 식의 중간에 '공분산 행렬의 역행렬' 하나만 추가된 거다.

공분산 행렬의 역행렬이 데이터를 정규화하는 과정이라 생각하면 된다.

공분산 행렬의 이해

이것을 더 이해하기 위해 공분산 행렬을 이해해보자.
아래는 공분산 행렬이 도출되는 과정이다.

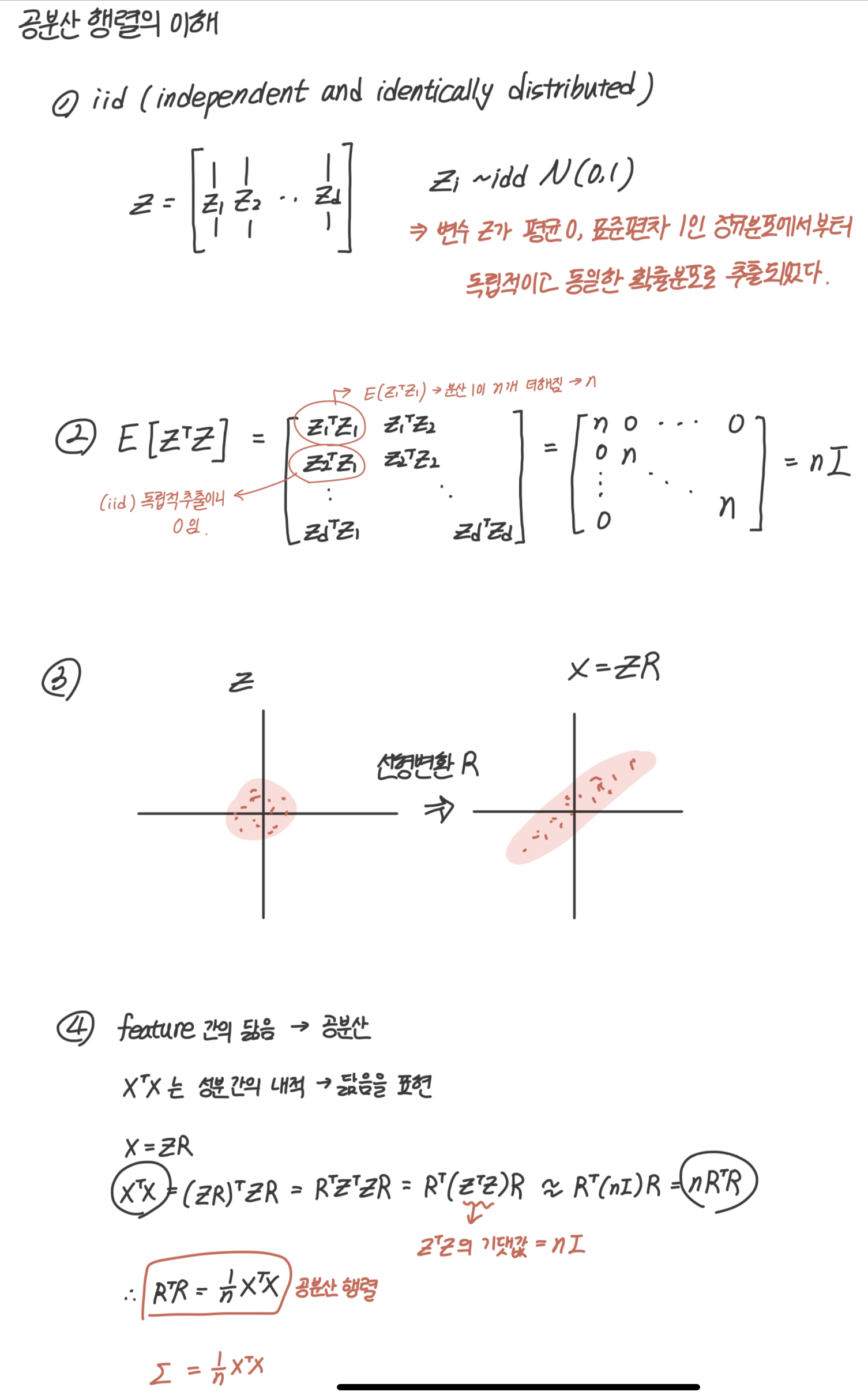
1) iid(independent and identically distributed)

Z라는 데이터가 평균이 0이고, 표준편차가 1인 정규분포에서부터 독립적이고, 동일한 확률분포로 추출되었다고 해보자. 이를 iid라고 한다.

2) $Z^TZ$ 의 기댓값

$Z^TZ$ 의 기댓값을 계산하면 nI가 나온다.
대각성분은 분산이 1이 n개가 있으니 n,
대각성분 외에는 독립적으로 추출되었으니 0이 된다.

3) Z를 선형변환하여 X = ZR로 바꾸자

정규화되어 있는 Z 데이터를 선형변환시켜서 새로운 $X=ZR$ 이라는 데이터를 만들어보자.

4) 공분산 행렬 도출

$X^TX$ 는 성분간의 내적을 의미하는데, 내적은 닮음을 표현할 수 있고, 이 feature간의 닮음은 곧 공분산이 된다.

이를 통해 아래와 같은 식으로 공분산 행렬을 도출할 수 있다.

$X^TX = (ZR)^TZR = R^TZ^TZR = R^T(Z^TZ)R \approx R^T(nI)R = nR^TR$

이를 정리하면, 아래처럼된다.

$R^TR \approx \frac{1}{n}X^TX$

중간에 ' $\approx$ ' 가 들어간 건, 실제데이터에서는 기댓값과 정확히 같은 값이 나오지 않기 때문

위 식이 의미하는 것은, 정규화된 데이터 Z를 X로 변환하기 위한 선형변환 R에 대한 $R^TR$ 과 거의 같다. 공분산 행렬을 보통 $\sum$ 으로 표현하며 정리하면 아래와 같다.

$\sum = \frac{1}{n}X^TX$

*(표본 공분산은 n-1로 나눈다.)

마할라노비스 거리 공식 도출

$d_Z = \sqrt{ZZ^T} = \sqrt{(XR^{-1})(XR^{-1})^T} = \sqrt{X\sum^{-1}X^T} \Rightarrow \sqrt{(x-y)\sum^{-1}(x-y)^T}$

최종적으로 우리는 X를 정규화된 형태인 Z로 선형변환시킨 후, 거리를 구하고 싶은 거기때문에 위처럼 계산해주면 마할라노비스 식을 얻을 수 있다.

*(위 수식적인 이해는 '공돌이의 수학정리노트'를 참고하였습니다!)

💻 소스코드와 예제

소스코드

직접 구현

def mahalanobis(x=None, data=None, cov=None):
    """Compute the Mahalanobis Distance between each row of x and the data  
    x    : vector or matrix of data with, say, p columns.
    data : ndarray of the distribution from which Mahalanobis distance of each observation of x is to be computed.
    cov  : covariance matrix (p x p) of the distribution. If None, will be computed from data.
    """
    x_minus_mu = x - np.mean(data)
    if not cov:
        cov = np.cov(data.values.T)
    inv_covmat = sp.linalg.inv(cov)
    left_term = np.dot(x_minus_mu, inv_covmat)
    mahal = np.dot(left_term, x_minus_mu.T)
    return mahal.diagonal()

df_x = df[['carat', 'depth', 'price']].head(500)
df_x['mahala'] = mahalanobis(x=df_x, data=df[['carat', 'depth', 'price']])
df_x.head()

출처 : https://www.machinelearningplus.com/statistics/mahalanobis-distance/

라이브러리 사용
scipy.spatial.distance 라이브러리 내에서cdist()함수에서 입력 매개 변수에 mahalanobis를 지정하여 사용가능.

import numpy as np
from scipy.spatial.distance import cdist

x = np.array([[[1,2,3],
               [3,4,5],
               [5,6,7]],
              [[5,6,7],
               [7,8,9],
               [9,0,1]]])

i,j,k = x.shape

xx = x.reshape(i,j*k).T


y = np.array([[[8,7,6],
               [6,5,4],
               [4,3,2]],
              [[4,3,2],
               [2,1,0],
               [0,1,2]]])


yy = y.reshape(i,j*k).T

results =  cdist(xx,yy,'mahalanobis')
results = np.diag(results)
print (results)

import numpy as np
from scipy.spatial.distance import cdist

x = np.array([[[1,2,3],
               [3,4,5],
               [5,6,7]],
              [[5,6,7],
               [7,8,9],
               [9,0,1]]])

i,j,k = x.shape

xx = x.reshape(i,j*k).T


y = np.array([[[8,7,6],
               [6,5,4],
               [4,3,2]],
              [[4,3,2],
               [2,1,0],
               [0,1,2]]])


yy = y.reshape(i,j*k).T

results =  cdist(xx,yy,'mahalanobis')
results = np.diag(results)
print (results)