고등학교때 수학학원 선생님께서 게임이론 관련된 책을 읽고 재밌었다고 말씀하셨던 적이 있다. 그게 뭔지 잘 모르겠지만 그렇게 재밌다니 나도 나중에 읽어봐야지.. 하고 있다가 경영과학 시간에 게임이론을 배우게 됐다! 우리네 인생과 비슷하면서도.. 또 어떤 점에서는 다른 게 흥미롭다.
내가 좋아하는 조승연, 장동선 두 분이 나와서 치킨게임, 죄수의 딜레마 등을 재밌게 설명하는 영상이 나왔다. 이걸 보고 게임이론을 공부하면 더 재밌다 :)
🔗 유투브 영상 : 🕹️뇌과학게임으로 보는 큰 성과를 이뤄내는 사람들의 특징
게임이론이란?
게임이론이란, 두 명 이상의 참가자가 이해관계가 상충하는 상황에서 각자 자신의 이익을 최대화하기 위해 어떤 전략을 택해야 할지 연구하는 학문이다.
제갈량과 조조의 전쟁게임
조조는 적벽대전 패배 후 퇴각하는 중이다. 넓고 대피하기 쉽지만 오래걸리는 '대로', 그리고 좁고 이동이 불편하지만 빠른 '소로' 중 어디로 대피할지 고민중이다. 제갈량도 둘 중 한 곳에만 복병을 배치할 수 있고, 어디에 배치할지 고민중이다. 이 결과는 내가 선택하는 전략뿐만 아니라 상대방에 선택하는 전략에 따라 결정된다.
조조는 소로에서 연기가 나자, 제갈량이 소로에 사람이 있는척 연기를 피우고 사실은 대로에 복병을 배치했을 거라 생각하고 소로로 퇴각하게 된다.
그러나 제갈량은 그 상황까지 예측하고 사실은 소로에 복병을 배치한다.
게임의 종류
게임은 3가지의 기준으로 나눌 수 있다.
1. 2인 게임 vs 다인 게임
- 2인 게임(two-person game) : 참가자가 2명
- 다인 게임(n-person game) : 참가자가 3명 이상
2. 영화게임 vs 비영화게임
- 영화게임(zero-sum game) : 참가자의 게임 결과의 합이 0이 됨 (누가 100을 잃으면, 누군 100을 잃음) ex. 노사협상
- 비영화게임(non zero-sum game) : 게임 결과의 합이 0이 되지 않는 게임 ex. 광고전략
3. 협력게임 vs 비협력게임
- 협력게임(cooperative game) : 게임 시작 전, 참가자들이 완전히 구속력있는 협약을 맺고 진행하는 게임
- 비협력게임(non-cooperative game) : 협약없이 서로 자신의 이익을 극대화하기 위해 최선의 전략을 찾으려는 게임
2인 영화게임 (two-person zero-sum game)
2인 영화게임에는 (1) 경기자 1의 전략, (2) 경기자 2의 전략, (3) 이득표(성과표, payoff table)가 필요하다. 이걸 보통 테이블로 표현하는데 이 테이블 안의 숫자는 경기자 1이 얻는 payoff이다. 'zero-sum'게임이기 때문에 경기자2는 경기자1이 받는 payoff에 - 를 취한 값이 된다.
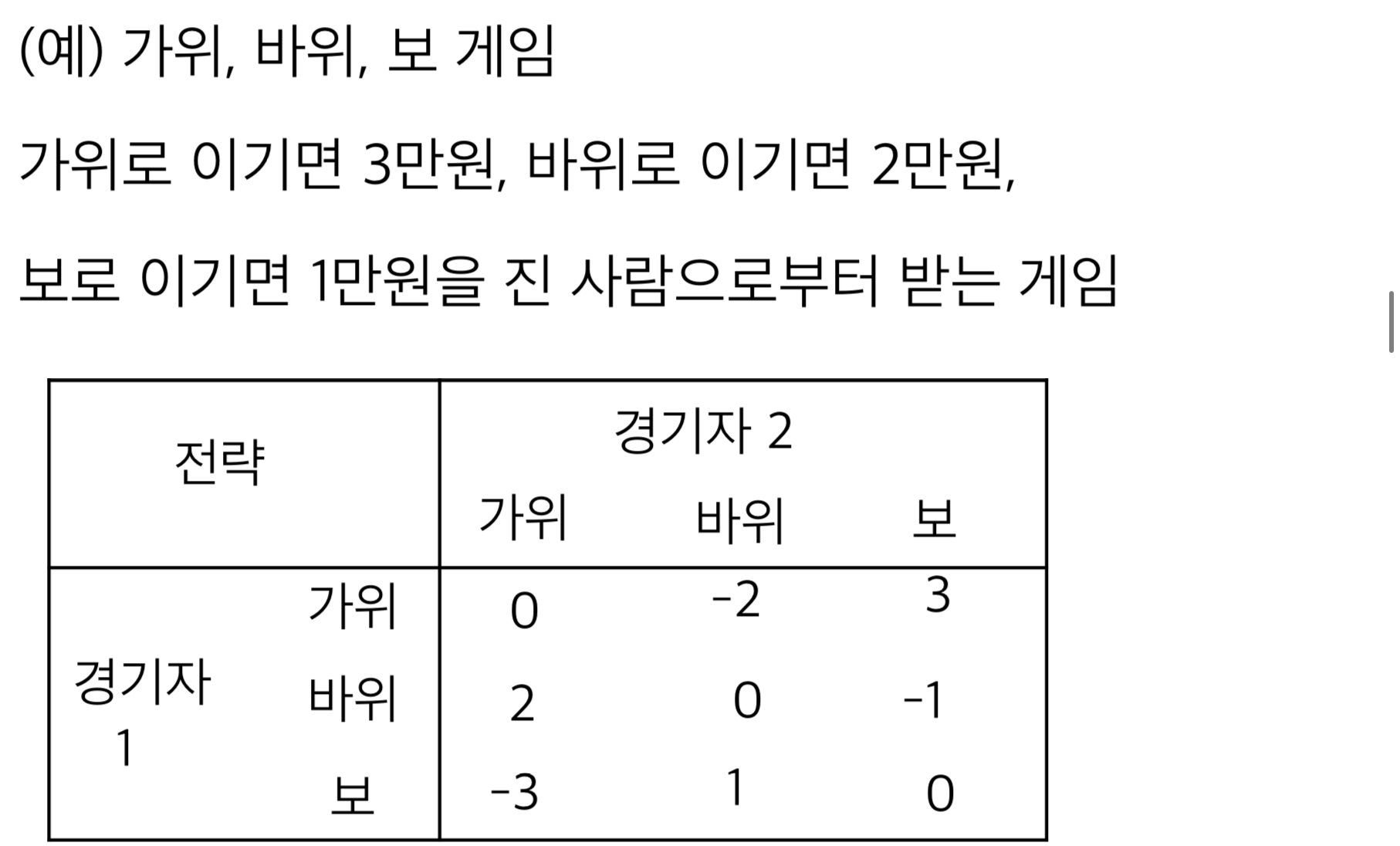
2인 영화게임에는 아래와 같은 가정이 필요하다.
1. 두 경기자는 모두 이성적이다.
2. 두 경기자는 각각 상대방에 대한 동정심 없이 오직 자기의 이익만을 추구하여 전략을 선택한다.
이 가정으로, 자신의 몫을 지키기 위해 자기 방어적인 Maximin 전략을 사용하게 된다. Maximize min 이라고 보면 되는데, 내가 가질 수 있는 이익 중 최소값(하한)이 가장 커질 수 있게 Maximize 하는 전략이다.
열등전략 vs 우위전략
열등전략(dominated strategy)과 우위전략(dominant strategy)은 각각 Strictly, Weakly로 나뉜다.
-
Strictly 열등전략(Strictly Dominated Strategy)
상대방이 어떤 전략을 선택하든 상관없이 전략 A가 전략 B보다 불리하면, "전략 A는 전략 B에 대해 Strictly 열등전략이다" 라고 표현한다.상대전략 i -
Weakly 열등전략(Weakly Dominated Strategy)
최소 하나의 상대전략에서는 불리하고, 나머지에서는 불리하거나 동일한 이득을 주면 , "전략 A는 전략 B에 대해 Weakly 열등전략이다" 라고 표현한다.( 상대전략 i ) & ( 상대전략 i )
우위전략(dominant strategy) 도 마찬가지로 Strictly, Weakly로 나뉜다.
이성적인 경기자는 (Strictly or Weakly) 열등전략을 사용하지 않는다.
예제) 정치인 선거유세일정 문제
선거에서 두 정치인 1과 2가 대결하는 중이다. 앞으로의 유세기간은 2일이고, 두 정치인 모두 남은 2일 동안 도시 갑과 을에서 유세할 것을 계획중이다. 두 후보는 상대방의 일정은 알지 못 한다. 최선의 유세전략을 세우려고 한다.
각 정치인은 세 가지 전략을 가지고 있다.
-
전략 1 : 각 도시에서 하루씩 유세
-
전략 2 : 도시
갑에서 2일 유세 -
전략 2 : 도시
을에서 2일 유세-
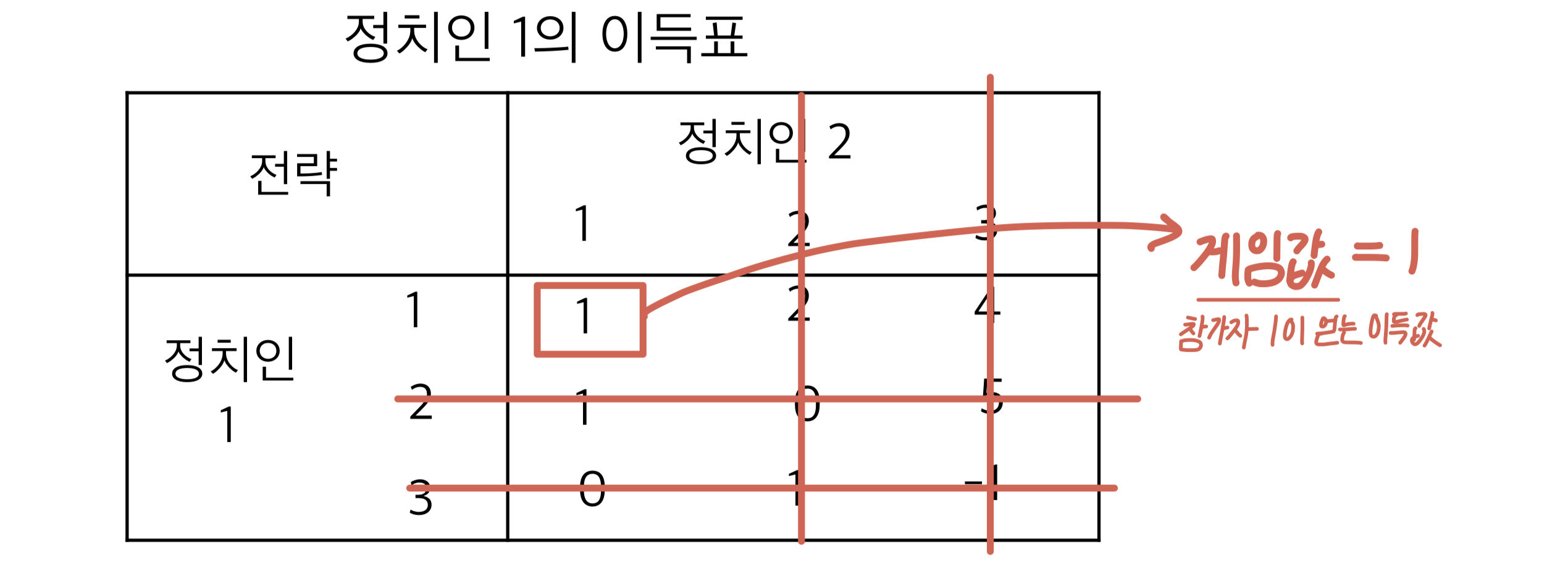
이 전략을 세웠을 때 이득표는 아래와 같다.
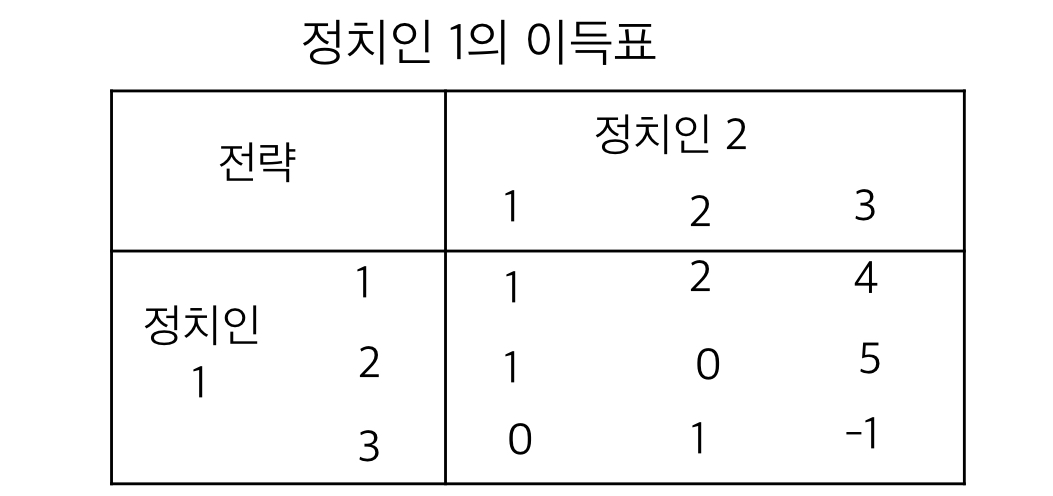
-
이 상황에서 정치인 2의 경우에는 열등전략이 존재하지 않는다. 하나의 전략이 확실히 불리한 게 없다. 그러나 정치인 1의 경우, 전략 3을 사용했을때 전략 1, 2를 사용했을 때보다 Strictly 열등하다. 따라서 정치인1은 전략 3을 사용하지 않는다. 그리고 정치인 2도 정치인1이 전략3을 안 쓸 거라는 걸 알고 있다.

-
이 이득표는 정치인1의 입장이기 때문에, 정치인2의 입장에서는 숫자가 클수록 안 좋은 거다. 정치인 2가 전략 3을 쓰면 전략1,2에 대해 Strictly 열등전략이 되기 때문에 정치인2는 전략 3을 쓰지 않을 것이다.
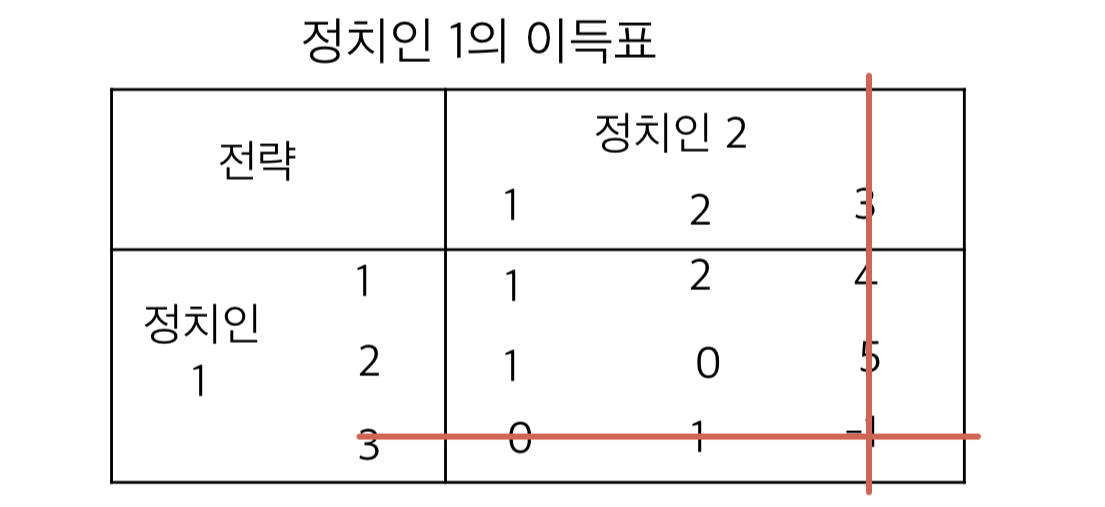
-
이번에 정치인 1 입장에서 전략 2는 전략 1에 대해 Weakly 열등전략이다. 따라서 전략 2를 버린다.
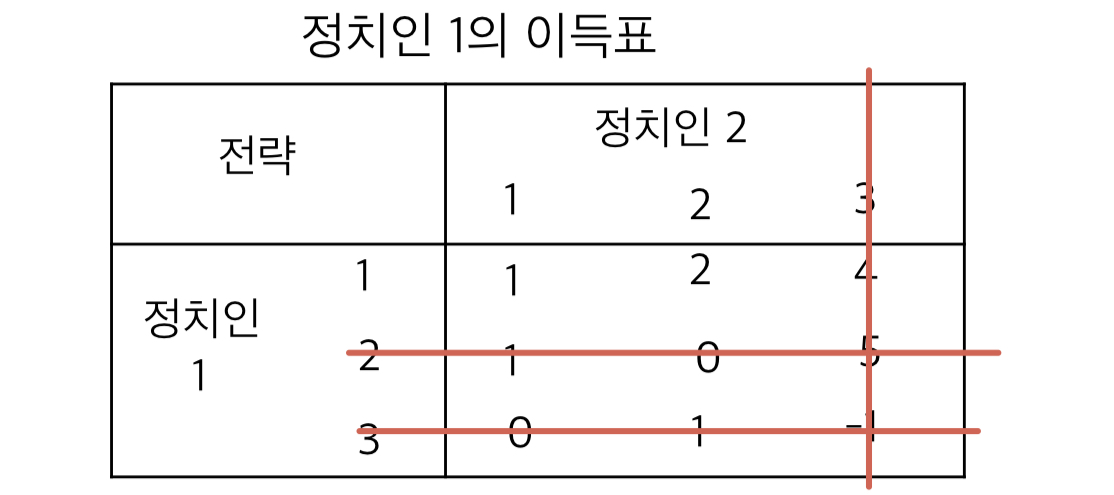
-
정치인 2 입장에서는 전략 2가 전략 1에 대해 Strictly 열등전략이 된다.따라서 전략 2를 버린다.
-
결국에 두 정치인은 모두 전략 1을 선택하게 된다. 정치인 1은 1의 이득을, 정치인 2는 -1의 이득을 얻게 된다.
-
그리고 여기에서 정치인 1이 얻는 이득을
게임값이라고 한다. 게임값이 0이 아니므로 정치인 1에게 유리한, 불공정한 게임이다.
-
최대최소기준, 최소최대기준 적용
위에서 푼 문제를 좀 더 쉽게 풀 수 있다. 최대최소(Maxi min), 최소최대(Mini max)를 적용하면 된다.
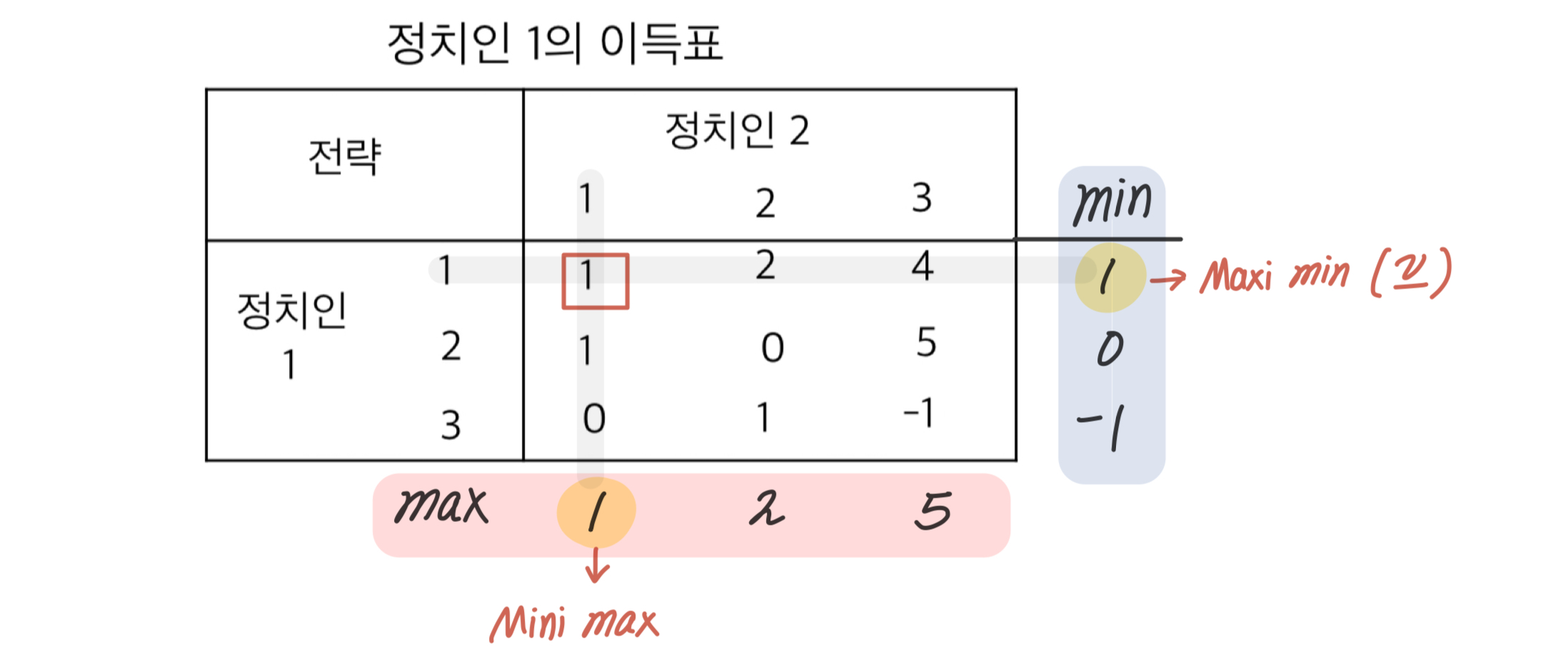
정치인 1 입장에서 먼저 보자. 파란색 부분의 min을 보면된다. 전략1을 썼을 때 가능한 이익은 1,2,4이고 그 중 정치인 2가 이성적이라면 정치인1의 이익을 가장 작게 만드는 1이 선택되게 할 것이다. 마찬가지로 정치인 1이 전략 2를 썼을 때 1, 0, 5 이익 중 0, 전략 3을 썼을 때 0, 1, -1 이익 중 -1의 이익을 얻게 될 것이다.
이 세 개의 전략을 썼을 때 각 1, 0, -1의 이익을 얻게 될 것이고 정치인 1은 그 중에서 이익이 가장 큰 1을 선택하게 된다.
그래서 이 과정을 Maxi min 이라고 하는데, 하한을 가장 크게 만드는 전략을 선택하는 것이다. 그때의 값을 lower value라고 부르고 으로 표현한다.
이제 정치인 2 입장에서 보자. 정치인 2가 전략 1을 선택했을 때, 정치인 1은 최대의 이익을 얻으려고 할 것이므로 그때 발생하는 이익은 1이다. 전략 2를 선택했을 때는 2, 전략 3을 선택했을 때는 5의 이익이 있다. 그러나 이 이익은 정치인 1의 입장에서의 이익이기 때문에 정치인 2는 이 중(1, 2, 5)에서 가장 작은 이익을 선택할 것이고 결국 1이 선택된다.
그래서 이 과정을 Mini max라고 하며, 상한을 가장 작게 만드는 전략을 선택하는 것이다. 그리고 이때의 값을 upper value라고 부르고 으로 표현한다.
전략 중 꼭 하나만 실행하는 '순수전략' 에서는 균형해가 존재하는 경우와 균형해가 존재하지 않는 경우로 나뉜다.
(1) 순수전략에 의해 균형해가 존재하는 경우
위와 같은 경우, 정치인 1과 2 모두 전략 1을 취하는 게 서로에게 이성적인 결과이다. 위 예시 처럼 이 성립하는 경우에 이 점을 '안장점(saddle point)'라고 한다. 안장점이 존재하는 경우, 어떤 경기자든 전략을 바꾸면 더 안 좋은 상황이 되기 때문에 현 전략을 고수하려고 한다. 이러한 해를 '균형해(안정해)' 라고 한다.
(2) 순수전략에 의해 균형해가 존재하지 않는 경우
하나의 전략만을 선택하는 '순수전략'의 경우에는 균형해가 존재하지 않을 수 있다.
아래 예시를 보자. 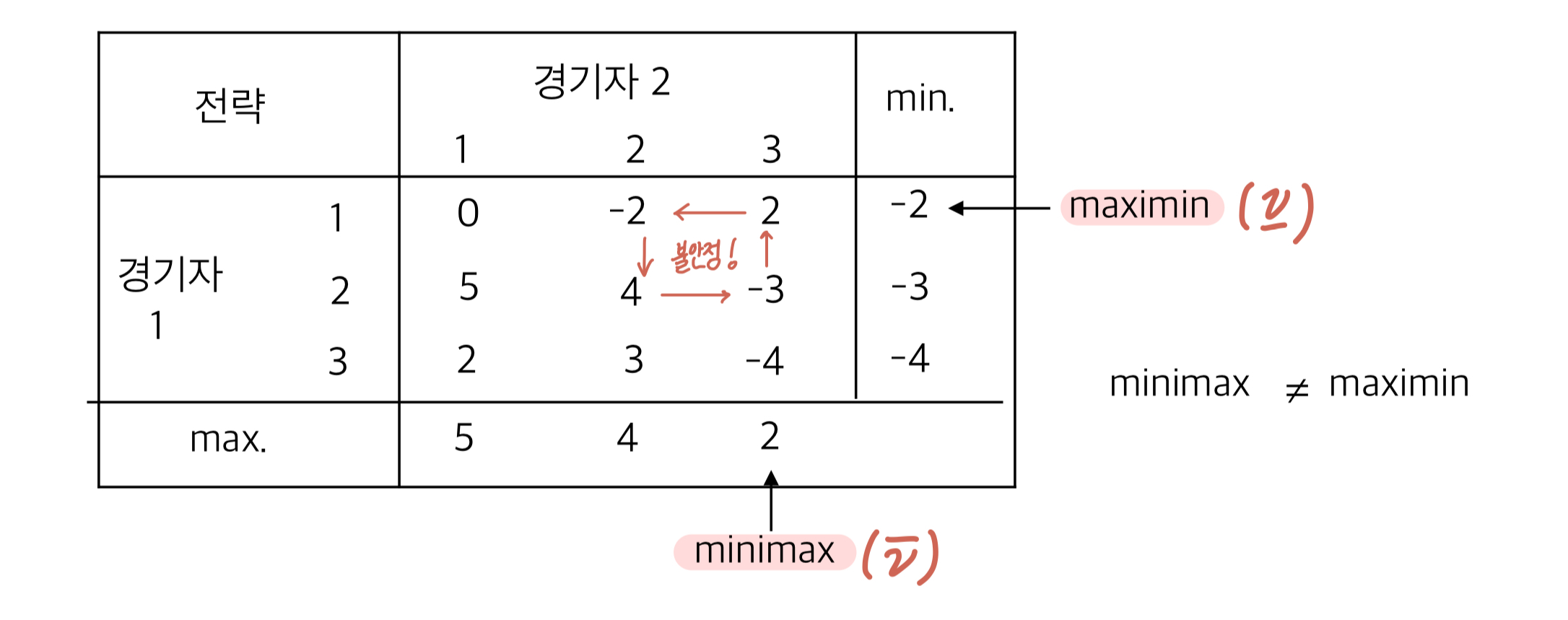
으로 안장점이 존재하지 않는다. 경기자 2는 경기자 1이 전략 1을 선택하면 전략 2를 사용하는 게 유리해서 전략 2로 변경할 것이다. 그러면 또, 경기자 1은 전략 2가 유리해서 전략 2로 변경한다. 그럼 경기자 2는 전략 3을 선택할 거고, 그럼 경기자 1은 전략 1을 선택할 것이다. 이렇게 과정이 순환될 수 있다. 이런 상황을 불안정한 해(unstable solution) 이라고 한다.
한 경기자의 전략이 예측가능하면 상대방이 이러한 정보를 이용해 자기 입장을 좋게 하려고 한다. 따라서 상대방의 전략을 예측하지 못하도록 '혼합전략' 을 사용한다. 혼합전략은 전략을 딱 하나만 선택하는 게 아니라 여러 전략을 확률적으로 선택하는 것이다.
혼합전략 -> 균형해가 존재
혼합전략이란?
전략집합에 확률분포를 할당하고 확률분포에 따라 전략을 무작위한 방법으로 선택하는 것이다. 
최소최대정리(Minimax Theorem)
혼합전략이 허용될 경우 최소최대기준에 의해 최적이 되는 한 쌍의 혼합전략은 (게임값) 을 갖는 균형해를 갖는다. 따라서 어느 쪽도 일방적으로 전략을 바꿈으로써 자신의 입장을 좋게 할 수 없다.
최적 혼합전략 구하기
최적 혼합전략을 구하는 방법은 두 가지 방법이 있다.
(1) 선형계획법에 의한 해법 -> 어떠한 2인 영화게임에도 적용 가능
(2) 그래프에 의한 해법 -> 어느 한 경기자의 전략이 두개 뿐일 경우 적용 가능
여기에선 (2) 그래프에 의한 해법을 알아보자.
그래프 해법으로 최적 혼합전략 구하기
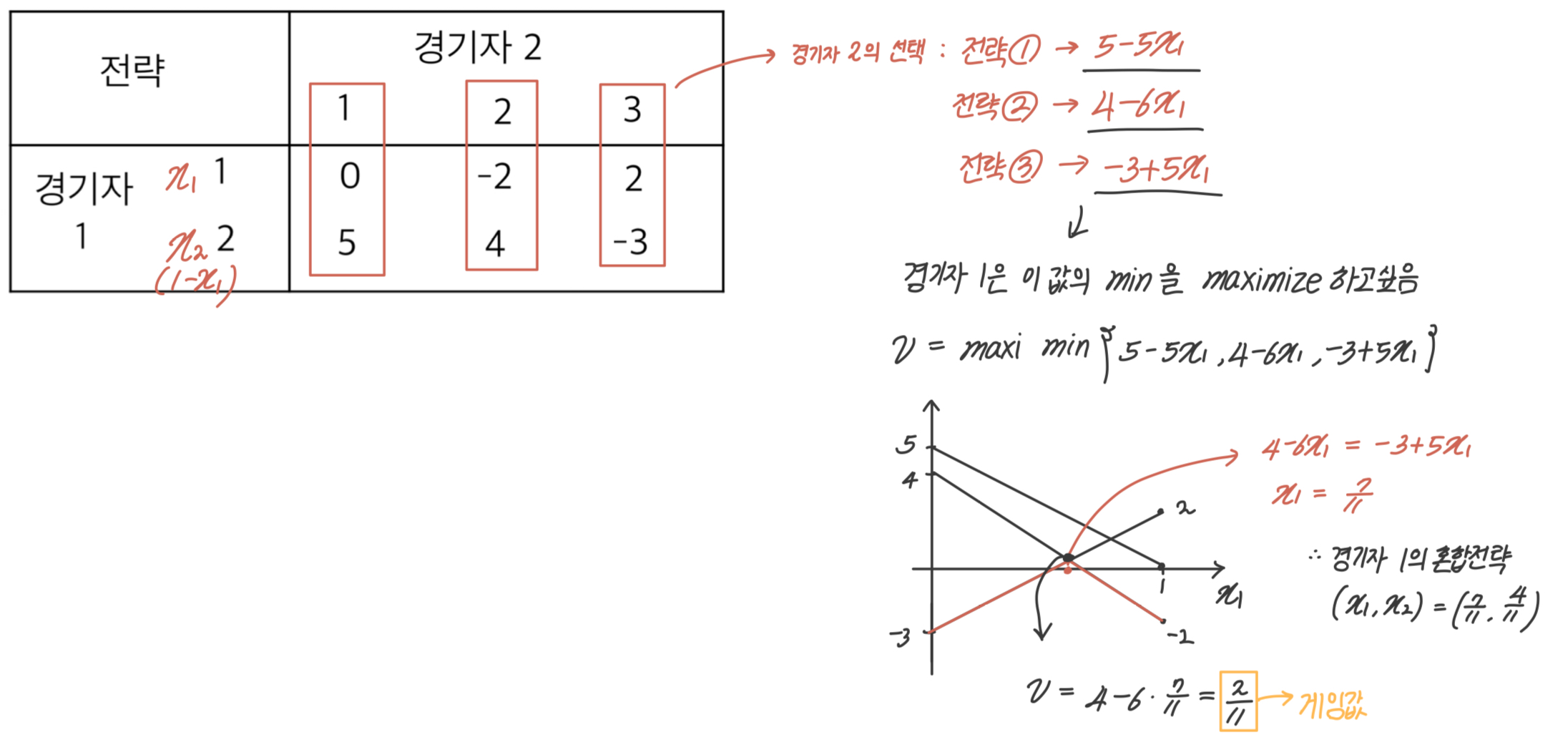
아래처럼 순수전략에서는 균형해가 존재하지 않는 문제를 혼합전략에서 그래프 해법으로 풀어보자.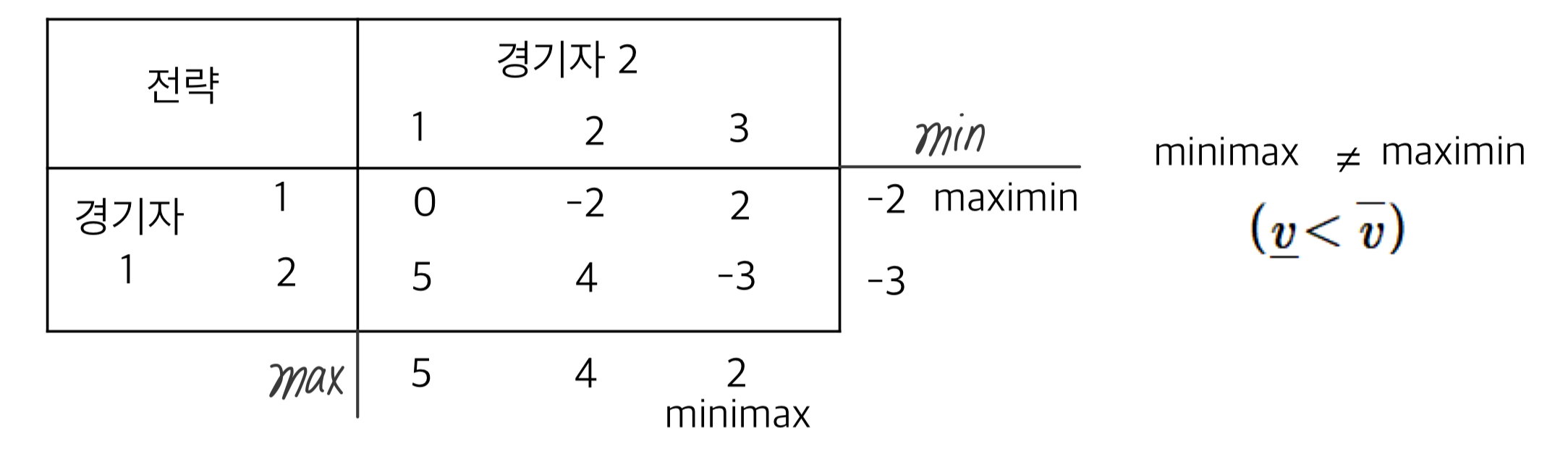
- 경기자 1이 전략 1을 선택할 확률 :
- 경기자 1이 전략 2을 선택할 확률 :
경기자 2의 선택이 전략 1이냐, 2이냐, 3이냐에 따라 경기자 1이 얻는 이익은 , , 이다. 경기자 1은 이 값의 최솟값을 maximize 하고 싶다. 따라서 아래처럼 그래프를 그려 최소값이 max가 되는 지점을 찾으면 된다.
- 경기자 1의 혼합전략 :
- 게임값 :
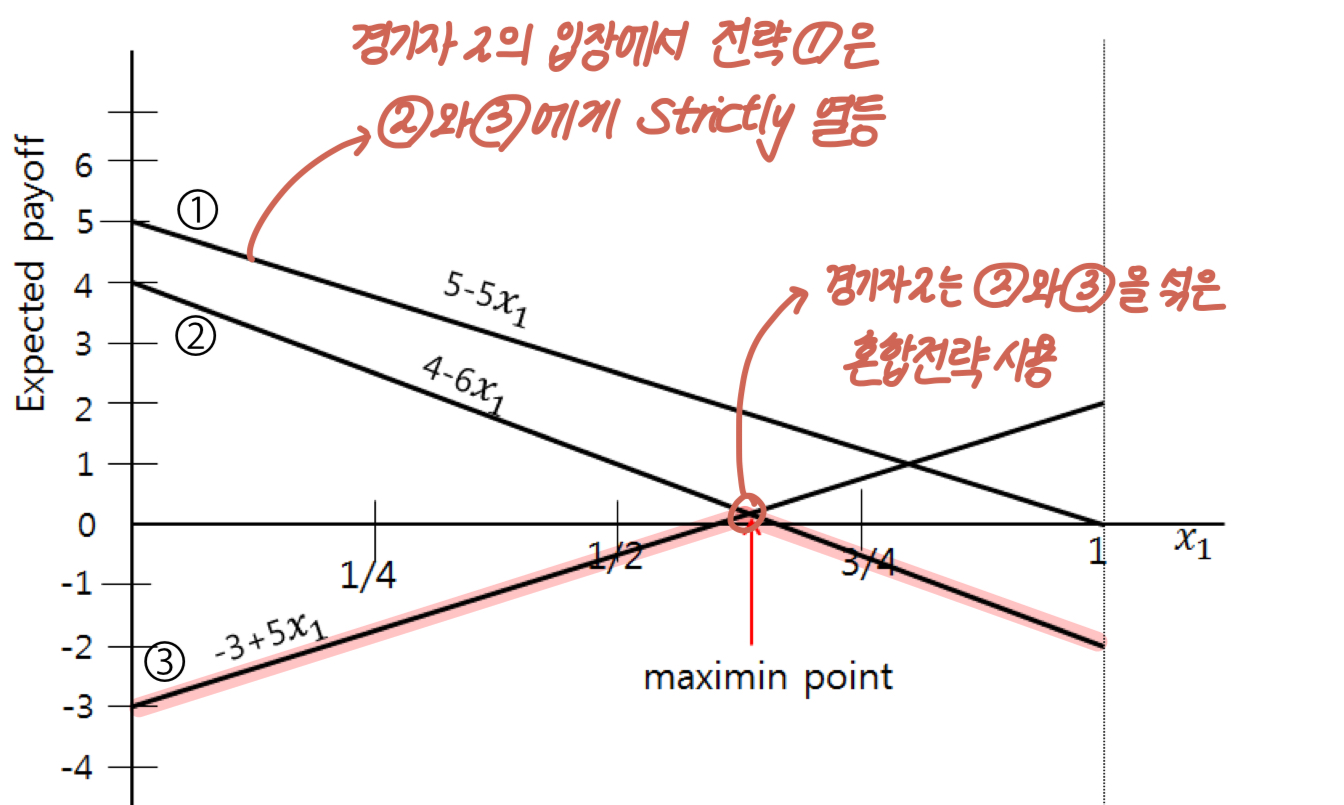
아래는 경기자 2의 입장에서 본 것이다.
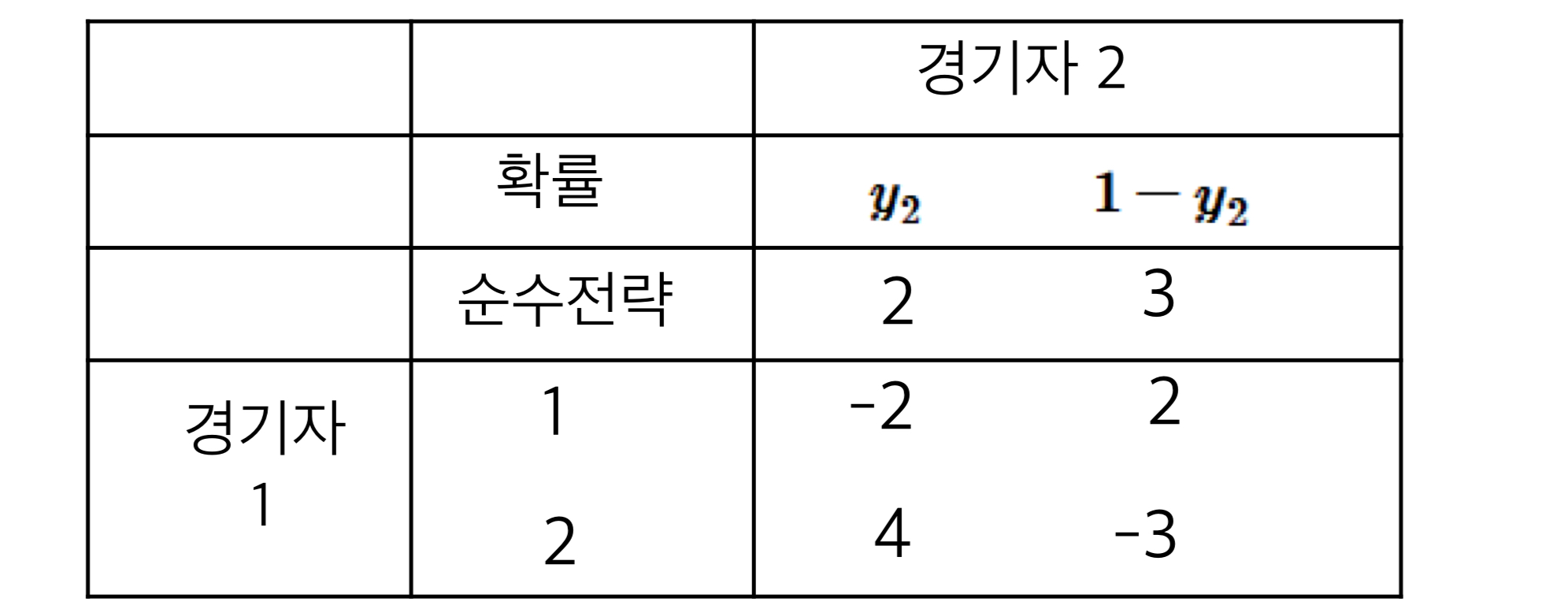
이번엔 경기자 2의 입장에서 아래 문제를 풀어 보자. 전략 1은 위에서 본 것처럼 열등전략이므로 사용하지 않는다. 따라서 전략 2와 3만 고려한다.
풀이는 위와 비슷하다. 이렇게 게임값을 구하면 위에서 구한 값과 똑같은 걸 알 수 있다.
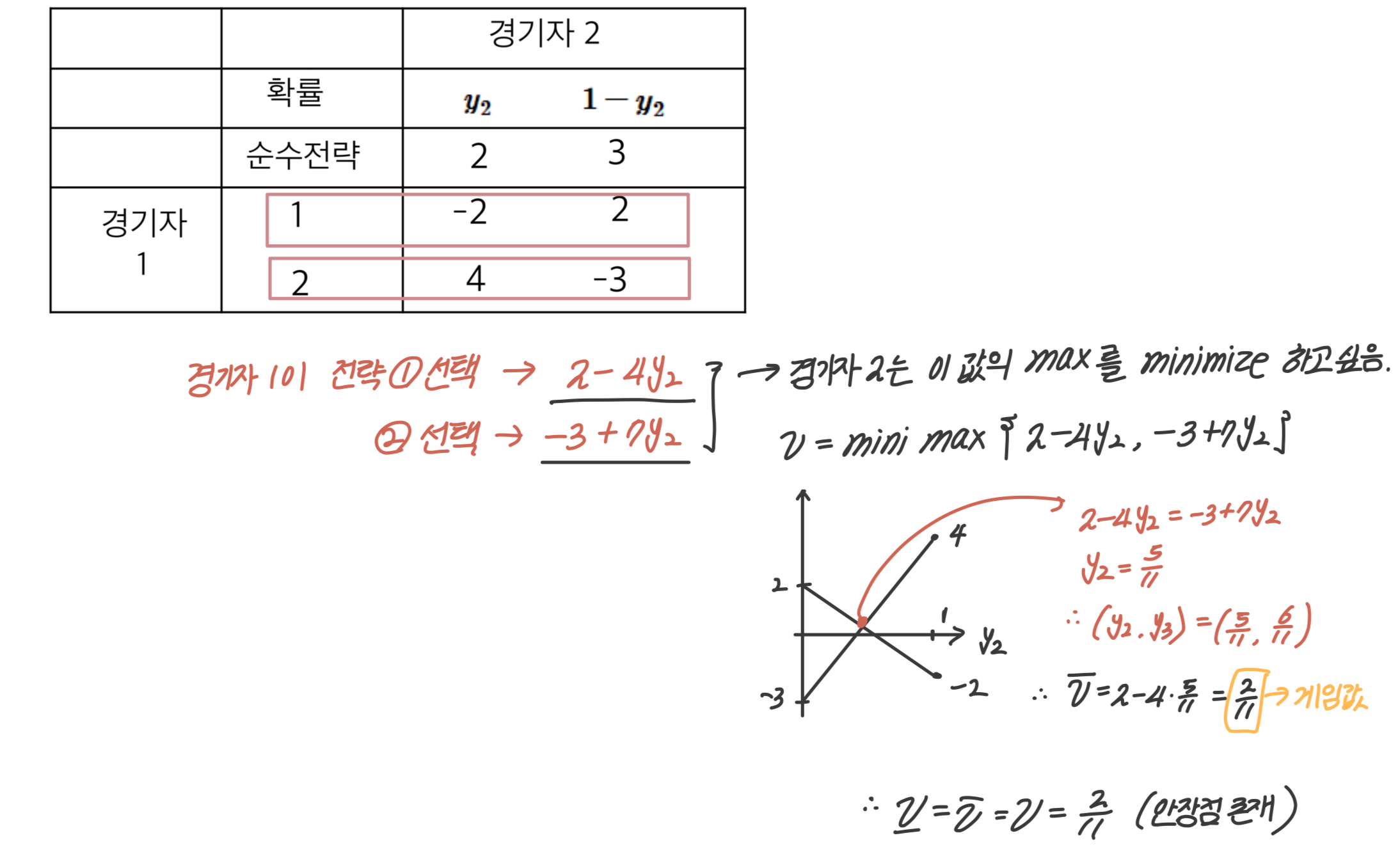
이렇게 2인 영화게임에서의 순수전략일 때의 문제와 혼합전략으로 푸는 방법을 알아봤다.
다음에는 2인 영화게임의 혼합전략을 선형계획법으로 구하는 방법과 왜 게임이 쌍대문제인지, 2인 비영화 게임(non zero-sum game), 내쉬균형점, 치킨게임을 알아보자!
