메타 휴리스틱

• [메타 휴리스틱] 1. 타부서치
• [메타 휴리스틱] 2. 시뮬레이티드 어닐링
• [메타 휴리스틱] 3. 유전자 알고리즘

다음 글은 경영과학에서 배우는 내용을 정리함.

0️⃣ 유전자 알고리즘이란?

유전자 알고리즘도 시뮬레이티드 어닐링처럼 자연의 현상을 모방한 방법이다. 시뮬레이티드 어닐링은 물리적 담금질이라는 자연 현상에서 아이디어를 가져왔고, 유전자 알고리즘은 다윈의 진화이론에 영향을 받았다.

진화이론
생물 종 중에서 환경에 적응해서 개별적인 변이가 일어난 개체가 다음 세대에 더 생존(적자생존, survival of fittest)한다. 자손은 부모로부터 염색체(chromosomes)을 물려 받고, 이 염색체 내의 유전자(genes)는 자손의 특성을 결정한다.
부모로부터 좋은 형질을 물려받은 자손이 더 많이 생존하고, 부모가 되었을 때 다음 세대에게 그 형질을 물려준다.
또한, 가끔이지만 돌연변이(mutation)가 발생하여 형질이 랜덤하게 변화된다. 대부분의 돌연변이는 단점이 많지만, 일부는 개선된 형질을 가지고 있다.

이런 생물학적 아이디어를 최적화 문제에 적용한 것이 유전자 알고리즘이다.
타부서치, 시뮬레이티드 어닐링은 초기해 하나를 사용해 변화시켰다면,
유전자 알고리즘은 여러 해인 해 집단, 여기에서는 '모집단(population)'을 사용한다.

✔️ 용어 정리

• 모집단(population) : 실행 가능한 해들의 집합
• 세대(generation) : 유전자 알고리즘의 반복횟수
• 개체 : 해
• 적합도(fitness) : 목적함수 값
• 부모 : 랜덤하게 선택된 개체 중, 2개를 선택해 한 쌍의 부모로 만듦
• 번식 : 부모의 형질이 랜덤하게 섞인 2개의 자식 태어남
• 유산(miscarriage) : 번식과 돌연변이로 실행 불가능한 해가 발생한 경우. -> 번식에 실패하면 성공할 때까지 번식해야 한다.
• 염색체 : 해를 표현하기 위한 것으로, 유전자 알고리즘은 보통 문자열로 표현.
• 부호화 : 해를 염색체로 표현하는 것을 의미함
• 동일교배 : 두 자식이 생성되는 방식이 같은 경우를 의미함

✔️ 유전자 알고리즘 과정

a. 초기화 : 모집단을 랜덤하게 만든다. 적합도를 평가한다.

b. 반복단계 : 부모는 적합도가 큰 개체를 랜덤하게 선택;
		    부모의 형질이 랜덤하게 섞인 2개의 자식이 태어남;
            유산되면 번식이 성공할 때까지 번식해야 함.
            새로운 세대의 모집단의 크기를 유지하기 위해 이전 모집단 + 자식집단에서 적합도 좋은 일부를 선택하여 다음세대의 모집단을 구한다.
            
c. 종료단계 : 정해진 반복횟수나 CPU시간이 지나면 종료;
			또는 정해진 반복횟수동안 목적함수의 개선이 없는 경우;
            정해진 반복횟수동안 실행가능한 영역으로 이동할 수 없는 경우;
            => 지금까지 찾은 해 중 가장 좋은 해 출력

✔️ 유전자 알고리즘에서 명확히 할 것

1. 부호화 : 문제의 해를 염색체로 어떻게 표현할 것인가? (중요!)
2. 모집단의 크기는 몇 개로 할지?
3. 현재 모집단에서 부모가 될 개체 쌍을 어떻게 선택할 것인지?
   (랜덤하게 할 수 있지만, 좋은 적합도의 개체를 선택)
4. 교배 : 부모의 형질을 어떻게 자식에게 전할 것인지?
5. 돌연변이 : 어떻게 자식의 형질에 돌연변이를 발생시킬 것인지?
6. 어떤 종료 조건 쓸 것인지?

1️⃣ 유전자알고리즘 예제

유전자 알고리즘으로 비선형계획문제와 외판원 문제를 풀어보자.

✔️ 비선형계획문제와 외판원 문제에 사용할 파라미터

1. 부호화 : 문제마다 다르다. (해인 염색체를 어떻게 표현?)
2. 모집단의 크기 : 10개 (대규모 문제일 때는 이것보다 더 커야 함)
3. 적합도가 큰 5개 중 랜덤하게 4개 선택, 적합도 낮은 5개 중 랜덤하게 2개 선택 (총 6개 선택)
4. 교배 : 부모의 형질 전달 방법으로 문제마다 다름
5. 돌연변이 비율 : 자식에서 돌연변이가 발생할 확률 0.1 (대규모 문제일 때에는 이보다 작은 값 사용함)
6. 5번의 반복횟수 동안 목적함수 값의 변화가 없으면 종료

✔️ 1. 비선형계획문제

아래 비선형 문제를 풀어보자.

$Maximize \ f(x) = 12x^5 - 975x^4 + 28,000x^3 - 345,000x^2 + 1,800,000x$
$subject \ to \ 0 \le x \le 31. \ x \ is \ integer$

부호화

유전자 알고리즘은 보통 문자열(염색체)로 해를 표현한다. 여기에서는 정수를 이진화 하여 표현한다. x가 최대 31이니, 이를 이진화 하면 11111이 된다. 따라서 자릿수는 5개로 설정하고 이진화한다.

교배

교배는 부모의 유전자를 비교해 일치하면 형질을 자식에게 넘겨주고, 다른 경우에는 랜덤하게 넘겨준다.
즉, 부모가 정수 3과 10이라고 해보자. 그럼 같은 자릿수에 둘 다 0이면 자식도 0, 둘 다 1이면 1을 물려준다. 이때, 자식은 꼭 두 개체여야 한다. (개체 수 유지를 위해)

# 부모 개체
p1 =  3 = 00011 
p2 = 10 = 01010

# 자식 개체
c1 = 0_01_ 
c2 = 0_01_

그리고 빈칸은 0과 1중 랜덤하게 채워 넣는다. 여기에서는 아래와 같이 결정됐다고 하자.

# 자식 개체
c1 = 01011  => 11
c2 = 00010  => 2

돌연변이

이렇게 자식을 만들고, 확률적으로 돌연변이를 준다. 여기에서는 자식의 유전자 10개에 대해 각각 0.1의 확률로 랜덤하게 형질을 바꾼다. c2의 세 번째 값이 0->1로 바뀌었다.

# 자식 개체
c1 = 01011  => 11
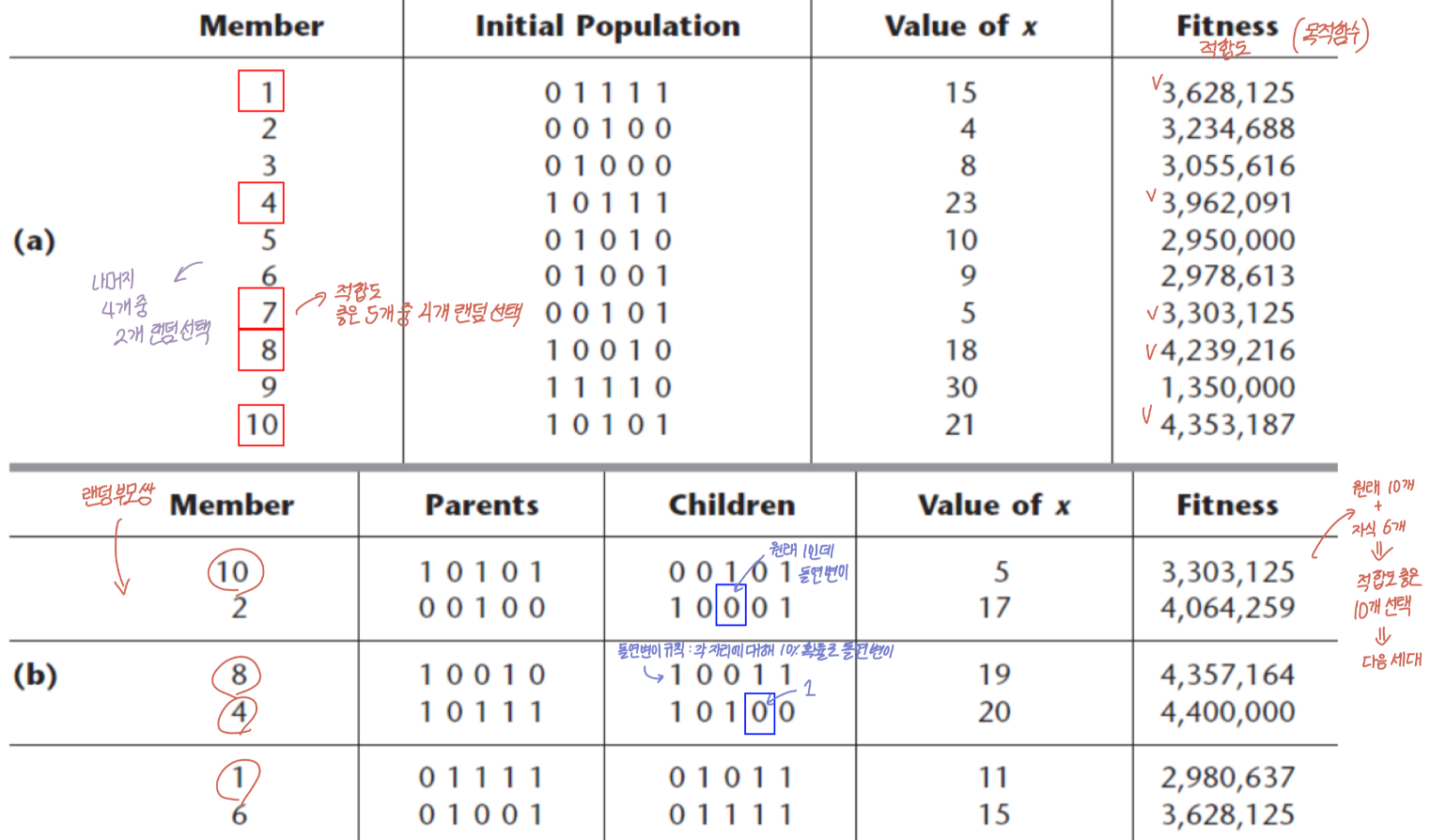
c2 = 00110  => 6

이런 과정으로 작성하면 아래와 같다.

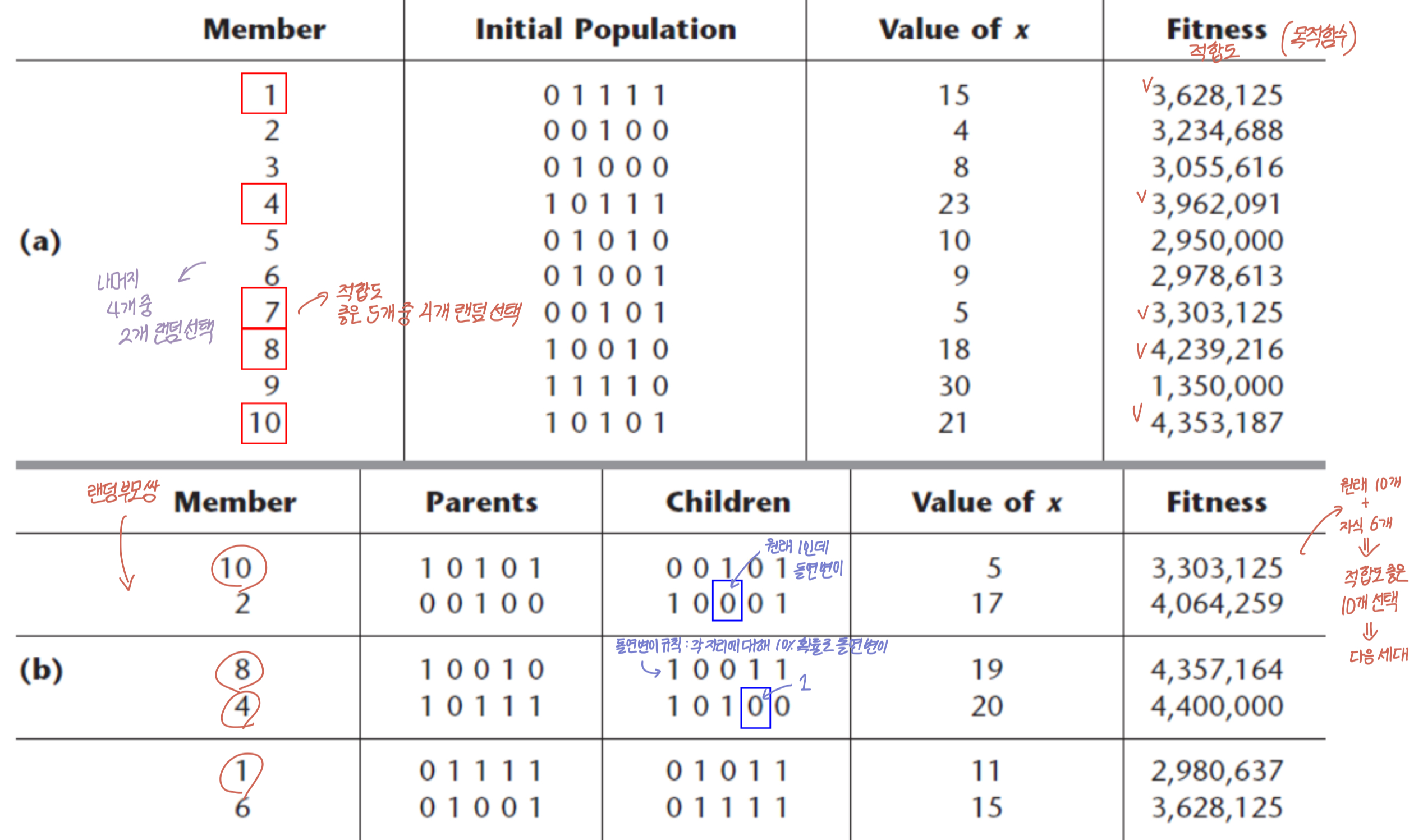
• 이렇게 만들어진 자식 6개체, 원래 있던 부모 10개체 중, 적합도가 좋은 10개의 개체를 다음 세대의 모집단으로 선정한다.

연속형 변수의 이진화
위처럼 정수조건이 없고, 실수일 때는 어떻게 할까?
실수도 이진화가 가능하다.

✔️ 2. 외판원 문제

외판원 문제란? => 여기 클릭

부호화

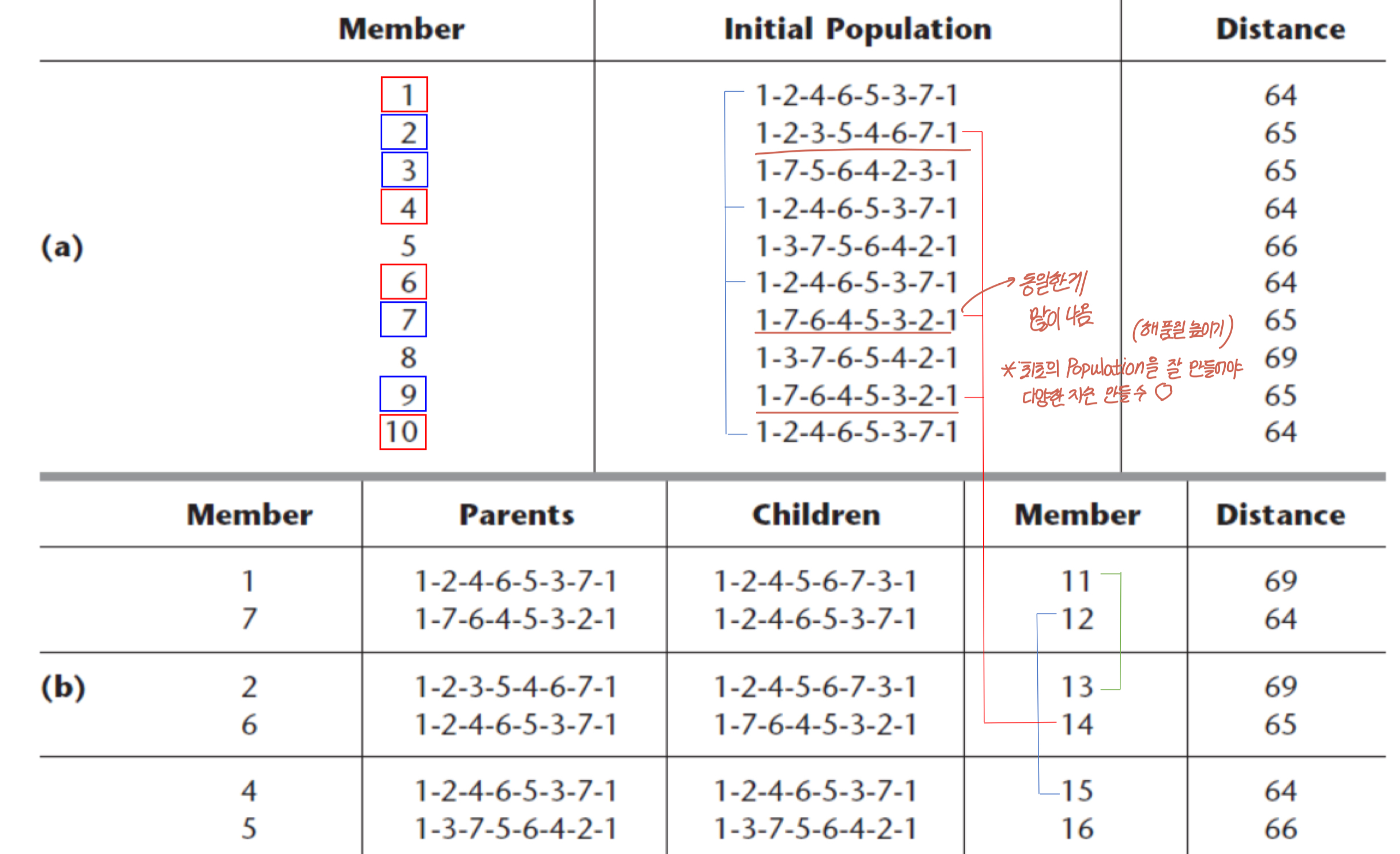
방문하는 도시를 순서대로 적은 문자열(염색체)로 해를 표현한다.

p1 = 1-2-3-4-5-6-7-1
p2 = 1-2-4-6-5-7-3-1

교배

c1과 c2는 어떻게 만들 수 있을까? 아래와 같은 방법으로 만들어낼 수 있다.

• 우선 시작 도시는 1, 그리고 1과 연결된 도시인 2,7,3번 도시 중 랜덤하게 선택한다
  • 2 선택 -> c1 : 1-2
• 이제 2와 연결된 도시중에 아직 방문하지 않은 3,4번 도시 중 랜덤하게 선택
  • 4 선택 -> c1 : 1-2-4
• 4와 연결된 도시 중 아직 방문하지 않은 3,5,6중 선택
  • 3 선택 -> c1 : 1-2-4-3
• 3과 연결된 도시를 선택해야 하는데, p1에서 연결된 도시가 없음. 3-4를 하위경로역순을 통해 뒤집고, 5를 후보로 선택함. p2에서는 후보로 7 선택
  • 5 선택 -> c1 : 1-2-4-3-5
• 5와 연결된 도시 중 아직 방문하지 않은 6,7 중 선택
  • 6 선택 -> c1 : 1-2-4-3-5-6
• 남은 도시는 7, 마지막으로 1이랑 연결
  • 자식 -> c1 : 1-2-4-3-5-6-7-1

돌연변이

0.1의 확률로 돌연변이를 만든다. 이 문제에서는 돌연변이를 아래와 같이 만든다.

후보도시 중, 랜덤하게 하나를 선택하는데 이때 0.1의 확률로 선택된 도시를 제외하고 다시 랜덤하게 남은 도시 중 하나를 선택한다.

위 예제에서는, 처음에 1과 연결된 도시 2,7,3번 중 하나를 랜덤하게 고르게 되는데 이때 2가 선택됐다. 0.1의 확률로 돌연변이가 일어났다고 하면, 선택된 2를 제외하고 7,3번 중에서 하나를 랜덤하게 생성하게 된다.

번식 요약

위 과정을 요약하면 아래와 같다.

1. 초기화
출발도시 1 선정
2. 다음 도시 후보 선택
각 부모에서 출발도시와 연결된 도시를 후보로 선택. 출발도시와 연결된 도시가 없는 경우 하위경로역순을 통해 연결할 도시 선택
3. 다음 도시 선택
2에서 얻은 후보 도시 중 랜덤하게 하나 선택
4. 돌연변이 검사
랜덤수를 발생하여 돌연변이 확률보다 작으면 3에서 선택한 도시 거절. 2에서 얻은 나머지 후보 도시 중 하나를 랜덤하게 선택
5. 계속
현재 도시에 연결할 수 있는 후보도시를 찾아 경로를 완성. 즉, 모든 경로가 완성될 때까지 2-4번 반복
6. 완성
실행불가능한 경로이거나 더 이상 도시를 연결할 수 없을 때에는 1단계부터 다시 수행하여 실행가능한 경로를 찾는다.