그래프란?

---

1. 그래프의 기본개념

• 그래프 : 그래프란 연결 데이터를 저장할 수 있는 자료구조이다.

우리에게 가장 익숙한 연결관계는 위치 데이터이다. 아래처럼 위치들이 연결된 것을 볼 수 있다.

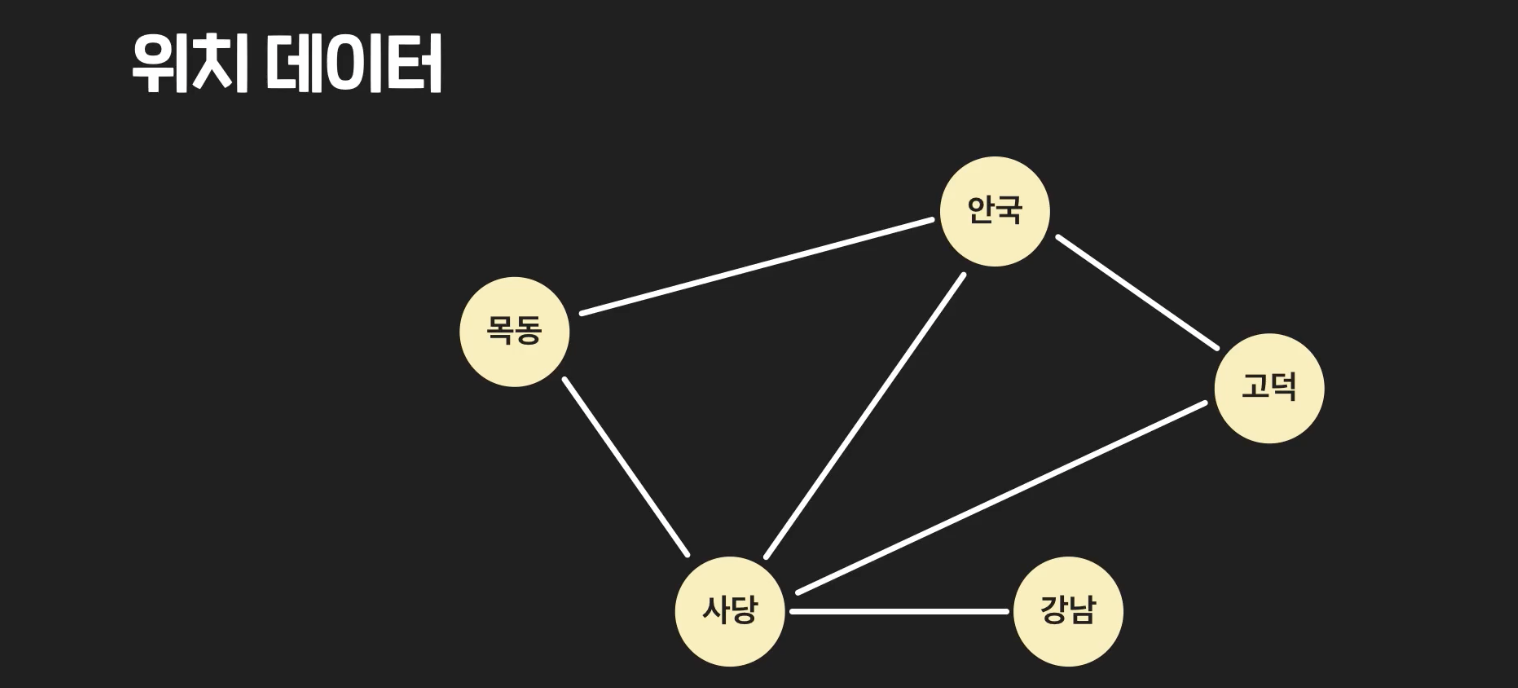
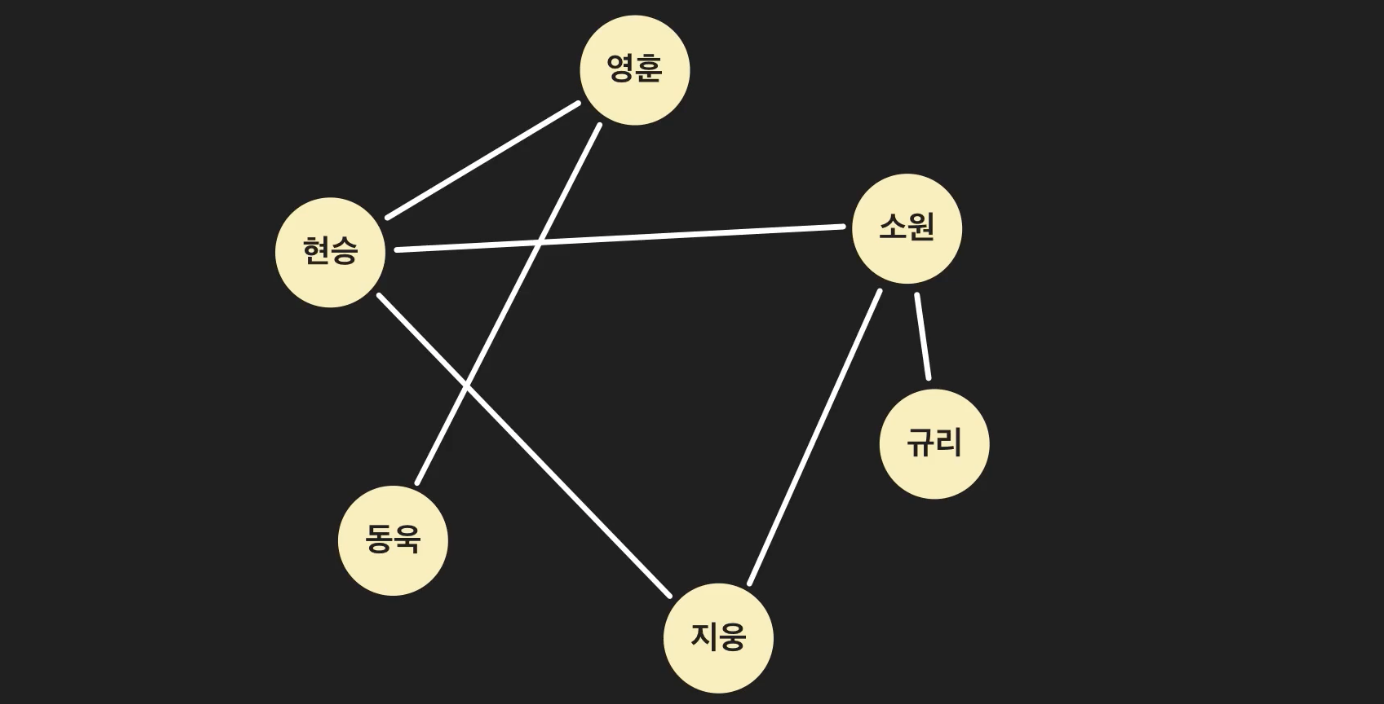
아래는 사회연결망 그래프이다.

• 엣지 : 노드를 잇는 선은 엣지라고 한다.
  

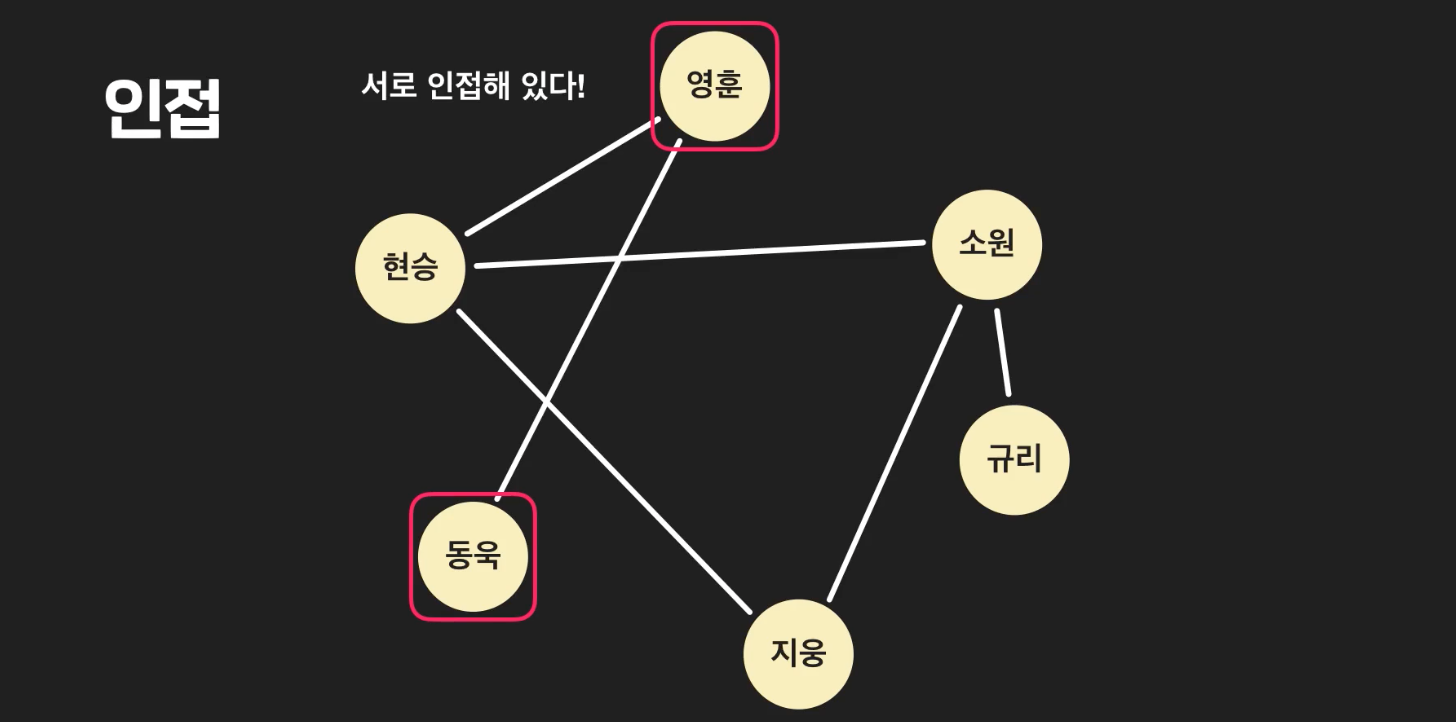
• 인접 : 아래처럼 영훈과 동욱이 엣지로 연결되어 있는 경우, 서로 인접해 있다고 표현한다.

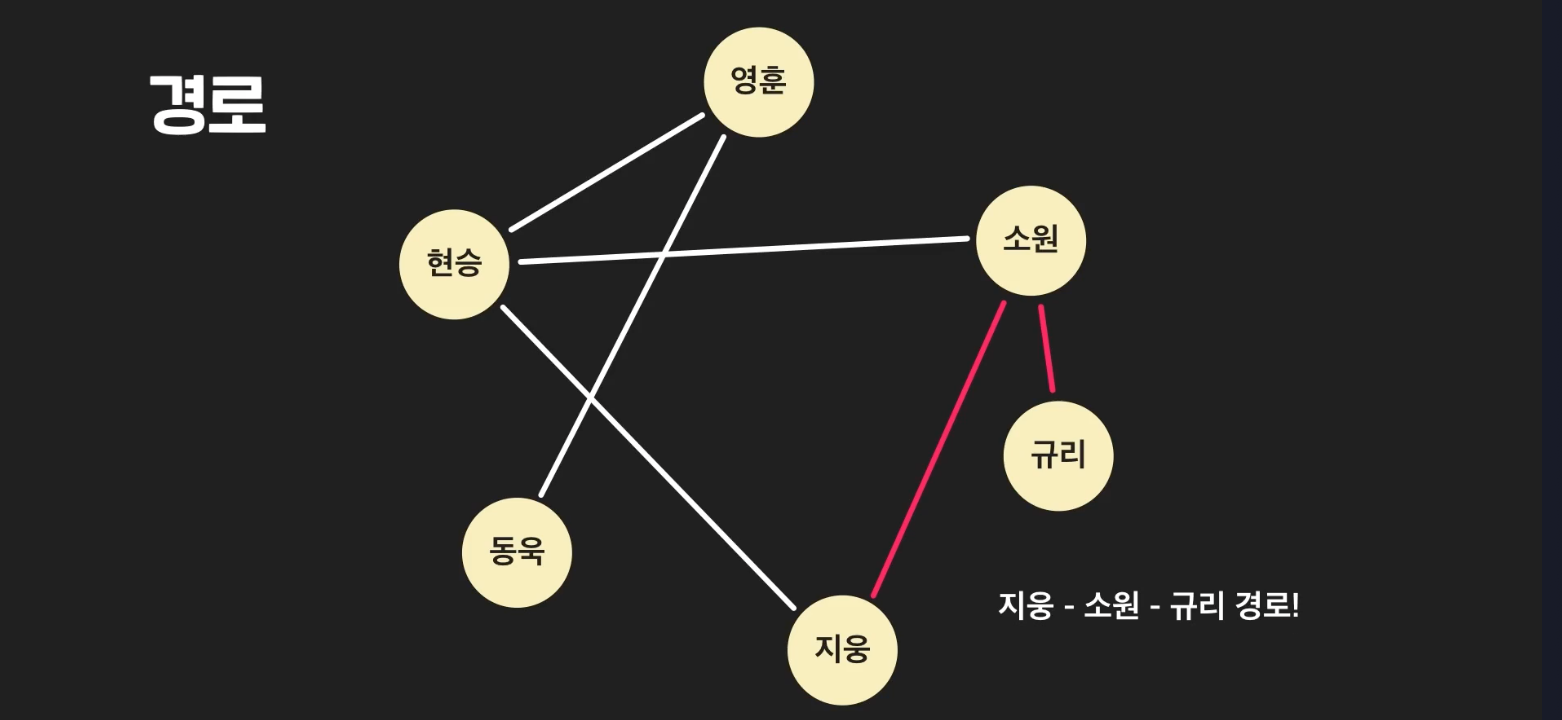
• 경로 : 아래처럼 지웅과 규리는 인접해 있지는 않지만, 소원을 통해 연결되므로, '지웅-소원-규리' 경로를 통해 연결됐다고 표현한다.
  

• 최단경로 : 두 노드들 사이에 가장 거리가 작은 경로를 최단경로 라고 한다.

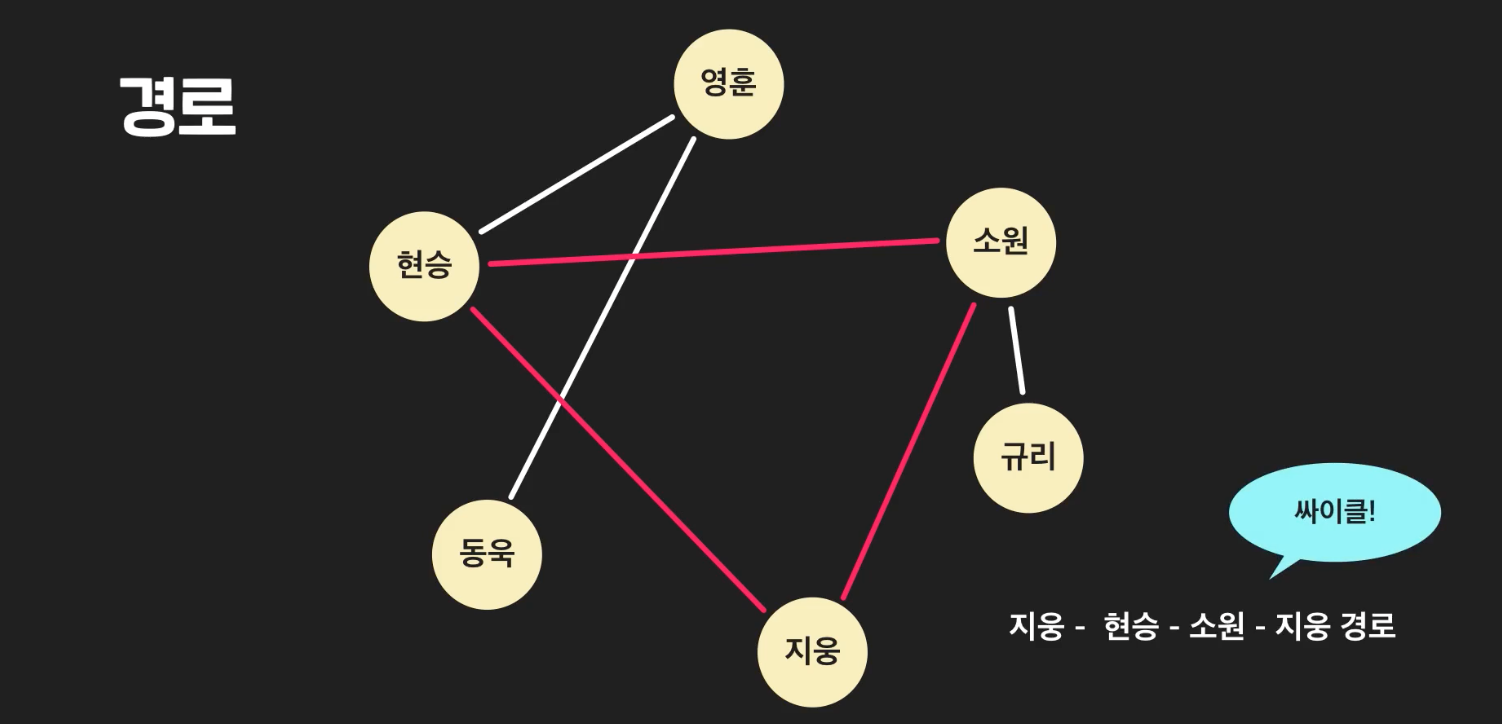
• 사이클 : 특정 노드에서 다시 그 노드로 돌아오는 경로는 사이클 이라고 한다.
  

• 차수 : 한 노드가 가지고 있는 엣지의 수를 차수라고 한다. 현승은 세 친구와 연결되어 있으니 차수가 3이다. 차수를 이용하면 노드에 대해 유용한 데이터를 알아낼 수 있다. 이 경우에는 차수가 각 노드의 친구의 수를 나타낸다.

• 무방향 그래프 : 그래프에서는 방향이 있는데, 위 친구 예시에서는 양방향이므로 오히려 그냥 방향이 없다고 이야기할 수도 있다. 이런 경우를 무방향 그래프(undirected graph)라고 한다. 이 경우 (현승, 지웅)과 (지웅, 현승)은 똑같다.

• 방향 그래프 : 인스타그램에서는 누군가 나를 팔로우하면 방향이 생긴다. 이런 경우, 방향 그래프라고 하며, 방향그래프에서는 엣지가 떠나는 노드를 항상 앞에 쓰고 들어가는 노드를 뒤에 적어준다. 현승이가 지웅이를 팔로우하면, (현승, 지웅)과 같이 적는다.
  방향 그래프에서는 차수를 출력차수 와 입력차수로 나누어서 생각한다.
  

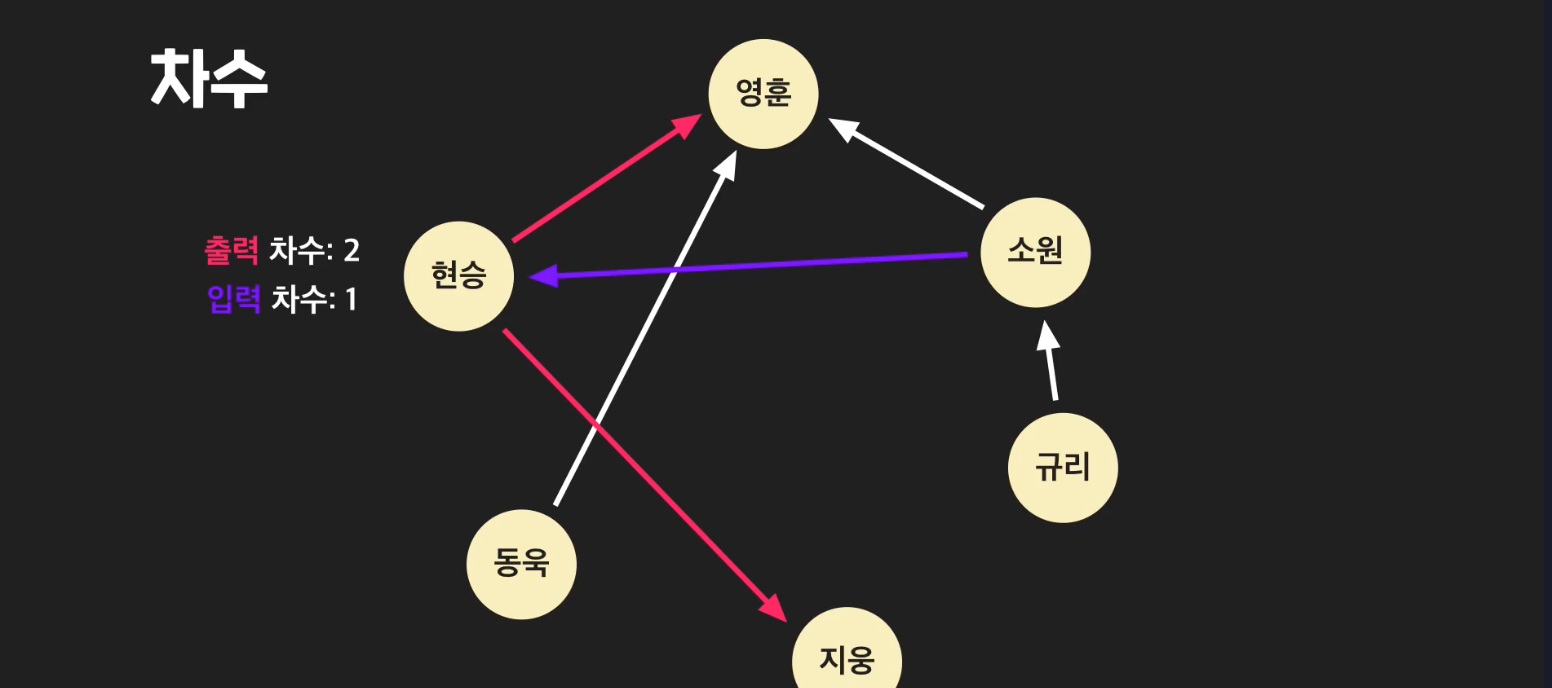
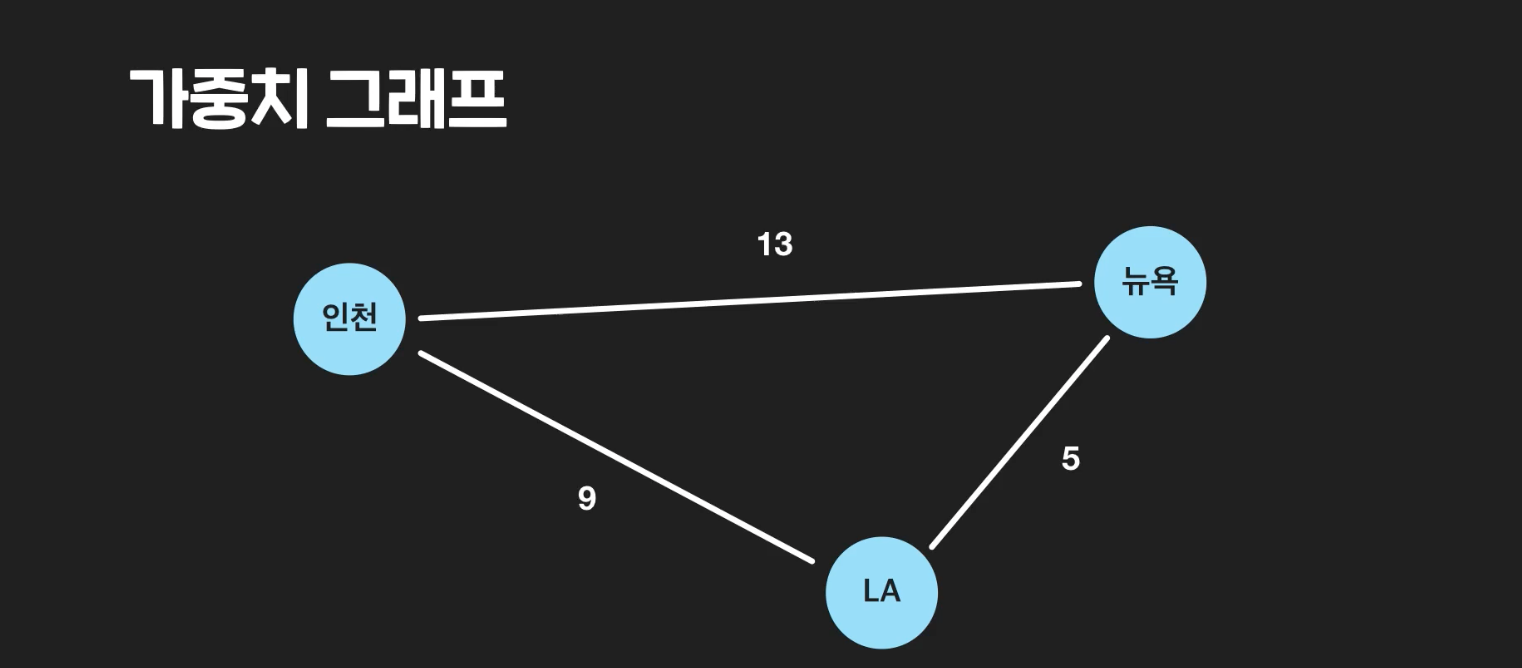
• 가중치 그래프 : 각 공항끼리 이동시간을 가중치로 나타낼 수 있는데, 이런 그래프를 가중치 그래프라고 한다. 가중치 그래프에서의 거리는 경로에 있는 엣지의 가중치의 합이다.
  

• 무가중치 그래프 : 모든 엣지의 값이 동일한 그래프는 무 가중치 그래프라고 부른다. 무가중치 그래프에서의 거리는 단순히 경로에 있는 엣지의 수이다.

그래프 구현

그래프 구현에서는 노드를 구현하는 방법과 엣지를 구현하는 방법으로 나눠서 본다.
노드를 구현하는 방법 먼저 보자. 지하철 역 노드를 나타내는 클래스를 구현해보자.

class StationNode:
  """지하철 역 노드를 나타내는 클래스"""
  def __init__(self, name, num_exits):
    self.name = name
    self.num_exits = num_exits

# 지하철 역 노드 인스턴스 생성
station_0 = StationNode('교대역', 14)
station_1 = StationNode('사당역', 14)
station_2 = StationNode('종로3가역', 16)
station_3 = StationNode('서울역', 16)

링크드리스트에는 헤드노드, 트리의 경우엔 루트노드가 존재하는데, 연결고리를 나타내는 그래프에서는 일반적으로 모든 노드가 동등한 위치에 있다.
그러니 항상 모든 노드에 바로 접근할 수 있도록 만들어준다. 이렇게 할 수 있는 두 가지 방법이 있다. 배열이나 해시테이블에 저장하는 방법이다. O(1)으로 접근할 수 있어 효율적이다.
1. 노드들을 배열 또는 동적배열에 저장한다. (파이썬에서는 자료형 리스트)

# 노드들을 파이썬 리스트에 저장
stations = [station_0, station_1, station_2, station_3]
# 인덱스로 바로 접근 가능
stations[3]

2. 노드들을 해시 테이블에 저장한다. (파이썬에서는 딕셔너리)

• 다만 이 키는 겹치면 안 되는 제약이 있으므로 주의해야 한다.

# 지하철 역 노드들을 파이썬 딕셔너리에 저장
stations = {
    '교대역':station_0,
    '사당역':station_1,
    '종로3가역':station_2,
    '서울역':station_3
}

# 교대역에 접근하고 싶으면,
node_1 = stations['교대역']

엣지구현 1 : 인접행렬

이번에는 그래프의 엣지를 구현하는 방법중 하나인 인접행렬을 알아보자.
인접행렬은 노드들의 연결관계(엣지)를 나타내는 2차원 리스트이다.

• 인접행렬 만드는 법
  1. 각 노드를 리스트에 저장해 고유 정수 인덱스를 준다.
  2. 노드수x노드수 크기의 행렬을 만든다.
  3. 노드들의 엣지 유무 및 가중치에 따라 행렬의 요소를 채운다.

예시를 살펴보자.

• 아래와 같이 연결이 되어 있으면 1, 아니면 0으로 나타내는 행렬이다.
  대각성분을 보면 다 0인데, 노드가 본인 자신에게는 연결이 되지 않았다고 보는 것이다. 또, 대칭행렬임을 알 수 있다.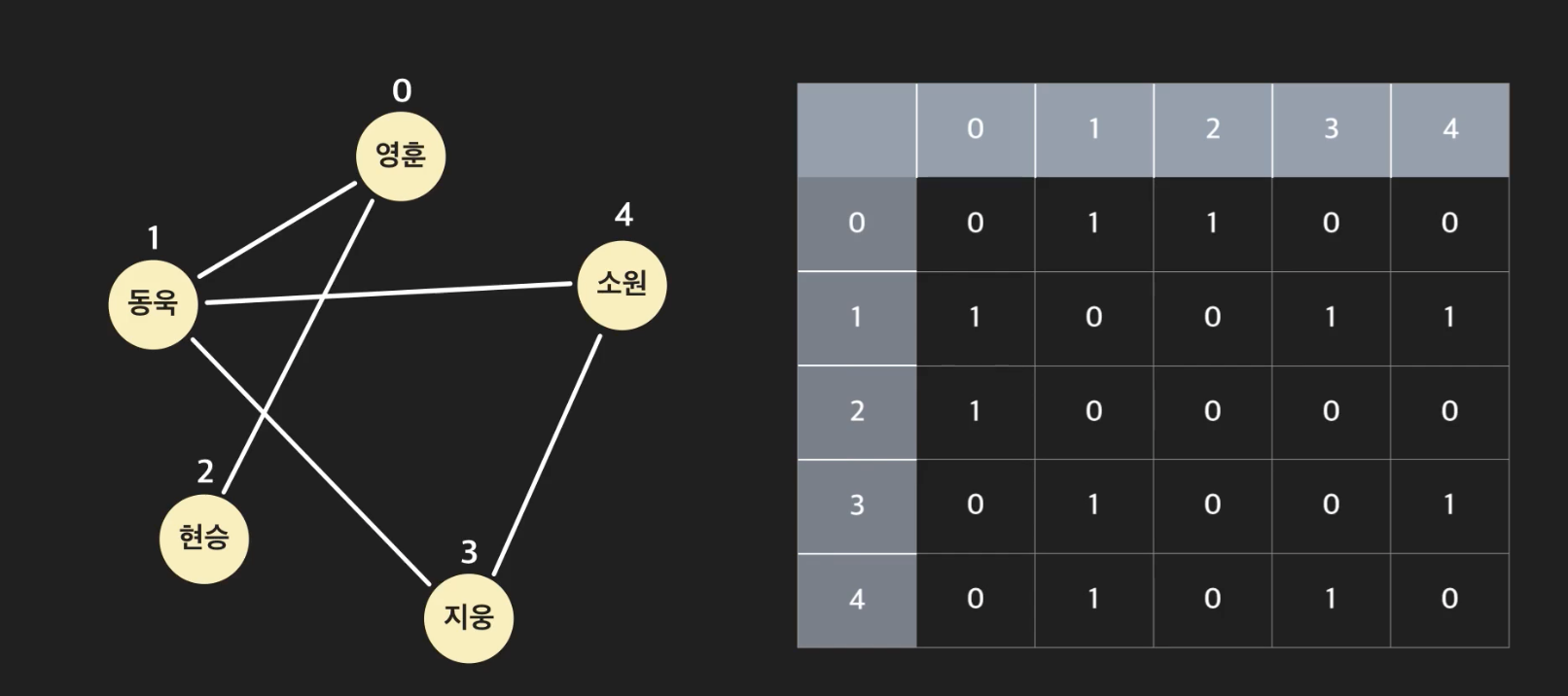

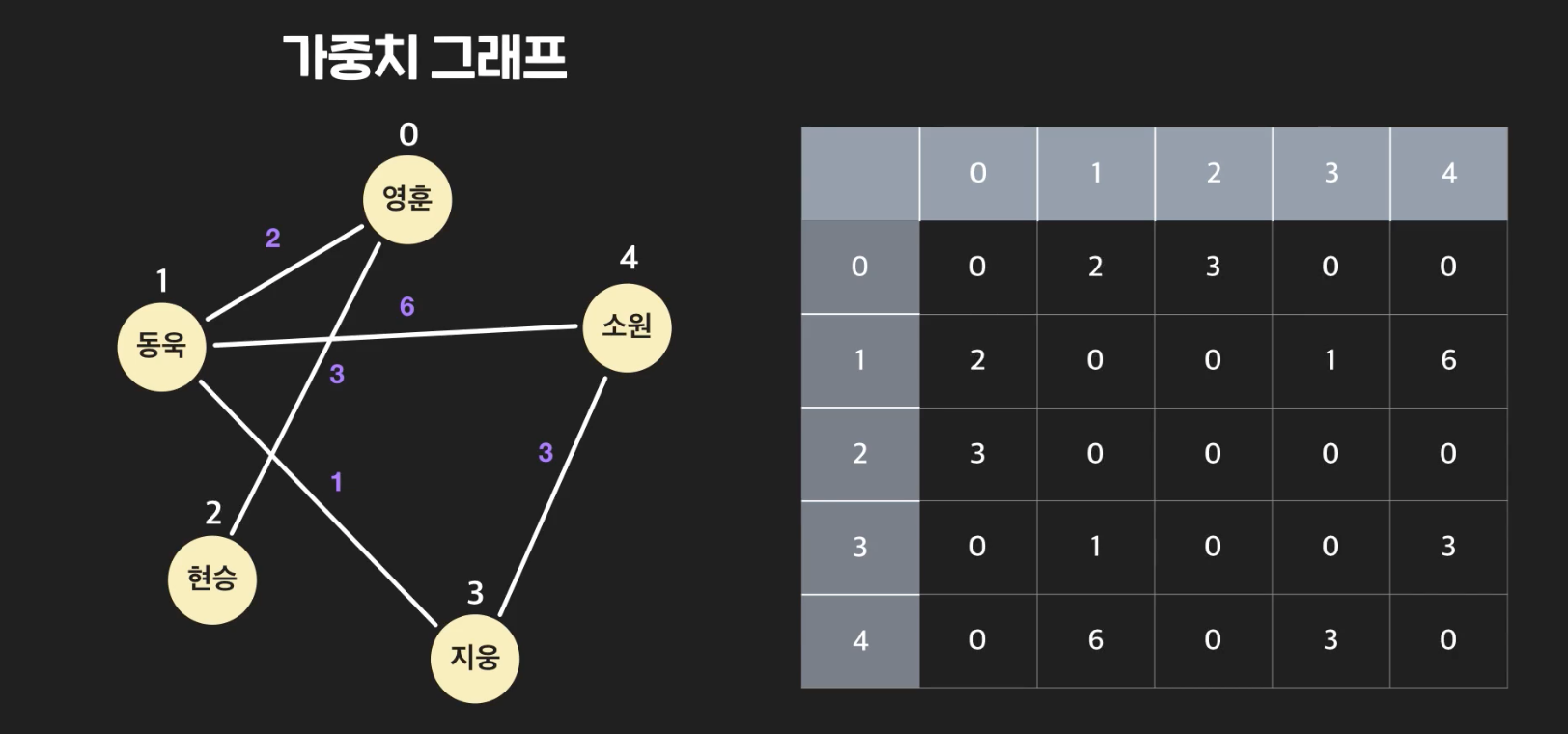
• 가중치 그래프의 인접행렬은 이렇게 표현가능하다.

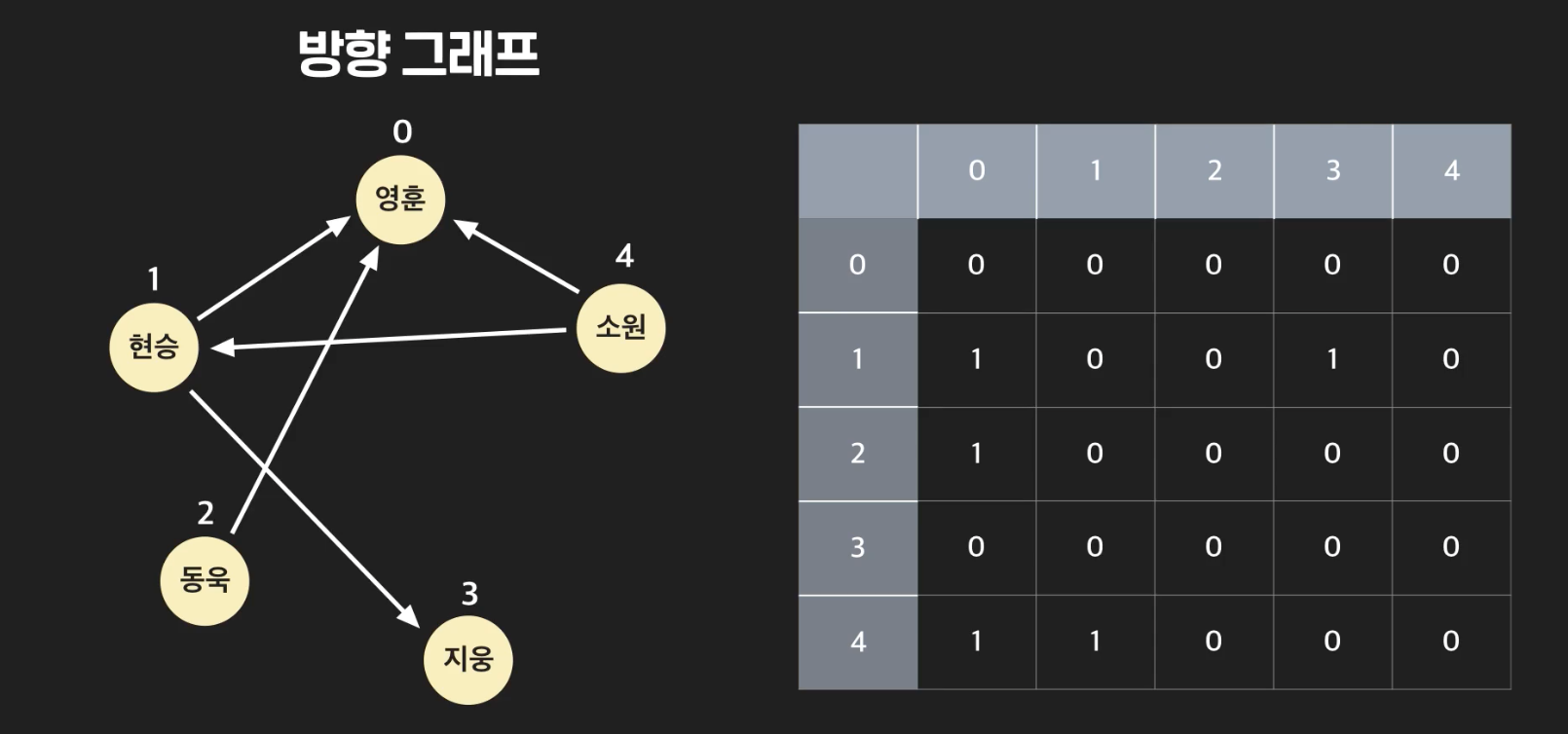
• 방향그래프의 인접행렬이다. 현승(1)은 영훈(0)을 가리킨다. 따라서 (1, 0)에는 1이 들어가지만, (0,1)에는 0이 들어갔다. 방향그래프는 대각선을 기준으로 대칭적이지 않다.

엣지구현 2 : 인접 리스트

이번에는 엣지를 구현하는 또 다른 방법인 인접 리스트를 알아보자.

• 인접 리스트
  • 각 노드의 엣지를 리스트에 저장하는 방법

아래 역 그래프에서 역 이름을 key로, 노드 인스턴스를 value로 써서 파이썬 딕셔너리에 저장했다고 해보자.

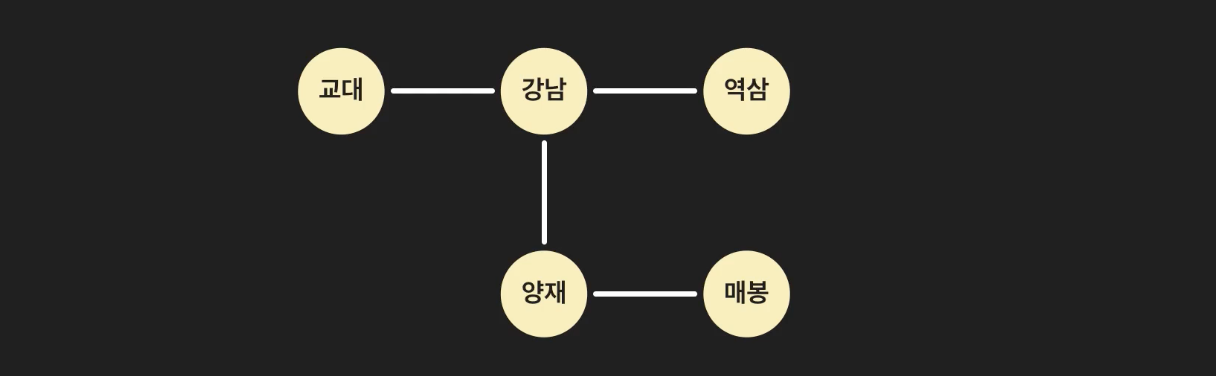
그리고 노드 클래스에 self.adjacent_stations = []를 추가해준다.
위 예시로 보면 강남의 'adjacent_stations' 는 [stations['교대'], stations['역삼'], stations['양재']]이다.

class StationNode:
  """지하철 역 노드를 나타내는 클래스"""
  def __init__(self, name, num_exits):
    self.name = name
    self.num_exits = num_exits
    self.adjacent_stations = []

인접리스트는 한 노드가 연결된 다른 노드들에 대한 레퍼런스를 저장한다.

• 방향그래프에서는 위와 같이 A -> B 일 때, A의 인접리스트에 B를 추가하고, B의 인접리스트에는 A를 넣지 않는다.

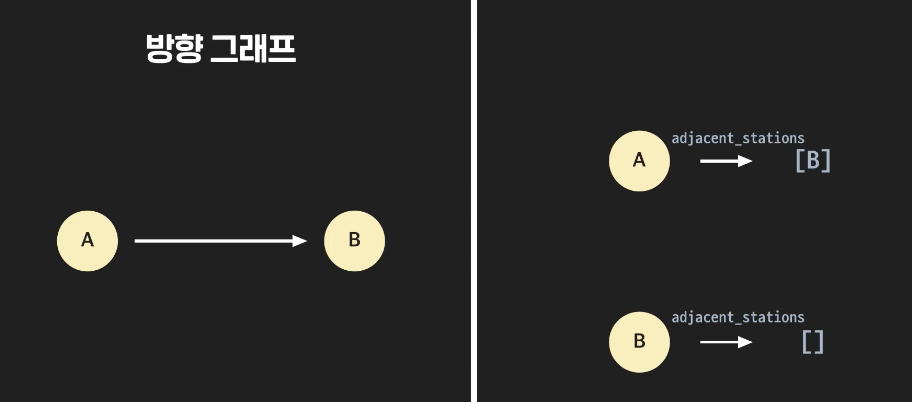
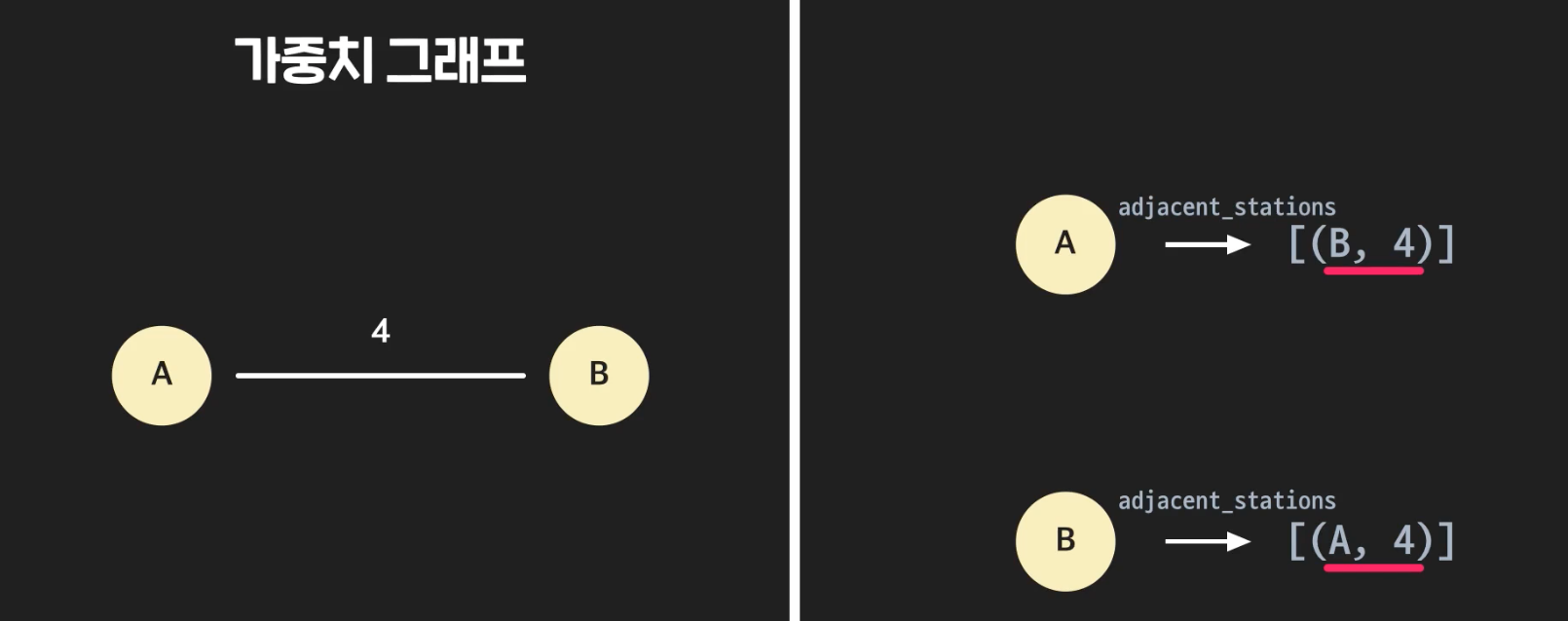
• 가중치 그래프는 이렇게 튜플을 넣어준다.

복잡도 표현 기호

보통 다른 자료구조에서 데이터 수를 $n$이라고 하고, 이를 이용해 효율성을 나타내곤 했는데, 그래프에서는 다른 기호들을 사용한다.

• $V$ 란?

  • $V$는 그래프 안에 있는 모든 노드들의 집합이다.
  • 그래프에서의 노드를 Vertex라고도 부르고, 이것의 첫 알파벳을 딴 거다.

• $E$ 란?

  • $E$는 그래프 안에 있는 모든 엣지들의 집합니다.
  • Edge의 첫 알파벳을 땄다.

• $V$와 $E$의 관계

  • 노드 수가 $V$일 때, 그래프 안에는 최대 몇 개의 엣지가 있을까?
    • 무방향 그래프는 $V^2/2$, 방향 그래프는 $V^2$의 엣지를 가진다.
    • 따라서 $E$는 최악의 경우 $V^2$에 비례한다.

• 노드를 저장하는 공간

  • 노드의 개수를 $V$로 나타내므로 $O(V)$의 공간을 사용한다.

• 인접행렬이 차지하는 공간

  • “총 노드의 수 x 총 노드의 수” 만큼의 행렬을 만드므로, $O(V^2)$의 공간을 사용한다.

• 인접리스트가 차지하는 공간

  • 엣지를 저장하는 공간 : 무방향 그래프일 때 $2E$, 방향 그래프일 때 $E$이므로, $O(E)$이다.
  • 인접리스트 자체를 저장하는 데 $O(V)$, 엣지를 저장하는 데 $O(E)$ 이므로 총 $O(E+V)$만큼의 공간을 사용한다고 표현한다.

• 인접 행렬에서 인접한 노드들을 가지고 오려면 항상 길이가 $V$인 배열(파이썬 리스트)를 돌아야 한다. 인접 리스트를 쓰면 인접한 노드만 들어 있는 배열을 돌아서 가지고 올 수 있죠. 대부분의 경우 이 리스트는 길이가 $V$ 보다 짧다. 그렇기 때문에 인접한 노드들을 가지고 올 때는 인접 리스트를 사용하는 게 더 효율적이다.