0️⃣ 위상정렬이란?
위상정렬(Topological Sorting)이란 아래처럼 사이클이 없는 유향그래프를 일열로 나열하는 문제이다. 각 노드가 생산과정에서 하나의 Task라고 보면, e를 하기 위해서는 b와 d가 선행되어야 하고, b를 하기 위해서는 a가 선행되어야 한다. 이런 순서를 정해주는 거라고 보면 된다. 아래처럼 위상정렬의 결과는 여러 개일 수 있다.

-
입력 조건
싸이클이 없는 유향 그래프
->DAG(Directed Acyclic Graph)라고 한다. -
위상정렬(Toplogical Sorting) 특징
모든 정점을 일렬로 나열하되, 정점x와 정점 y로 가는 간선이 있으면 x는 반드시 y보다 앞에 위치해야 한다. 일반적으로 임의의 유향그래프에 대해 복수의 위장정렬 해가 존재한다.
1️⃣ 위상정렬 알고리즘 1
수도코드
topologicalSort1(G)
{
for 1 to n {
진입간선이 없는 정점 u를 선택한다;
A[i] <- u;
정점 u와, u의 진출간선을 모두 제거한다;
}
// 이 시점에서 배열 A[1..n]에 정점들이 위상정렬 되어 있다.
}- 위 수도코드를 보면서 그린 예시다. 진입간선이 없는 정점 u을 찾고, A에 넣은 다음, 그 u에서 나가는 화살표를 지워나간다.
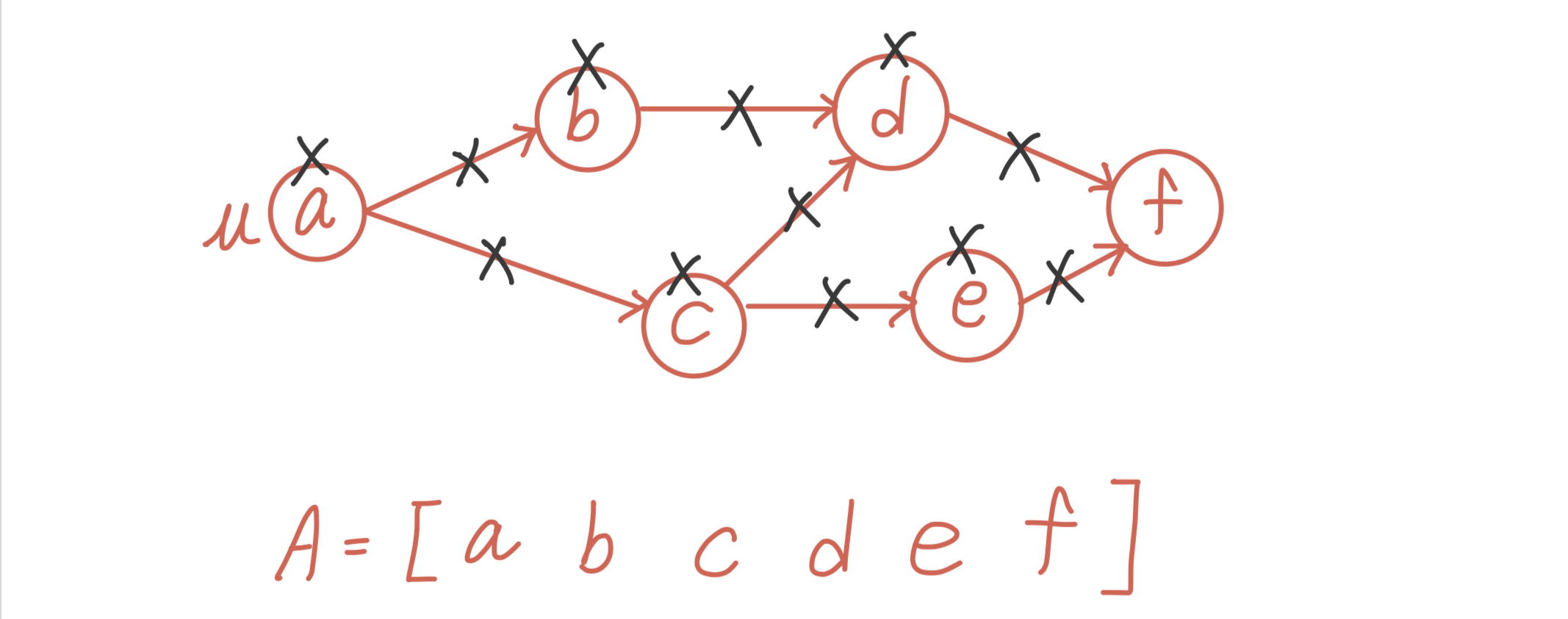
파이썬 구현
def topologicalSort1(G):
A = []
k = len(G)
while len(A) != k:
to_list = []
for i in G.values():
to_list += i
# 진입간선이 없는 정점 리스트
u_list = set(G.keys()) - set(to_list)
if len(u_list) == 0:
return A
for i in u_list:
A.append(i)
del G[i]
return A
# 입력예시 1
adj_list = {0: [2, 3], 1: [3, 4], 2: [3, 5], 3: [5], 4: [5], 5: []}
# 입력예시 2
test_G = {'a': ['b', 'c'], 'b': ['d'], 'c':['d', 'e'], 'd':['f'], 'e':['f'], 'f':[]}
topologicalSort1(adj_list) # [0, 1, 2, 4, 3, 5]
topologicalSort1(test_G) # ['a', 'c', 'b', 'e', 'd', 'f']2️⃣ 위상정렬 알고리즘2
수도코드
topologicalSort2(G)
{
for each v in V:
visited[v] <- NO;
for each v in V:
if (visited[v] = NO) then DFS-TS(v);
}
DFS-TS(v)
{
visited[v] <- YES;
for each x in L(v) // L(v) : v의 인접 리스트
if (visited[x] = NO) then DFS-TS(x);
연결 리스트 R의 맨 뒤에 정점 v를 삽입한다;
}파이썬 코드
def topologicalSort2(G):
R =[]
visited = {i:False for i in G.keys()}
for v in visited:
if visited[v] == False:
DFS_TS(v, G, visited, R)
return R
def DFS_TS(v, G, visited, R):
visited[v] = True
for x in G[v]:
if visited[x] == False:
DFS_TS(x, G, visited, R)
R.insert(0, v)
# 입력예시 1
adj_list = {0: [2, 3], 1: [3, 4], 2: [3, 5], 3: [5], 4: [5], 5: []}
# 입력예시 2
test_G = {'a': ['b', 'c'], 'b': ['d'], 'c':['d', 'e'], 'd':['f'], 'e':['f'], 'f':[]}
print(topologicalSort2(adj_list)) # [1, 4, 0, 2, 3, 5]
print(topologicalSort2(test_G)) # ['a', 'c', 'e', 'b', 'd', 'f']3️⃣ DAG 에서 최단경로 구하기
싸이클이 없는 유향그래프인 DAG에서 최단경로(Shortest Path)를 구할 때, 위상정렬을 사용한다. DAG는 r이라는 출발노드에서 다른 모든 노드까지 각각 최소거리를 구한다. 아래 수도코드를 보자.
수도코드
DAG_shortestPath(G,r) // G: 그래프, r: 출발노드
{
for each u in V:
d_u <- inf;
d_r <- 0;
G의 정점들을 위상정렬한다;
for each u in V: // 위상정렬 순서로
for each v in L(u): // L(u): 정점 u로부터 연결된 정점들의 집합
if (d_u + w_{u,v} < d_v) then d_v <- d_u _ w_{u,v};
}- 가중치가 있는 DAG를 우선 위상정렬을 한다. 일단은 다른 노드까지의 거리를 inf로 설정한다. 아래 예제에서는 노드 b를 시작노드로 설정했기 때문에 본인으로 가는 거리는 0으로 설정한다.
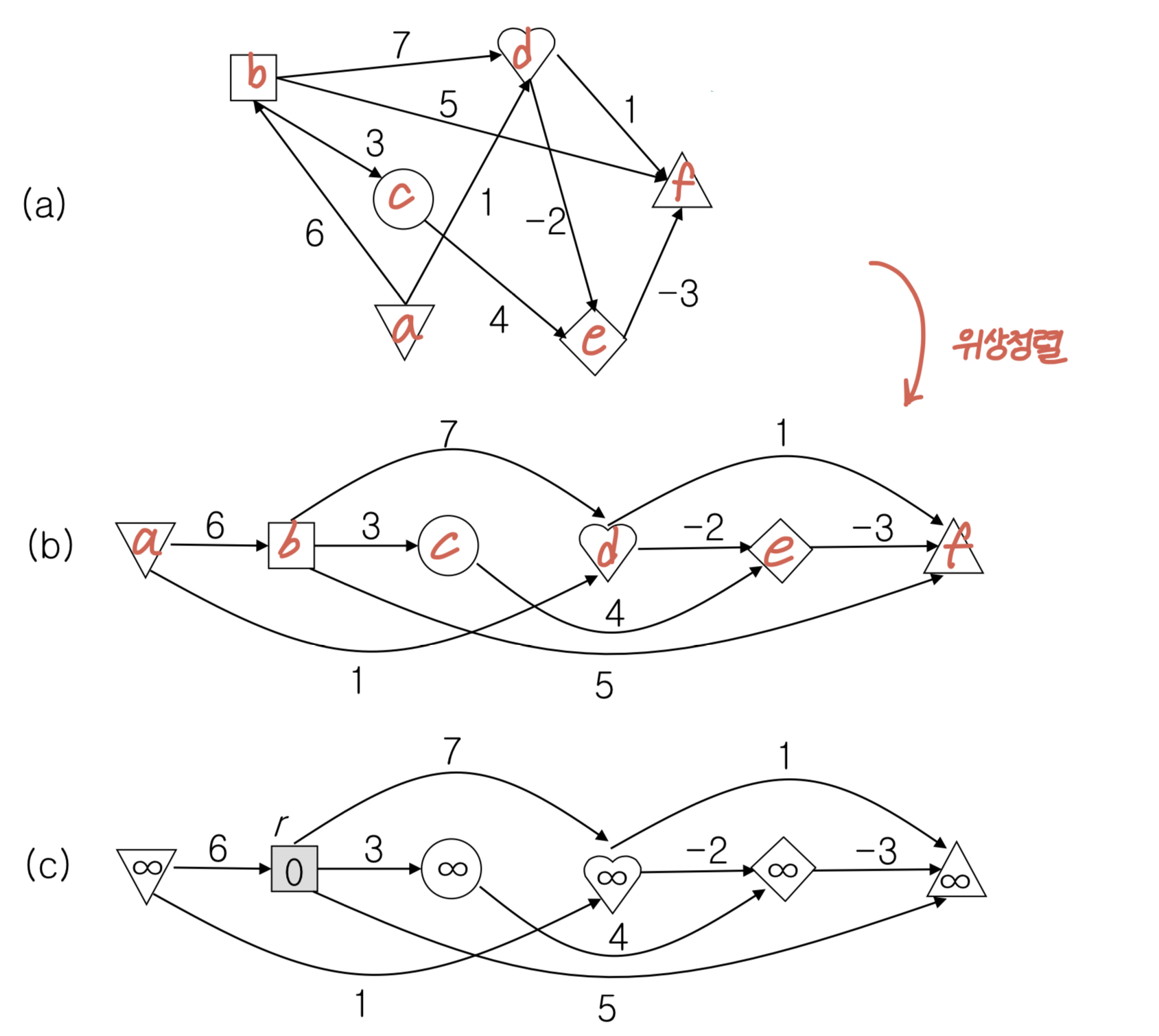
- 그리고 위상정렬된 순서대로 반복문을 돌린다. 각 노드 안에 써 있는 숫자는 그 iteration에 시작노드에서 해당 노드까지 가는 거리를 나타낸다. iteration이 반복되면서 이게 업데이트된다.
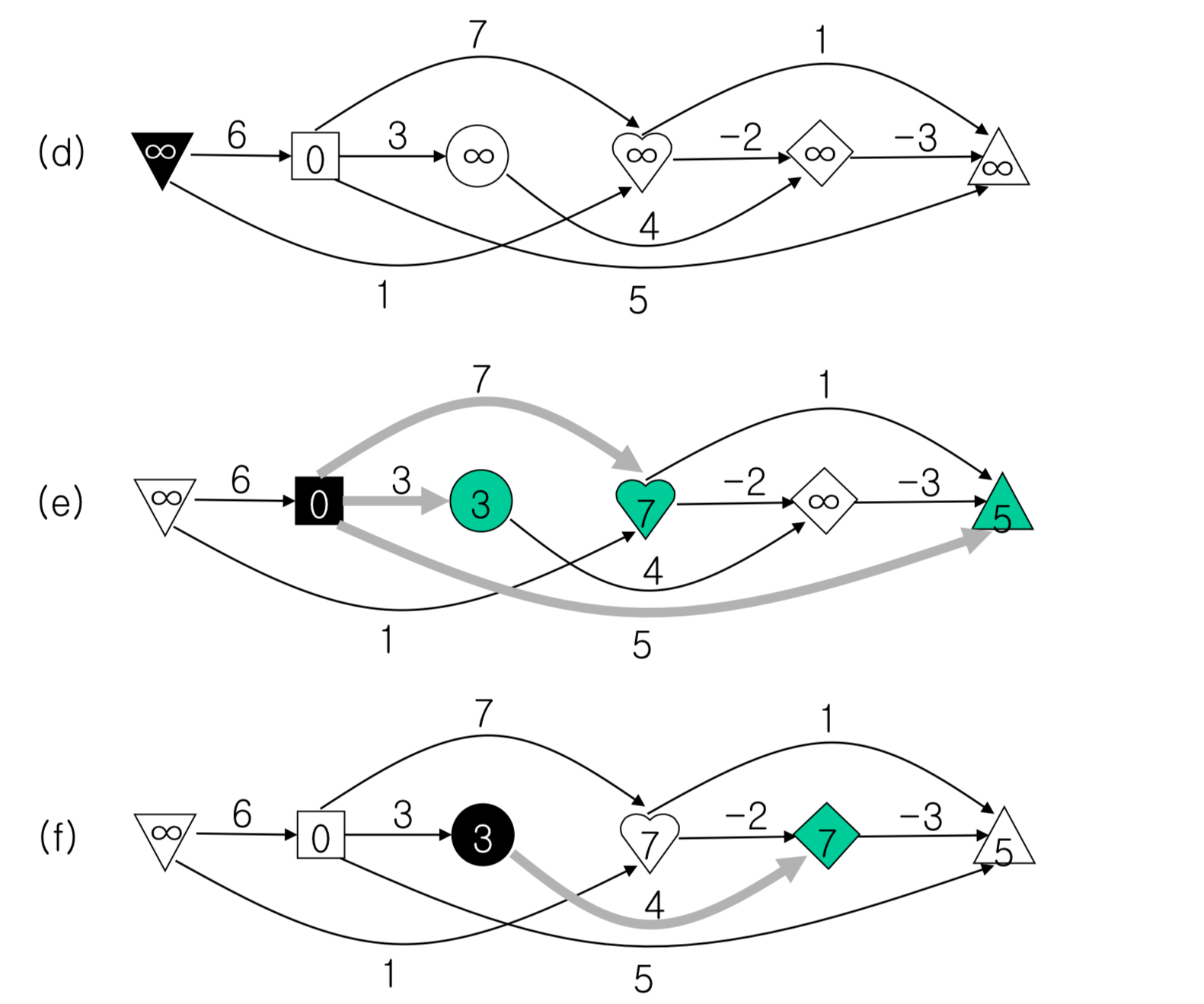
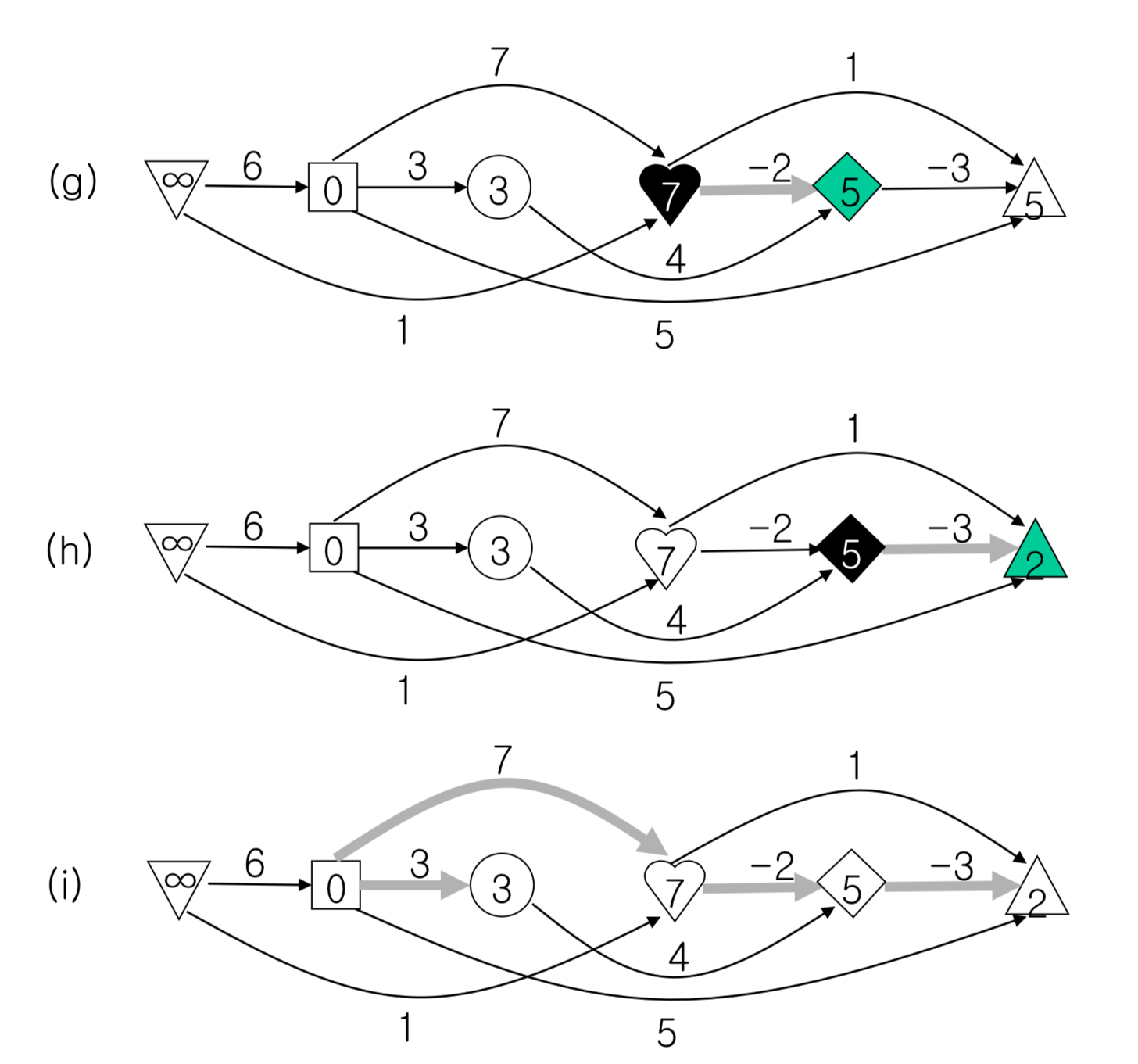
파이썬 코드
import math
def DAG_shortestPath(G, r):
d = {i:math.inf for i in G.keys()}
d[r] = 0
for u in topologicalSort2(G):
for v in G[u]:
if d[u] + G[u][v] < d[v]:
d[v] = d[u] + G[u][v]
return d
# 연결리스트
G = {'a':{'b':6, 'd':1},
'b':{'d':7, 'f':5, 'c':3},
'c':{'e':4},
'd':{'e':-2, 'f':1},
'e':{'f':-3},
'f':{}}
DAG_shortestPath(G, 'b') # {'a': inf, 'b': 0, 'c': 3, 'd': 7, 'e': 5, 'f': 2}