0️⃣ Shortest Path(최단 경로 알고리즘)

이번 글에서는 최단경로 알고리즘 중 BFS로 최단경로 만드는 방법과 Dijkstra 알고리즘을 이해하고, 수도코드를 살펴보고자 한다.
파이썬 코드는 다음번 글에서!!

• 최단경로란? 두 노드 사이 경로 중 가장 거리가 짧은 경로

• 그래프의 특성에 따라 최단 거리 알고리즘이 다르다
  • 방향이 있는지, 가중치는 있는지, 사이클이 있는지, 음수 엣지가 있는지 등, 그래프의 특성에 따라 사용되는 최단 거리 알고리즘이 다르다.

• 최단 경로 알고리즘
  • BFS
    • 비 가중치 그래프에서만 사용 가능
  • Dijkstra(다익스트라) 알고리즘
    • 가중치 그래프에서도 사용 가능

1️⃣ BFS

그래프 탐색을 하기 위한 BFS를 조금만 변경하면 최단 경로 알고리즘으로 만들 수 있다.

BFS 개념은 여기에서 확인 가능!

BFS에서 각 노드는 그 노드를 방문한 적 있는지 없는지 표시한다. 이를 visited 라는 변수로 표현해줬다.
최단 경로 알고리즘에서는 predecessor라는 변수를 추가해준다. predecessor는 '~이전의 것'을 의미하는데, 특정 노드에 오기 직전의 노드를 의미한다.

아래 그림처럼, B와 C로 오기 직전의 노드는 A이다. 따라서 왼쪽 표처럼 표시해줄 수 있다.

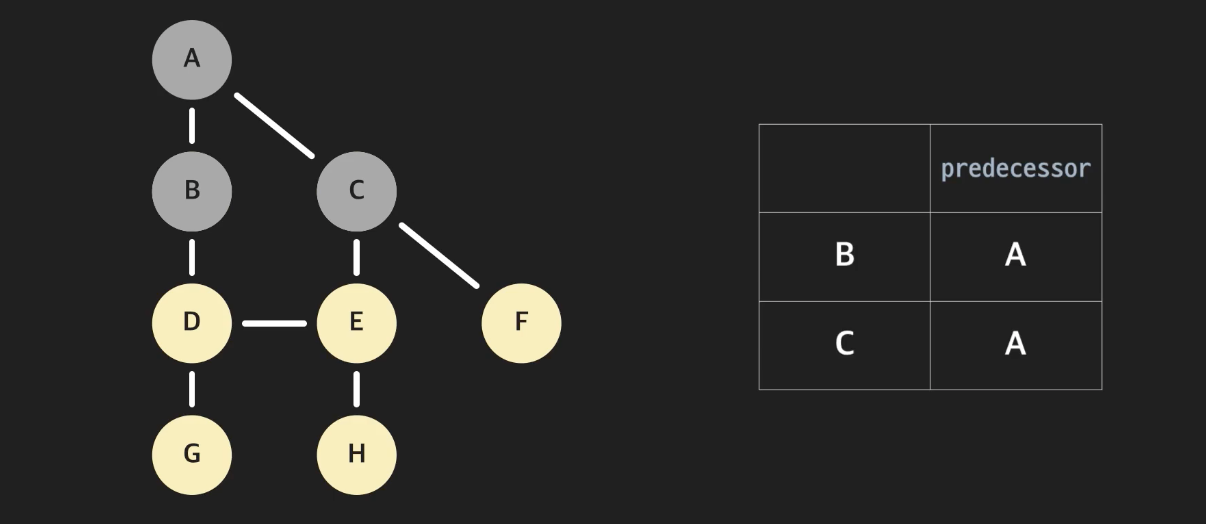
BFS알고리즘에 따라 Predecessor 표가 어떻게 채워지는지 하나씩 살펴보자. BFS는 뒤로 들어가고, 앞으로 나가는 큐를 사용한다.

• 우선 시작 노드인 A를 방문표시하고, predecessor는 None으로 표시한다. 이후에 큐에 넣어준다.
  

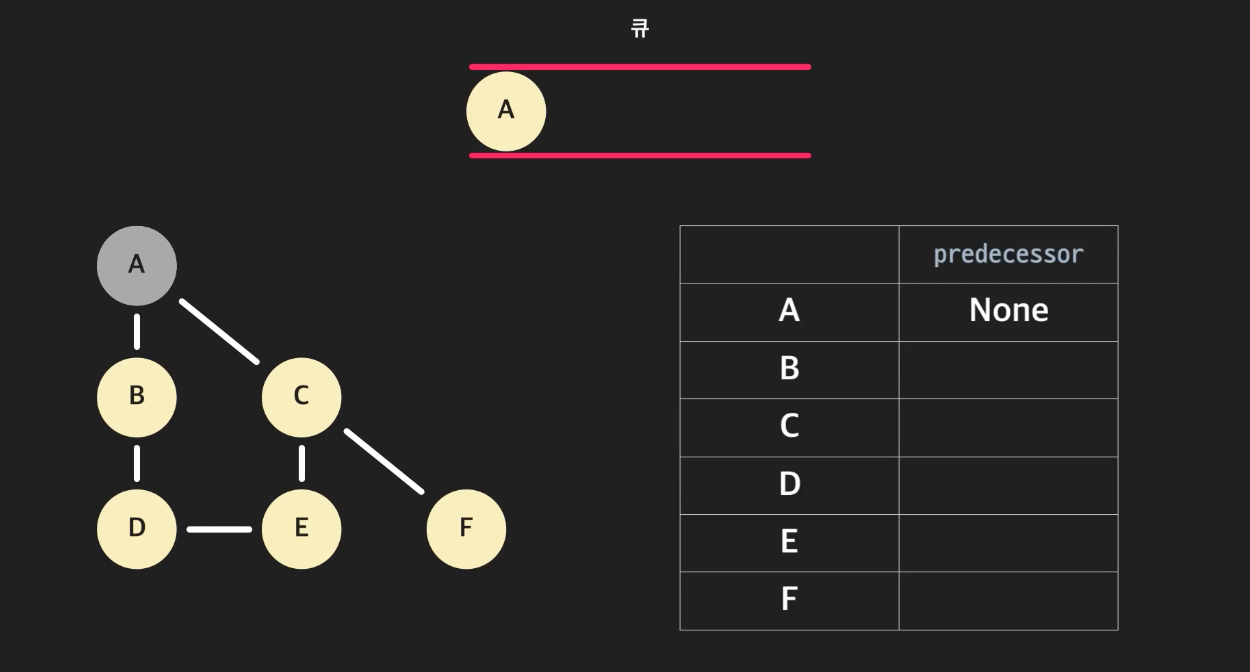
• 큐에서 A를 뽑고, A와 인접한 노드인 B를 큐에 넣어준다. B의 predecessor는 A가 된다. 마찬가지로 C도 큐에 넣고, predecessor는 A로 지정한다.

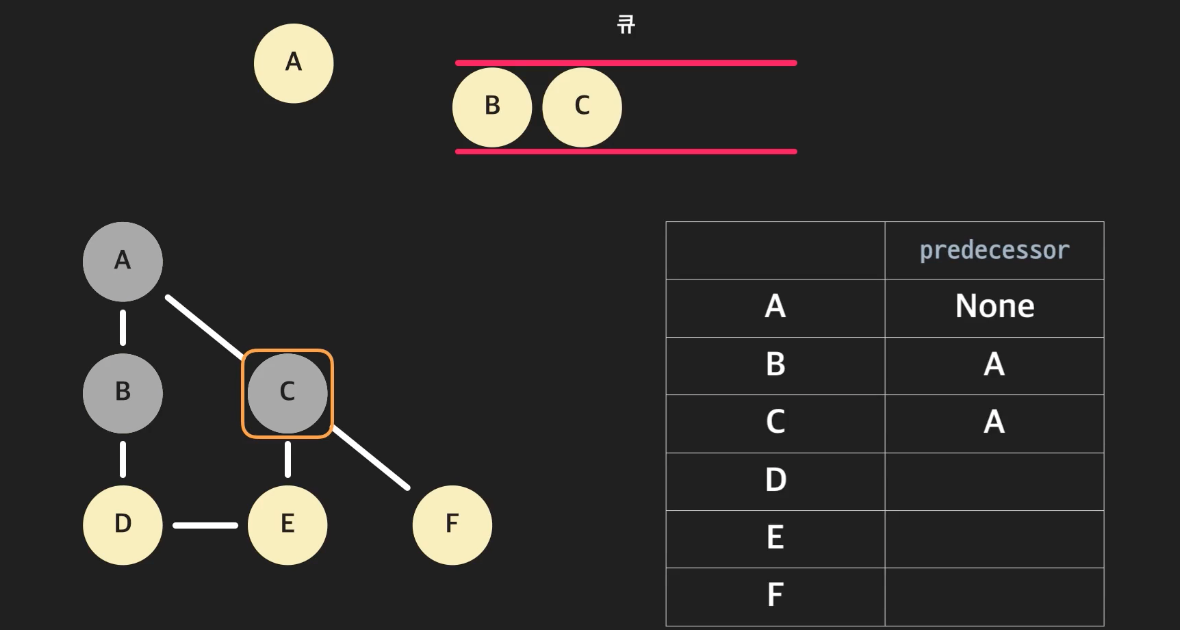
• 이제 큐에 앞에 있는 B를 뽑고 B와 인접한 노드이며, 아직 방문하지 않은 D를 큐의 뒤쪽으로 넣어준다. predecessor는 B로 표시한다. 또, 큐 앞에 있는 C를 뽑고, 아직 방문하지 않은 E를 큐에 추가, F를 추가, predecessor는 C로 설정한다.
  

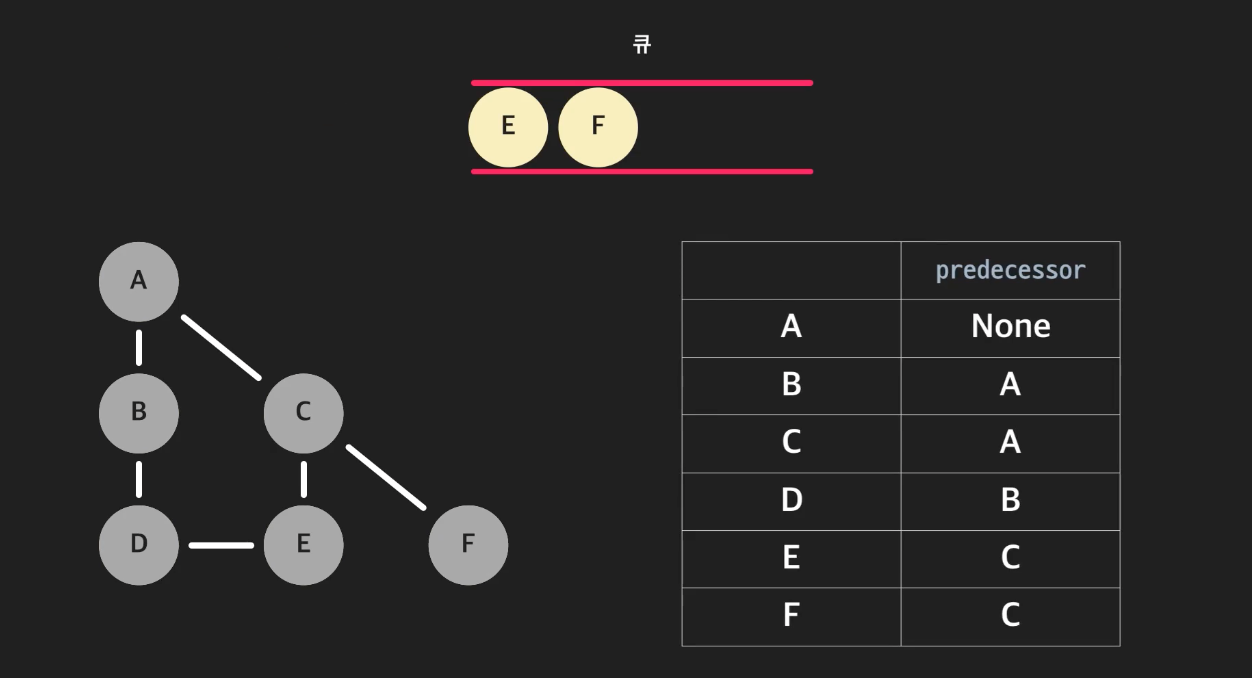
• 큐에서 E, F를 꺼내고, 둘 다 인접한 노드 중 방문하지 않은 노드가 없으므로 BFS가 종료된다.

이제 어떻게 최단경로를 알 수 있을까?
A에서 F까지의 최단 경로를 구한다고 해보자.
F에서부터 A까지 거꾸로 올라가면 되는데, A의 predecessor는 C, C의 predecessor는 A로, A까지 온다. 즉, 이 순서를 거꾸로 하면, A -> C -> F가 최단 경로이다. 이렇게 거꾸로 찾아가는 것을 Backtracking이라고 한다.

BFS 수도코드
이를 일반화해서 정리하면 다음과 같다.

시작 노드를 방문 표시 후, 큐에 넣는다.
큐에 아무 노드가 없을 떄까지:
	큐 가장 앞 노드를 꺼낸다.
    꺼낸 노드에 인접한 노드들을 모두 보면서:
    	처음 방문한 노드면:
        	방문한 노드 표시를 해준다.
            predecessor 변수를 큐에서 꺼낸 노드로 설정
            큐에 넣어준다.

Backtracking 수도코드

현재 노드를 경로에 추가한다.
현재 노드의 predecessor로 간다.
predecessor가 없을 때까지 위 단계를 반복

코드잇 BFS 최단 경로용으로 바꾸기

from collections import deque
from subway_graph import *

# 코드를 추가하세요
def bfs(graph, start_node):
    """최단 경로용 bfs 함수"""
    queue = deque()  # 빈 큐 생성

    # 모든 노드를 방문하지 않은 노드로 표시, 모든 predecessor는 None으로 초기화
    for station_node in graph.values():
        station_node.visited = False
        station_node.predecessor = None

    # 시작점 노드를 방문 표시한 후 큐에 넣어준다
    start_node.visited = True
    queue.append(start_node)
    
    while queue:  # 큐에 노드가 있을 때까지
        current_station = queue.popleft()  # 큐의 가장 앞 데이터를 갖고 온다
        for neighbor in current_station.adjacent_stations:  # 인접한 노드를 돌면서
            if not neighbor.visited:  # 방문하지 않은 노드면
                neighbor.visited = True  # 방문 표시를 하고
                queue.append(neighbor)  # 큐에 넣는다
                neighbor.predecessor = current_station


def back_track(destination_node):
    """최단 경로를 찾기 위한 back tracking 함수"""
    res_str = destination_node.station_name  # 리턴할 결과 문자열
    while destination_node.predecessor != None:
        res_str = destination_node.predecessor.station_name + " " +  res_str
        destination_node = destination_node.predecessor
    return res_str.strip()

stations = create_station_graph("./new_stations.txt")  # stations.txt 파일로 그래프를 만든다

bfs(stations, stations["을지로3가"])  # 지하철 그래프에서 을지로3가역을 시작 노드로 bfs 실행
print(back_track(stations["강동구청"]))  # 을지로3가에서 강동구청역까지 최단 경로 출력

BFS로 찾은 경로가 최단 경로가 되는 이유?

• 방문하는 순서를 보면, 처음으로 방문하는 B와 C는 시작점에서 거리가 1인 노드들이다.
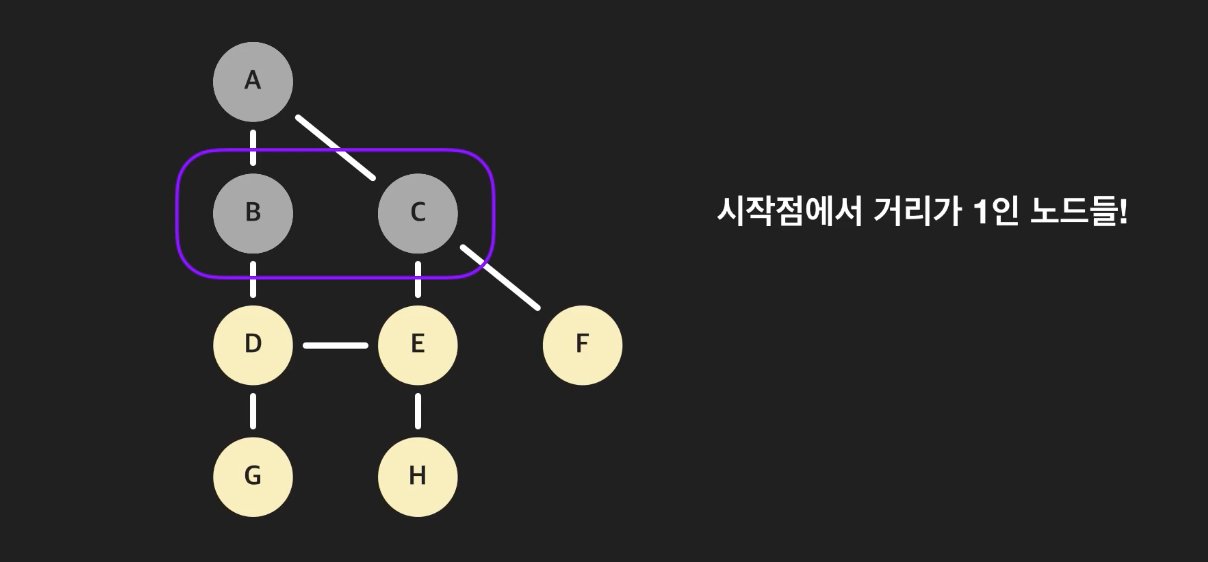
• 이후에 방문하는 노드들 D, E, F는 시작점에서 거리가 2인 노드들이다.
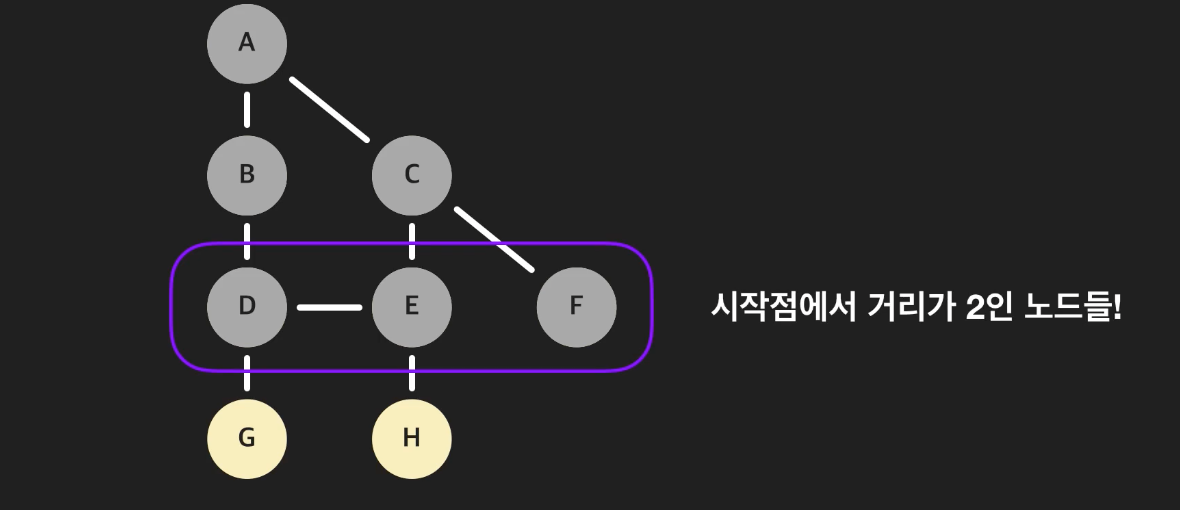
• 마찬가지로 다음으로 방문하는 G와 H는 시작점에서 거리가 3인 노드들이다.
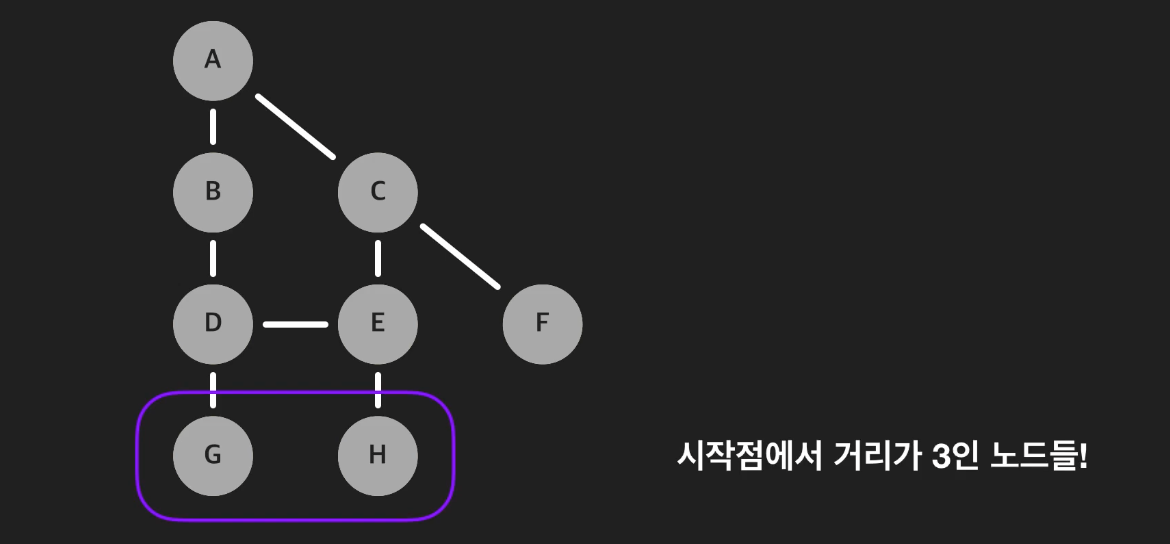
• 이런 순서로 방문하기 때문에, F를 방문하는 순간에 거리가 1인 노드들은 이미 다 방문했고, 거리가 2인 노드들을 방문한다는 것을 안다. F를 처음 방문한 순간이 F를 가장 빠르게 찾은 순간이 된다. 그래서 이때, F까지의 predecessor를 통해 최단경로를 찾을 수 있다.

2️⃣ Dijkstra 알고리즘

가중치 그래프의 최단 경로를 구하기 위한 알고리즘이다. 다익스트라 알고리즘을 사용하기 위해서는 그래프 노드에 아래 3가지 변수를 저장해야 한다.

• distance : 시작점에서 이 노드까지의 거리를 저장한다. 노드까지 오는 여러 경로가 있으므로, 이 값이 업데이트된다. 따라서 특정 노드까지의 '최단 거리 예상치'라고 할 수 있다.
• predecessor : 현재까지의 최단 경로에서 바로 직전의 노드를 저장한다. 위와 마찬가지로 업데이트된다.
• complete : 노드까지의 최단 경로를 찾았다고 표시하는 변수다. 처음에 모두 False로 설정하고, 확실한 최단경로를 찾으면 True로 표시한다.

다익스트라 알고리즘에서는 노드를 하나씩 방문한다.
노드들을 방문하면서 해당 노드의 distance, predecessor 변수들을 업데이트해주는데, 이것을 relaxation이라고 한다. A에서 B로 방문할 때, B의 변수를 업데이트 해주는 걸 '엣지(A, B)를 relax 한다'고 표현한다.

이제 다익스트라 알고리즘을 하나씩 살펴보자. 먼저 predecessor는 None, distance는 무한대로 초기화한다. 아직 방문한 노드들도 없기 때문에 complete도 False로 초기화한다.

• 우선 시작노드인 A의 distance는 0, predecessor는 None으로 둔다. 그리고 A의 엣지들을 보는데, 이때 연결된 엣지의 노드가 complete된 노드면 건너뛴다. 아직 complete된 노드가 없으므로, 엣지(A, B)와 (A, C)를 다 relax해주면 된다. B의 distance는 4, predecessor는 A로 설정한다. C의 distance를 1로 바꾸어주고, predecessor는 A로 설정한다. 이제 A의 complete 변수를 True로 설정한다.
  

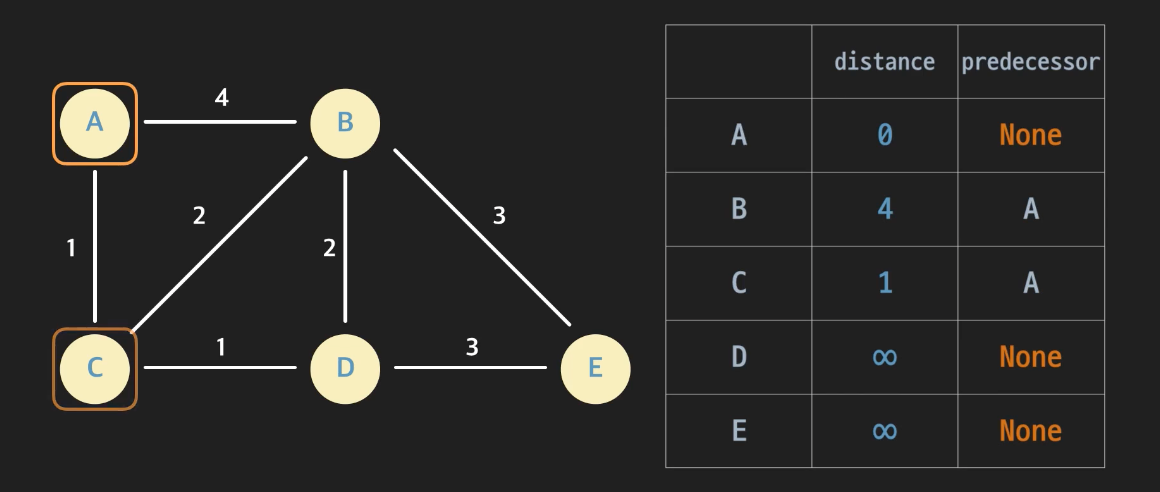
• 다음은 complete되지 않은 노드 중 distance가 가장 작은 노드를 고른다. distance가 1인 C를 고르면 된다. 위에서 했던 것과 같이 C의 엣지를 모두 relax해준다. (C, B)와 (C, D)를 relax해준다. 이제 C를 complete표시해준다.

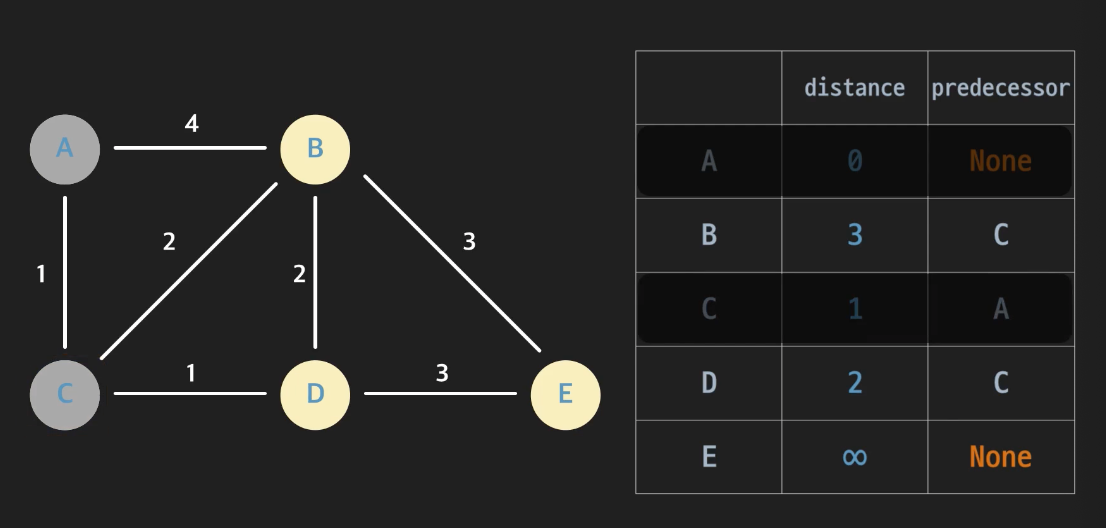
• 다음으로 complete되지 않고 distance가 가장 작은 D 노드에 대해 진행한다.

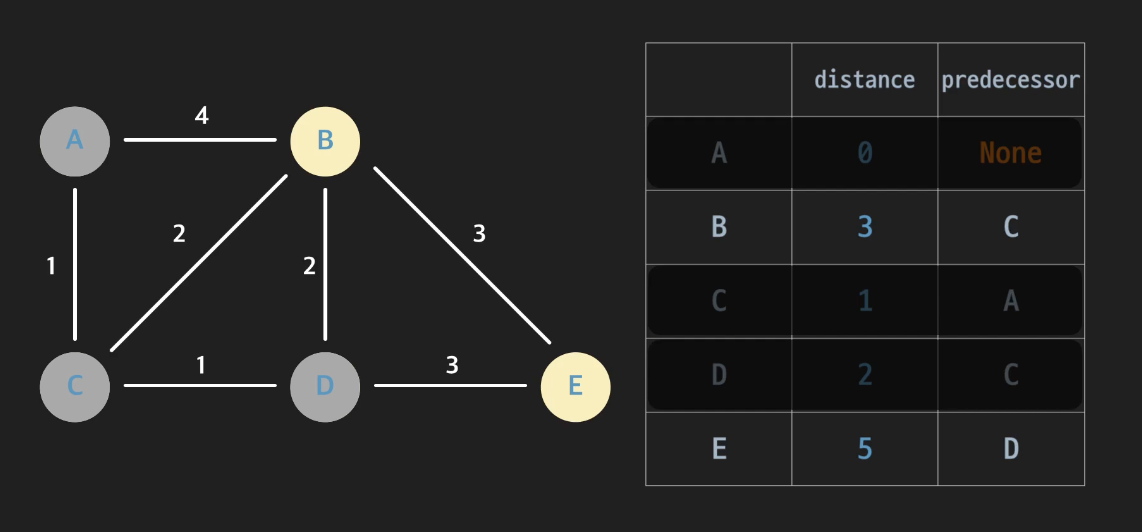
• 그 다음은 B노드,

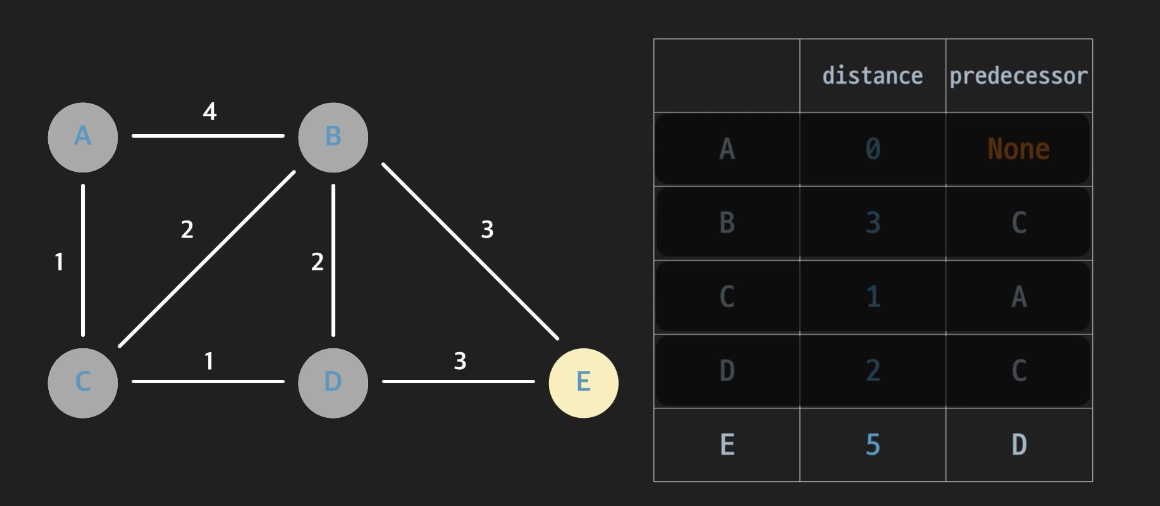
• 마지막으로 E노드까지 돌면 끝이다.
  

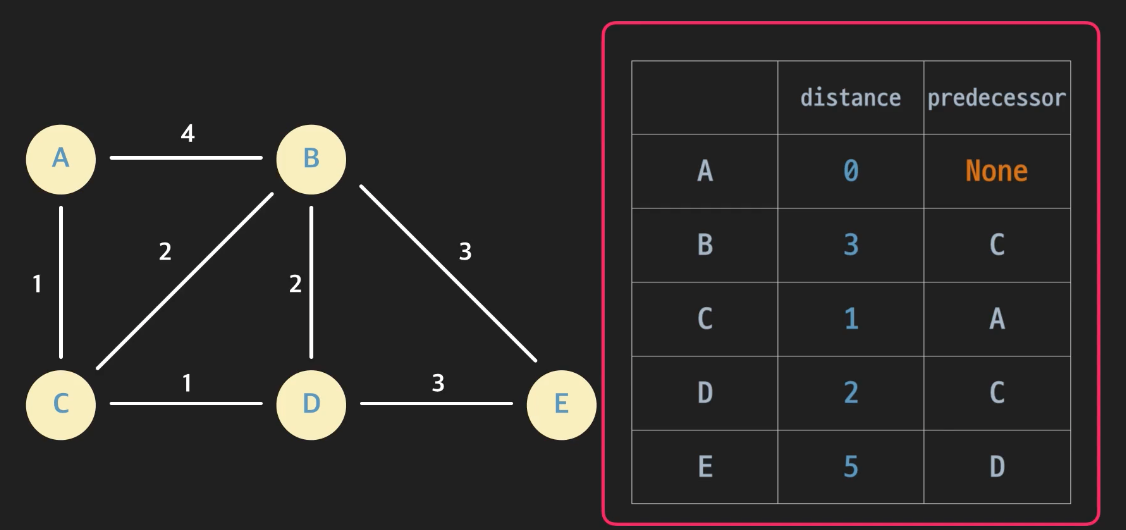
• 이렇게 마지막까지 돌면, 각 노드의 distance와 predecessor가 확정된다. 최단거리를 알고 싶으면, distance를 보면되고, 경로를 알고 싶으면 predecessor를 써서 Backtracking 을 사용하면 된다.

Dijkstra 알고리즘 수도코드
이를 일반화해서 정리하면 다음과 같다.

시작점의 distance를 0으로, predecessor를 None으로
모든 노드가 complete 일 때까지:
	complete하지 않은 노드 중 distance가 가장 작은 노드 선택
    이 노드에 인접한 노드 중 complete하지 않은 노드를 돌면서 :
    	각 엣지를 relax한다.
    현재 노드를 complete처리한다.