메타 휴리스틱
- [메타 휴리스틱] 1. 타부서치
- [메타 휴리스틱] 2. 시뮬레이티드 어닐링
- [메타 휴리스틱] 3. 유전자 알고리즘
다음 글은 경영과학에서 배우는 내용을 정리함.
0️⃣ 메타휴리스틱이란?
선형계획법, 동적계획법, 정수계획법, 비선형계획법은 최적해를 구하는 알고리즘에 집중한다. 그러나 최적해는 구하는 시간이 오래 걸리는 단점이 있다. 그래서 최적해를 포기하는 대신, 빠른 시간 내에 최적해와 가까운 해를 찾고자 했고, 이러한 접근법을 메타휴리스틱(Metahueristics)이라고 한다.
보통 휴리스틱은 문제의 특성에 맞춰 설계되므로 문제마다 매두 다르다.
이 중 메타휴리스틱은 특정 문제 집단에 범용으로 적용할 수 있는 일반적인 휴리스틱을 말한다.
- 실행 가능한 영역에서 탐색을 강화
- 지역최적해에서 탈출할 수 있는 전략 & 지역 개선 방법 사이의 상호작용 조율
- 자주 사용되는 메타 휴리스틱 방법
- Genetic Algorithm(GA)
- Tabu Search(TS)
- Ant Colony Optimization(ACO)
- Partical Swarm Optimization(PSO)
- Simulated Annealing(SA)
1️⃣ 지역탐색방법 👀
지역탐색방법(Local Search Procedure)이란, 현재해 x의 이웃해(neighborhood) 중에서 가장 좋은 해로 이동하는 방법이다.
- 가능해 집합 S가 연속 집합인 경우에 현재해 x의 이웃해 집합을 N(x)라고 하자.
- N(x)는 중심이 x이고 반지름이 인 구 와 S의 교집합에서 x를 뺸 집합이다.
- 가능해 집합 S가 이산 집합인 경우, 문제마다 N(x)를 정의하는 방법이 다르다.
<< Minimize 문제일 때 >>
a. 초기화 단계 : 초기해 x 선정
b. 반복 단계 : Local Search -> N(x)에서 제일 좋은 해 x'를 선택
c. 종료 단계 : Z(x) <= Z(x') 이면 x를 출력하고 종료. 그렇지 않으면 x=x'로 두고 반복단계 수행✔️ 🧳 🧭 🧑💼 외판원 문제
외판원 문제(Travelling Salesman Problem, TSP)는 외판원이 도시1을 출발해서 다른 도시를 각각 한 번씩만 방문하고 다시 도시1로 돌아오는 경로를 결정하는 문제이다.
목적
경로의 거리나 시간을 최소화하고 싶을 때
응용
택배배송 경로, 회로 기판 구멍 뚫는 문제
가능해 표현
1부터 n까지의 숫자로 이루어진 순열(단, 1이 항상 맨 앞과 끝에 있음)
가능해 수
도시의 개수가 n개일 때, (n-1)!/2 개이다. (모든 경우가 가능해이진 않다. 경로가 없을 수도 있으니까.)
- 아래와 같은 경로가 있다고 하자!
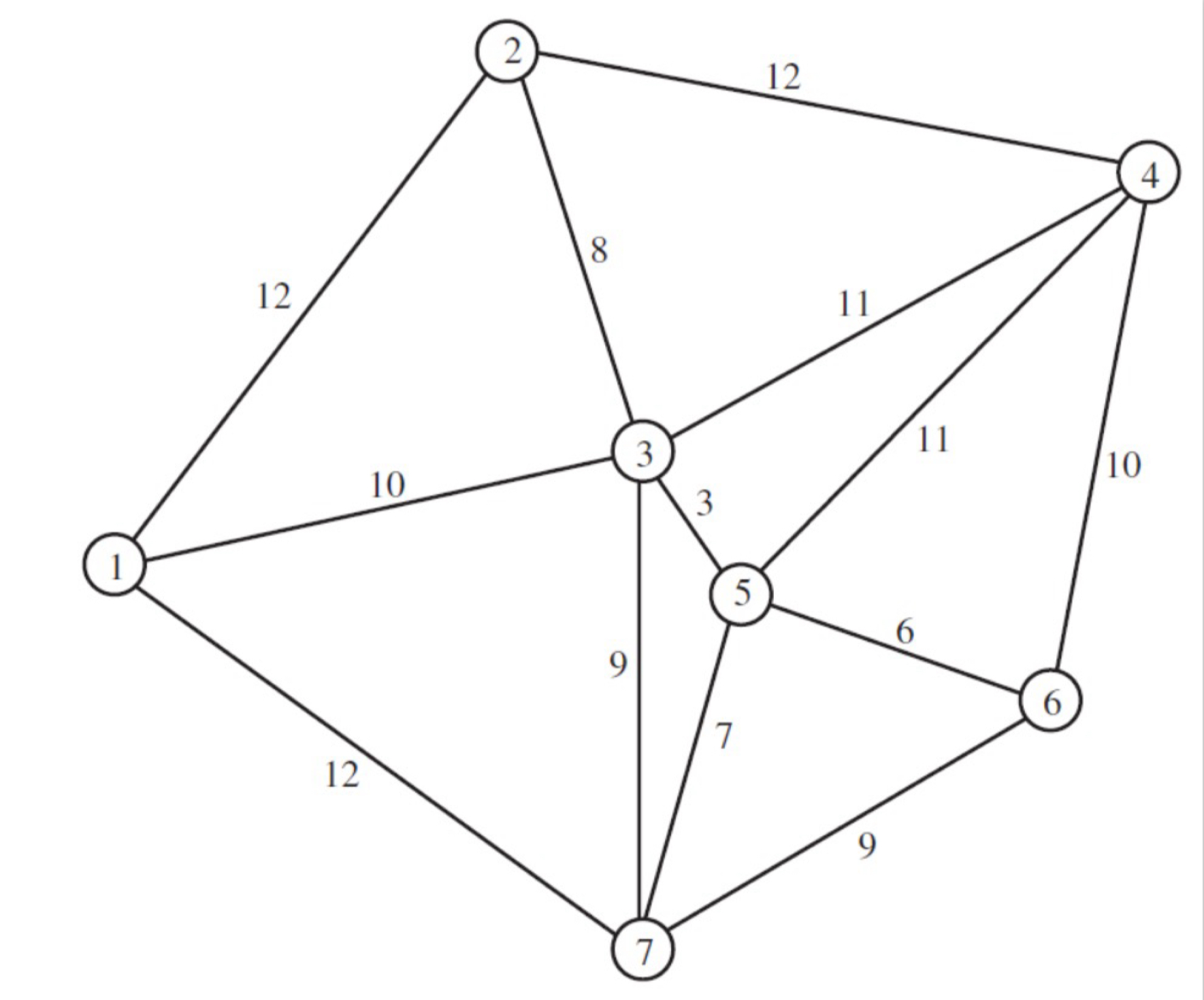
하위경로 역순 Neighborhood N(x)
현재해에서 이웃해는 어떻게 설정할까? 하위경로역순으로 이를 설정한다.
현재해의 방문할 도시에서 일부 구간의 순서를 거꾸로 해서 만들 수 있는 해의 집합을 의미한다.
하위경로역순의 시작점과 끝점을 랜덤하게 선택한다. 만약
1-2-3-4-5-6-7-1 에서 2-3-4-5 가 선택됐다면,
1-5-4-3-2-6-7-1 이렇게 그 부분을 뒤집으면 된다.
아래는 3-4 가 선택되었을 때다.
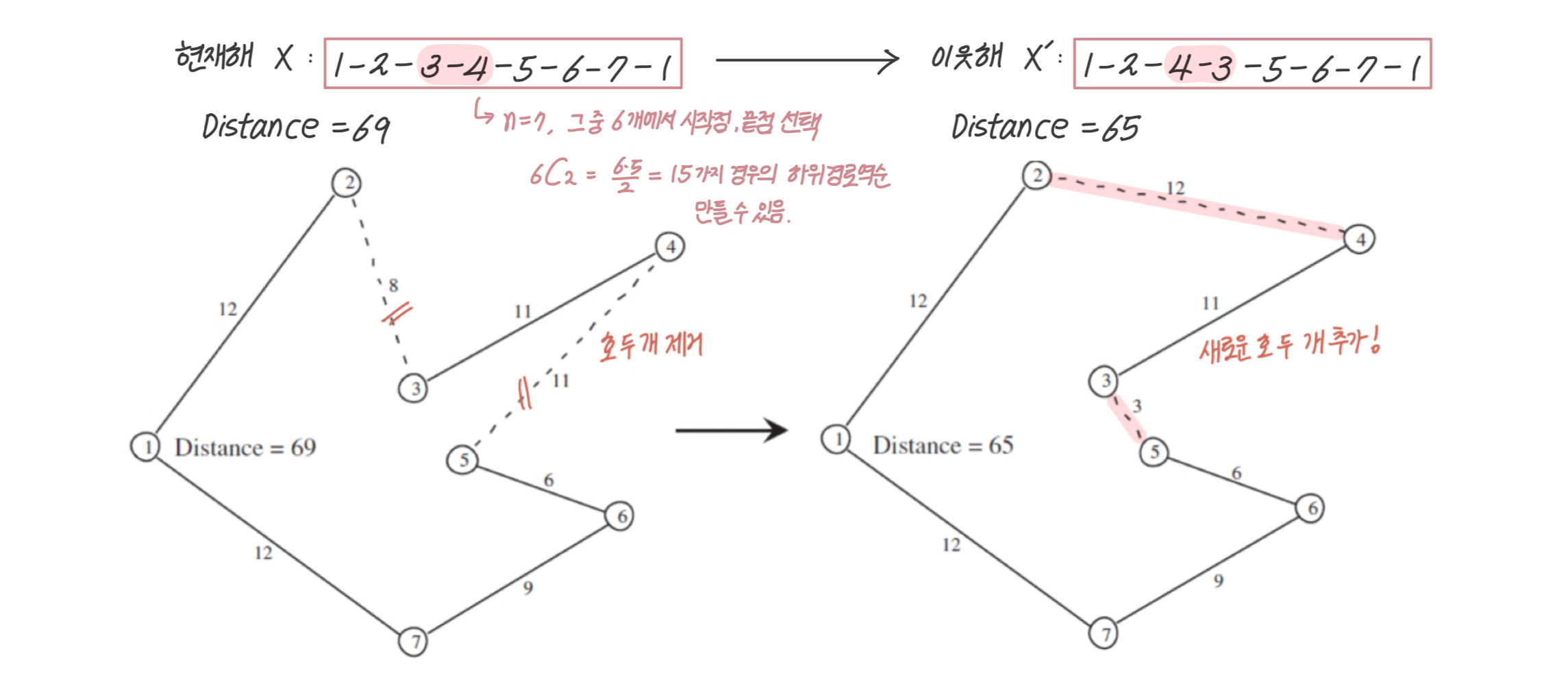
✔️ 하위경로역순 알고리즘
하위경로역순 Neighborhood를 이용한 Local Search 알고리즘이 어떻게 작동하는지 보자.
a. 초기화 : 초기해는 무작위로 실행가능한 경로를 선정한다.
b. 반복단계
1. 전체 경로의 역순을 제외하고, 가능한 모든 하위 경로 역순을 수행한다.
2. 거리가 가장 많이 감소한 경로를 새로운 해로 사용한다. (동률인 경우에는 임의로 선택)
c. 하위 경로 역순으로 더 이상 개선이 없으면 종료하고, 그 때의 해를 출력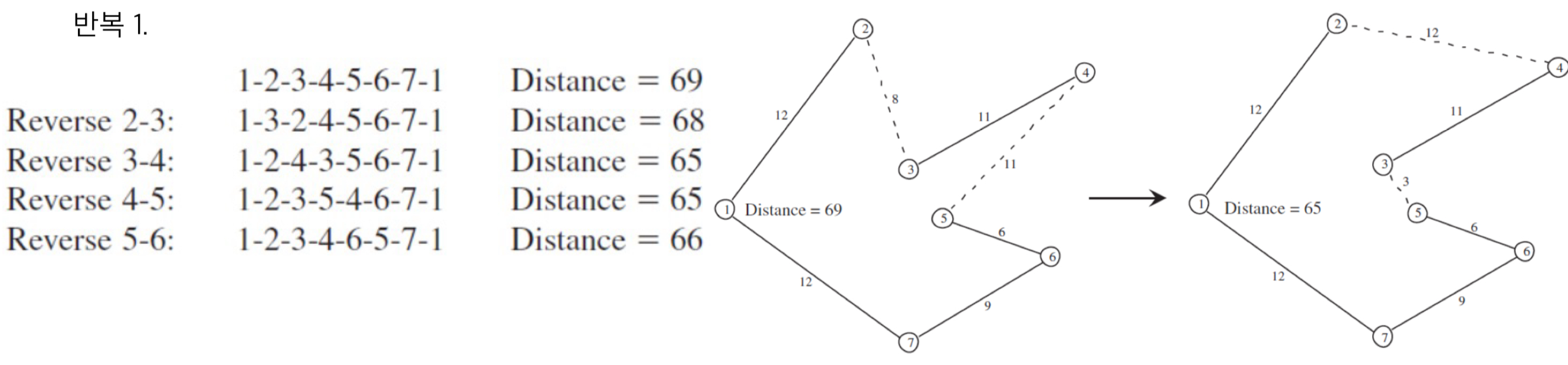
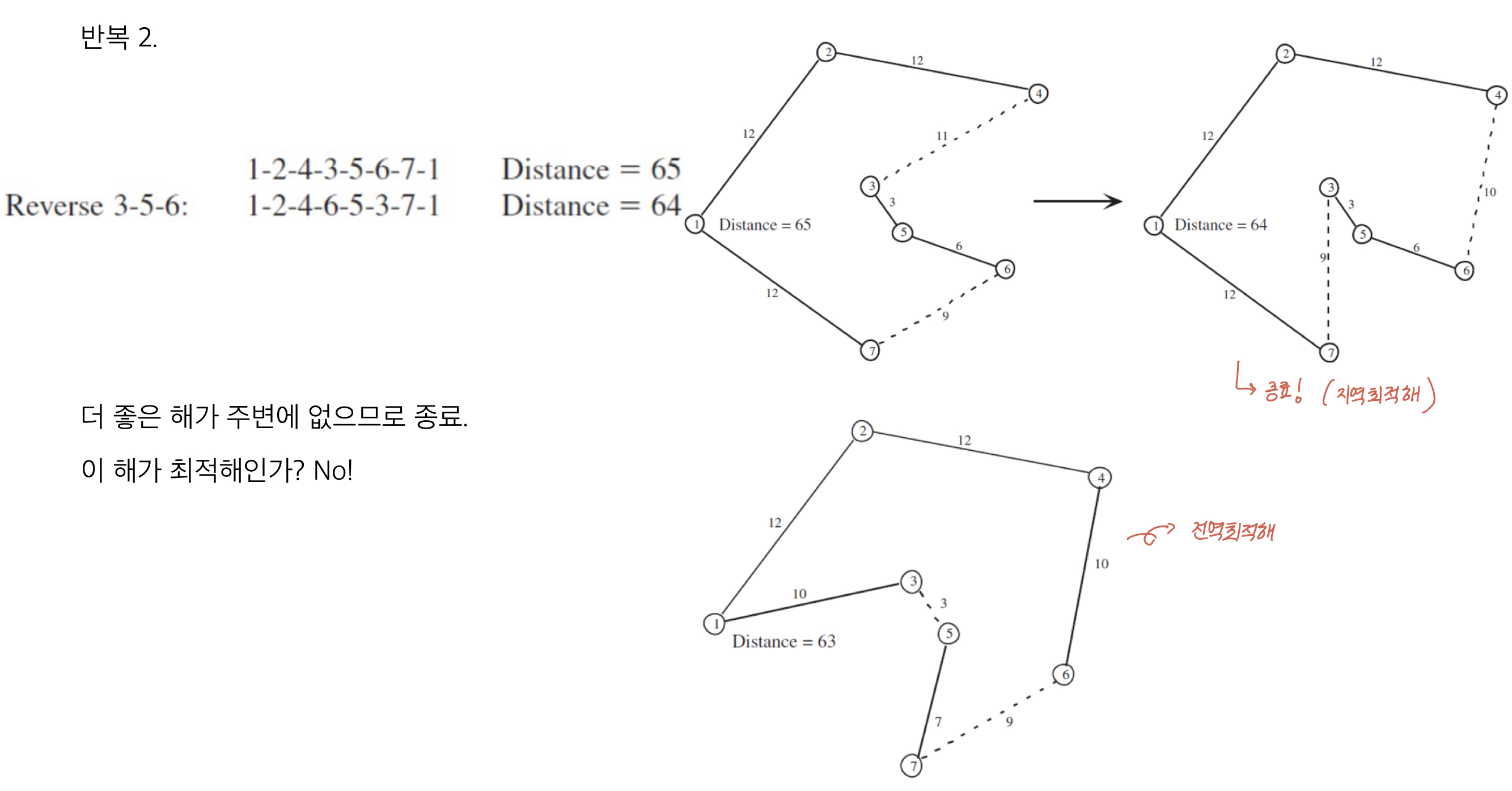
위 상황을 보면, Local Search로 해를 찾게 되면 더 좋은 해가 주변에 없으므로 종료하게 된다. 이 해는 지역최적해이고, 전역최적해는 아니다.
2️⃣ 타부서치
Local Search의 단점 : 지역최적해에 수렴해서 전역최적해를 못 찾는다.
이런 문제를 해결하기 위해 타부서치는 후보해가 현재해보다 목적함수보다 나쁘더라도 그 쪽으로 이동하는 것을 허용한다.
대신 같은 지역최적해를 순환할 수 있다는 단점을 막기 위해서 그쪽으로의 해 이동을 일시적으로 제한한다. 이렇게 갈 수 없는 이동을 타부 이동(Tabu move)라고 한다. Tabu는 독일어로 '금기'를 뜻한다. 그리고 이 타부 이동을 기억하는 공간을 T = Tabu list 라고 한다. 최근 탐색한 해를 타부 목록에 기록하는데, 이런 기억공간을 사용하는 것이 인공지능의 기본이 된다. Short Term Memory, Long Term Memory 이런 것이 타부리스트다.
✔️ 타부서치 알고리즘 과정
<<Minimize 문제>>
a. 초기화 : 초기해 x 선정. x* = x, Z* = Z(x)
b. 반복단계
1. Local Search : N(x)에서 타부상태가 아닌 제일 좋은 해 x'를 선택
2. IF x'의 타부 이동이 타부목록 T에 포함되면;
2-1. IF z(x') < z* 이면(목적함수가 개선되면);
x'의 타부이동을 타부목록 T에 추가하고 x=x'
3. Else ; x'의 타부이동을 타부목록 T에 추가하고 x=x'
4. IF z(x) < z*이면; x* = x, z* = z(x)
c. 종료단계 : 정해진 횟수나 시간이 지나거나 or 특정 조건 만족하면 종료
=> 종료할 때까지 가장 좋은 해 출력✔️ 타부서치 알고리즘에서 명확히 할 것
- 어떤 Local Search를 사용할 것인가?
- 이웃해 구조를 어떻게 정의할 것인가?
- 타부 목록에 기록하는 타부 이동을 어떤 형태로 표현할 것인가?
- 위 TSP예시 : [Tabu List] = (2-3), (4-7) 호를 끊을 수 없다.
- 각 반복마다 어떤 타부 이동을 타부목록에 추가시킬 것인가?
- 위 TSP예시 : 추가하는 두 호를 다음에 제거하는 호로 사용X
- 타부목록의 최대 크기는 얼마로 유지할 것인가? 타부목록은 FIFO(First In First Out)으로 유지한다.
- 종료조건은 어떻게 할 것인가?
3️⃣ 타부서치 예제
✔️ 1. 제약있는 최소걸침나무 예제
최소걸침나무 문제는 Greedy 알고리즘으로 O(nlogn)안에 풀린다.
- 최소걸침나무 문제에 다음과 같은 제약사항이 추가된 문제를
제약이 있는 최소걸침나무 문제라고 한다.- 제약1 : 호AD 는 호DE가 추가된 후에만 추가될 수 있다.
- 제약2 : 호 AB, AD, CD 중 많아야 하나만 추가될 수 있다.
제약이 있는 최소걸침나무 문제는 Greedy 알고리즘으로 풀 수 없다.- 제약을 어길 때 목적함수에 패널티를 부과한다.
- 제약 1을 어길 때 : 패널티 100
- 제약 2를 어길 때 : 호 AB, AD, CD 중 두 개가 포함되면 패널티 100, 3개가 포함되면 패널티 200
타부서치
1. Local Search
각 반복마다 타부상태에 있지 않다면, 현재해에서 이웃한 제일 좋은 해를 선택한다.
2. 이웃해 구조
호 하나를 추가시켜서 만들고, 이때 생긴 사이클에 포함된 호 하나를 제거해서 만들 수 있다. -> 이렇게 만든 해를 '이웃걸침나무해'
3. 타부이동의 형태
타부 목록에 있는 호는 사이클에 포함되더라도 제거하는 게 금지
4. 타부 이동의 추가
반복마다 걸침나무에 새롭게 추가되는 호를 타부 목록에 추가
(새롭게 추가된 호를 다음 Step에서 바로 제거하면 안 됨! 그럼 그 전 상태로 돌아가는 거니까! => 타부목록에 추가)
5. 타부 목록의 크기
2개 => 너무 많으면 해가 변경이 안 됨! (= 좋은 해 출력X)
6. 종료조건
3번 연속 현재 최적해를 갱신하지 못하면 종료
초기해는 제약이 없는 최소걸침나무 문제의 최적해를 사용
-
초기해 상태에서 모든 이웃해의 cost를 구한다. 호 DE가 추가되었다 할 때, 이를 Tabu list에 추가한다.
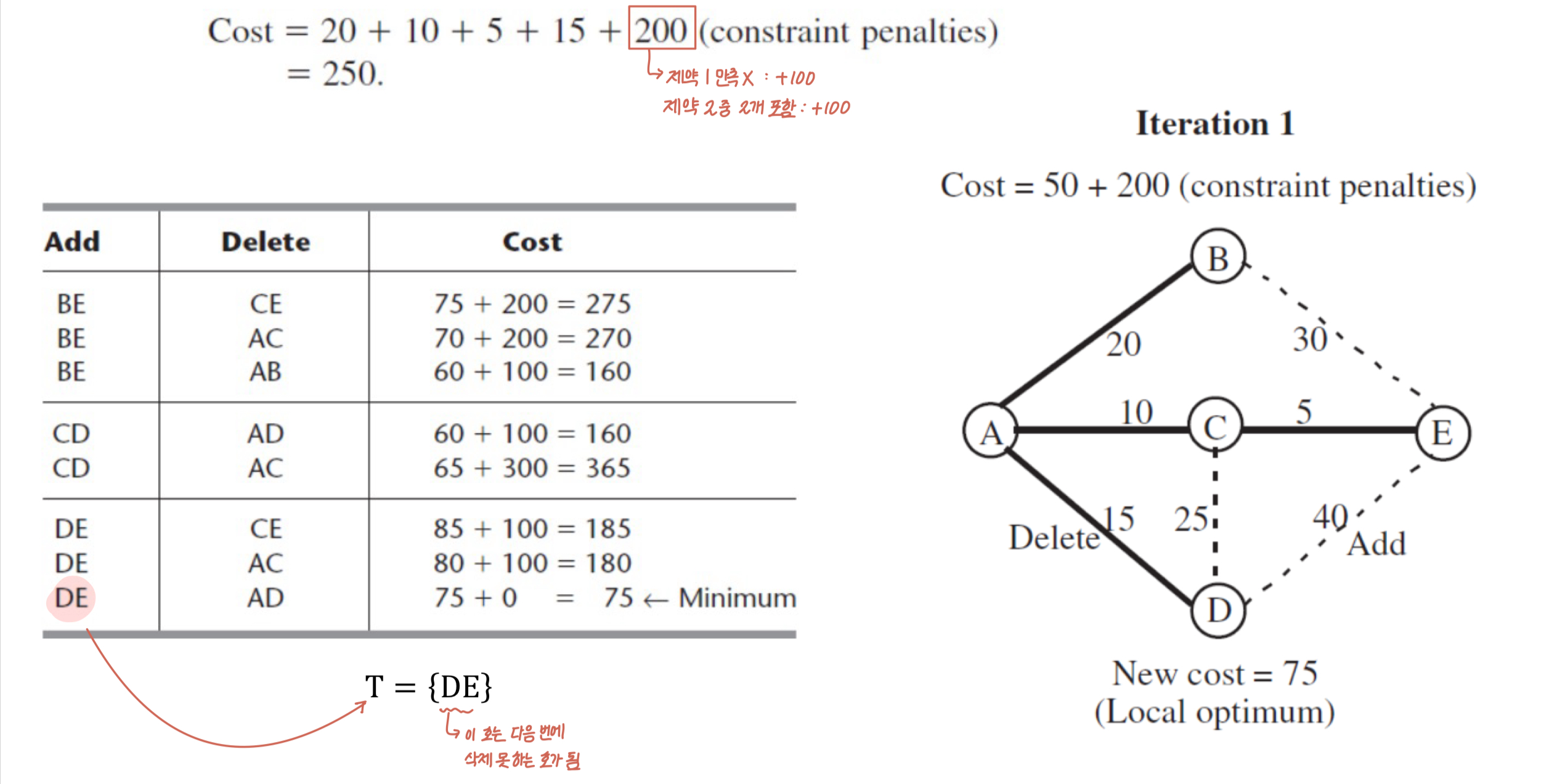
-
마찬가지로 또 가능한 모든 이웃해를 구하는데, AD가 추가되고 DE가 삭제하는 경우는 위의 상황으로 다시 되돌아가는 Tabu Move이므로 고려하지 않는다.
-
CD가 추가되고 DE가 삭제되는 상황일 때는 cost를 작성해주는데,
- 1) 전 상태로 돌아가지 않고,
- 2) 목적함수가 더 좋아지는 경우,
두 경우중 하나를 만족하면 cost를 작성한다.
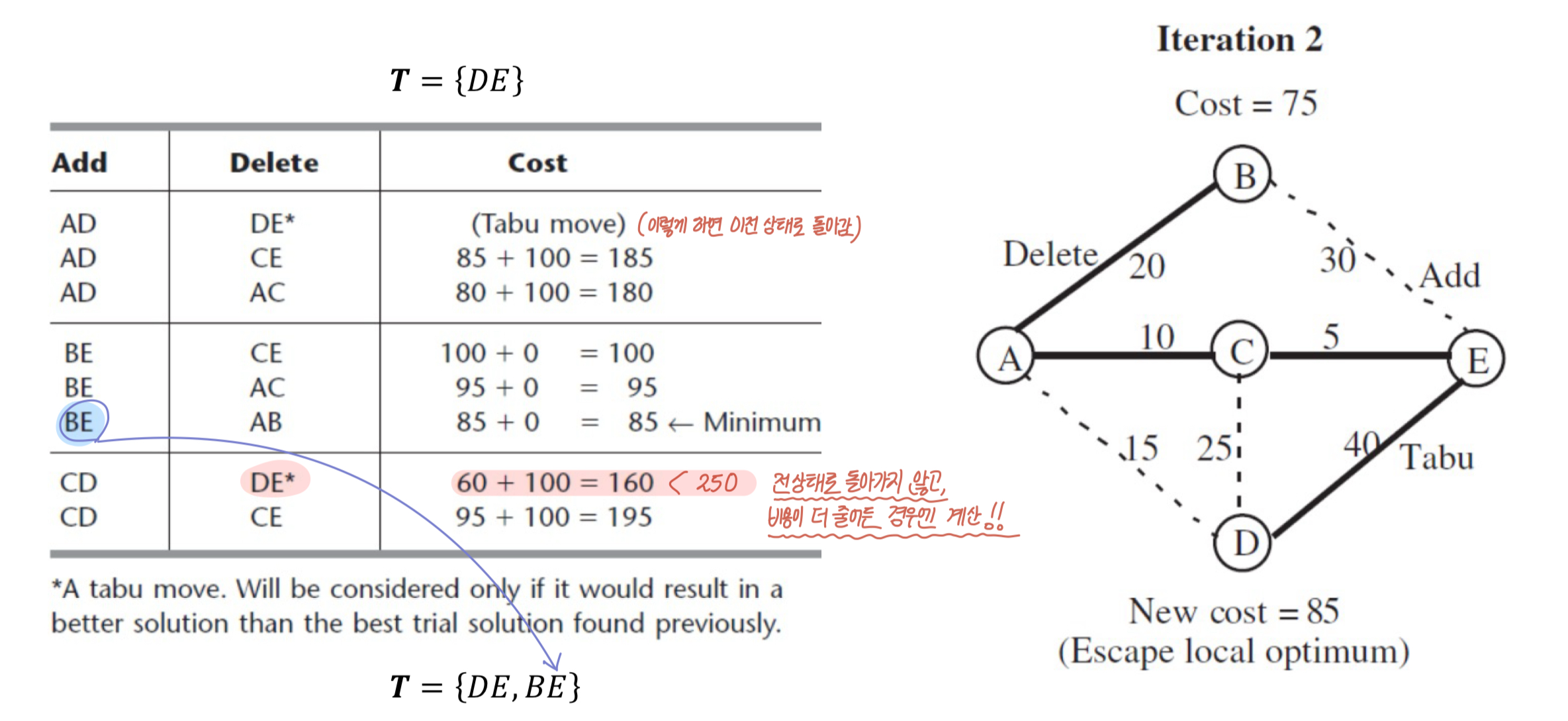
-
아래처럼 타부리스트에 있더라도 목적함수값이 개선되는 경우가 있음. 이런 경우에는 타부리스트 무시
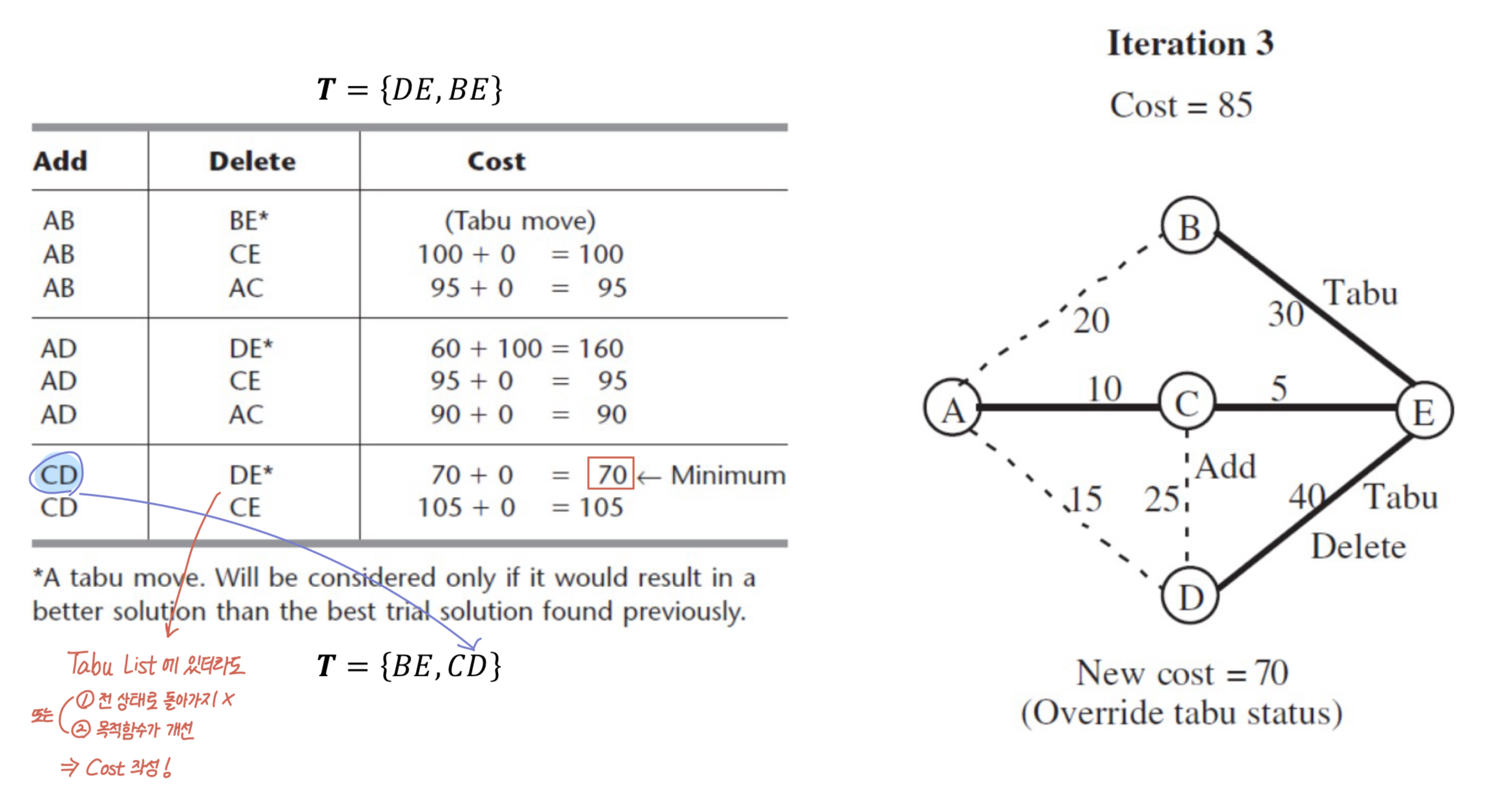
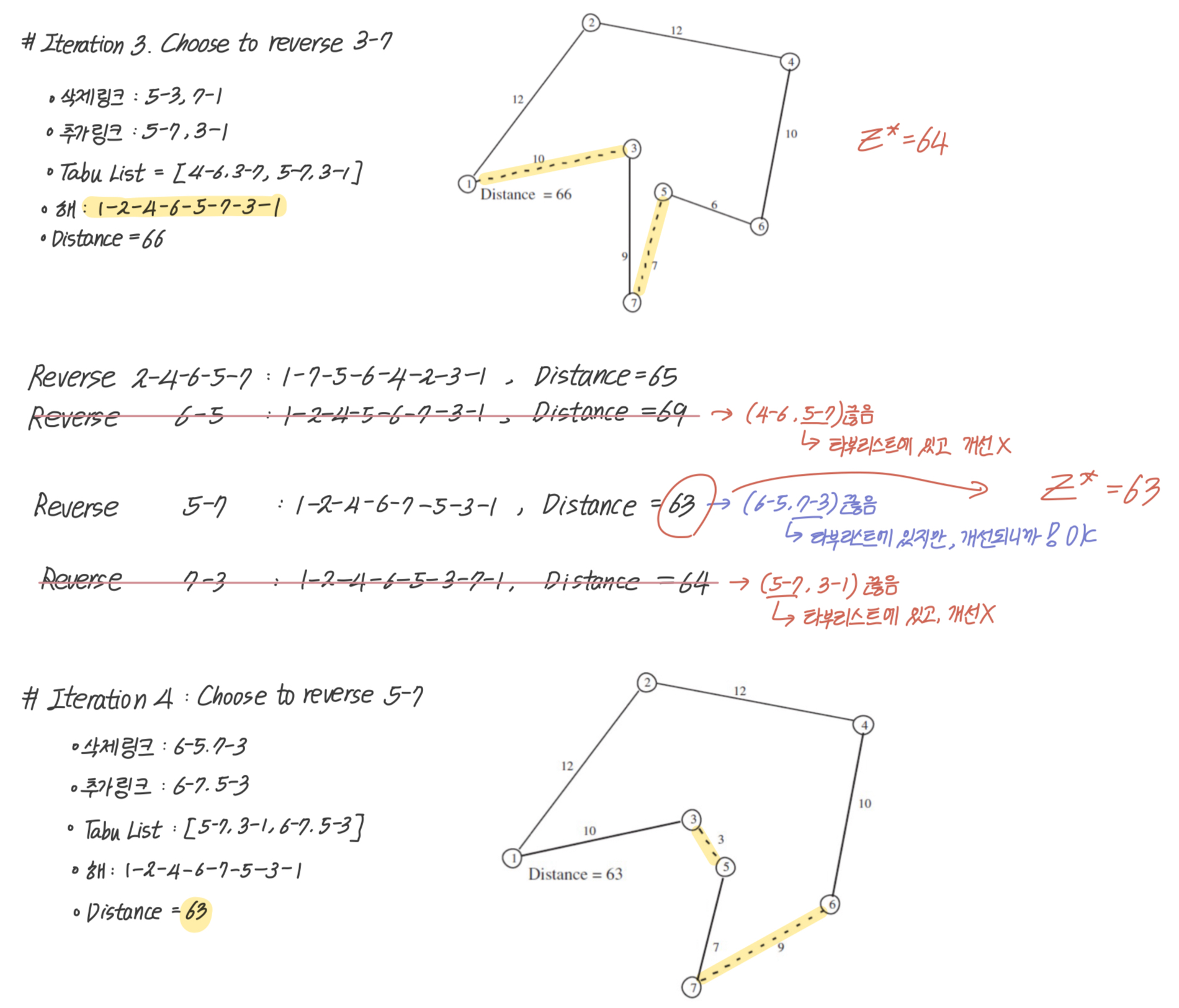
✔️ 2. 외판원 예제
Local Search
각 반복마다 타부상태에 있지 않다면, 현재해에서 이웃한 제일 좋은 해를 선택한다.
이웃해 구조
하위경로역순 Neighborhoods
타부이동의 형태
타부 목록에 있는 호는 앞으로 하위경로역순에서 제거 금지
타부이동의 추가
하위경로역순할 때 새롭게 추가된 두 호는 타부목록에도 추가
타부이동의 크기
4 (각 반복마다 2개의 호가 추가되므로 최소걸침나무문제의 타부목록 크기보다 2배)
종료조건
3번 연속 현재 최적해를 갱신하지 못하면 종료


메타휴리스틱 관련 글 보려고 들어왔다가, 좋은 글 많이 있어서 큰 도움 받고 갑니다~
감사합니다