다음 글은 경영과학에서 배우는 내용을 정리함.
0️⃣ 시뮬레이티드 어닐링
메타 휴리스틱은 대부분 자연현상을 관찰하여 만든 것이 많다.
시뮬레이티드 어닐링도 마찬가지로 '어닐링(Annealing)'을 모방했다. 어닐링은 어떤 물체의 열을 높여 분자의 자유도를 높였다가 열을 서서히 낮추면 분자 상태가 더욱 단단해지는 것을 이용한다.
문제에서는 현재해의 온도를 높여, 현재해 주변,
이전 게시글에서 소개한 '타부서치'는 가장 높은 언덕을 찾는 시간보다 각각의 언덕을 오르는 데에 시간을 많이 소모한다. 그러다보니 지역최적해에 너무 매몰되어 있을 수가 있다.

반면 시뮬레이티드 어닐링은 가장 높은 언덕(전역최적해)을 찾는 데에 중점을 둔다. 그러다보니 이웃해를 선택하는 방법이 타부서치랑 다르다.
✔️ 용어 정리
- : 현재해(current solution)의 목적함수 값
- : 후보해(next solution)의 목적함수 값
- : 온도로, 현재해보다 개선되지 않았지만, 후보해로 선택할 정도를 나타내는 파라미터.
- T가 높으면, 이더라도(후보해가 안 좋더라도), 후보해쪽으로 가능성이 높다.
✔️ 이동선택규칙(move selection rule)
후보해를 선택하는 규칙이다. 현재해에 인접한 이웃해 중, 다음해가 될 후보해()를 랜덤하게 선택한다.
- 최대화(Maximize) 문제인 경우
- 이면, 후보해를 다음해로 선택
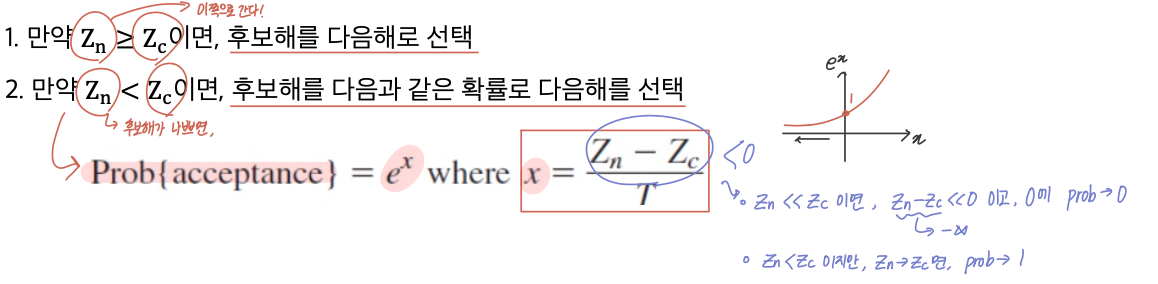
- 이면, 아래와 같은 확률로 다음해를 선택
이면 즉, 후보해인 Zn이 현재해보다 많이 작으면 확률은 거의 0이 되어 선택되지 않는다. 반면에 차이가 작다면, 확률은 거의 1이 된다.
- 최소화(Minimize) 문제인 경우
- 위와 완전히 반대로, Zn과 Zc의 위치를 바꾸면 됨
- 위와 완전히 반대로, Zn과 Zc의 위치를 바꾸면 됨
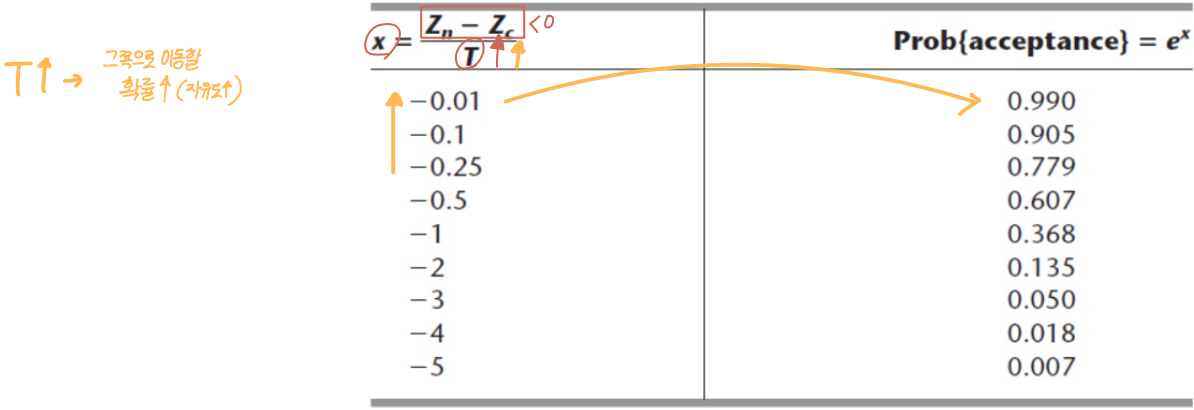
- 여기에서 (온도)가 크다는 것은, 가 동일할 때 다음해로 선택될 확률이 더 커진다는 것이다.
✔️ 이동선택규칙의 특징
- 위 식을 보면, 약간 낮은 아래쪽 언덕으로 이동하는 것은 허용하나, 가파른 아래쪽 언덕으로 움직이는 확률은 작다.
- T값은 상대적으로 큰 값으로 시작한다. 처음에 후보해 선택 확률을 크게 하여 많은 곳을 탐색할 수 있도록 하기 위함이다.
- 탐색과정에서 T를 점점 감소시킨다. 그럼 후보해 선택 확률이 줄어들어 위쪽으로 올라가게 된다.
- T값에 따라 반복횟수가 결정되므로, 알고리즘 성능에 많은 영향을 준다.
- 사전실험으로 파라미터를 선택한다. 문제마다 T의 상태에 따라 결과가 달라진다.
✔️ 시뮬레이티드 어닐링 알고리즘 과정
a. 초기화 : 실행가능한 초기해 선정
b. 반복단계 : 이동선택규칙을 이용하여 다음해를 선택한다.
단, 현재해에 이웃해가 없을 경우 알고리즘을 종료.
c. 온도표 확인 : 현재의 온도 T에서 정해진 반복횟수만큼 알고리즘을 수행.
온도표에서 다음 T값으로 감소시키고 다시 반복횟수만큼 알고리즘 수행
d. 종료단계 : 온도표에서 T값이 가장 낮아지거나, 더이상 현재해에 인접한 이웃해를 선택할 수 없으면 종료
지금까지 찾은 해 중 가장 좋은 해를 출력✔️ 시뮬레이티드 어닐링에서 명확히 해야 할 것
- 초기해를 어떻게 선택할 것인가?
- 현재해에 인접한 이웃해 구조를 어떻게 정의할 것인가?
- 현재해에 인접한 이웃해 중에서 다음의 초기해로 사용할 후보해를 선택하는 이동선택규칙의 랜덤성은 어떻게 할 것인가?
- 적절한 온도표는 무엇인가?
1️⃣ 시뮬레이티드 어닐링 예제
✔️ 1. 외판원 문제
1. 초기해
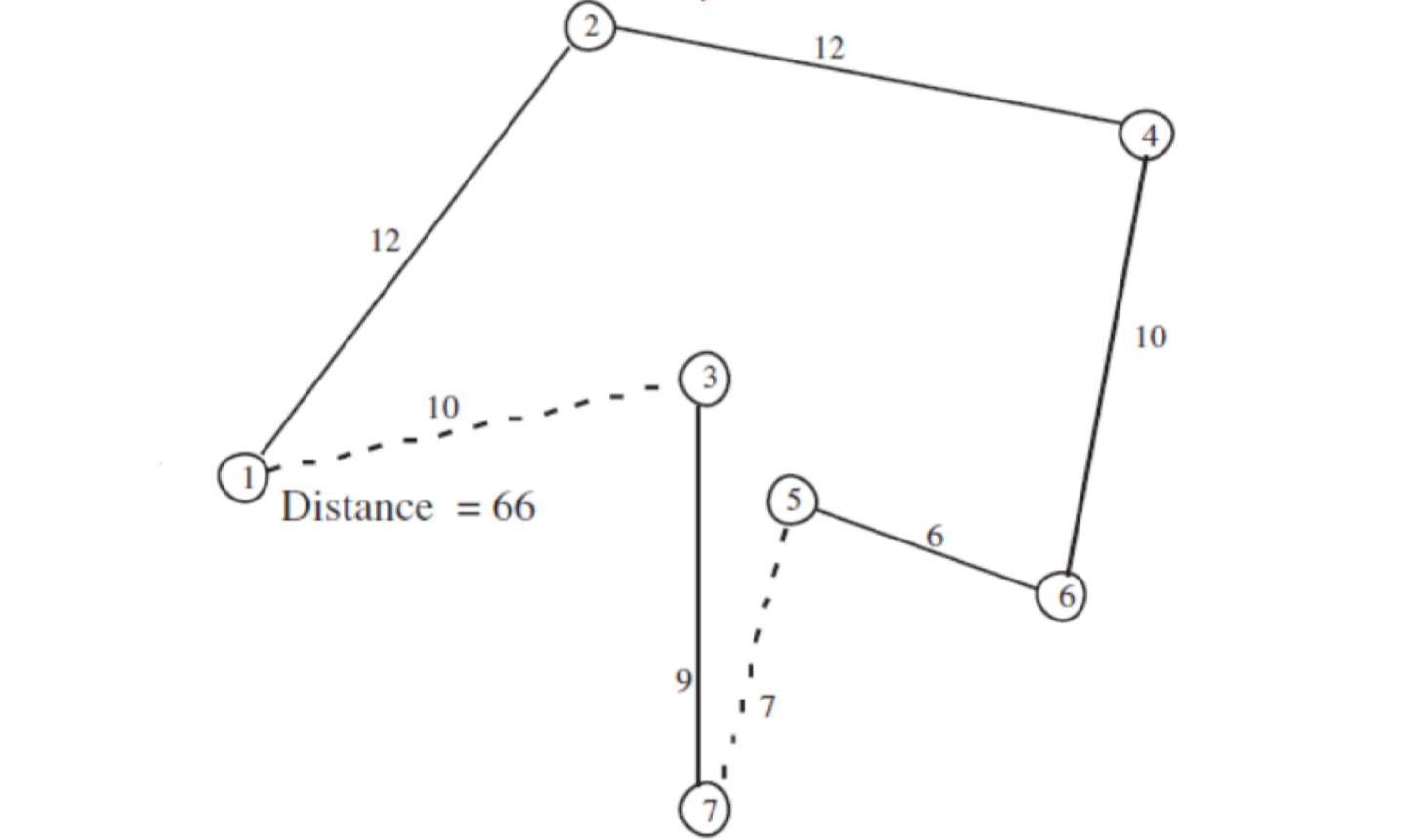
랜덤으로 발생시킬 수 있음 1-2-3-4-5-6-7-1
2. 이웃해 구조
하위경로역순 Neighborhood 1-2-6-5-4-3-7-1
3. 인접한 이웃해의 랜덤 선택
하위경로의 처음과 끝을 나타내는 구간을 선택해야 한다. 이 처음과 끝을 랜덤하게 선택
4. 온도표
5개의 T값에 대해 다섯 번의 반복 수행.
현재해의 목적함수 값이 Zc일 때,
T1 = 0.2Zc,
T2 = 0.5T1,
T3 = 0.5T2,
T4 = 0.5T3,
T5= 0.5T4 로 정의
여기에서 T1 = 0.2Zc는 일반적으로 |Zn - Zc|보다 T1값을 더 크게 하기 위한 식이다.
이렇게 최초 온도값인 T1 값을 크게 줘서 자유도를 높게 한다. 대규모 문제를 풀 때에는 각각의 T에서 더 많은 반복횟수를 사용하고, 온도표에서 T를 천천히 감소시킨다.
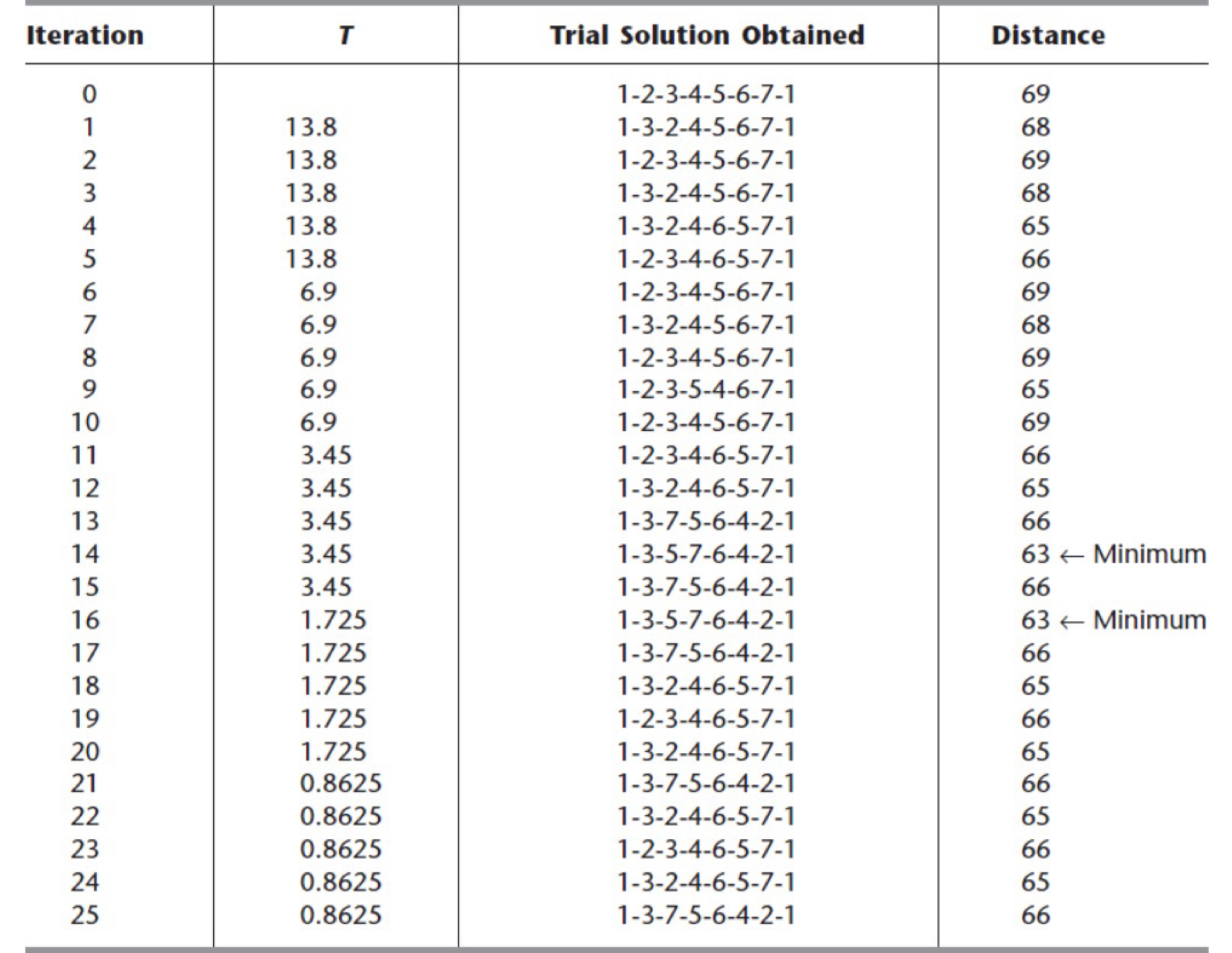
Iteration 1
Step1 하위경로역순의 시작 값을 랜덤하게 선택
1-2-3-4-5-6-7-1에서 시작값으로 선택될 수 있는 건 2,3,4,5,6 중 하나. 이 중 동일한 확률로 랜덤하게 하나를 선택한다.- 여기에서 3이 선택됐다고 가정한다.
Step2 하위경로역순의 끝 값을 랜덤하게 선택
- 시작 값(3) 뒤에 있는 숫자중(4,5,6,7) 하나를 랜덤하게 고른다.
- 여기에서는 4가 선택됐다고 하자.
- 그럼 3-4 사이 역순 경로인
1-2-4-3-5-6-7-1이 후보해가 된다.
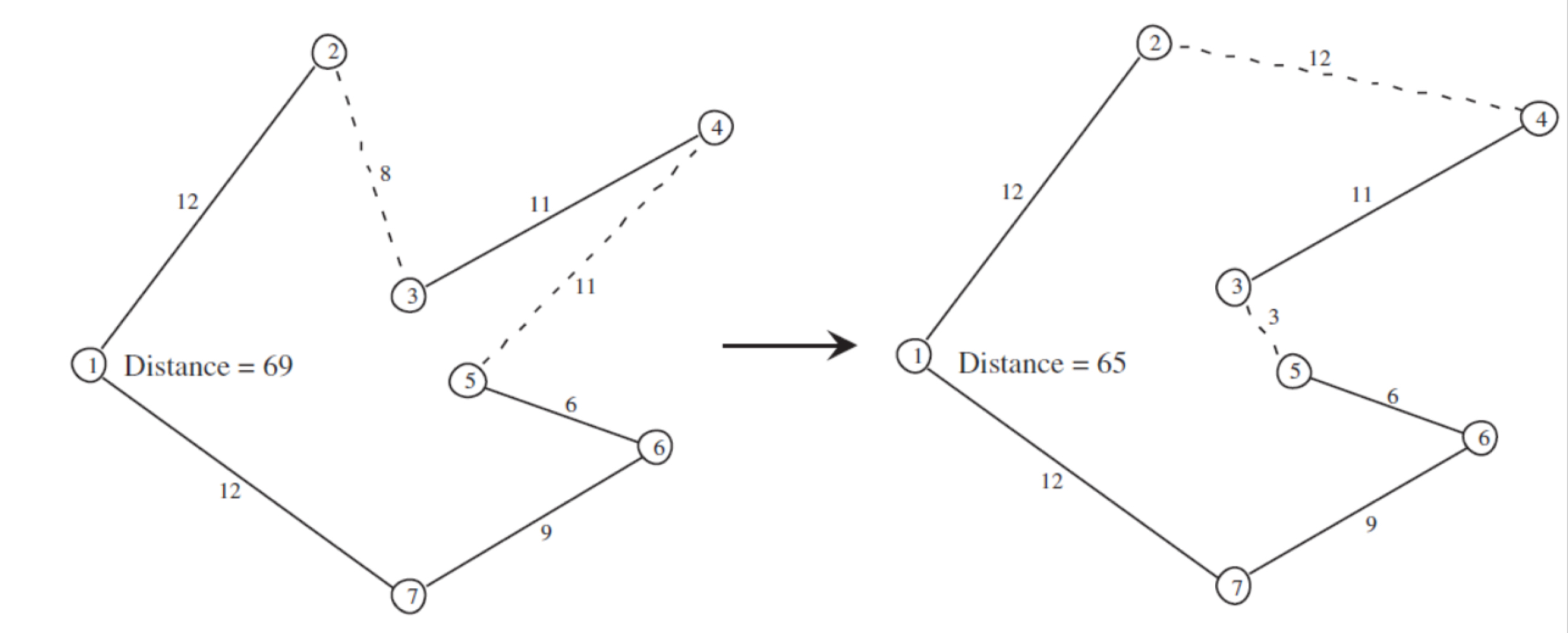
Step3 Zn 과 Zc 비교, 다음해 선택
- Zc(현재) :
1-2-3-4-5-6-7-1경로일 때, Zc = 69 - Zn(다음) :
1-2-4-3-5-6-7-1경로일 때, Zn = 65 - Zn < Zc 이므로, 목적함수가 더 좋아졌다. 이 후보해는 자동적으로 다음해로 선택된다!
Iteration 2
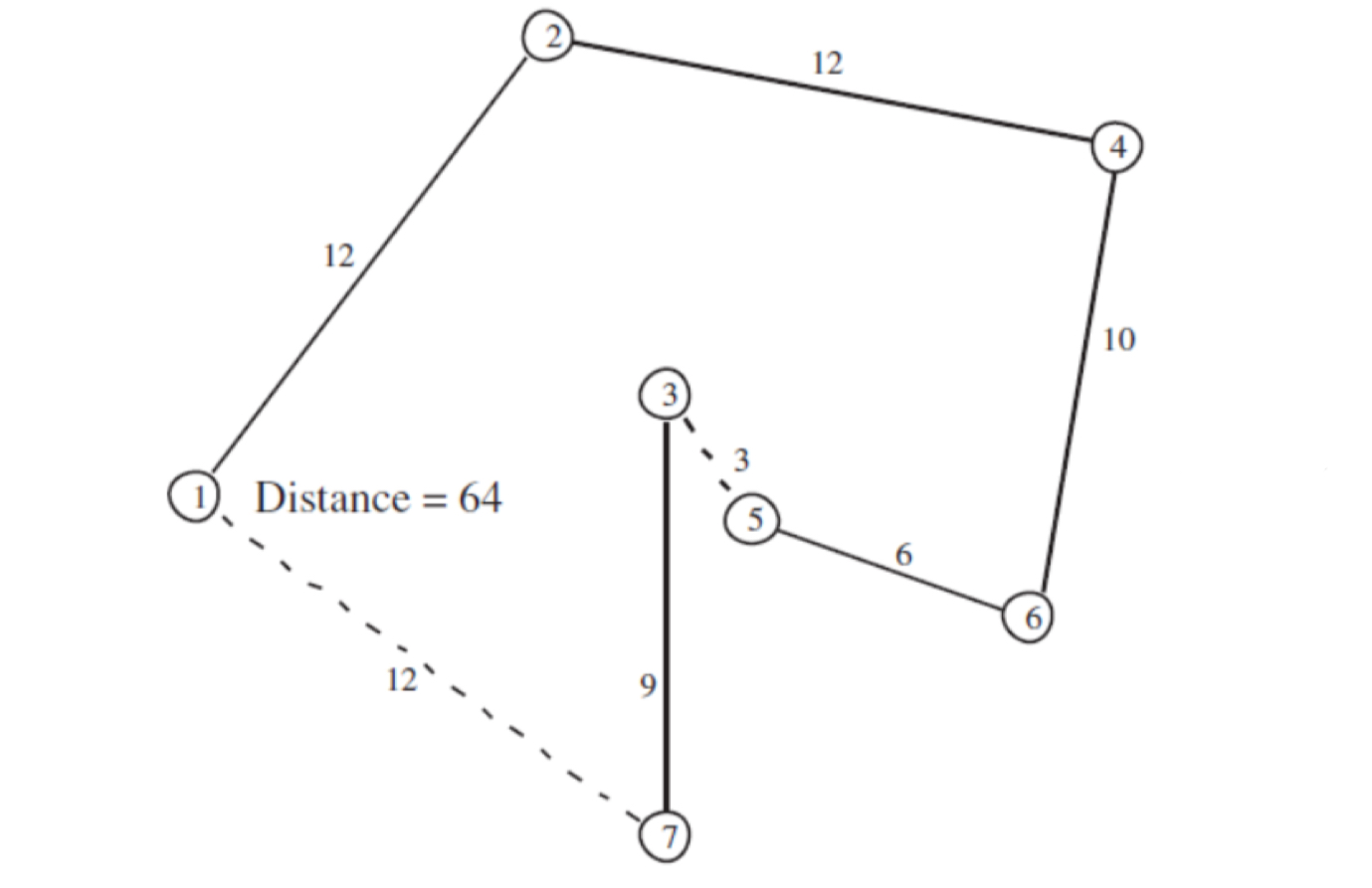
Step1-2-3 하위경로역순 선택후, Zn 비교
1-2-4-3-5-6-7-1에서 3-5-6 부분이 선택됐다고 했을 때, 후보해는1-2-4-6-5-3-7-1가 된다.- 이때 Zn = 64로, Zn(64) < Zc(65)이므로 목적함수가 더 좋아졌다. 이 후보해를 다음해로 선택한다.
Iteration 3 목적함수가 나빠졌을 때
Step1-2-3 하위경로역순 선택후, Zn 비교
1-2-4-6-5-3-7-1에서 3-7 부분이 선택됐다고 했을 때, 후보해는1-2-4-6-5-7-3-1가 된다.- 이때 Zn = 66로, Zn(66) > Zc(65)이므로 목적함수가 더 나빠졌다.
- 목적함수가 나빠졌을 때는 확률적으로 그쪽으로 갈 것인지를 정한다.
- T1 = 13.8
- Prob{acceptance} = 의 확률로 이 해를 선택한다.
- 이런식으로 목적함수가 나빠진 경우, 확률적으로 선택하게 된다. T는 목적함수가 나빠지지 않더라도 iteration마다 하나씩 소모하게 된다.
✔️ 2. 비선형계획 문제
아래 비선형계획 문제를 시뮬레이티드 어닐링으로 풀어보자.
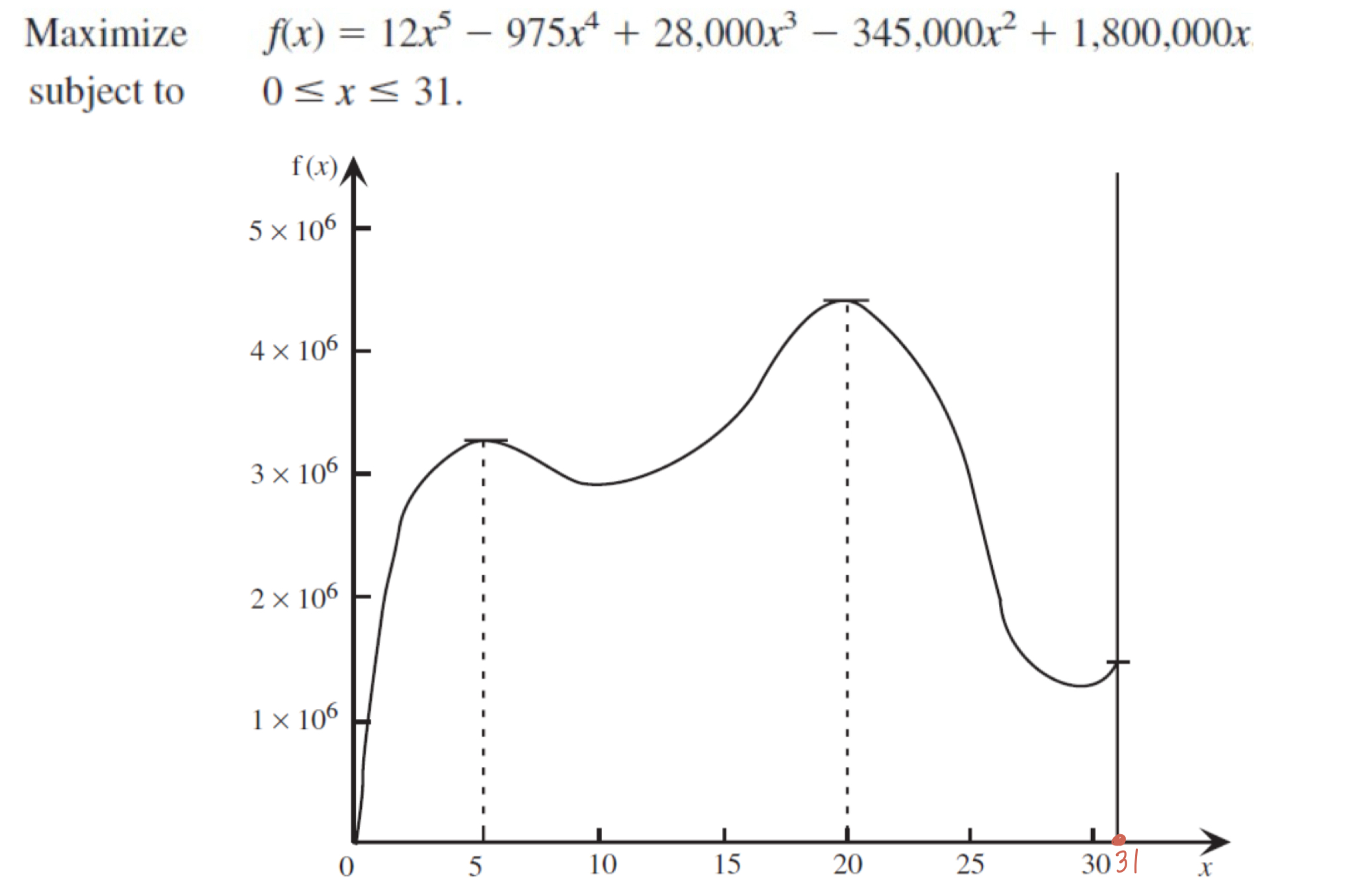
(하한), (상한)으로 설정하고 시작한다.
1. 초기해
으로 설정한다. 여기에서는 x = 15.5 이다.
2. 이웃해 구조
실행가능해 모두를 인접한 이웃해로 설정한다.
3. 인접한 이웃해의 랜덤 선택
표준편차와 현재해의 갱신은 아래와 같다.
만약 실행불가능해가 나오면 이 과정을 반복한다.
4. 온도표 : 5개의 T값에 대해 다섯 번의 반복 수행. 현재해의 목적함수 값이 Zc일 때,
T1 = 0.2Zc,
T2 = 0.5T1,
T3 = 0.5T2,
T4 = 0.5T3,
T5 = 0.5T4로 정의
여기서 으로 한 이유는 U와 L의 중간 값으로 xj가 있을 때, 새로운 값은 현재값의 표준편차 3 안에 있기 때문.
Iteration 1
-
초기값인 x = 15.5 부터 시작.
Zc = f(15.5) = 3,741,121 이고
T1 = 0.2Zc = 784,224
-
이제 N(0, 5.167)에서 랜덤으로 발생시킨다.
- [0,1]에서 난수를 생성한다. 예를 들어 0.0735가 생성되었다고 하자.
- N(0,1)에서 인
- N(0, 5.167) 에서 인
- x = 15.5 + N(0, 5.167) = 15.5 - 7.5 = 8
- Zn = f(8) = 3,055,616 < Zc (목적함수 값 나빠짐)
- prob{acceptance} = 의 확률로 다음해로 선택한다.
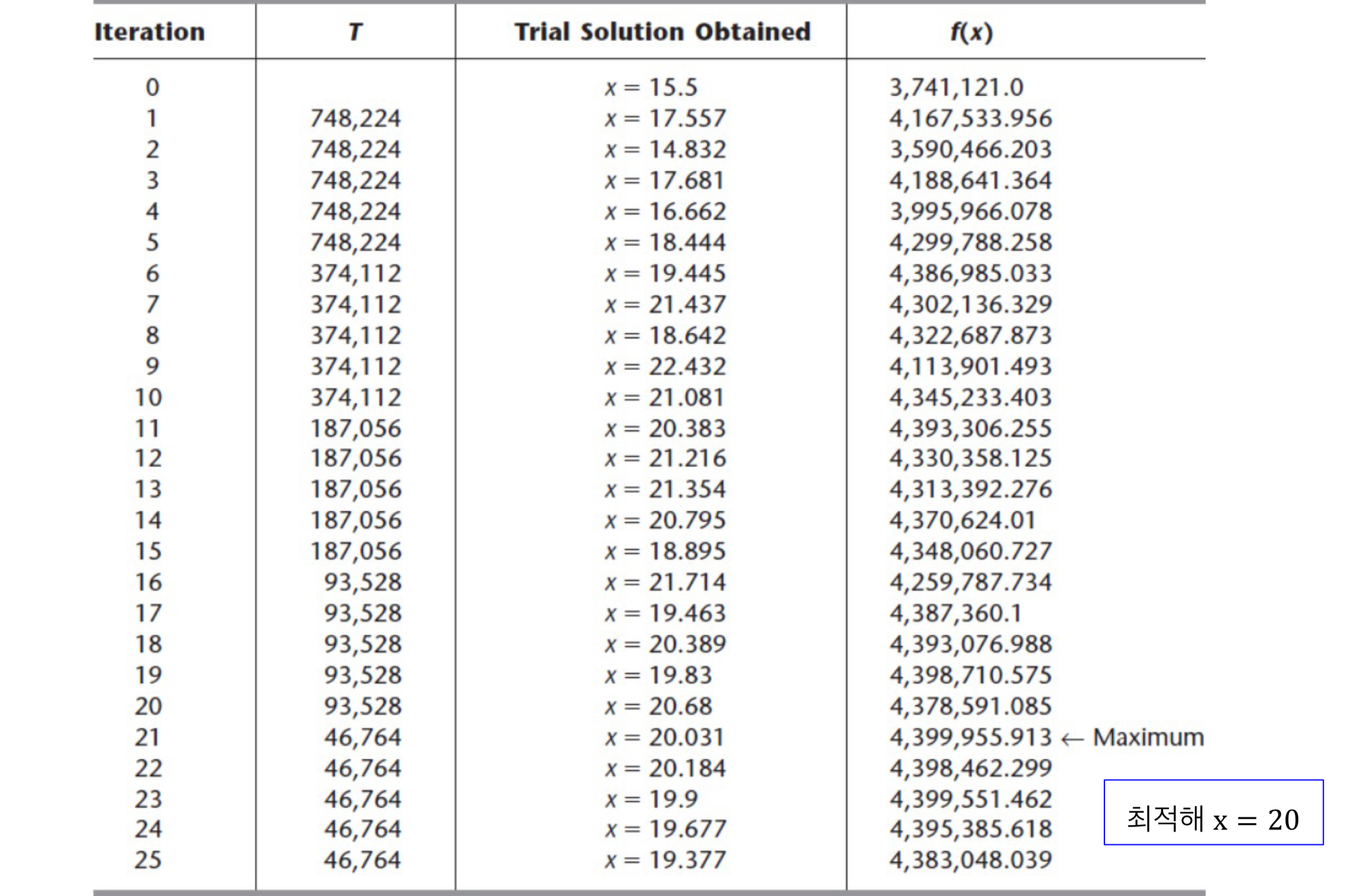
✔️ 3. 수도쿠(Sudoku) 문제
비용 정의
로 정의한다.
- 는 행 i에서 겹치는 숫자 쌍의 수
- 는 열 i에서 겹치는 숫자 쌍의 수
1. 초기해
각 블록에 숫자가 겹치지 않도록 랜덤하게 생성한다.
2. 이웃해 구조
블록 내에서 고정되지 않은 숫자 2개의 위치를 바꿔서 만들 수 있는 해
3. 인접한 이웃해의 랜덤 선택
블록 내에서 고정되지 않은 숫자 2를 랜덤하게 선택
4. 온도표
각 T값에 대해 빈칸 수만큼 반복을 수행
T1 = 가능해 200개의 비용의 표준편차,
이 영상에서 파이썬 코드로 구현하는 것도 나온다.Simulated Annealing Explained By Solving Sudoku - Artificial Intelligence 유투브

시뮬레이티드 어닐링 검색했는데 아무리봐도 제 전공 교재랑 같아서 놀랐는데 동기였네요;; ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ