[자료구조] 배열 접근/탐색, 정적배열, 동적배열

파이썬의 리스트와 C의 배열에는 차이가 있다.

• 파이썬 리스트
  • 계속해서 요소 추가 가능
  • 여러 타입의 요소 가능
• C 배열
  • 크기가 고정
  • 각 요소를 수정할 순 있지만 삭제는 불가능
  • 같은 타입의 데이터만 담을 수 있음

C 배열 : int numArray[4];
C배열은 크기를 정해놓고 시작한다. 메모리에 필요한 만큼의 공간을 미리 할당해 놓는다. 배열이 셀 공간을 미리 예약하는 거라고 볼 수 있다. C에서 정수 하나가 보통 4바이트이기 때문에 정수 4개를 담기 위해서 총 16바이트의 연속적인 메모리 칸을 예약한다.
numArray[0] = 2; 0번 인덱스에 정수 2,
numArray[1] = 3; 1번 인덱스에 정수 3 ...
이런식으로 예약한 16칸의 메모리중 각각 4칸씩 차지하며 저장할 수 있다.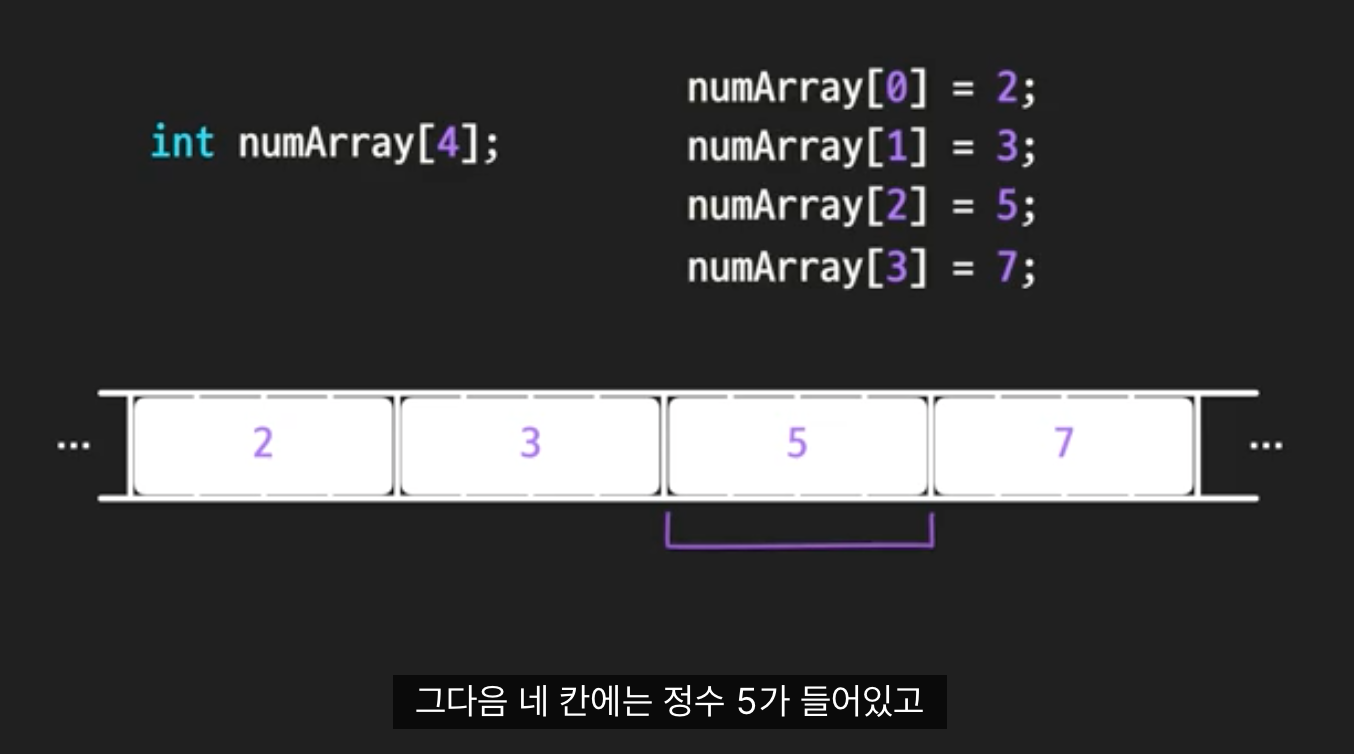

파이썬 리스트 : num_list = [2, 3, 5, 7]
파이썬 리스트는 요소들이 메모리의 연속될 필요없이 다른 곳에 저장될 수 있다. 메모리에는 실제 2, 3, 5,7에 대한 레퍼런스가 저장되어 있다. 그 메모리칸은 2,3,5,7을 가지고 있는 게 아니라, 이것을 가리키고 있다는 표현이 더 적절하다.

값들을 직접 가지고 있는 게 아니고, 가리키기 때문에 리스트의 길이가 길어져도 상관없고, 여러 타입의 데이터를 저장할 수 있는 것이다.

배열 접근/저장

배열에 데이터를 저장하고 가지고 오는 방법을 살펴보자. C언어를 기준으로 살펴보자.

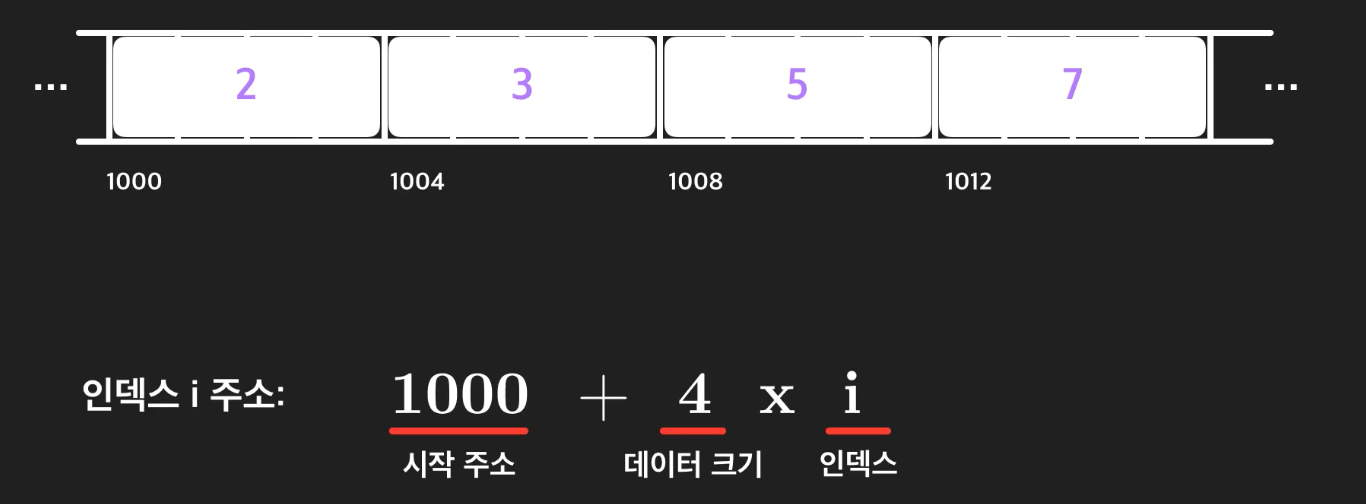
배열에 어떤 인덱스 값을 받아오기 위해서 그 값의 주소를 알아야 한다. 그 구조는 위처럼 간단한 계산으로 구할 수 있다. 그리고 주소를 알면 O(1)로 접근이 가능하다. 어떤 인덱스든 접근하는 데 O(1)밖에 안 걸리니 굉장히 효율적이라 할 수 있다. 배열은 주소만 정확히 알고 있으면 한 번에 접근할 수 있는 램의 특성을 잘 이용하는 자료구조다.

배열 탐색

접근은 인덱스를 통해 값을 찾는 거고, 탐색은 특정 조건을 만족하는 값을 찾는 것이다. 따라서 배열에서 탐색은 접근보다 비효율적이다. 어떤 값이 있는지 확인하기 위해서 첫 번째 인덱스에서 쭉 찾아가는 걸 선형탐색이라고 한다. 배열이 정렬되어 있지 않는 이상, 이 방법보다 효율적으로 탐색하긴 어렵다.

배열탐색의 효율성을 시간 복잡도로 나타내보자. 내가 찾고자 하는 값을 바로 첫 번째 인덱스에서 찾을 수도 있고, 배열에 값이 아예 없는 경우가 최악의 경우라 할 수 있다. 따라서 배열에 저장한 데이터가 n개일 때, 탐색에 걸리는 시간은 n에 비례한다. 시간 복잡도로 표현하면 O(n)이 걸린다.

정적 배열(Static Array)

배열은 정적배열과 동적배열이 있다. 일반적으로 배열을 말하면, 정적배열을 얘기한다.

• 정적배열 : 크기 고정 (요소 수 제한, ex.C배열)
• 동적배열 : 크기 변함 (요소 계속 추가 가능)

정적배열에선, 처음부터 어떤 타입의 데이터인지, 몇 개의 데이터를 저장할지를 정한다. 그리고 정수 5개를 담을 수 있는 배열에 요소가 꽉 차면 더이상 값을 추가할 수 없다. 그래도 그 배열에 꼭 하나의 요소를 추가하고 싶다면, 메모리 상에서 정수 6개를 담을 수 있는 공간을 확보하고, 원래 배열을 복사한 후, 마지막 공간에 새로운 정수를 추가하면 된다.

메모리에서 이미 정의된 배열 뒤에 새로운 수를 추가하고 싶으면 어떻게 될까? 바로 다음 주소에 새로운 수를 추가하고 싶은데, 그 공간이 비어있는지 알 수 없고 이런 위험성을 예방하기 위해 배열은 고정된 공간을 쓴다. 필요 이상으로 여유롭게 배열을 정의하면? 메모리 공간을 낭비하게 된다.

동적 배열(Dynamic Array)

동적배열은 정적배열과 달리 상황에 맞게 크기가 바뀐다. 동적배열은 내부적으로는 정적배열을 사용한다. 새로운 값을 추가하고 싶은데, 기존배열이 꽉 찼으면 크기를 2배 가량으로 적당하게 늘려준다. 정적배열의 크기를 상황에 맞게 조절하는 것이다.

파이썬의 리스트가 바로 동적배열이며, C 배열을 이용해 동적배열을 구현한 것이다. 이런 방식으로 동적배열에서는 삽일될 데이터를 미리 정의할 필요가 없다는 장점이 있다.

동적배열 추가연산(append operation) 시간복잡도

배열에 새로운 값을 추가하는 것을 추가연산, Append Operation이라고 한다. 정적배열에 남는 공간이 있을 때와 꽉 찼을 때로 나누어 보자.

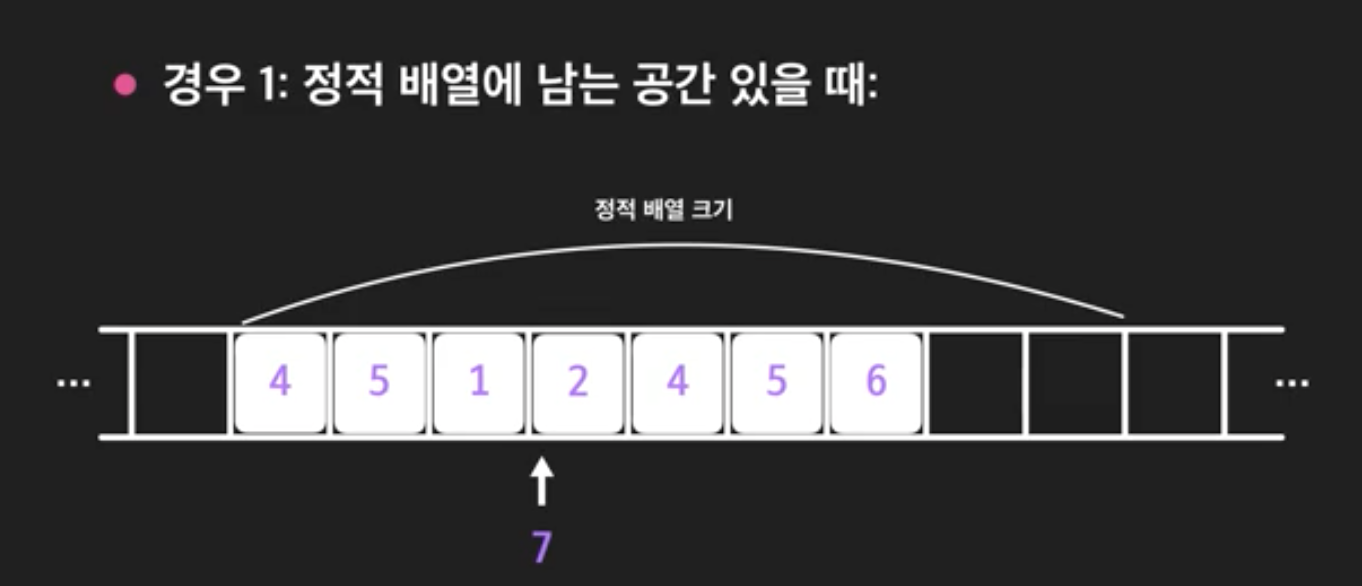
1. 정적 배열 남는 공간이 있을 때
비어있는 공간 중 가장 앞 쪽에 데이터를 저장하면 된다. 이떄 인덱스를 이요해 접근하기 때문에 O(1)의 시간복잡도를 가진다.

2. 정적 배열이 꽉 찼을 때
현재 배열보다 두 배로 큰 공간을 예약하고, 기본배열에서 새로운 배열로 값을 복사한다. 마지막으로 새 값을 추가한다. 기존에 저장된 데이터 개수를 n이라고 하고, 새 배열에 복사해야 할 땐 일일이 하나씩 해야 한다. 이 과정은 O(n)이 걸린다고 할 수 있다. 거기에 새 값을 추가하는 O(1) 시간이 걸려, 총 O(n+1) = O(n)이라고 할 수 있다.

분할 상환 분석

추가연산을 할 때
최고의 경우 : O(1)이고, 이 경우는 자주 일어난다.
최악의 경우 : O(n)이고, 이 경우는 가끔 일어난다.

그래서 동적배열에 값을 추가하는 데 O(n)이 걸린다고 하는 건 비합리적이다. 보통 시간복잡도는 가장 최악의 경우를 다루지만, 이처럼 비합리적인 상황이 종종 있다. 이런 경우 다르게 계산하는 몇 가지 방법들이 존재한다. 그 중, 분할상환분석을 알아보자

분할 상환 분석(Amortized Analysis)
같은 동작을 n번 했을 때 드는 시간이 X일떄, 동작을 한 번 하는 데에 걸리는 시간은 X/n 이라고 할 수 있다.

분할상환 = 할부 라고 봐도 된다.

시간 복잡도를 최악의 경우로 얘기하지 않고, 평균을 내서 얘기하는 것이다. 그럼 조금 더 합리적인 시간 복잡도를 구할 수 있겠죠?

동적배열 삽입연산(Insert Operation)

아무 위치에 데이터를 추가할 때는 삽입이라고 한다. 이것도 마찬가지로 정적배열에 남는 공간이 있을 때와 꽉 찼을 때로 나누어 볼 수 있다.

아래처럼 정적배열에 남는 공간이 있을 때, 7이라는 수를 넣고 싶으면 그 뒤에 있는 수들을 한 칸씩 뒤로 밀어 넣어야 한다. 이떄 시간복잡도는 최악의 경우에 인덱스 0번에 요소를 추가하는 경우니까, 현재 배열에 저장된 n개의 데이터를 모두 뒤로 한 칸씩 밀고, 새로운 수를 넣어야 하니, O(n+1) = O(n) 이 걸린다.

배열이 꽉 찬 경우, 기존 배열의 2배인 새로운 배열을 만들고 기존 데이터를 복사해온다. 그리고 이후 과정은 위와 동일하다. 새로운 배열에 요소를 복하는 데에 O(n), 뒤로 미는 경우 O(n), 인덱스에 원하는 데이터를 저장하는 건 O(1)으로, O(2n+1) = O(n) 이 걸린다.

따라서 삽입연산의 시간복잡도는 O(n) 이다.

배열과 동적배열 정리

연산에 따른 시간 복잡도

	배열	동적배열
접근	O(1)	O(1)
탐색	O(n)	O(n)
삭제	N/A	O(n), 맨뒤: O(1)
삭제	N/A	O(n), 맨뒤: O(1)

배열 : 크기가 고정되어 있기 때문에 낭비하는 공간 X
동적배열 : 공간을 낭비할 수도 있고, 안 할 수도 있다.