[자료구조] 링크드 리스트

링크드 리스트(Linked List)

• 데이터를 순서대로 저장
• 요소를 계속 추가할 수 있다

상황에 따라 링크드 리스트, 동적배열을 사용한다.

노드라는 단위의 데이터를 저장하고, 데이터가 저장된 각 노드들을 순서대로 연결시켜 만든 자료구조다.

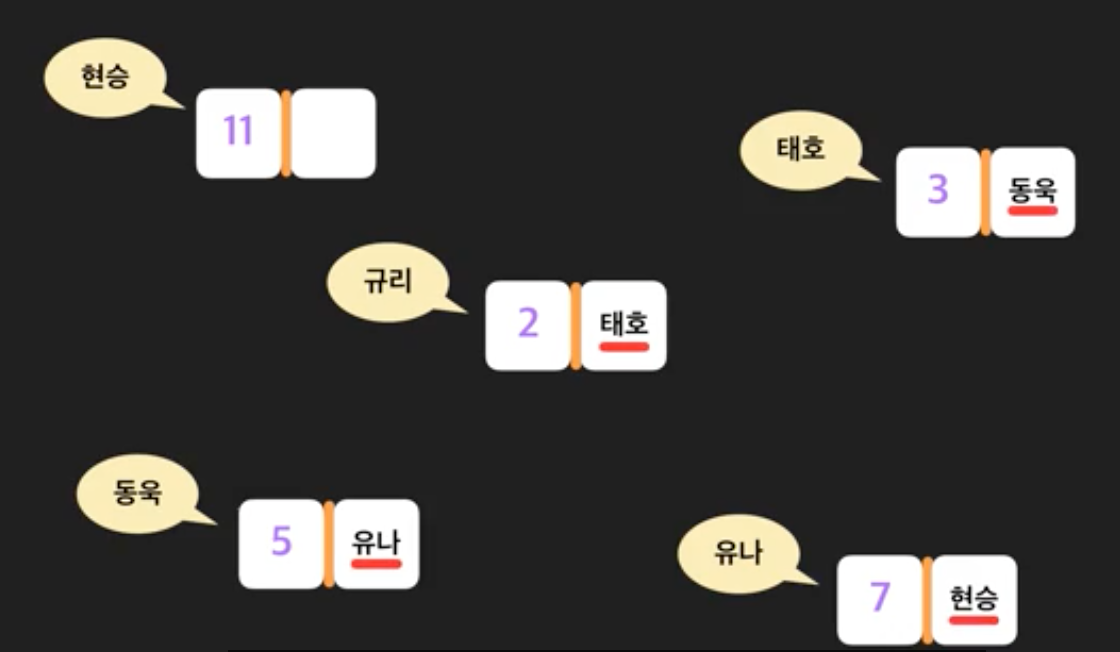
각 노드에 이름을 붙여주고, 그 노드에 숫자를 부여한다. 이때 흩어져 있는 노드를 순서대로 연결시키고 싶다면, 즉, 오름차순 정렬로 만들고 싶다면 특정 노드에 다음으로 올 노드의 이름을 붙여주면 된다.

이렇게 노드끼리 연결되어 있다고 해서 Linked List, 연결 리스트라고 한다.

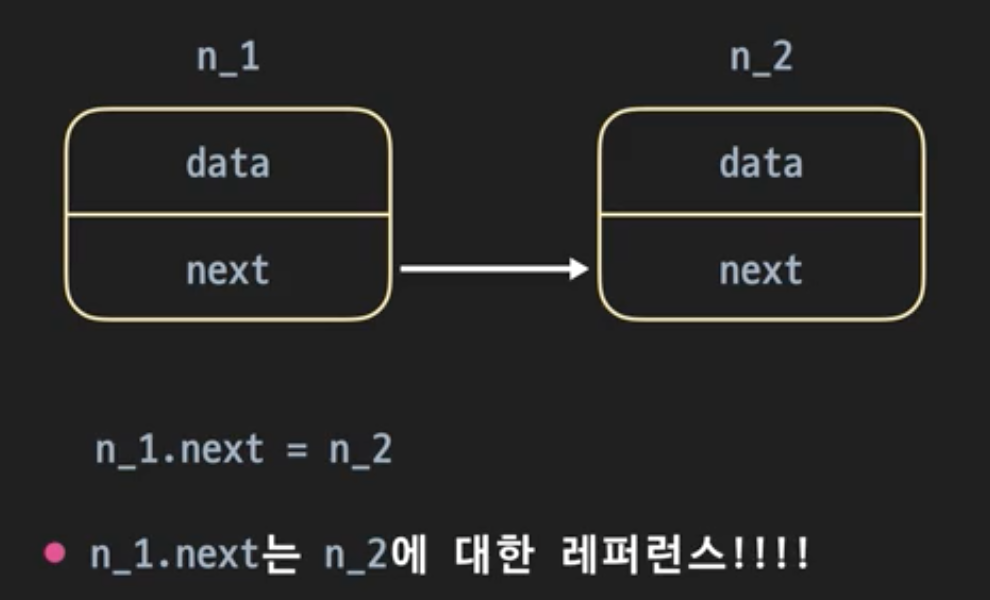
각 노드(Node) 는 하나의 객체로 표현된다. 그리고 각 노드 개체에는 data와 next 라는 두 가지 속성이 있다.

여기서 data에는 노드에 저장하고 싶은 값, next속성은 다음 노드에 대한 레퍼런스이다.

가장 첫 번째 노드 객체의 메모리 주소만 알고 있으면 next 속성을 타고 가서 연결되어 있는 모든 노드를 접근할 수 있다. 이떄 첫 번째 노드 객체를 head 라고 한다. 배열이나 동적배열처럼 정보를 원하는 순서로 저장할 수 있다. 그러나 실제 메모리에는 여기저기 흩어져 있다.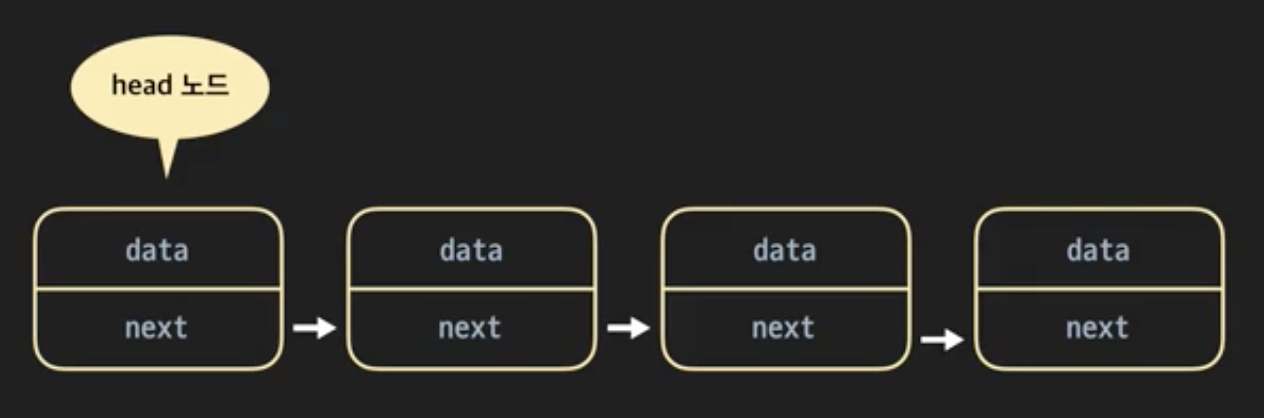

링크드 리스트 파이썬 구현

1. 노드 클래스와 간단한 링크드 리스트 만들기

class Node:
  """링크드 리스트의 노드 클래스"""
  def __init__(self, data):
   self.data = data # 노드가 저장하는 데이터
   self.next = None # 다음 노드에 대한 레퍼런스

# 데이터 2, 3, 5, 7, 11을 담는 노드를 생성
head_node = Node(2)
node_1 = Node(3)
node_2 = Node(5)
node_3 = Node(7)
tail_node = Node(11)

# 노드들을 연결
head_node.next = node_1
node_1.next = node_2
node_2.next = node_3
node_3.next = tail_node

# 노드 순서대로 출력
iterator = head_node
while iterator is not None: # 마지막 tail_node의 next 속성은 None이기 때문에 그 전까지만 반복문 돌아감
  print(iterator.data)
  iterator = iterator.next

2 3 5 7 11 순서대로 잘 출력된다.

2. 링크드 리스트 추가연산

이번에는 추가연산도 할 수 있도록 클래스를 만들어보자.

class LinkedList:
  """링크드 리스트 클래스"""
  def __init__(self):
    self.head = None
    self.tail = None

  def append(self, data):
    """링크드 리스트 추가 연산 메소드"""
    new_node = Node(data)
    if self.head is None: # 링크드 리스트가 비어있을 때
      self.head = new_node
      self.tail = new_node
    else:  # 링크드 리스트가 비어있지 않을 때
      self.tail.next = new_node
      self.tail = new_node

# 새로운 링크드 리스트 생성
my_list = LinkedList()

# 링크드 리스트에 데이터 추가
my_list.append(2)
my_list.append(3)
my_list.append(5)
my_list.append(7)
my_list.append(11)

# 링크드 리스트 출력
iterator = my_list.head
while iterator is not None:
  print(iterator.data)
  iterator = iterator.next

3. 링크드 리스트 str 메소드

링크드 리스트를 문자열로 표현하는 __str__ 메소드를 정의해보자.

def __str__(self):
	"""링크드 리스트를 문자열로 표현해서 리턴하는 메소드"""
    res_str = "|"

	# 링크드  리스트 안에 모든 노드를 돌기 위한 변수. 일단 가장 앞 노드로 정의한다.
    iterator = self.head

	# 링크드  리스트 끝까지 돈다
    while iterator is not None:
    	# 각 노드의 데이터를 리턴하는 문자열에 더해준다
        res_str += f" {iterator.data} |"
        iterator = iterator.next  # 다음 노드로 넘어간다

	return res_str

위 메서드를 클래스에 추가하고 확인해보자

# 새로운 링크드 리스트 생성
linked_list = LinkedList()

# 링크드 리스트에 데이터 추가
linked_list.append(2)
linked_list.append(3)
linked_list.append(5)
linked_list.append(7)
linked_list.append(11)

print(linked_list)  # 링크드 리스트 출력
# | 2 | 3 | 5 | 7 | 11 |

4. 링크드 리스트 접근 연산

특정 위치에 있는 노드를 리턴하는 연산인 접근연산을 구현해보자.
링크드 리스트는 레퍼런스를 통해 순서를 저장하기 때문에 한 번에 원하는 위치의 데이터에 접근할 수 없고, 인덱스 x에 있는 노드에 접근하려면 head에서 다음 노드로 x번 가야한다.

아래 함수를 클래스에 추가해주자.

def find_node_at(self, index):
	"""링크드 리스트 접근 연산 메소드. 파라미터 인덱스는 항상 있다고 가정"""
    iterator = self.head

	for _ in range(index):
    iterator = iterator.next

	return iterator

테스트 코드

# 새로운 링크드 리스트 생성
linked_list = LinkedList()

# 링크드 리스트에 데이터 추가
linked_list.append(2)
linked_list.append(3)
linked_list.append(5)
linked_list.append(7)
linked_list.append(11)

# 링크드 리스트 노드에 접근(데이터 가져오기)
print(linked_list.find_node_at(2).data)

# 2번 인덱스에 접근해서 5-> 13 으로 데이터 바꾸기
linked_list.find_node_at(2).data = 13

print(linked_list)

링크드 리스트 접근의 시간복잡도

배열은 인덱스와 상관없이 한 번에 접근할 수 있는 반면, 링크드 리스트 접근의 시간복잡도는 O(n)의 시간복잡도를 가진다.

5. 링크드 리스트 탐색연산

리스트에 특정 값이 있는지 탐색하는 탐색연산을 구현해보자. LinkedList 클래스에 아래 함수를 넣어준다. 메소드 find_node_with_data는 찾으려는 데이터를 파라미터 data로 받아서 링크드 리스트 내에서 원하는 데이터를 갖고 있는 노드를 리턴합니다.단, 원하는 데이터가 링크드 리스트 안에 없을 때는 None을 리턴합니다.

def find_node_with_data(self, data):
    """링크드 리스트에서 탐색 연산 메소드. 단, 해당 노드가 없으면 None을 리턴한다"""
    iterator = self.head
    
    while iterator is not None:
        if iterator.data == data:
            return iterator
        else:
            iterator = iterator.next

테스트 코드

# 새로운 링크드 리스트 생성
linked_list = LinkedList()

# 여러 데이터를 링크드 리스트 마지막에 추가
linked_list.append(2)
linked_list.append(3)
linked_list.append(5)
linked_list.append(7)
linked_list.append(11)

# 데이터 2를 갖는 노드 탐색
node_with_2 = linked_list.find_node_with_data(2)

if not node_with_2 is None:
    print(node_with_2.data)
else:
    print("2를 갖는 노드는 없습니다")

# 데이터 11을 갖는 노드 탐색
node_with_11 = linked_list.find_node_with_data(11)

if not node_with_11 is None:
    print(node_with_11.data)
else:
    print("11를 갖는 노드는 없습니다")

# 데이터 6 갖는 노드 탐색
node_with_6 = linked_list.find_node_with_data(6)

if not node_with_6 is None:
    print(node_with_6.data)
else:
    print("6을 갖는 노드는 없습니다")

6. 링크드 리스트 삽입 연산

클래스에 다음 메소드도 추가해준다.

def insert_after(self, previous_node, data):
    """링크드 리스트 주어진 노드 뒤 삽입연산 메소드"""
    new_node = Node(data)

    # 가장 마지막 순서 삽입
    if previous_node is self.tail:
        self.tail.next = new_node```
코드를 입력하세요

    self.tail = new_node

else: # 두 노드 사이에 삽입
    new_node.next = previous_node.next
    previous_node.next = new_node

테스트 코드
```py
# 새로운 링크드 리스트 생성
linked_list = LinkedList()

# 여러 데이터를 링크드 리스트 마지막에 추가
linked_list.append(2)
linked_list.append(3)
linked_list.append(5)
linked_list.append(7)
linked_list.append(11)

# 삽입연산 사용코드
node_2 = linked_list.find_node_at(2) # 인덱스 2에 있는 노드 접근
linked_list.insert_after(node_2, 6) # 인덱스 2 뒤에 6 삽입

print(linked_list)

7. prepend 연산

맨 앞에 새로운 노드를 추가할 수 있는 연산을 수행하는 prepend 함수를 만들어보자.

def prepend(self, data):
    """링크드 리스트의 가장 앞에 데이터 삽입"""
    new_node = Node(data)
    if self.head is None:
      self.head = new_node
      self.tail = new_node
    else:
      new_node.next = self.head # 새로운 노드의 next을 기존 노드의 head로 설정
      self.head = new_node      # 리스트의 head_node를 새 노드로 설정

8. delete 연산

링크드리스트의 노드를 삭제하는 연산을 만들어보자. 주어진 노드 뒤 노드를 삭제한다. 이것도 마찬가지로 두 가지 경우로 나뉘는데, 삭제하고자 하는 노드가 tail인지 아닌지로 나눈다.
지우려는 노드가 tail 노드일때, 전 노드가 가리키는 걸 None으로 바꾼다.

지우려는 노드가 tail 노드가 아닐때, 지우고자 하는 노드의 next를 지우고자 하는 노드 다음 노드로 설정한다.

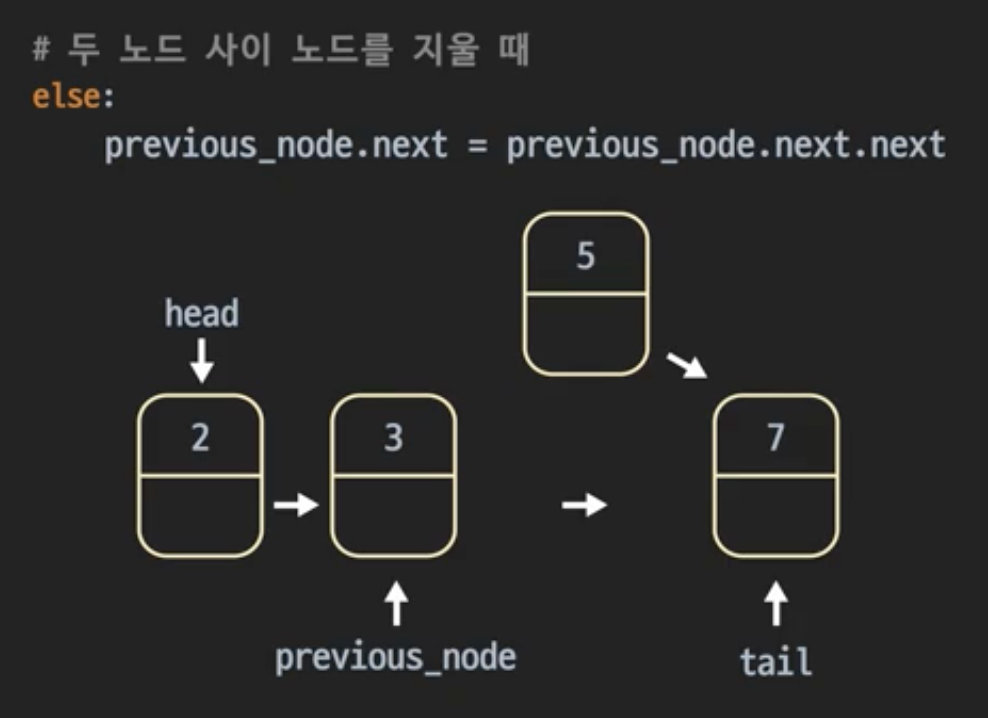
def delete_after(self, previous_node):
    """링크드 리스트 삭제연산. 주어진 노드 뒤 노드를 삭제한다."""
    data = previous_node.next.data
    if previous_node.next is self.tail: # 지우려는 노드가 tail노드일 때,
        previous_node.next = None # 전 노드가 가리키는 걸 None으로 만든다.
        self.tail = previous_node
    else: # 지우려는 노드가 tail노드가 아닐때
        previous_node.next = previous_node.next.next

    return data  # 지우려는 노드를 반환

테스트코드

# 새로운 링크드 리스트 생성
linked_list = LinkedList()

# 여러 데이터를 링크드 리스트 앞에 추가
linked_list.prepend(11)
linked_list.prepend(7)
linked_list.prepend(5)
linked_list.prepend(3)
linked_list.prepend(2)

print(linked_list)  # 링크드 리스트 출력


# 링크드 리스트 삭제연산 
node_2 = linked_list.find_node_at(2) # 인덱스 2번의 노드에 접근
linked_list.delete_after(node_2) # 인덱스 2번 뒤의 데이터를 삭제
print(linked_list) # 링크드리스트 출력

9. 맨 앞 노드 삭제 pop_left

바로 전 레슨에서 배운 삭제는 삽입과 마찬가지의 문제가 있는데요. 주어진 노드의 다음 노드를 삭제하기 때문에 head 노드를 삭제할 수 없습니다. 전과 마찬가지로 head 노드도 지울 수 있도록 메소드를 추가하겠습니다.
메소드 pop_left는 파라미터로 self 이외에 아무것도 받지 않으며, 링크드 리스트의 head 노드를 삭제해줍니다. pop_left 메소드는 링크드 리스트에서 삭제하는 노드의 데이터를 리턴합니다.

def pop_left(self):
    """링크드리스트의 가장 앞 노드 삭제 메소드. 단 링크드 리스트에 항상 노드가 있다고 가정"""
    data = self.head.data # 삭제할 노드
    if self.head is self.tail:
        self.head = None
        self.tail = None
    else:
        # 링크드리스트의 head를 맨 앞 노드의 바로 다음 노드로 설정
        self.head = self.head.next
    return data # 삭제된 노드의 데이터를 리턴

테스트코드

# 새로운 링크드 리스트 생성
linked_list = LinkedList()

# 여러 데이터를 링크드 리스트 앞에 추가
linked_list.prepend(11)
linked_list.prepend(9)
linked_list.prepend(5)
linked_list.prepend(3)
linked_list.prepend(2)

print(linked_list) # 링크드 리스트 출력

# 가장 앞 노드 계속 삭제
print(linked_list.pop_left())
print(linked_list.pop_left())
print(linked_list.pop_left())
print(linked_list.pop_left())
print(linked_list.pop_left())

print(linked_list) # 링크드 리스트 출력
print(linked_list.head)
print(linked_list.tail)

링크드리스트 연산의 시간 복잡도

접근

인덱스 x에 있는 데이터에 접근하려면 링크드 리스트의 head 노드부터 x 번 다음 노드를 찾아서 가야 한다. 2번째 노드에 접근하려면 1번 이동해야 한다. 즉 1번 인덱스로 가려면 1번 이동, 100번 인덱스로 가려면 100번 이동.. 해야 하므로 최악의 경우 마지막 순서에 있는 노드에 접근하는 경우 n-1번 이동해야 한다. 즉, O(n)의 시간 복잡도를 갖는다.

탐색

링크드리스트 탐색 연산은 배열을 탐색할 떄와 같은 방법으로 한다. 가장 앞 노드부터 다음 노드를 하나씩 보면서 원하는 데이터 값을 찾는다. 이런 탐색방법을 선형탐색이라 한다. 접근과 마찬가지로 링크드 리스트 안에 찾는 데이터가 없을 때, 또는 데이터가 마지막 노드에 있는 최악의 경우 n개의 노드를 모두 다 봐야 한다. 따라서 O(n)의 시간 복잡도를 갖는다.

삽입/삭제

삽입과 삭제의 경우 next 레퍼런스를 수정하여 연결을 끊거나 연결하는 것으로, 주변 노드에 연결된 레퍼런스만 수정한다. 따라서 이 연산은 어떤 노드를 삽입or삭제하든 상관없이 걸리는 시간이 변함없다. 따라서 O(1)의 시간 복잡도를 갖는다.

시간복잡도

연산	시간복잡도
접근	O(n)
탐색	O(n)
삽입	O(1)
삭제	O(1)

현실적인 삽입/삭제 시간 복잡도

하지만 조금 더 현실적으로 생각해보자면, 삽입과 삭제연산들은 특정 노드를 넘겨줘서 이 노드 다음 순서에 데이터를 삽입하거나 삭제한다. 그럼 이 연산들에 넘겨주는 노드, 파라미터 previous_node를 먼저 찾아야 한다. 즉, 탐색이나 접근 연산을 통해 가지고 와햐 한다.

따라서 현실적으로는 O(n+1)의 시간 복잡도를 가진다고 할 수 있다.

연산	현실적인 시간복잡도
접근	O(n)
탐색	O(n)
삽입	O(n+1)
삭제	O(n+1)

반면 맨 앞이나, 맨 뒤 노드를 삭제 및 추가하는 연산인 pop_left, prepend, append는 head와 tail 노드를 한 번에 찾을 수 있으니 접근하는 데 O(1), 연산을 수행하는 데 O(1)이 걸린다.
tail 노드를 삭제하는 경우에는 바로 전 노드가 필요하다. 바로 전 노드를 찾으려면 head 노드에서 n-2번 다음 노드로 이동해야 한다. 따라서 접근하는 데에 O(n-2)가 걸린다. 따라서 tail노드 전 노드에 접근해서 tail 노드를 삭제하는 연산은 O(n+1) 이 걸린다.
| 연산 | 시간복잡도 |
| --- | --- |
| 가장 앞에 접근 + 삽입 | O(1+1) |
| 가장 앞에 접근 + 삭제 | O(1+1) |
| 가장 뒤에 접근 + 삽입 | O(1+1) |
| tail노드 전 노드에 접근 + 삭제 | O(n+1) |