6장 다양한 가설검정
6.1 다양한 가설검정
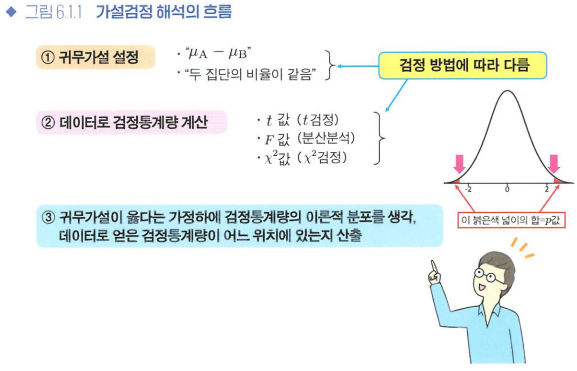
- 가설검정 방법 선택
가절검정 방법을 선택할 때는 데이터 유형, 표본의 수, 양적 변수 분포의 성질을 먼저 확인하자.
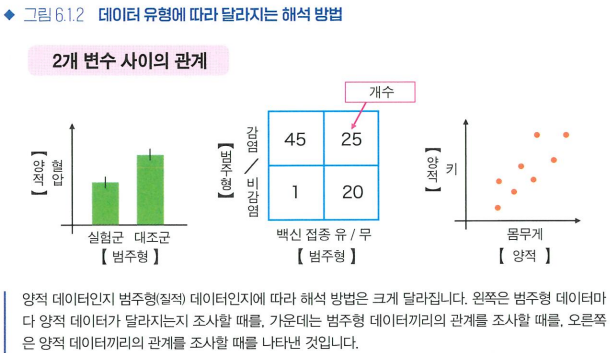
- 데이터 유형
- 2개의 양적 변수 관계: 산점도
- 2개의 질적 변수(범주형) 관계: 분할표
- 표본의 수(집단의 수)
- 1표본: 1변수 데이터 조사(1개의 모집단 분포에 대한 가설 검증)
- 2표본 이상: 집단 간 차이 조사
- 3표본 이상: 다중비교라 불리는 보정 방법 필요
- 양적 변수의 성질
데이터에 양적 변수가 있는 경우, 어떤 분포를 취하는지가 검정 방법을 선택할 때 중요하다.
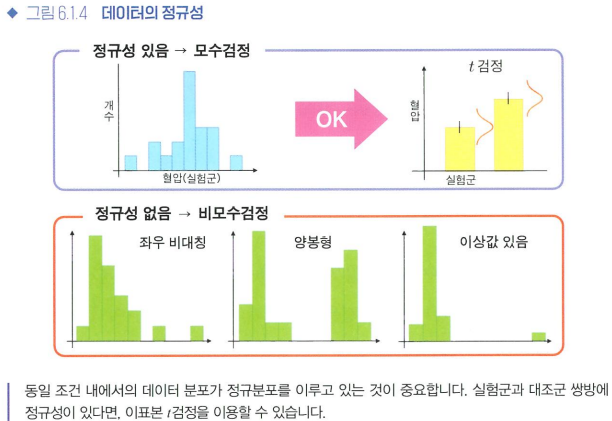
- 모수검정: 모집단이 특정 분포를 따른다는 가정을 둔 가설검정, 대부분은 정규분포인 경우
ex) t검정: 모집단이 정규분포라고 가정
- 정규성: 데이터가 정규분포로부터 얻어졌다고 간주할 수 있는 성질
- 비모수검정: 모집단분포가 특정 분포라고 가정할 수 없는 경우, 평균이나 표준편차 등의 모수(파라미터)에 기반을 두지 않는 방법
- 등분산성: 집단 간 평균값을 비교하는 경우에, 집단끼리 분산이 동일하다고 가정하는 방법
- 데이터 유형
6.2 대푯값 비교
-
모수검정의 평균값 비교
-
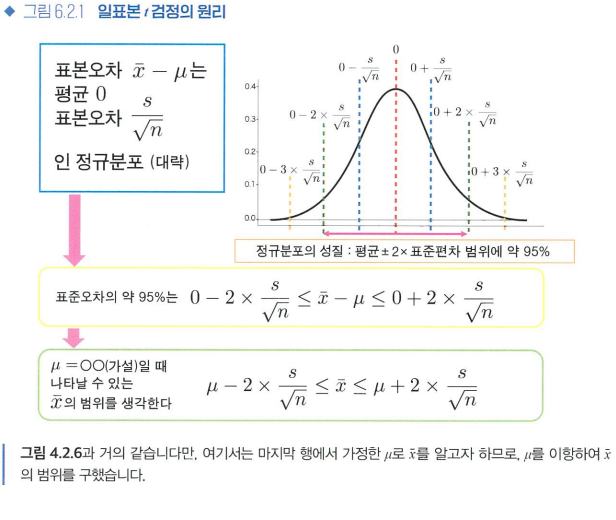
일표본 t검정: 어떤 평균값의 모집단에서 표본을 얻었는가를 조사

- 유의수준 α=0.05에서 p>=0.05라면 대립가설 " "이라고 말할 수 없다.
- 유의수준 α=0.05에서 p<0.05라면 대립가설 " "이라고 판단할 수 있다.
- mu는 연구에서 의미 있는 값으로 선정 -> 가설검정이 아니라, 95% 신뢰구간을 구하는 방법
-
이표본 t검정

- 데이터에 정규성이 있어야 한다. -> 등분산성 가정
- 분산이 일치하지 않는 경우, 웰치의 t검정(단, 정규성은 있어야 한다.)
-
대응 관계가 없는 검정, 대응 관계가 있는 검정
피험자들의 차이 = 0
피험자들의 차이 != 0
-
정규성 조사
- Q-Q 플롯: 시각적으로 판단할 수 있는 분위수-분위수 그림
- 샤피로-윌크 검정: 가설검정으로 조사
- 콜모고로프-스미르노프(K-S) 검정: 이론적인 분포와 비교
-
등분산성 조사
t검정과 분산분석에는 데이터가 분산이 같은 모집단으로부터 획득되었다는 조건이 필요하다.
분산이 같다는 가설을 조사하는 검정: 바틀렛 검정, 레빈 검정
- 귀무가설 "2개 모집단의 분산은 같다." <- p>=0.05
- 대립가설 "2개 모집단의 분산은 같지 않다." <- p<0.05
-
-
비모수검정의 대푯값 비교
- 비모수 버전의 2개 표본 대푯값 비교
정규성이 없는 경우, 평균값 대신 분포의 위치를 나타내는 대푯값에 주목- 윌콕슨 순위합 검정: 각 데이터 값의 순위에 기반한 검정
- 귀무가설 "2개 모집단의 위치가 같다."
- 대립가설 "2개 모집단의 위치가 다르다."
- 맨-휘트니 U검정: 비교할 2개 집단의 분포 모양 자체가 같아야 사용할 수 있음
- 플리그너-폴리셀 검정, 브루너-문첼 검정: 분포 형태가 같지 않을 때도 사용할 수 있음
- 윌콕슨 순위합 검정: 각 데이터 값의 순위에 기반한 검정
- 비모수 버전의 2개 표본 대푯값 비교
-
분산분석(3개 집단 이상의 평균값 비교)
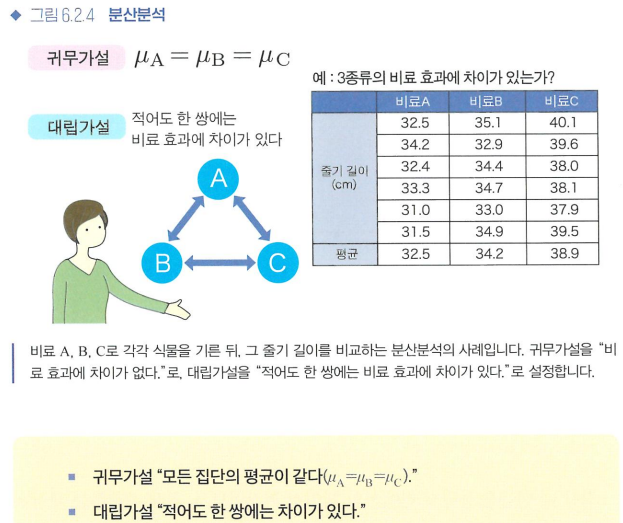
- 분산분석의 원리
데이터 전체 평균 = x^
각 집단의 평균 = x^A, x^B, x^C
각 데이터 x_i
-> x_i - x^ = (x_i - x^c) + (x^c - x^)
-> 각 데이터의 전체 평균과의 차이(분산) = 집단 내의 분산(집단 내 변동) + 집단 간의 분산(집단 간 변동)
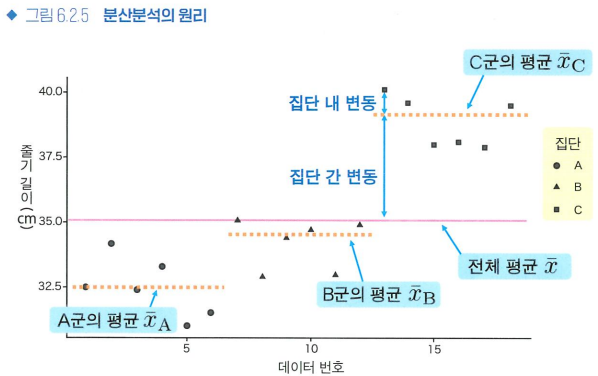
- 집단 내 변동: 동일 조건에서의 데이터 퍼짐이므로, 원래 존재하는 무작위 오차의 크기
- 집단 간 변동: 집단 간 차이가 있다면 큰 데이터 퍼짐, 없다면 집단 내 편차와 같은 정도의 작은 데이터 퍼짐
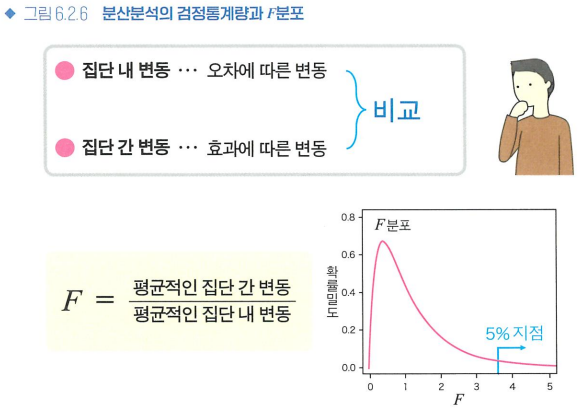
- F값 = (평균적인 집단 간 변동)/(평균적인 집단 내 변동)
- F분포: F값이 p(F값 이상으로 극단적인 값이 나올 확률)보다 오른쪽에 있다면 유의수준 α=0.05에서 통계적으로 유의미한 집단 간 차이가 있다.
- 분산분석의 원리
-
다중비교 검정
- 집단의 수가 늘어날 수록 제1종 오류가 일어나기 쉬워진다.
-> 다중성 문제를 회피하고자 다중비교 검정 - 다중비교 검정: 검정을 반복하는 만큼, 유의수준을 엄격한 값으로 변경
- 여러 다중비교 방법
- 본페로니 교정: 매 검정에서 α/k(유의수준/검정 반복 횟수)를 기준으로 가설검정을 하는 방법, p<α/k라면 대립가설 채택
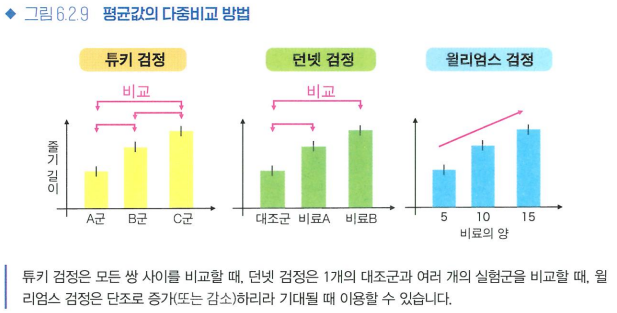
-> 간편하지만 검정력이 낮다 - 튜키 검정: 분산분석을 시행한 다음에는 검정력을 개선한 튜키 검정을 사용하기도 한다
- 던넷 검정: 대조군과의 비교에만 관심 있을 때
- 윌리엄스 검정: 집단 간에 순위를 매길 수 있는 경우
- 본페로니 교정: 매 검정에서 α/k(유의수준/검정 반복 횟수)를 기준으로 가설검정을 하는 방법, p<α/k라면 대립가설 채택
- 언제나 분산분석이 필요할까?
일반적인 다중비교 검정: 최초에 분산분석 실행 후 p<α 일때 사용
분산분석에서 유의미하지 않았지만 다중비교에서는 유의미한 쌍이 있기도 한다. -> 분산분석을 실행하지 않고, 다중비교만 실행해도 된다.
- 3집단 이상의 비모수검정
- 크러스컬-윌리스 검정: 정규성이 없는 집단이 1개 이상
- 스틸-드와스 검정: 튜키 검정에 상응
- 스틸 검정: 던넷 검정
- 집단의 수가 늘어날 수록 제1종 오류가 일어나기 쉬워진다.
6.3 비율 비교
-
범주형 데이터
- 양적 변수: 모집단의 평균값을 추정하거나 모집단을 대상으로 가설을 세워 가설검정 시행
- 범주형 변수: (모집단의 파라미터인 앞면이 나올 확률)P를 추정하거나 P에 관련된 가설을 세워 검정
-
이항검정
하나의 범주가 확률 P, 또 하나의 범주가 확률 1-P로 나타나는지를 조사

p값은 이항분포를 따른다.
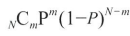
p = 0.043 -> 유의수준 α=0.05에서 통계적으로 유의미하다.
-
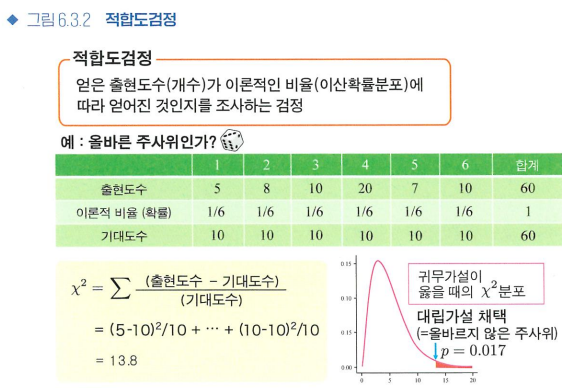
카이제곱검정: 적합도검정
범주가 2개 이상일 때, 더 일반적인 이산확률분포에 이항검정의 방식을 적용하고 싶은 때 쓰는 검정

- 귀무가설의 확률분포에서 얻을 수 있는 기대도수 계산
기대도수 = 전체 개수 * 각 확률 -> 즉, 가장 나타나기 쉬운 실현값 - 카이제곱값: x^2 = sum(각 눈의 (실제 출현도수 - 기대도수)^2 / (기대도수))
-> 귀무 가설이 옳다면 카이제곱분포를 따른다 - 실제로 얻은 x^2값의 위치를 구하여 p값 도출
- 귀무가설의 확률분포에서 얻을 수 있는 기대도수 계산
-
카이제곱검정: 독립성검정
- 이항검정이나 카이제곱검정의 적합도검정: '데이터 VS 모집단' 확률분포 비교
- 카이제곱검정의 독립성 검정: 범주형 변수에서도 변수의 관계
-> 한쪽 변수의 범주가 바뀌었을 때 다른 쪽 변수의 범주 비율이 달라지지 않을 때 독립적이다.

- 기대도수 계산 -> x^2 계산 -> 분포 안의 위치에 따라 p값 구하고 대립가설이 채택되는지 확인

7장 상관과 회귀
7.1 양적 변수 사이의 관계를 밝히다
- 2개의 양적 변수로 이루어진 데이터
- 산점도: 변수 2개를 (x축 값, y축 값)으로 하여 각 값을 2차원 평면 위의 점으로 나타낼 수 있다.
- 상관: 2개 변수 사이의 관계성, 산점도를 이용하여 두 양적 변수의 관계를 시각화하면 어떤 관계인지 대략적으로 파악할 수 있다
주의점: 인과관계(원인, 결과)와 다르다, x축과 y축을 맞바꾸어도 상관없다
- 회귀: y= f(x) 함수를 통해 변수 사이의 관계를 공식화하는 것
- x: 설명변수, 독립변수
- y: 반응변수, 종속변수
- 'x에서 y'라는 방향성이 있다
- 회귀분석: 얻은 데이터에 잘 들어맞는 f(x)를 추정하고, 2개 변수 간 관계를 구한다
7.2 상관관계
-
피어슨 상관계수
- 2개의 양적 변수 간 관계의 강도를 정량화 하는 방법 중 하나
- 피어슨 상관계수(r) = 2개의 양적 변수 사이의 선형관계가 얼마나 직선 관계에 가까운가
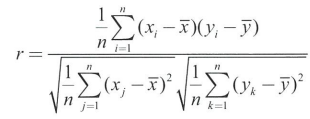
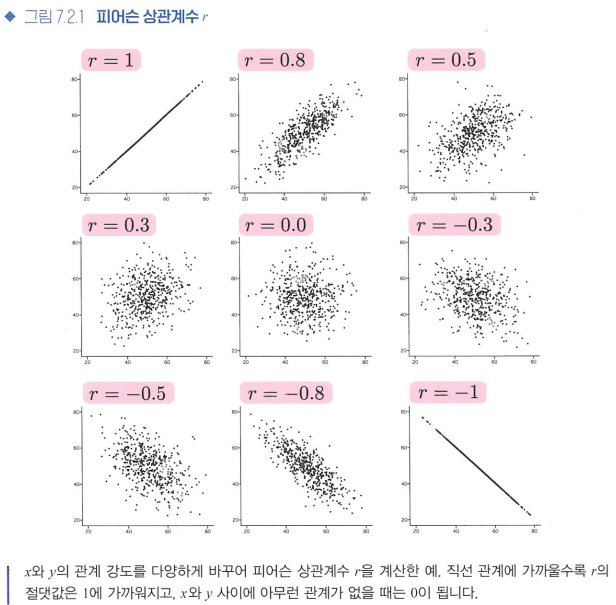

- 상관계수 r은 선형관계를 나타낸다
- 비선형관계는 r로 정량화할 수 없다
- 직선의 기울기 크기는 r과 관계가 없다
- 상관계수가 같은 다양한 데이터
같은 r을 가지고 있더라도, 비선형을 포함한 다양한 패턴이 있을 수 있다
- 정규성 검사
- 피어슨 상관계수 r은 x분포, y분포가 모두 정규분포라고 가정
- 한쪽에 조금이라도 정규성이 없다면 비모수 상관계쑤를 이용하자
-
비모수 상관계수
- x축, y축 중 적어도 하나 이상에 정규성이 없을 때, 스피어만 순위상관계수 p 사용을 권장
- 순위로 변환한 값의 선형관계
- p: -1~1 실수
- 주의점: 2개 변수가 처음부터 종속관계일 때
-
상관계수와 가설
- 상관계수의 가설검정
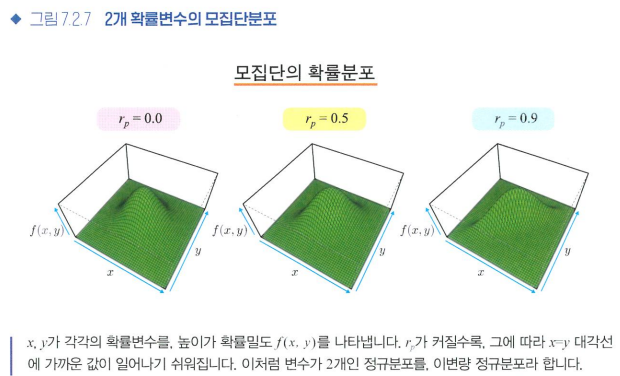
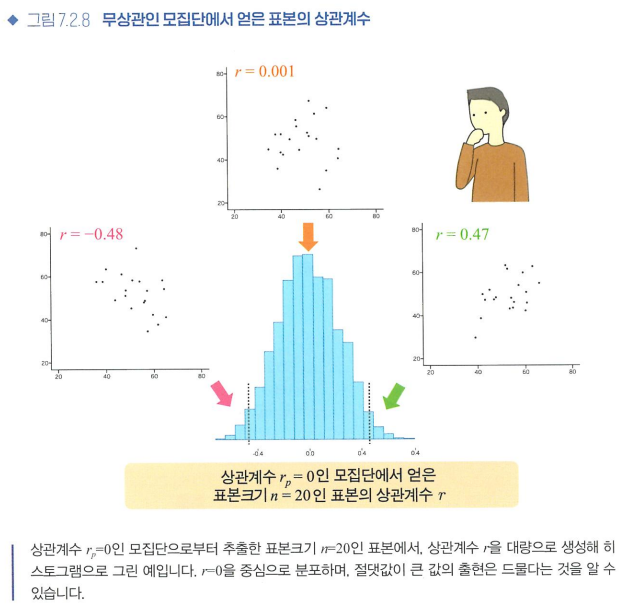
가설검정 시행 결과가 p<0.05임을 알고 나면 양의 상관이 있다고 주장 가능하다
- 표본크기와 가설검정
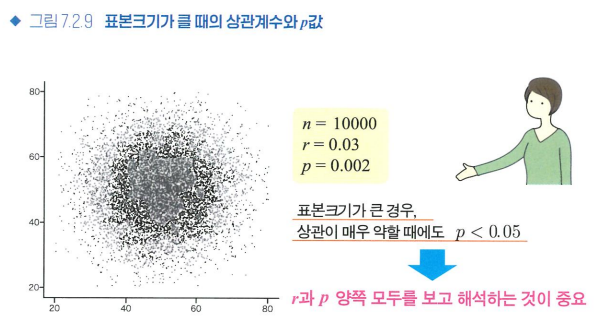
- 상관계수의 가설검정
-
비선형상관
'X가 Y에 관해, 또는 Y가 X에 관해 어느 정도의 정보를 포함하는지'의 관점에서 관계성 강도를 정량화하는 것
7.3 선형회귀
-
회귀분석이란?
- 회귀식: y=f(x)
- 회귀계수: 회귀식의 형태를 결정하는 파라미터 a, b
- 특정 평가기준에 따라 회귀의 '좋음(적합도)'을 평가하고, 이 회귀계수의 값을 구체적으로 구하는 것
- 화귀모형: y=a+bx+ε(확률오차)
회귀분석을 실행할 때 중요한 점은?
-- 어떤 회귀식을 적용할 것인가?
-- 어떻게 회귀식을 데이터에 적용할 것인가?
-- 얻은 회귀모형을 어떻게 평가할 것인가? - 최소제곱법
- 좋은 회귀 모형? -> 데이터와 회귀식의 차이가 가능한 한 작은 a와 b를 결정해보자
- 최소제곱법: 데이터와 모형 차이의 제곱을 모두 더한 값 E을 최소화하는 방법
-
회귀계수
E(a^) = a
E(b^) = b최량선형비편향추정량: 최소제곱법으로 얻은 추정량은 비편향추정량 중에서도 가장 정밀도가 높은(분산이 작은) 비편향추정량이 된다
- 회귀계수의 가설검정
b?
귀무가설 'b(기울기) = 0', 대립가설 'b != 0' -> 가설검정 실행
-> 가설검정 결과 p < 0.05
-> b != 0 주장 가능
-> x에 대해 b는 선형관계이다
- 95% 신뢰구간
모집단의 회귀계수를 추정 - 95% 예측구간
추정한 회귀모형을 기반으로 데이터 그 자체가 분포하는 구간
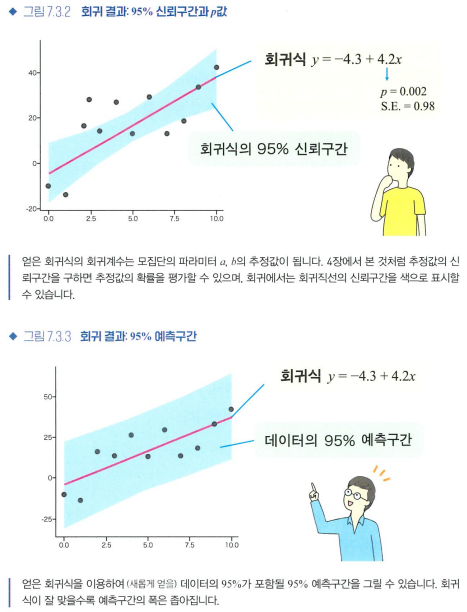
- 회귀계수의 가설검정
-
결정계수
회귀식이 잘 들어맞는지 평가하는 지표, R^2
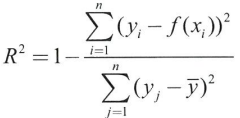
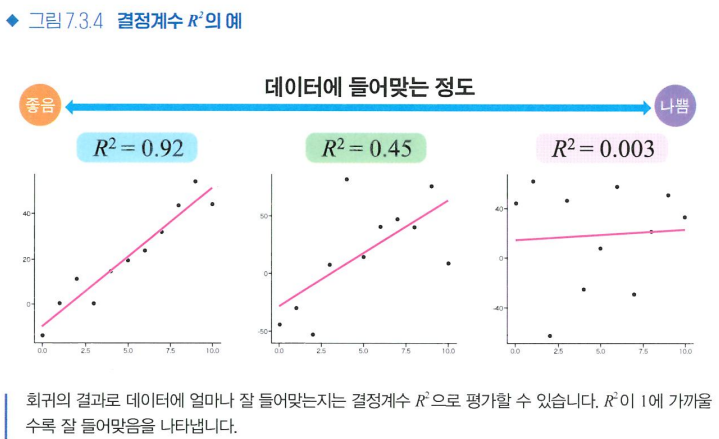
- 조정 결정계수: 설명변수 개수 k에 따라 조정한 결정계수
- k가 작을수록 R^2과 거의 비슷한 값이 된다
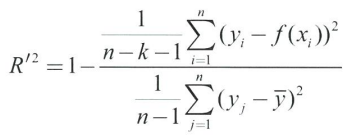
- k가 작을수록 R^2과 거의 비슷한 값이 된다
- 조정 결정계수: 설명변수 개수 k에 따라 조정한 결정계수