8장 통계 모형화
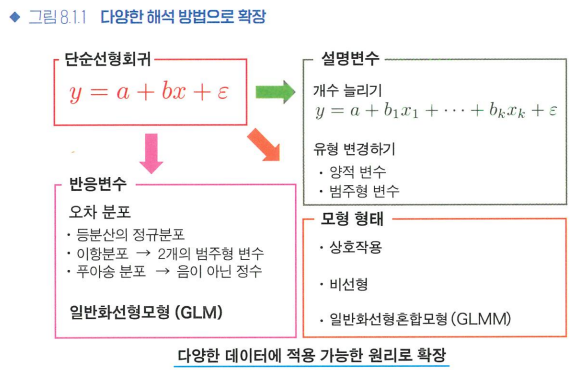
8.1 선형회귀 원리의 확장
-
선형회귀의 확장
- 설명변수의 개수 확장 or 유형 변경
- 반응변수의 유형 변경
- 회귀모형의 형태 변경
-
다중회귀
설명변수가 여러 개인 회귀
- 다중선형회귀모형
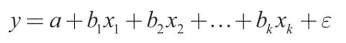
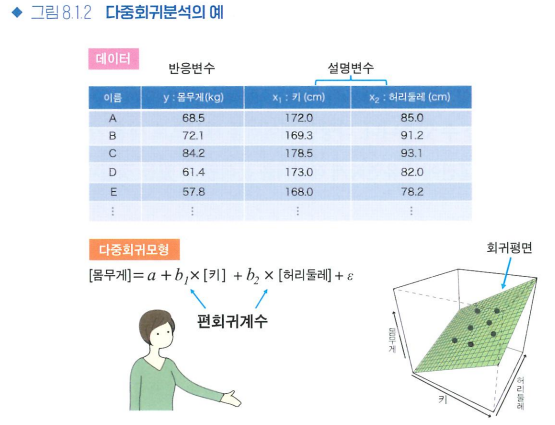
- 편회귀계수: 다중회귀에서의 기울기 b1, b2
- 회귀평면: 설명변수가 2개일 때 2차원의 회귀모형
- 다중회귀 결과를 읽는 방법
- 편회귀계수와 유의성에 주목!

- 편회귀계수는 모두 유의미
- p<0.05 -> 회귀모형의 설명력에 유의성이 있다
- 편회귀계수와 유의성에 주목!
- 다중선형회귀모형
-
편회귀계수
- 표준화편회귀계수
회귀분석을 시행하기 전에 각각의 설명변수를 평균 0, 표준편차 1로 변환 후, 회귀분석을 시행하여 구한 회귀계수
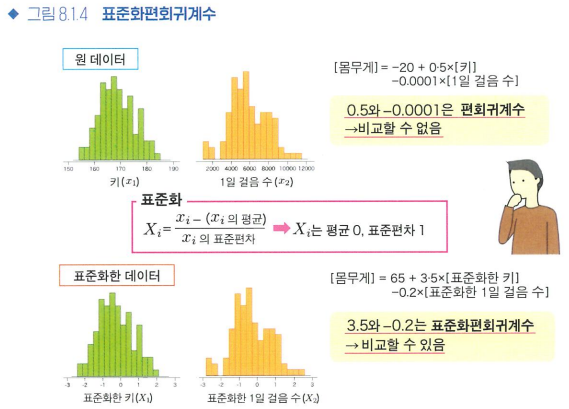
- 편회귀계수의 해석
상관계수가 1에 가까운 강한 상관이 있을 때는, 다중공선성이 있는지를 의심하고 대처
- 표준화편회귀계수
-
범주형 변수를 설명변수로
각 범주에 대해 가변수로 0 또는 1을 할당하고 회귀모형에 적용- 범주가 3개 이상일 때
ex) 혈액형 4개
1. 0/1 가변수를 (범주 개수 - 1)개 준비 -> 다중 공선성을 피하기 위함
2. (0,0,0), (1,0,0), (0,1,0), (0,0,1)
- 범주가 3개 이상일 때
-
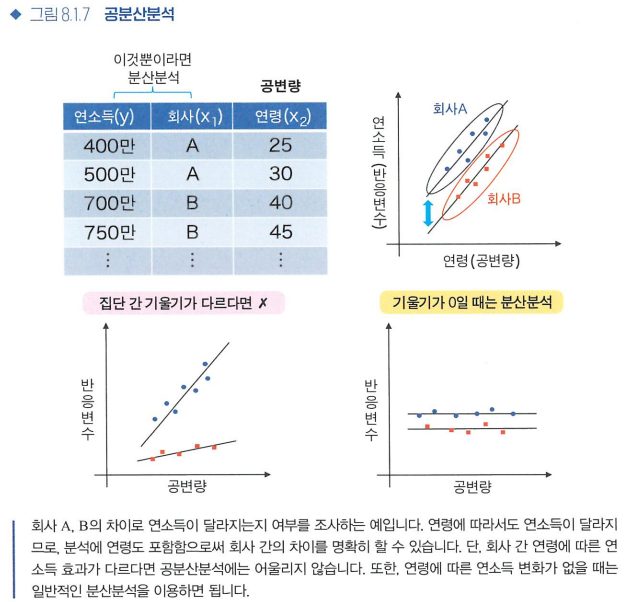
공분산분석
- 회귀분석의 관점에서 설명변수: 범주형 변수, 반응변수: 양적 변수
- 공분산분석: 일반적인 분산분석에 사용하는 데이터와 함께 양적 변수 데이터가 있는 경우에 후보가 되는 방법
- 공변량: 이때 새로 추가한 양적 변수
- 공분산분석의 조건
- 집단 간 회귀의 기울기가 서로 다르지 않아야 한다.
- 회귀계수가 0이 아니어야 한다.
-
고차원 데이터 문제
- 차원의 저주: 차원이 늘어날수록 파라미터 추정에 필요한 데이터 양이 폭발적으로 증가
- 차원이 증가할수록 다중공선성 문제가 일어나기 쉬우므로, 모형의 추정 정밀도가 떨어진다
- 이를 해결하기 위해 차원축소 방법을 이용하기도 한다.
- 차원의 저주: 차원이 늘어날수록 파라미터 추정에 필요한 데이터 양이 폭발적으로 증가
-
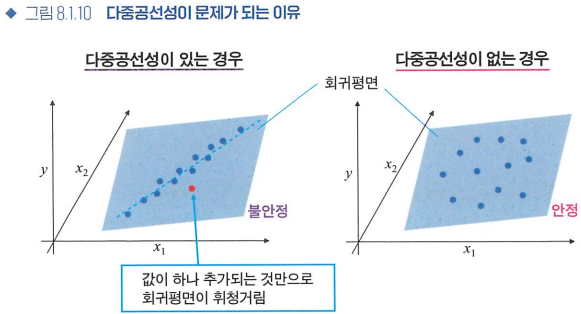
다중공선성
- 설명변수가 여러 개인 다중회귀에서 설명변수 사이에 강한 상관이 있는 경우, 다중공선성이 있다고 말한다.
- 다중공선성이 있다면 회귀계수의 추정오차가 커지는 문제가 발생할 가능성이 있다.
- 분산팽창인수 VIF
다중공선성 정도 측정
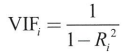
- VIF > 10: 2개 사이의 상관이 아주 강하다
- 다중공선성이 강하다고 판단 -> 서로 상관이 있는 2개 변수 중 하나를 없애거나, 차원 축소 방법을 이용하여 설명변수의 개수를 줄인다
- 다중공선성의 문제는 추정한 회귀계수를 해석하기 어렵다는 것
- 예측이 목적인 회귀라면, 우선순위는 예측이 좋은 모형을 얻는 것이므로, 다중공선성이 문제되지 않을 때도 흔하다
- 분산팽창인수 VIF
8.2 회귀모형의 형태 바꾸기
-
상호작용
설명변수 간의 상승효과, 선형회귀모형 안에서 곱셈 cx_ix_j로 나타낼 수 있다
- 설명변수가 양적 변수인 다중회귀모형에 상호작용항을 언제 넣는 것이 좋을까

- 설명변수가 양적 변수인 다중회귀모형에 상호작용항을 언제 넣는 것이 좋을까
-
이원배치 분산분석
다중배치 분산분석: 여러 개의 요인을 동시에 고려할 수 있는 분산분석
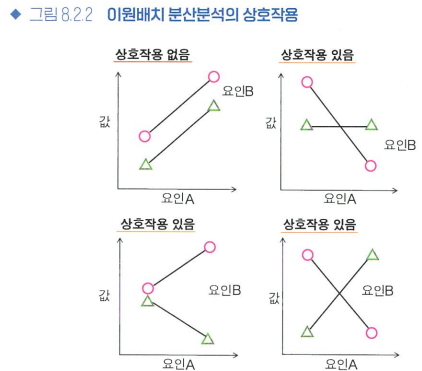
- 가설검정 결과 상호작용항이 유의미하지 않다면 상호작용이 없다고 보고, 각각의 주효과를 그대로 평가한다
- 가설검정 결과 상호작용항이 유의미하지 않다면 상호작용이 없다고 보고, 각각의 주효과를 그대로 평가한다
-
비선형회귀
- 선형모형
- 선형모형: 파라미터에 관해 선형 (2차식은 비선형이지만 파라미터에 관해서는 1차식인 선형이므로 선형모형이라고 한다)
- 비선형 모형을 적용할 때는 목적에 맞게 '적절한가'를 판단하자
- 결과 해석을 중시하는 일반적인 통계학 기준이라면, 1차 함수의 회귀모형을 이용하는 것이 보통적이다
- 예측을 중시하는 회귀모형이라면, 모형의 복잡도를 적당히 올려 예측 성능을 향상시키기도 한다.
- 비선형모형
그 모형을 사용하는지 합리적인 이유가 있어야만 한다
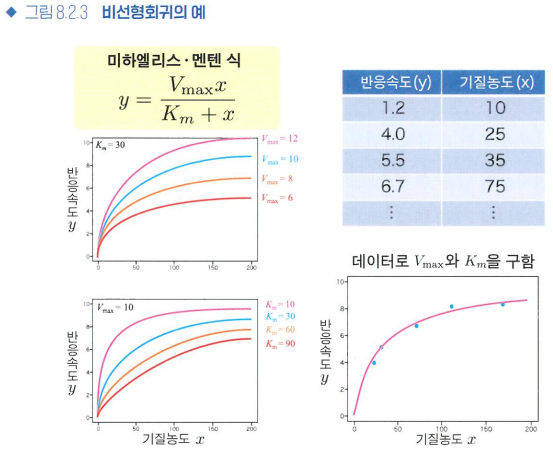
- 선형모형
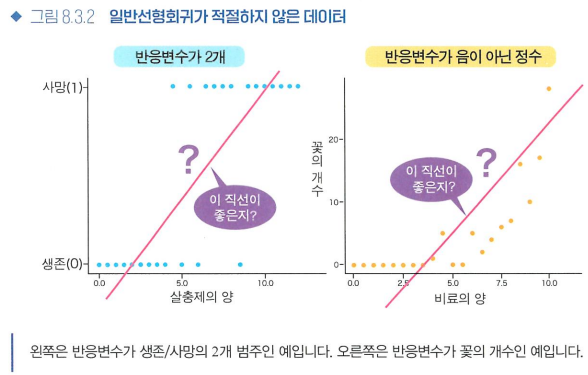
8.3 일반화선형모형의 개념
-
선형회귀 원리 확장하기
- 일반선형모형: 설명변수가 양적변수인 다중회귀부터 설명변수가 범주형 변수인 분산분석까지를 포괄하는 선형모형
- 일반화선형모형(GLM): 일반선형모형 원리를 확장하여 최소제곱법이 아닌 확률분포에 기반한 최대가능도 방법으로 회귀모형을 추정
- 통계 모형화: 데이터 성질을 고려하면서 확률 모형을 가정하고 파라미터를 추정하여 모형을 평가하는 일련의 작업
-
가능도와 최대가능도 방법
'확률적으로 얼마나 나타나기 쉬운가'- 가능도
- 가능도가 크다 = 파라미터에서 얻은 데이터가 나타나기 쉽다
- 최대가능도 방법(추정): 가능도를 최대화하는 파라미터를 찾아서 이를 추정값으로 삼으면 얻은 데이터에 가장 잘 들어맞는 파라미터를 정할 수 있다
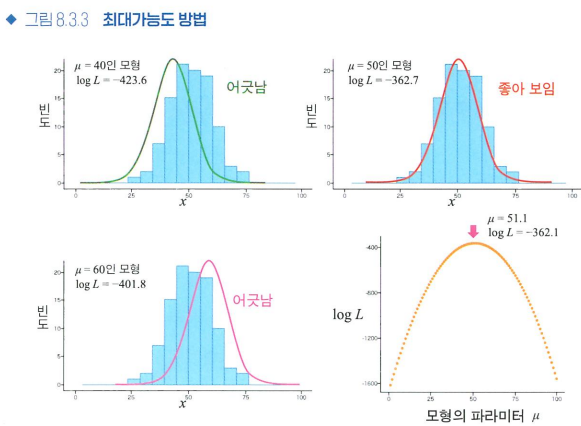
- 가능도
-
로지스틱 회귀
-
일반화선형모형의 일종
-
범주 하나가 일어날 확률을 p로 두고, 설명변수 x가 바뀌었을 때 p가 얼마나 달라지는지를 조사
-
p는 이항분포
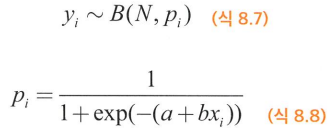
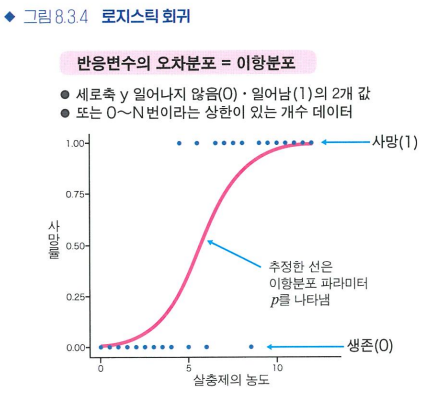
-
로지스틱 함수
-
f(x)
-정의역: 무한, 치역: [0,1]
-a: 평행이동, b: 변화정도 -
로짓 함수: 아래 식의 우변
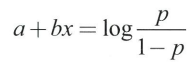
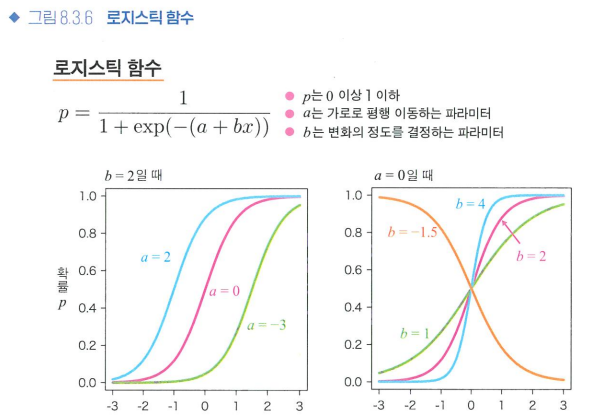
-
-
오즈비
- 오즈: 어떤 사건이 일어날 확률 p와 일어나지 않을 확률 1-p의 비율
p/1-p - 오즈비: 2개의 확률 p와 q에 대한 2개의 오즈 비율
OR = (p/(1-p))/(q/(1-q))
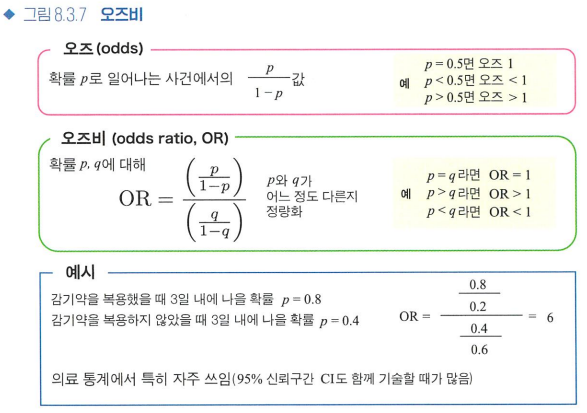
- 오즈: 어떤 사건이 일어날 확률 p와 일어나지 않을 확률 1-p의 비율
-
-
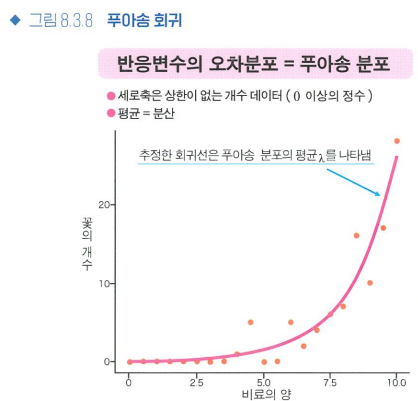
푸아송 회귀
- 푸아송 회귀: 데이터가 음수가 되지 않는 정수일 때, 특히 반응변수가 개수인 경우 고려해볼 수 있는 일반화선형모형
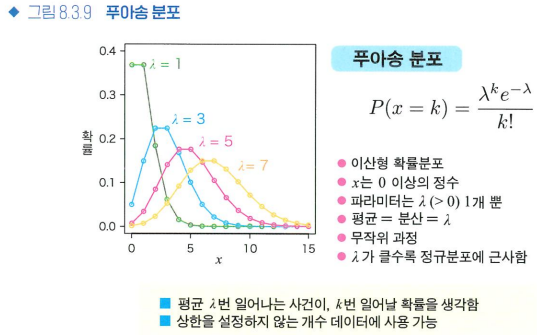
- 푸아송 분포: 낮은 확률로 일어나는 무작위 사건에 대해, 평균이 주어져있을 때 몇 번 일어나는지를 나타내는 확률분포