10장 인과와 상관

10.1 인과와 상관

• 인과관계 밝히기

  • 인과관계(복잡하게 구성된 네트워크)
  • 인과그래프: 원인과 결과를 원과 화살표로
    

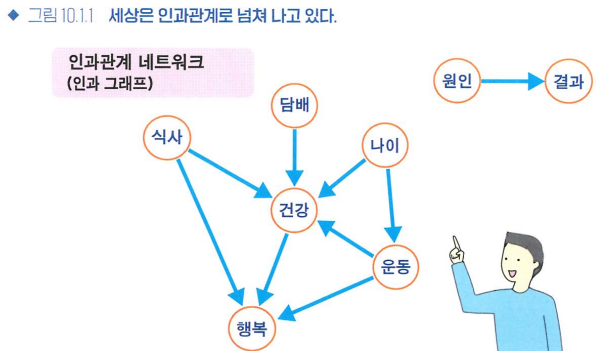
• 인과관계와 상관관계

  • 인과관계: 원인과 결과
  • 상관관계: 관련성
  • 중첩요인: 두 변수에 관련된 외부 변수가 존재할 때
    
    
  • 차이: 변수 간 관계의 방향성과 비대칭성
  • 실험연구와 관찰연구
    • 실험연구: 독립 변수(원인)를 조작하여 종속 변수(결과)에 미치는 영향을 분석하는 방식(인과관계)
      "무작위 통제 실험(RCT)"
    • 관찰연구: 변수 간 관계를 분석(상관관계)
      
      
  • 인과-상관-허위상관
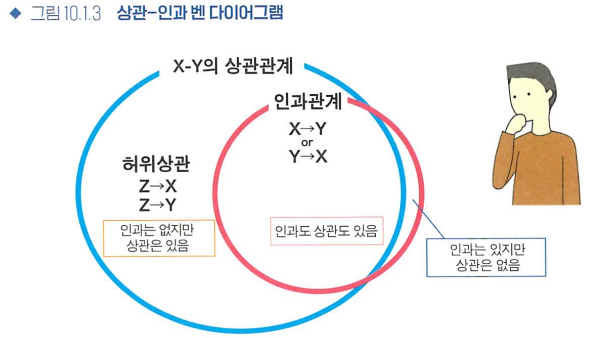
    • 허위상관: 인과관계는 없지만 상관관계는 있을 때
      
      
      
  • 인과관계, 상관관계를 알면 할 수 있는 일
    - 인과관계를 알 때: 원인 변수 개입 -> 결과 변수 변화 가능
    - 상관관계를 알 때: 한쪽 변수 -> 다른 변수 예측 가능
    
    

• 인간관계와 상관관계의 다양한 사례

  • 아이스크림 매출과 수영장 익사 사고: 여름철이라는 계절적 요인이 두 변수에 모두 영향을 미치기 때문에 상관관계가 나타난다. 두 변수 사이에 인과관계가 없다.
    "시간은 중첩요인이 되기 쉽다."
  • 초콜릿 소비량과 노벨상 수상자 수: 초콜릿 소비량이 많은 국가에서 노벨상 수상자가 많은 상관관계가 있지만, 이는 우연일 가능성이 크다. 이 상관관계를 인과관계로 오해하는 것은 오류이다.
    "우연히 생긴 상관"
  • GDP와 초콜릿 소비량: 초콜릿 소비량과 노벨상 수상자 수 간의 관계를 설명하기 위해, GDP가 중첩 요인일 수 있다.
    
    

10.2 무작위 통제 실험

• 인과관계를 밝히려면
  -> 밝히기 어려운 이유: 중첩요인의 존재
  
  
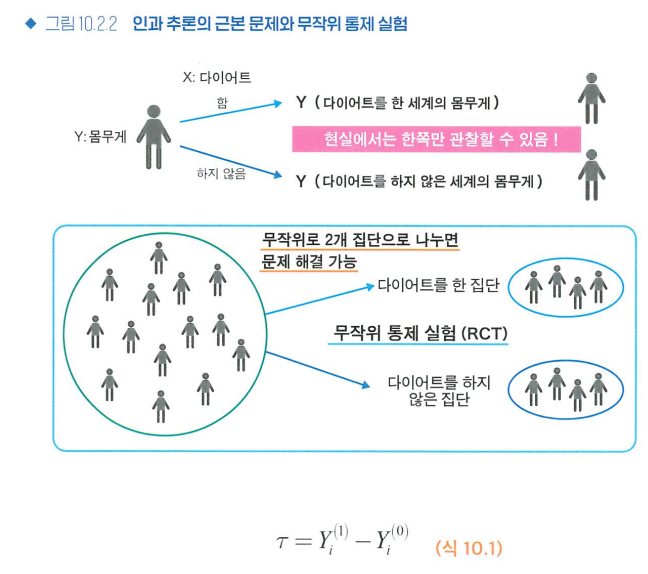
• 무작위 통제 실험(RCT)
  • X-> Y; 인과효과를 추정하는 가장 강력한 방법
  • X에 표본을 무작위로 할당하고 개입 실험을 수행한 다음, Y와 비교
  • 중첩요인을 확인하지 않더라도, 그 효과를 무작위를 이용하여 무효화할 수 있으므로, 알고자 하는 변수의 효과만 추정 가능하다.
    
    
  • 통계학에서의 인과관계
    수학적 기호를 사용하여 인과관계를 정의하고, 실제 데이터를 바탕으로 인과효과를 추정할 때 사용하는 기법들
    ex) E[Y(1)−Y(0)]는 다이어트를 했을 때와 하지 않았을 때의 체중 차이를 나타내는 기대값
    
    
  • 선택편향
    - 관측 가능한 기댓값은 원래 알고자 하는 효과에 편향이 더해진 값이 된다
    - 실험 대상자가 특정한 특성을 가질 가능성이 높을 때 발생
    - 중첩요인의 존재가 선택편향을 발생
    ex) 다이어트를 원하는 사람들은 평소 체중에 대해 더 관심을 가질 수 있기 때문에 체중 변화에 민감
    
    

10.3 통계적 인과 추론

• 인과효과를 추정하는 또 다른 방법
  무작위로 인한 한계 때문에 RCT사용이 힘든 경우 통계적 인과 추론
  
  
  • 다중회귀
    • y = a + b1_x + b2__z
    • 원인변수: 설명변수 x, 결과변수: 반응변수 y
    • 다중회귀 분석을 통해 중첩 요인 z의 영향을 통제하고 x의 인과효과를 추정
      
      
  • 층별 해석
    중첩요인을 기준으로 데이터를 층으로 나누어, 각 층 안에서 중첩요인의 효과를 가능한 한 작게 하는 방법
    
    
  • 경향 점수 짝짓기
    • 원인변수=0인 집단과 원인변수=1인 집단에서 비슷한 중첩요인을 가진 데이터를 골라 쌍으로 만드는 방법
    • 효과 = Y(0) - Y(1)
      
      
  • 이중차분법
    • 시간 축을 도입, 집단 간 차이에 대해 다시 한번 처리 전후의 차분을 취하는 방법
    • 효과 = (A2-B2)-(A1-B1)/ 처리 집단(A)과 대조 집단(B)
      
      

11장 베이즈 통계

11.1 베이즈 통계의 사고방식

• 통계학의 2가지 흐름

  • 기존의 통계 방법은 빈도주의 통계: 데이터의 반복적인 실험 결과를 바탕으로 확률 계산
  • 베이즈 통계: 사전 지식을 반영하여 불확실성을 다루며, 데이터가 관찰됨에 따라 확률이 갱신되는 방식으로 접근
    
    
  • 불확실성 다루기
    • 빈도주의 흐름에서의 불확실성: 모집단에서 표본을 추출할 때
    • 빈도주의 통계는 확률을 반복 실험의 결과로 보는 반면, 베이즈 통계는 확률을 불확실성을 표현하는 방법("얼마나 확신하는지")으로 사용
      

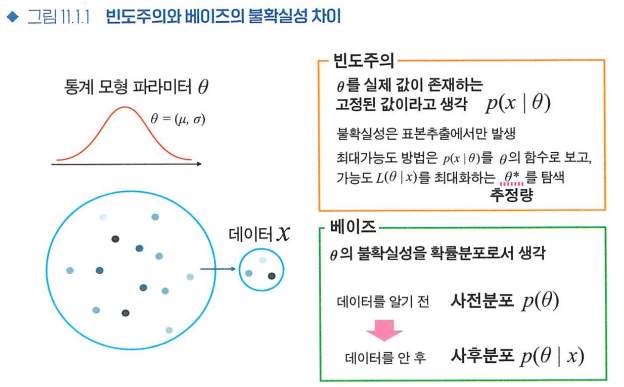
• 베이즈 통계의 이미지
  

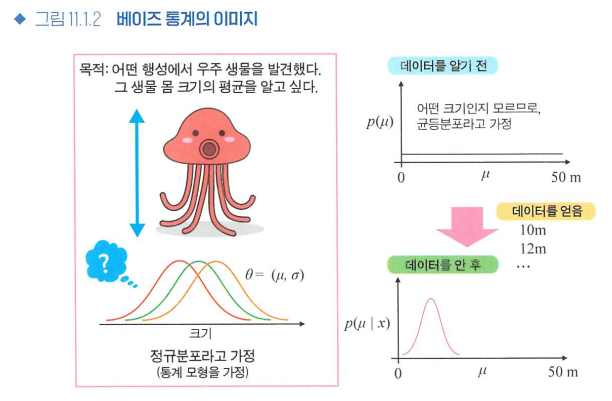
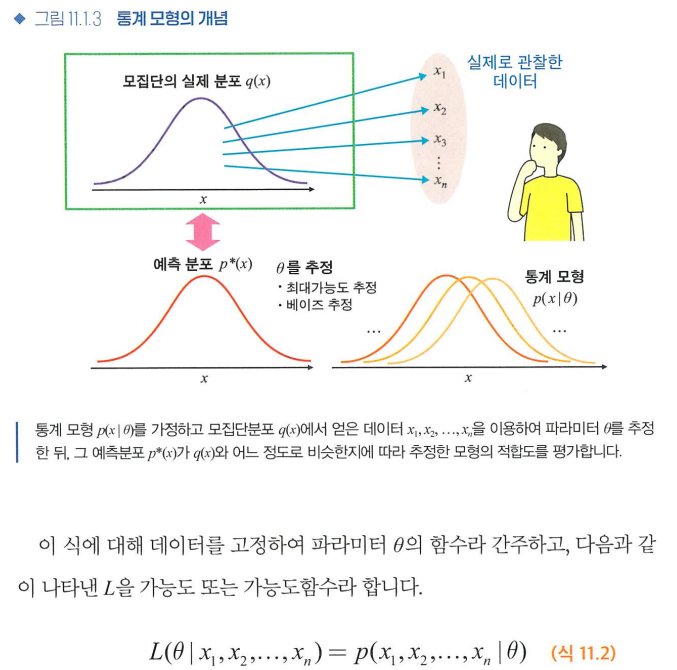
• 통계 모형

  • 통계 모형의 목적은 데이터의 발생원인 모집단의 실제 분포 q(x)를 아는 것
  • q(x)를 추론하는 것을 통계적 추론이라고 한다
  • 통계 모형 p(x)가 q(x)와 어느 정도 들어맞는지를 정량화함으로써 통계 모형 p*(x)의 적합도를 평가할 수 있다
    
    
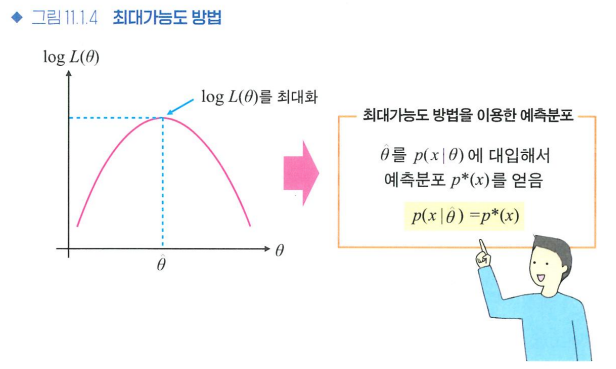
  • 최대가능도 방법
    - 특정 모수값이 데이터에 가장 적합할 확률을 찾는 방식, 베이즈 추론에서도 MLE 방법을 사용하여 예측분포를 결정한다
    
    
    

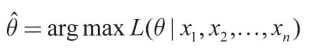
• 베이즈 통계의 사고방식
  통계 모형의 파라미터θ를 확률변수로 취급하여, 그 확률분포를 생각한다

  • 사전분포: 데이터 관찰 전, θ 확률 분포

  • 사후분포: 데이터 관찰 후, θ 확률 분포

    $p(\theta | x) = \frac{p(x | \theta) \cdot p(\theta)}{p(x)}$

  • 사후 분호는 가능도 X 사전분포에 비례하다
    
    

• 베이즈 추정의 방법론

  • 사전분포: 데이터를 얻기전에 파라미터가 어떤 분포인가를 미리 설정해야 하는 분포

    • 베이즈 추정에서 균등분포를 무정보 사전분포로서 이용하곤 한다
      -> 균등분포: 모든 값이 같은 정도로 발생하는 분포
      
      

  • 예측분포: 사후분포p(x)로 예측분포p*(x)를 만들 수 있다
    

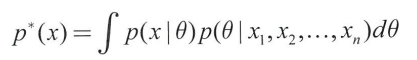
  • 정보량 기준
    실제 모집단 q(x)와 예측 분포 p*(x)가 어느 정도 일치하는가

    • 쿨백-라이블러 발산(KL divergence)
      
      
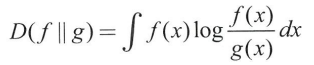
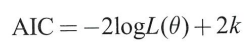
      AIC와 같은 모형의 좋고 나쁨을 평가하는 지표
      
      

• 베이즈 통계 이점

  • 장점
    불확실성이 높은 상황에서 유연하게 확률을 갱신할 수 있다.
    기존의 사전 지식을 통합하여 더 신뢰할 수 있는 예측을 도출할 수 있다.
  • 한계
    사전분포의 선택에 따라 결과가 크게 달라질 수 있으며, 일부 경우 주관적 판단이 개입될 수 있다.
    계산이 복잡하여 많은 경우 MCMC(Markov Chain Monte Carlo)와 같은 복잡한 계산 방법이 필요하다.

11.2 베이즈 통계 알고리즘

• MCMC 방법
  • 특정 확률분포를 따르는 난수 발생 알고리즘
  • 사후 분포를 따르는 난수를 발생시키고, 그 난수의 집합을 관찰함으로써 사후분포의 성질을 분석
    
    
  • 몬테카를로 방법
    • 난수를 반복 생성하여 근사해를 구하는 방식
      ex) 원의 넓이를 구하기 위해 좌표평면에서 여러 난수를 발생시키고, 난수 중 원 내부에 속하는 비율을 통해 넓이를 추정할 수 있다
      
      
  • 마르코프 연쇄
    - 현재 상태만을 고려하여 다음 상태로 전이하는 방식
    - 특정 조건에서 다른 상태로 이동하며 확률을 계산하는 방식으로, 현재 상황에 따라 변화하는 확률의 일종의 일정을 표현
    
    
• MCMC 방법의 예
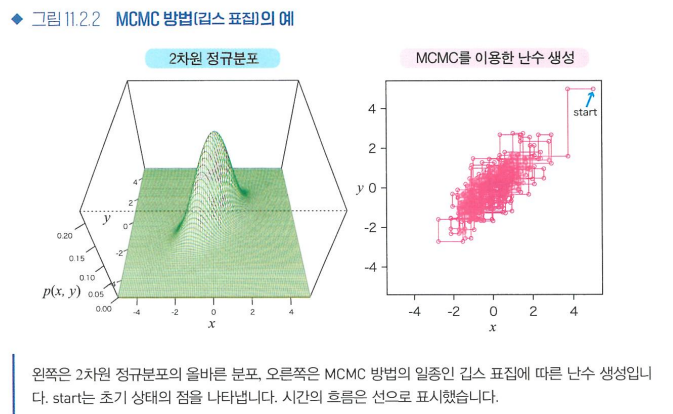
  • 깁스표집: 한쪽 변수를 고정한 뒤, 고정하지 않은 변수를 확률적으로 움직이는 작업을 번갈아 반복하는 순서로 이루어진다
    
    
    

11.3 베이즈 통계 사례

• 이표본 평균값 비교
  ex) 고혈압 환자 20명을 두 그룹으로 나누어 한 그룹에 신약을, 다른 그룹에 위약을 투여한 후, 혈압 변화를 측정하여 신약의 효과를 평가
  • 기존의 t-검정을 사용하는 가설 검정 대신, 베이즈 통계를 활용하여 분석
  • 이표본 평균값 비교: 신약 집단의 평균 혈압은 130.7, 위약 집단은 152.1로 나타났으며, 베이즈 분석을 통해 신뢰 구간과 사후확률을 제공
  • MCMC 방법 결과: 평균 차이의 사후분포가 안정화되는 과정, 체인이 안정적
  • 사후추정값
    • 점 추정: 사후기댓값(EAP), 사후최빈값(MAP)
    • 폭 추정: (1-a)% 신뢰구간, 확신구간(CI)
      
      
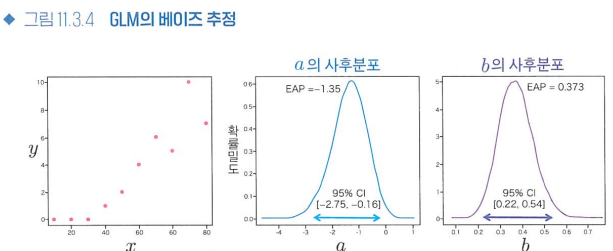
• 푸아송 회귀의 예
  • 푸아송 회귀를 통해 일반화 선형 모형(GLM)의 매개변수를 베이즈 추정으로 분석하는 예시
  • 파라미터 a와 b의 사후분포를 추정하여, 각 파라미터에 대한 신뢰 구간과 추정값을 제공
    
    
    
• 계층적 베이지안 모형
  • 사전분포의 분산을 추가적으로 조정할 수 있는 파라미터를 도입하여, 더 유연한 모델링을 가능하게 한다
  • 개체 간의 차이를 반영하여 사전분포의 분산을 조정하는 초모수 s를 추가하여 모형의 적합성을 높인다