4장 추론통계~신뢰구간
4.1 추론통계를 배우기 전에
-
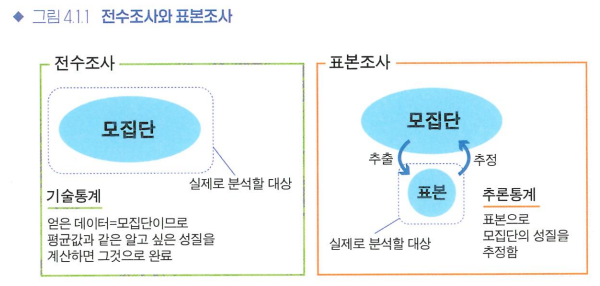
전수조사와 표본조사
- 전수조사: 모집단의 모든 요소를 조사
- 표본조사: 모집단의 일부인 표본으로 모집단의 성질을 추정
-
데이터를 얻는다는 것
"데이터(표본)을 얻는다는 것은 무엇인가?"
-
모집단분포: 모집단을 나타내는 분포, 전체 분포에서 일부를 추출한 것
- 모집단 관련 용어: 모평균, 모분산(모집단분포가 양적 변수의 분포일 때 정의 가능)/ 모수, 파라미터(모집단분포를 특징 짓는 양) -> 모수를 아는 것이 목표!
- 모집단에 포함된 요소 개수인 '모수'와 헷갈리지 말 것!
-
확률분포와 실현값
- 확률분포를 알고 있으면 실현값이 확률적으로 어떻게 움직일지를 이해할 수 있음
- 단, 실현값은 확률분포로부터 독립적으로 발생한다고 간주
- (확률분포, 실현값)의 관계는 (모집단, 표본)의 관계와 유사
- '모집단 = 확률분포', '표본 = 확률분포를 따르는 실현값'
-
-
데이터로부터 그 발생원의 확률분포 추정하기
"얻은 표본으로 모집단을 추정한다." = "얻은 실현값으로 이 값을 발생시킨 확률분포를 추정한다."
- 모형화: 수학적인 확률분포로 모집단분포를 근사하는 것
- 무작위추출: 데이터를 얻을 때 모집단에 포함된 요소를 하나씩 무작위로 선택하여 추출
- 단순무작위추출법: 표본에 있을 수 있는 모든 요소를 목록으로 만들고, 난수를 이용하여 표본 정하기
- 층화추출법(자주 사용됨): 모집단을 몇 개의 층(집단)으로 미리 나눈 뒤, 각 층에서 필요한 수의 조사대상을 무작위로 추출
- 편향된 추출로는 올바른 추정이 어려움
-
모집단에 대해 추정한 결과의 일반화는 도메인 지식에 따라 달라진다.
-
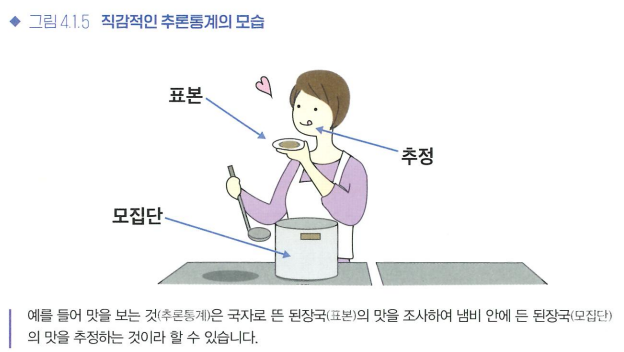
추론통계를 직감적으로 이해하기
4.2 표본오차와 신뢰구간
-
알고 싶은 값: 모집단평균(고정값) -> 표본에서 모집단평균 추정(확률적으로 변함)
-> 일반적으로 오차 발생: 표본오차
-
표본오차
표본오차는 확률적으로 바뀐다.- 큰 수의 법칙: 표본크기 n이 커질 수록 표본평균이 모집단평균에 한없이 가까워진다.
- 큰 수의 법칙: 표본크기 n이 커질 수록 표본평균이 모집단평균에 한없이 가까워진다.
-
표본오차의 확률분포
표본평균도 확률 변수 -> 표본오차의 확률분포를 알면 어느 정도의 크기의 오차가, 어느 정도의 확률로 나타나는지를 알 수 있다.
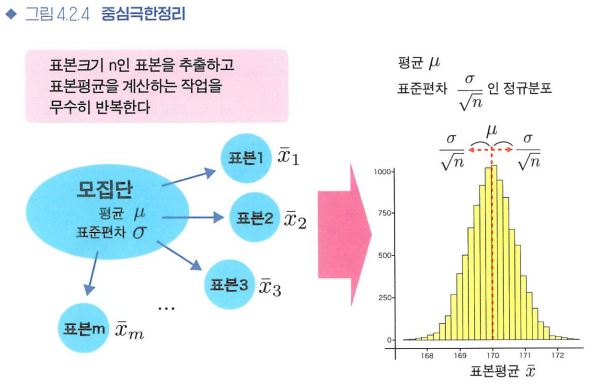
- 중심극한정리: 모집단이 어떤 분포이든 간에, 표본크기 n이 커질수록, 표본평균의 분포는 정규분포로 근사할 수 있다.
- 추정량: 모집단의 성질을 추정하는 데 사용하는 통계량
- 일치추정량: 표본크기 n을 무한대로 했을 때 모집단의 성질과 일치하는 추정량
- 비편향추정량: 추정량의 평균값(기댓값)이 모집단의 성질과 일치할 때의 추정량, 모집단의 성질을 과대하지도 과소하지도 않게 나타내는 양
- 표본오차의 분포
표본평균 x^의 분포 평균 = 모집단의 평균 m
표본오차 = x^-m의 분포는 평균 0 -> (근사) 평균=0 & 표준편차=σ/root(n)
표준오차 = σ/root(n)
- 중심극한정리: 모집단이 어떤 분포이든 간에, 표본크기 n이 커질수록, 표본평균의 분포는 정규분포로 근사할 수 있다.
-
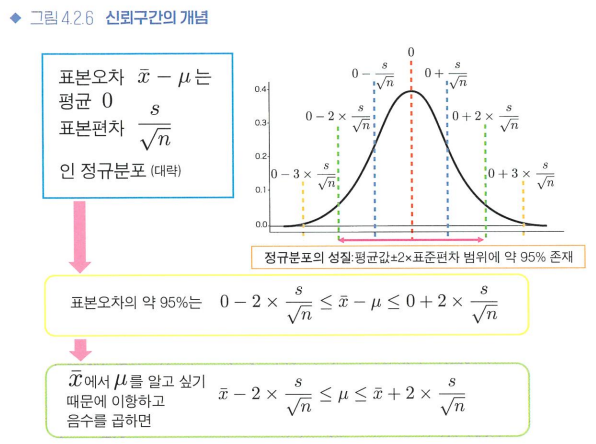
신뢰구간이란?
오차 정량화
" %의 확률로 이 구간에 모집단 평균이 있다."
-
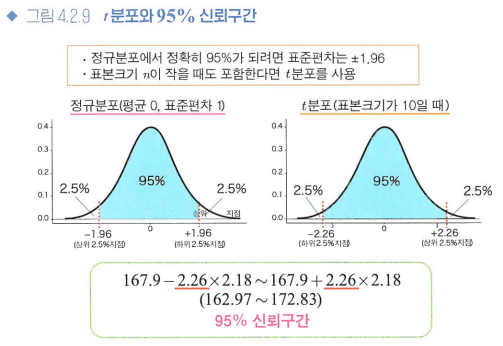
t분포와 95% 신뢰구간
- t분포: 모집단이 정규분포라는 가정하에 미지의 모집단 표준편차σ를 표본으로 계산한 비편향표준편차s로 대용했을 때, x^-m을 표준오차 s/root(n)으로 나누어 표준화한 값이 따르는 분포
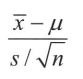
- 정밀도를 높이려면?
표준오차 s/root(n) -> s(비편향표준편차)를 작게 or n(표본크기)를 크게
- t분포 사용시 주의점
표본크기 n이 작아도 적용 가능한 t분포에는, '정규분포에서 얻은 데이터'라는 가정이 필요
정규분포와 현저히 다른 분포에서 데이터를 얻었을 때 주의!
단, n이 클 때는 중심극한 정리에 따라 표본평균을 정규분포로 근사할 수 있기 때문에 신뢰구간은 정확해짐
- 정밀도를 높이려면?
- t분포: 모집단이 정규분포라는 가정하에 미지의 모집단 표준편차σ를 표본으로 계산한 비편향표준편차s로 대용했을 때, x^-m을 표준오차 s/root(n)으로 나누어 표준화한 값이 따르는 분포
5장 가설검정
5.1 가설검정의 원리
-
가설검정
분석자가 세운 가설을 검증하기 위한 방법
p값을 계산하여 가설 지지 여부 판단
- 가설 검증
- 확증적 자료분석(가설검증형 데이터 분석): 미리 세운 가설을 검증하는 접근법
- 탐색적 자료분석: 가설을 미리 세우지 않고, 전체 데이터를 탐색적으로 해석하는 접근법
- 가설 검정
실험군/대조군 비교
- 가설 검증
-
통계학에서 가설이란?
밝히고자 하는 가설: "신약에 효과가 있다."
-> 신약 투여 모집단A, 위약 투여 모집단B / "두 모집단의 평균값이 서로 다르다."-
귀무가설: 밝히고자 하는 가설의 부정 명제(신약에 효과가 없다)
-
대립가설: 밝히고 싶은 가설(신약에 효과가 있다)
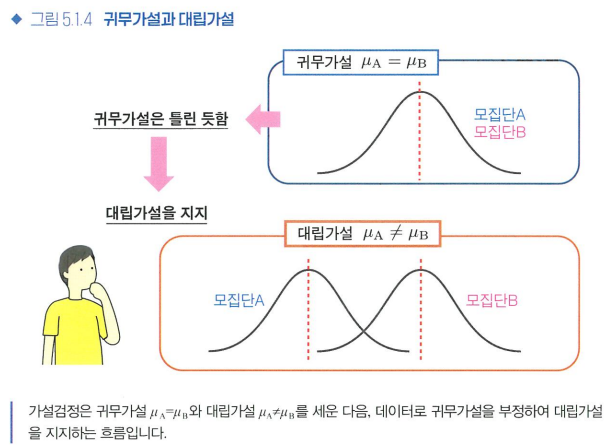
-
모집단과 표본의 관계
귀무가설이 옳다(모집단평균이 같다)고 해도 표본평균이 같지 않을 수 있다.(표본오차)
귀무가설이 옳다고 가정 -> 표본 추출 -> 표본평균의 차이를 히스토그램으로 -> t분포
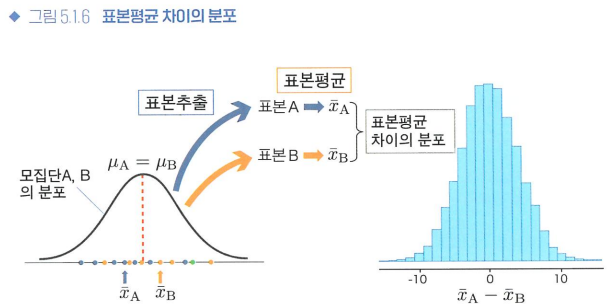
-
-
p값
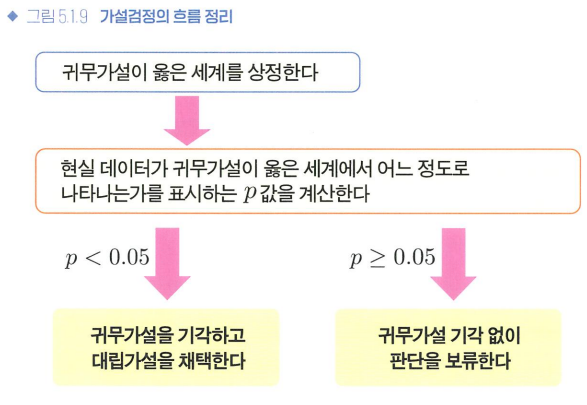
- p값: 현실에서 얻은 데이터가 귀무가설이 옳은 가상 세계에서는 얼마나 나타나기 쉬운가, 어려운가를 평가하고자 하는 확률
- 대립가설을 지지할 것인가?
- p<=0.05: 귀무가설 기각, 대립가설 채택 / "통계적으로 유의미한 차이가 있다."
- p >=0.05: 귀무가설 기각X / "통계적으로 유의미한 차이는 발견하지 못했다."
- 유의수준 α: 기각/채택의 판단 경계
-
가설검정 흐름 정리
5.2 가설검정 시행
-
가설검정 계산
- 이표본 t검정(어렵다...)
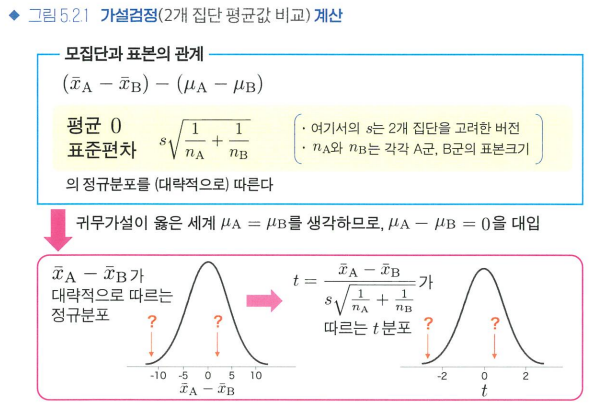
- 이표본 t검정(어렵다...)
-
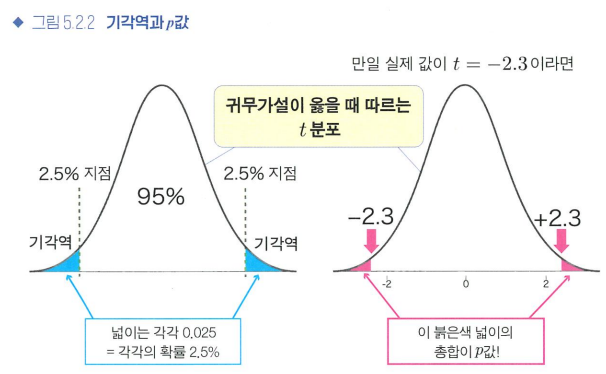
기각역과 p값
- 기각역: 분산분포의 좌우 2.5%씩의 영역, 유의수준 5%
- p값: 실제 값이 이 귀무가설이 옳을 때의 t분포 내 어디에 위치하는지 구한 뒤, 그 이상의 극단적인 값이 나올 확률을 구한 것
- 양측검정: 양수, 음수 모두 고려하는 가설검정 방법(보통 자주 쓰임)
단측검정: 한쪽만 고려해 넓이를 계산하는 방법
-
신뢰구간과 가설검정의 관계
- 신뢰구간: 실제 값인 표본평균으로 모집단 평균 추정
- 가설검정: 귀무가설을 가정해 모집단평균을 고정했을 때 표본평균이 어떤 값이 될 것인지를 구하는 것
5.3 가설검정 관련 그래프
- 오차 막대

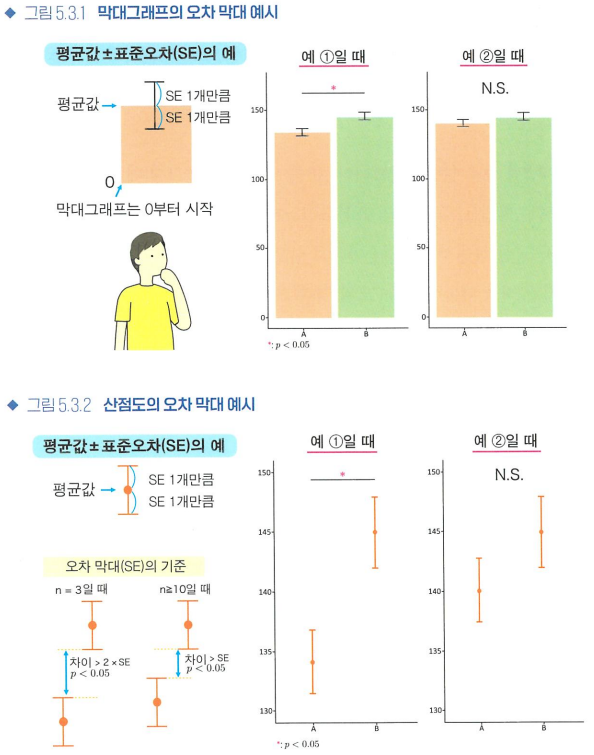
- SE: 표본크기 n에 따라 달라짐
표본크기가 작을 때는 오차 막대 2개(SE 2개)만큼의 차이가 있어야 p<0.05가 됨
표본크기가 클 때는, 오차 막대 1개만큼의 차이로도 p<0.05가 됨 - *: "통계적으로 유의미"
1개: p<0.05 / 2개: p<0.01 / 3개: p<0.001 / N.S.: 유의미하지 않다
- SE: 표본크기 n에 따라 달라짐
5.4 제1종 오류와 제2종 오류
- 진실과 판단의 4패턴
- 진실: 귀무가설 O, 대립가설 X / 귀무가설 X, 대립가설 O
- 판단: p값, 유의수준α와 비교 -> p<α(귀무 기각, 대립 채택) / p>=α(귀무가설을 기각할 수 없음)
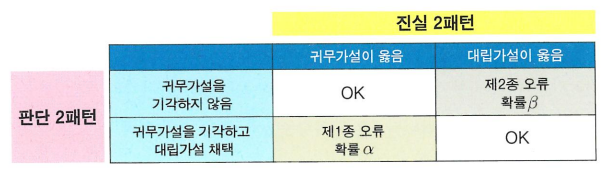

- 제1종 오류
실제로는 차이가 없지만 차이가 있다고 잘못 판단
유의수준 α값을 미리 정해두어, 제1종 오류가 일어날 확률을 통제할 수 있음
*α=0.05: 잘못이 20번 중 1번 정도 일어나는 위험을 허용한다
- 제2종 오류
실제로 차이가 있지만 차이가 있다고는 말할 수 없어, 귀무가설을 기각하지 않는 판단을 내리는 것
- 제2종 오류가 일어날 확률: β
- 검정력(제2종 오류가 일어나지 않는 확률): 1-β
- β는 n과 반비례 -> 1-β=80%가 이상적임
- α와 β는 상충관계
표본크기 n이 커지면, α를 고정한 상태에서 β가 줄어든다
-> n이 클수록 검정력(정말로 차이가 있을 때 그렇다고 판단할 확률) 1-β가 상승한다
- 효과크기를 달리 했을 때의 α와 β
- 효과크기: 일반적으로 얼마나 큰 효과가 있는지를 나타내는 지표
- 평균값의 차이에 비해 표준편차가 클수록 2개 분포의 겹치는 부분이 커지므로 효과크기 d는 작아지고 평균값의 차이는 검출하기 어려워짐
- α, β, n, d -> 3개를 알면 1개는 자동으로 정해진다
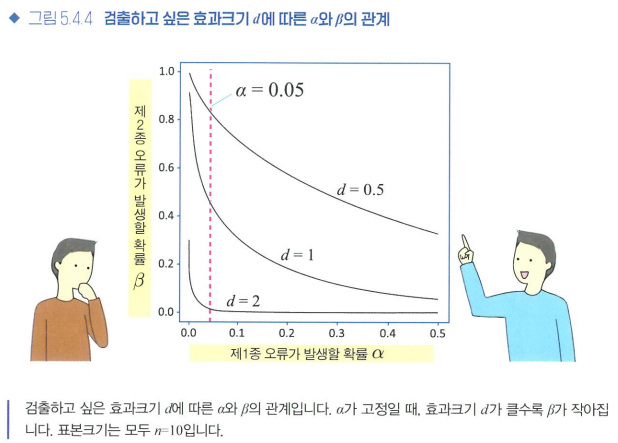
- 효과크기: 일반적으로 얼마나 큰 효과가 있는지를 나타내는 지표