1장 통계학이란?
1.1 데이터를 분석하다
"데이터 분석의 목적은 무엇인가?"
- 데이터를 요약하는 것
- 대상을 설명하는 것
- 설명에는 수준이 있다.- ex) 관계성
- 인과관계: 하나(원인) 변화 >> 다른 하나(결과)도 변화
- 상관관계: 한쪽이 크면 다른 한쪽도 큰 관계
- ex) 관계성
- 새로 얻을 데이터를 예측하는 것
: 기존 데이터를 기반으로 목적에 맞게 새로운 데이터 예측
1.2 통계학의 역할
데이터의 퍼짐을 설명하고 예측한다.
: 확률을 사용하자 = 확률론
1.3 통계학의 전체 모습
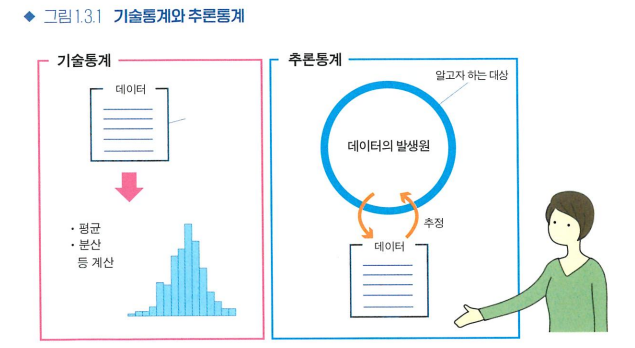
- 기술통계: 수집한 데이터를 정리하고 요약하는 방법, 데이터의 성질을 이해
- 추론통계: 수집한 데이터로부터 데이터의 발생원을 추정하는 방법
1) 통계적 추론: 데이터에서 가정한 확률 모형의 성질을 추정하는 방법
2) 가설검정: 세운 가설과 얻은 데이터가 얼마나 들어맞는지를 평가하여, 가설을 채택할 것인가를 판단하는 방법
다양한 분석 방법: 데이터 유형, 변수 개수, 가정하는 확률 모형 등에 따라 통계 분석 방법이 달라진다.
2장 모집단과 표본
2.1 데이터 분석의 목적과 알고자 하는 대상
데이터 분석 시작 단계: 목적 & 대상 정하기!!
2.2 모집단
- 모집단: 알고자 하는 대상 전체
'지금 알고자 하는 대상은 무엇인지' & '무엇을 모집단으로 설정할 것인지'- 모집단 크기에 따라 유한모집단/무한모집단
2.3 모집단의 성질을 알다
- 모집단의 성질을 아는 방법
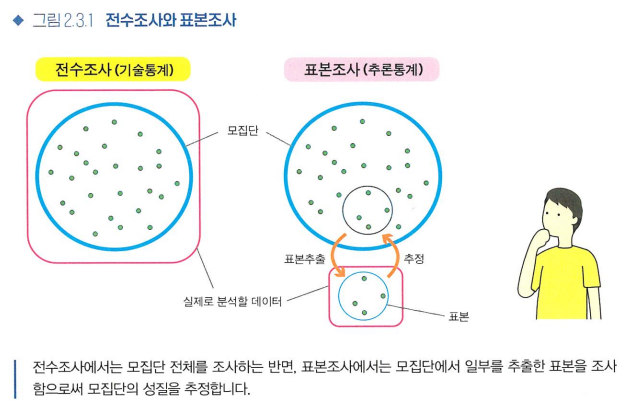
1) 전수조사- 모집단에 포함된 모든 요소를 조사
- 유한모집단일 때 가능
- 분석할 데이터 = 모집단
- 기술통계(데이터 그 자체의 특징을 기술 및 요약)
- 단점: 비용, 시간 부담 / 무한모집단의 경우 불가능
- 모집단의 일부(표본)를 뽑아서(표본추출) 분석하여 전체 성질을 추정(표본조사)
- 표본크기: 표본에 포함된 요소 개수 / ex. n=30: 30개의 표본 추출
3장 통계분석의 기초
3.1 데이터 유형
-
변수: 공통의 측정 방법으로 얻은 같은 성질의 값
- 1변수 -> 2변수 -> 3변수 -> ... -> 고차원 데이터 (>>> 변수 사이의 관계성 파악)
*변수의 개수 = 차원
- 1변수 -> 2변수 -> 3변수 -> ... -> 고차원 데이터 (>>> 변수 사이의 관계성 파악)
-
데이터 유형
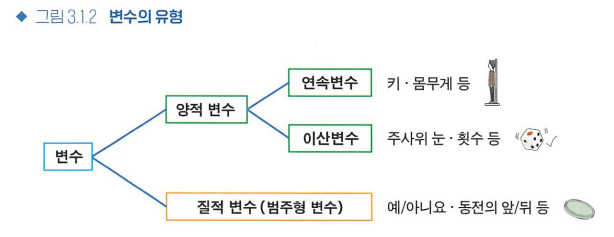
1) 양적 변수(수치형 변수)
- 이산형: 얻을 수 있는 값이 점점이 있는 변수, 셀 수 있는 숫자 데이터
- 연속형: 간격 없이 이어지는 값으로 나타낼 수 있는 변수
2) 질적 변수(범주형 변수)
- ex) 예/아니요, 앞/뒤, 식당 메뉴
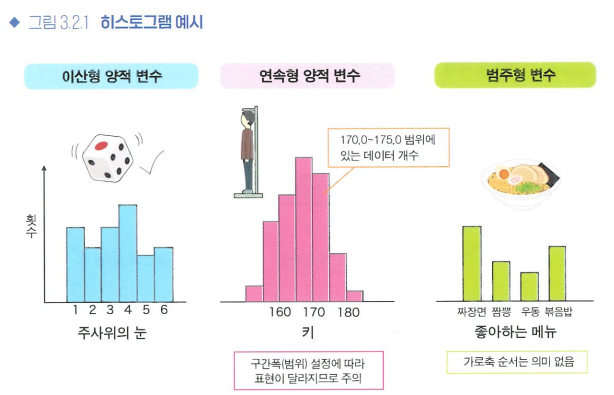
3.2 데이터 분포
- 데이터 경향 파악을 위한 시각화
3.3 통계량
-
데이터 그 자체의 성질을 기술하고 요약하는 통계량: 기술통계량, 요약통계량
-
대표적인 기술 통계량
1) 대푯값: 대략적인 분포 위치, 대표적인 값을 정량화
ex. 평균값, 중앙값, 최빈값
* 처음에 히스토그램을 그려 대략 파악 후에, 대푯값으로 적절한 분포를 특징 지을 수 있는지 확인2) 분산과 표준편차
- 표본분산: 표본의 각 값과 표본평균이 어느 정도 떨어져 있는지
s^2 = sum((x-x*)^2)/n
- 표본표준편차 = s
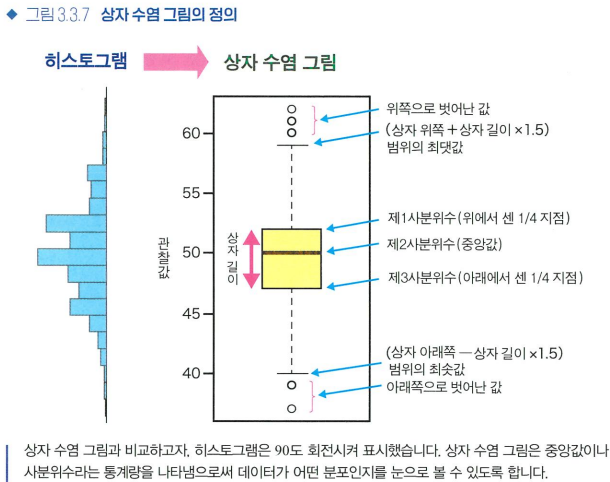
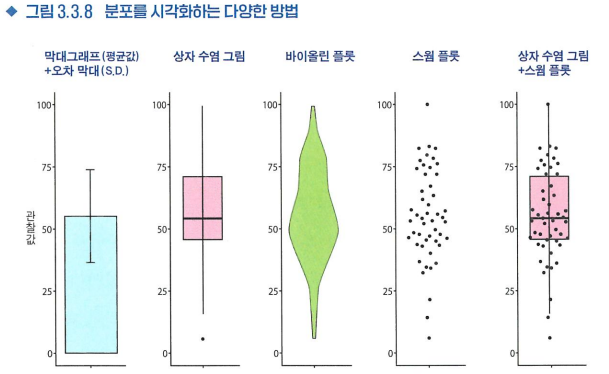
- 분산 확인하는 시각화 도구: 상자 수염 그림(통계량O / 상세한 분포 형태 X)-
이상값(평균값에서 표준편차의 2배 또는 3배 이상 벗어난 숫자) 주의
-
3.4 확률
- 확률: 불확실한 사건의 발생 가능성을 숫자로 표현한 것
- 확률 변수 X / ex) P(X=붉은 구슬) = 1/5
- 실현값: 확률변수가 실제로 취하는 값(붉은 구슬 or 흰 구슬)
- 확률 분포: x축 확률 변수, y축 확률 변수의 발생 가능성
- 확률밀도함수: 연속형 변수의 확률 계산 함수
'모집단과 표본 데이터' >> '확률분포와 그 실현값'
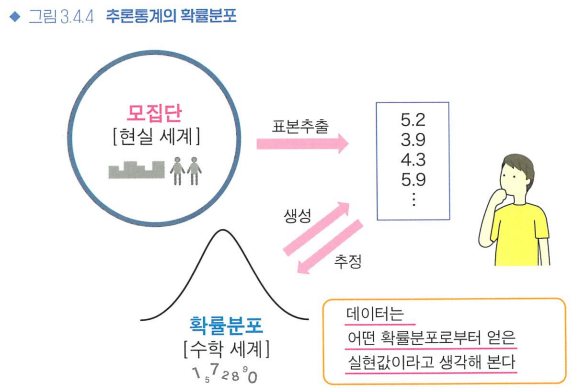
- 기댓값: 변수가 확률적으로 얼마나 발생하기 쉬운가를 평균적인 값으로 나타낸 값
- 분산과 표준편차
- 왜도: 분포가 좌우대칭에서 어느 정도 벗어났는지/ 첨도: 분포가 얼마나 뾰족한지, 그래프의 꼬리가 차지하는 비율이 얼마인지
- 동시확률분포 P(X, Y)
- 독립일 때 P(X, Y) = P(X) * P(Y) - 조건부 확률 P(X|Y) : Y의 정보가 주어졌을 때 X의 확률
3.5 이론적인 확률 분포
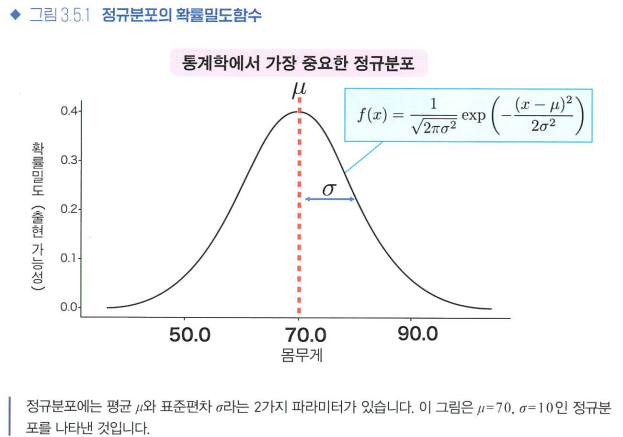
- 이론적인 확률 분포는 수식으로 표현되며, 분포의 형태를 정하는 숫자인 파라미터(모수)를 가진다.
- 정규 분포
N(μ, σ2)
표준정규분포 = N(0, 1)
- 표준화
평균 0, 표준편차 1로 변환
평균과의 거리가 표준편차의 몇 배인가를 나타내기 때문에 본래의 평균과 표준편차에 상관없이 분포 안에서 어디에 위치하는가를 알 수 있다.