2017년에 나온 Attention Is All You Need논문에 대해 공부한 내용 정리한 포스팅입니다.
잘못된 부분에 대한 의견 환영합니다 공부를 위해 댓글에 달아주시면 감사하겠습니다!!

논문 소개

기존 RNN기반의 sequential 방식에서 attention연산을 통한 parallel한 방법으로 구현되었다.
인코더-디코더의 구조로 되어있으며 인풋이 하나의 시퀀스로 여러개의 토큰들로 이루어져있다.
한 시퀀스가 인코더의 입력으로 들어가 아웃풋으로 나올때 토큰들이 병렬적으로 디코더에서 출력되므로 토큰들이 서로의 정보를 담고 있으며 이전의 모델보다 훨씬 더 좋은 성능을 낸다.

논문 요약

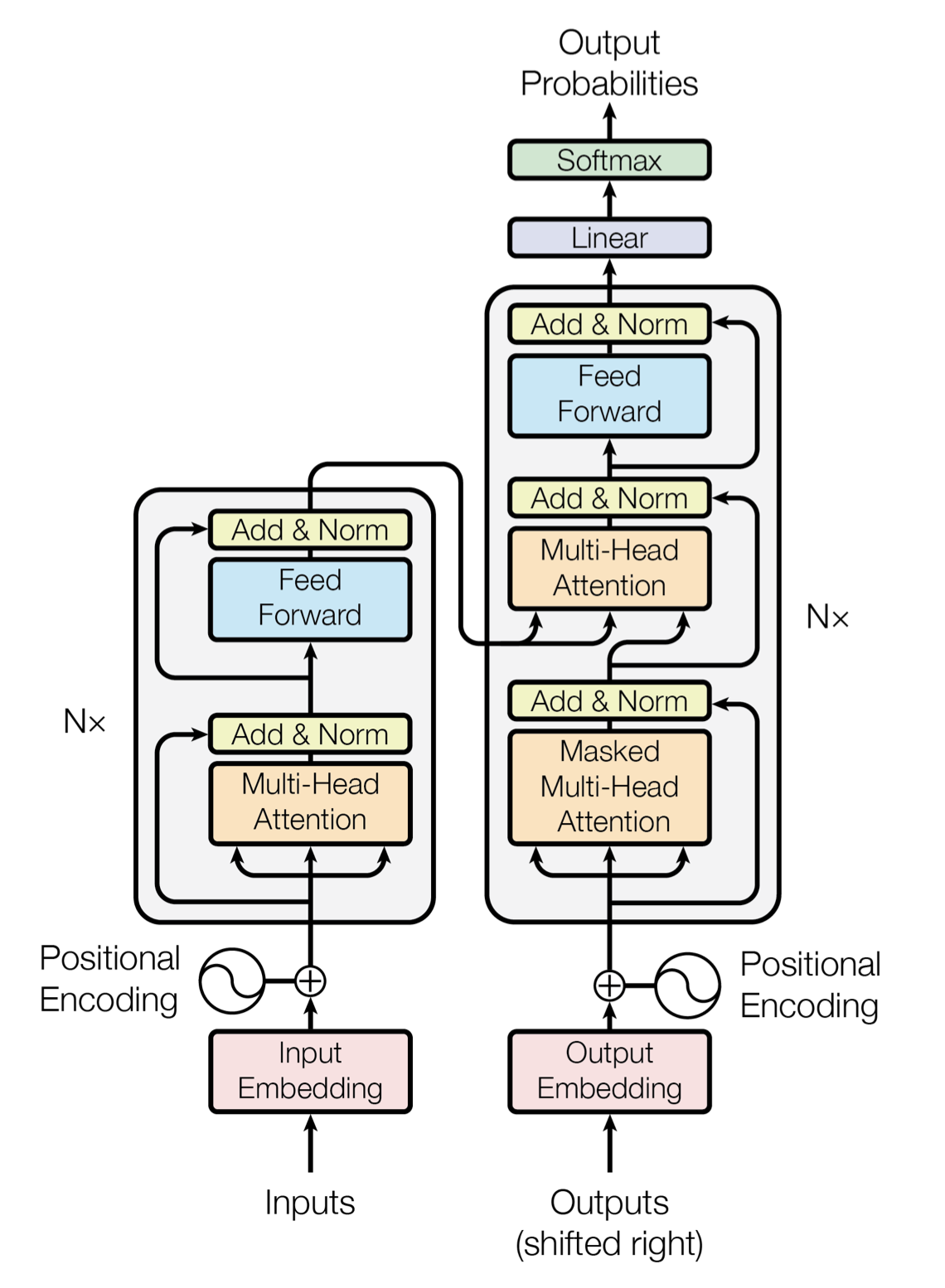
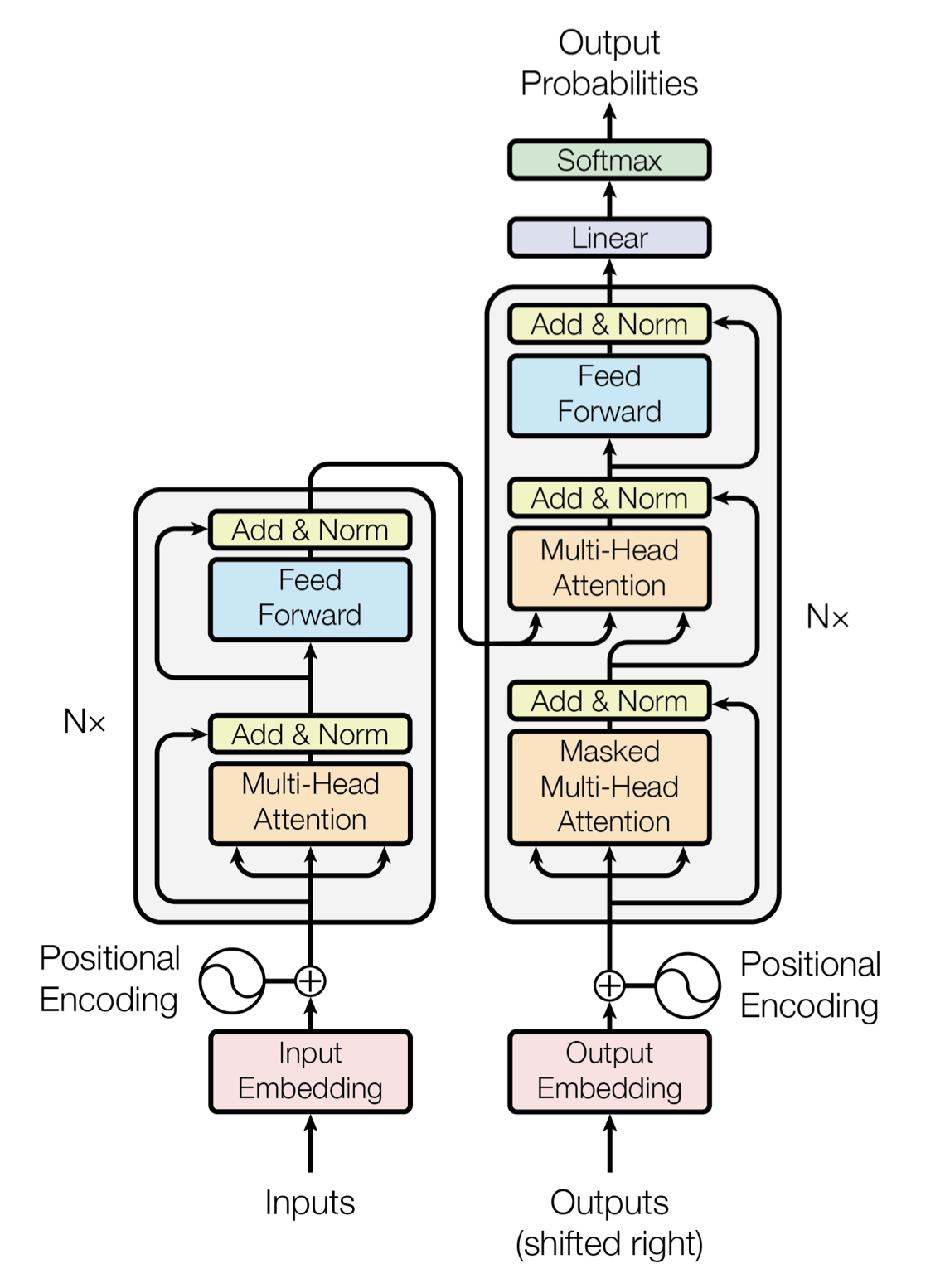
모델의 구조는 아래와 같다.

Positional Encoding

sequential한 RNN방식을 전혀 사용하지 않고 Attention만으로 구현을 했기 때문에 위치정보를 표현을 하기 위해 사용한다.
시퀀스 안에 단어간의 상대적인 위치정보를 입력하기 위해서 두개의 매개변수(단어의 번호 pos와 단어에대한 임베딩 위치 i)를 가지는 주기성을 가진 함수를 사용한다.
따라서 트랜스포머는 사인함수와 코사인 함수의 값을 임베딩 벡터에 더해줌으로서 단더의 순서정보를 더해준다.
함수가 다음과 같을때 (이때 sin이나 cos이나 성능의 차이는 크게 없다고 한다.) 인덱스가 짝수인 경우 사인함수를 이용하고 홀수인경우 코사인 함수를 이용한다.

$PE(pos,2i)=sin(pos/10000^{2i/d_{model}})$
$PE(pos,2i+1)=cos(pos/10000^{2i/d_{model}})$

임베딩 매트릭스는 nxd_model (n은 입력 시퀀스의 크기,즉 단어(토큰)의 개수)의 사이즈이며, 임베딩 매트릭스에서 인덱스값과 동일하게 (pos,i)로 접근할 수 있다.
따라서 input embedding을 이용해 위치인코딩 매트릭스를 만들어 더해주면 차원을 보존한 형태로 첫번째 인코더에 들어갈 입력이 완성된다.
여기서 주의할 점은 위치인코딩 함수가 두가지 성질을 가져야 하는데
첫째,모든 위치에서 인코딩 벡터의 norm크기는 같아야한다.
둘째,두 위치가 멀리 있을수록 거리도 커진다.

Encoder

Multi-Head Attention

이 레이어에서는 입력 시퀀스안에서 현재 단어가 다른 단어들과 어떤 연관성을 가지는지 알아보기 위한 연산을 한다. head의 개수는 하이퍼 파라미터로 본 논문에서는 multi-head attention을 통과한 벡터들을 concat했을때 기존 차원인 512dim이 되기 위해 8로 설정하였다. self-attention에서 head를 여러개로 정해주면 multi-head attention이 된다.

Self-Attention

self-attention연산을 위해 쿼리, 키, 값을 결정하기위한 매트릭스 $W^Q,W^K,W^V$ 3개를 학습시킨다.
이때 입력은 시퀀스로 한번에 들어가는게 아니라 토큰단위로 진행된다.

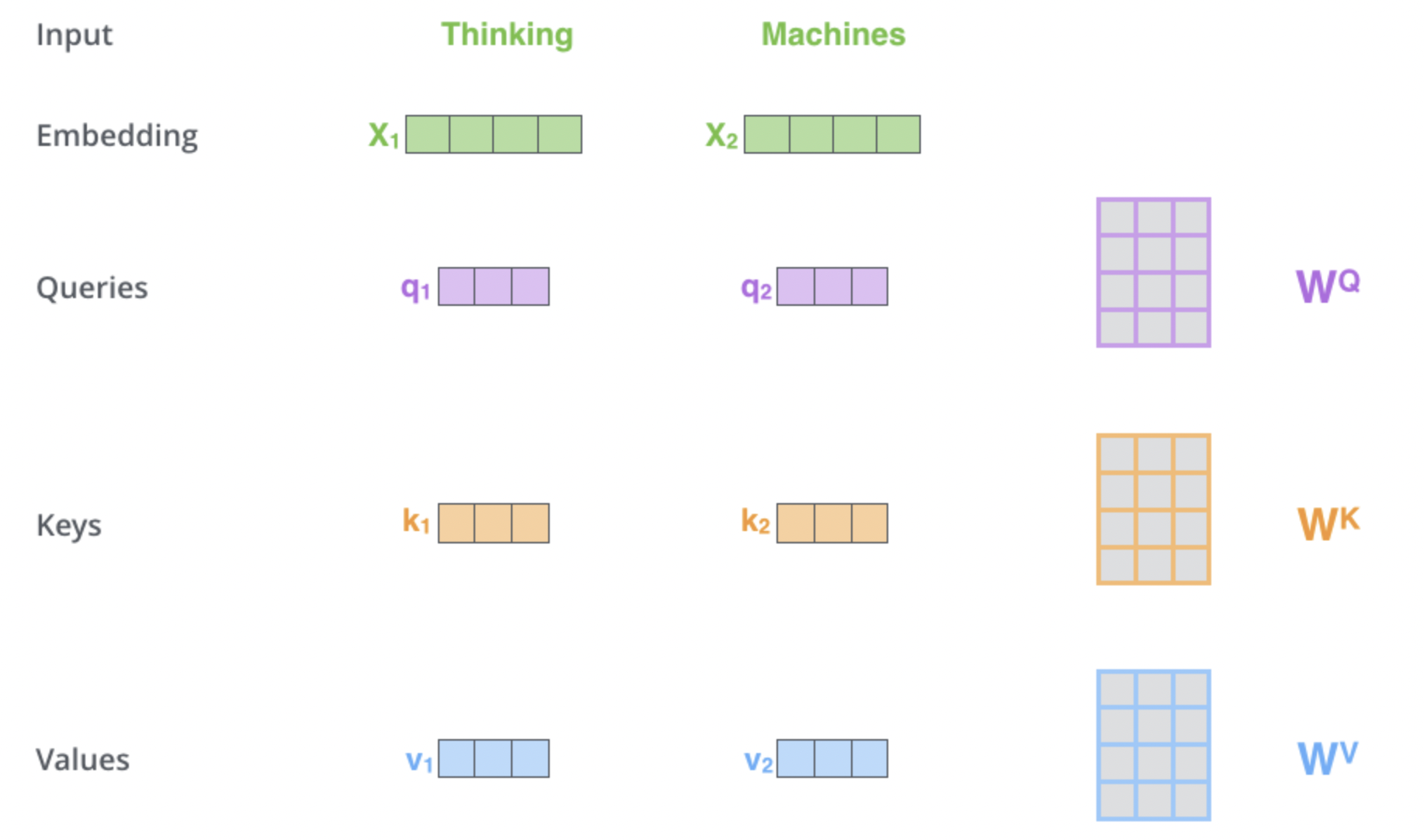
예를 들어 사진처럼 입력시퀀스는 Thinking Machines라고 해보면 Thinking과 Machines에 대해서 각각 임베딩 벡터인 $X_1,X_2$가 만들어지고, $W^Q,W^K,W^V$에 의해 각각 $q_1과 q_2, k_1과 k_2, v_1과 v_2$이 만들어진다.

한 시퀀스 안에서 각 단어가 다른 단어와 얼만큼의 연관성을 가지는지 알아보기 위해서 이 방법을 사용한다.
한 단어에대해 문장안의 모든 단어들과 연산을 해야한다.
현재 단어를 쿼리, 문장 내에서 다른 단어와의 연산을 위해 다른 단어를 가리키기 위한 키, 가리킨 키에 대해서 연산을 하기 위해 값을 사용한다.

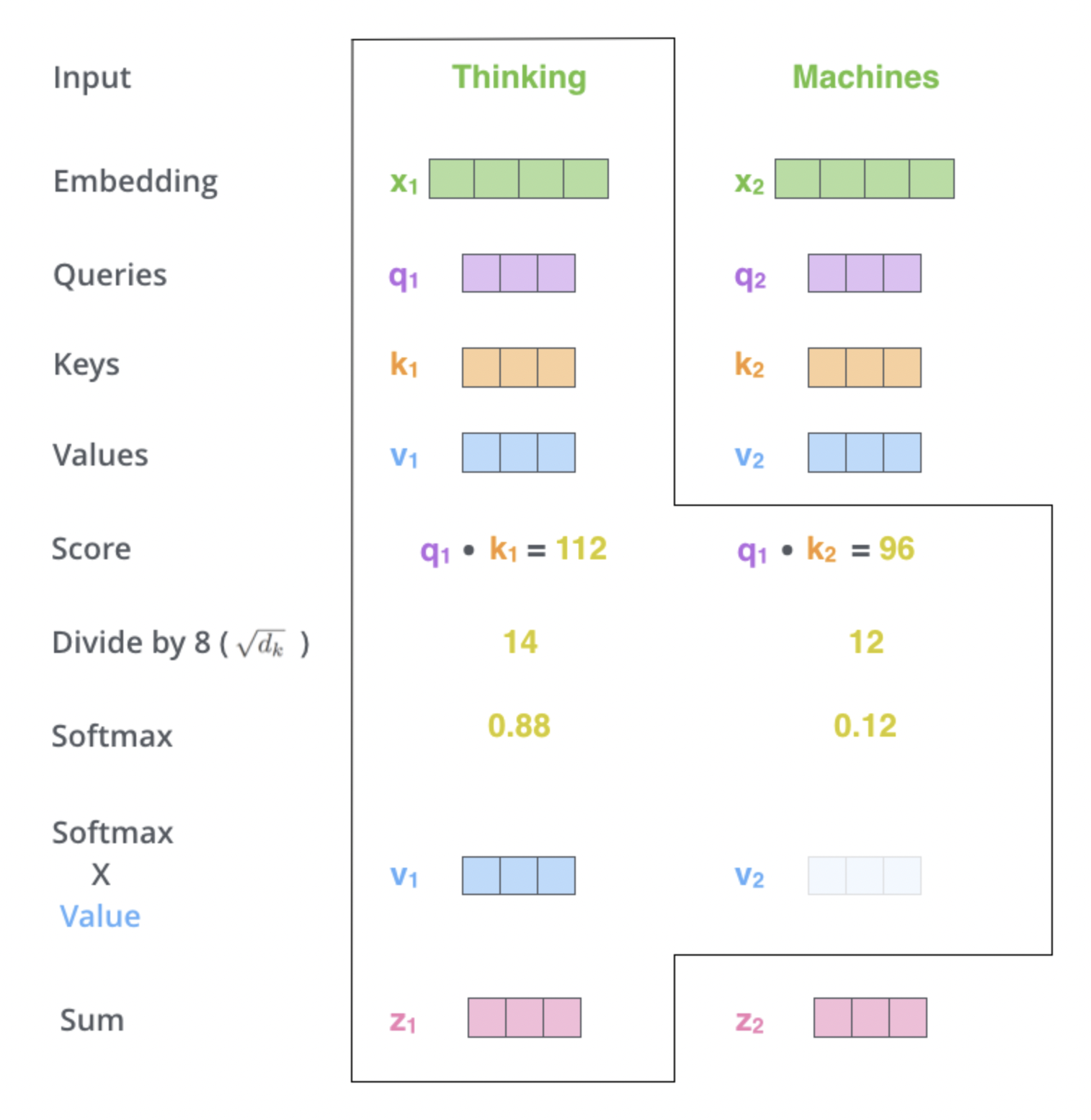
예를 들어 사진처럼 현재 단어가 Thinking이면 현재 단어인 $q_1$에 대해 모든단어들의 연관성을 알아보기 위해 자기자신을 포함해 문장안에 모든 단어들과 내적연산을 통해 score을 알 수 있다.
그리고 차원에 루트를 취한 값을 나눠주는데 이는 안정적인 그라디언트를 위해 한다.
그리고 소프트맥스를 통해 확률값으로 바꿔주고 이를 각 확률값에 대해 값과 곱해준뒤 합하면 $z_1$이 나온다.
즉, $Z_1$은 문장내에 모든 단어들에 대해 연관도에 따라 가중치를 부여한 값이 된다.
이제 이 연산을 모든 단어들에 대해 한번에 연산하기 위해 행렬을 이용해 다음과 같이 계산할 수 있다.

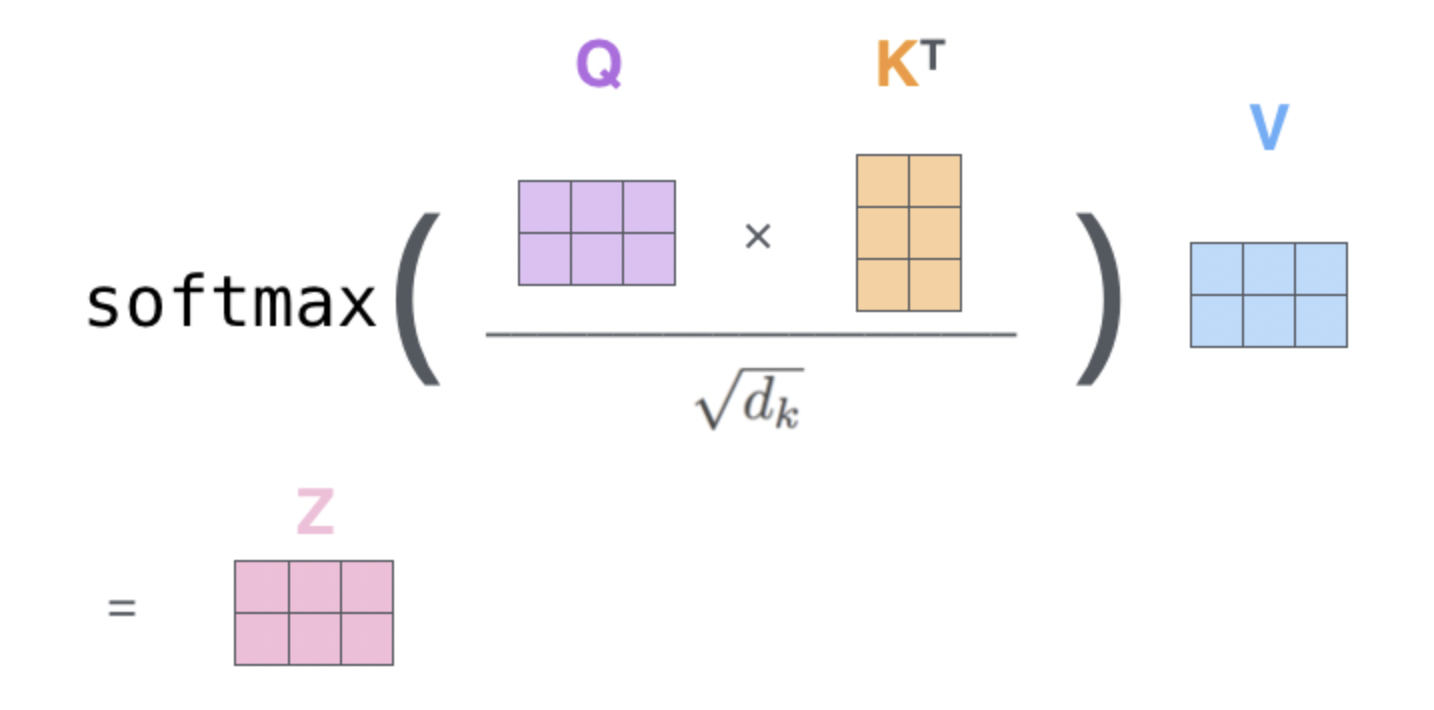
Multi-Head

이제 멀티헤드를 이용하는 이유는 서로 다른 부분공간에 있는 Representation추출이 가능하기 때문이다.
The animal didn't cross the street because it was too tired라는 문장이 있을때

5번째 레이어에서 it이 다른 head에서는 다른 부분에 더 초점을 맞추고 있다.
이렇게 헤드를 여러개 사용하면 다른 부분공간에서 추출이 가능하다.
여러개의 헤드를 통해 생성된 $Z_n$ 매트릭스들은 concat연산을 통해서 합친다. 그리고 또다른 가중치매트릭스인 $W^O$와 내적연산을 통해 원래 차원과 같게 만들어준다.

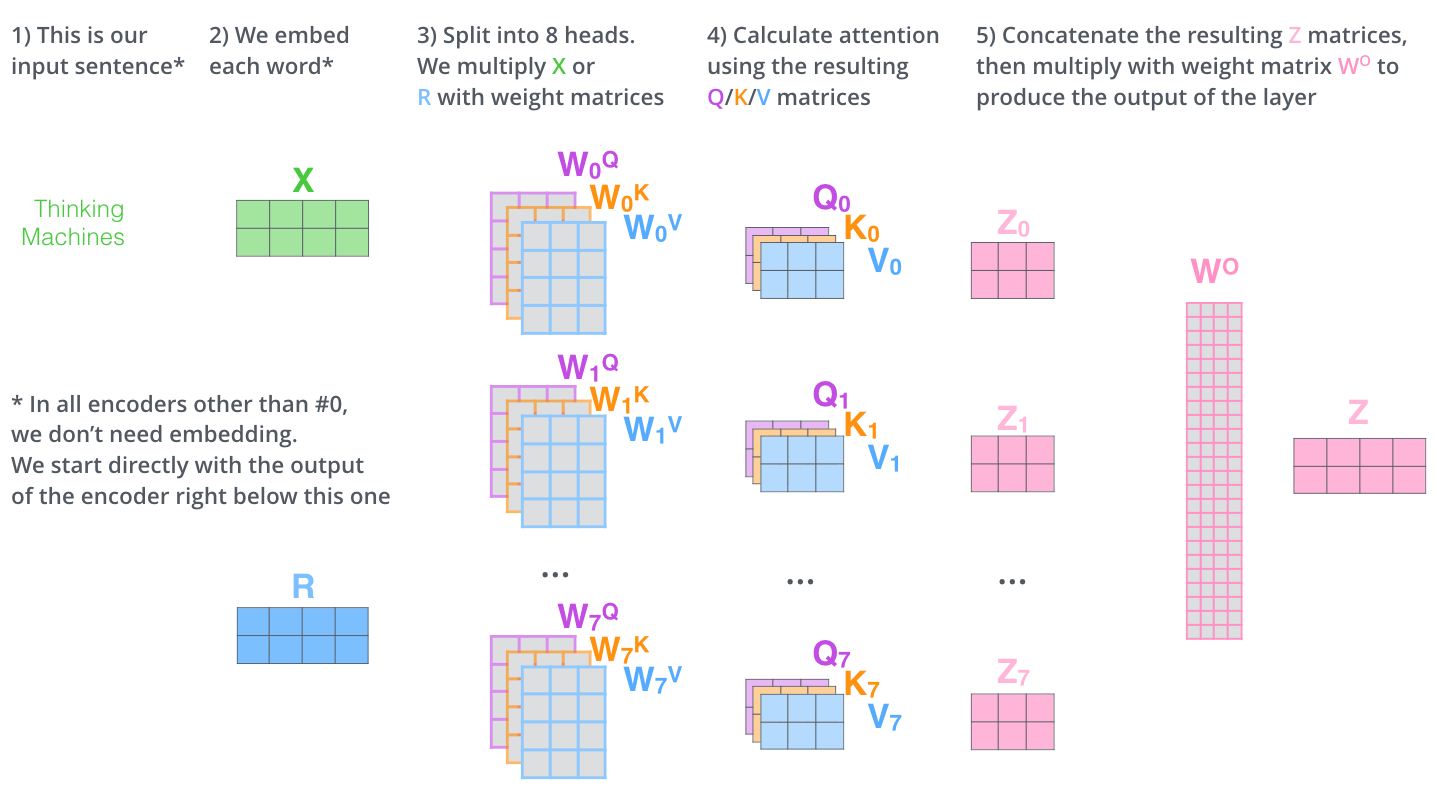
따라서 학습시켜야할 가중치 매트릭스는 head가 8개 일때 $W_i^Q,W_i^K,W_i^V$(i가 0~7까지)와 $W^O$로 총 25개이다.
첫번째 인코더에서는 인풋시퀀스 X를 그 다음 인코더부터는 이전 인코의 출력에서 나온R을 현재 인코더의 입력으로 사용하고 출력은 Z로 차원이 계속 보존되는것을 알 수 있다.

Position-wise Feed Forward

fully connected된 feed forward network이다. 각 입력별로 분리되게 동일한 연산이 적용된다. 이 레이어에서는 두번의 선형변환과 활성화 함수인 ReLU을 이용해 위치마다 개별적으로 적용되게 즉, position-wise한 연산을 한다.
$FFN(x)=max(0,xW_1+b_1)W_2+b_2$
선형변환을 통해 $xW_1+b_1$을 만들어 준후에
ReLu를 통해 $max(0,xW_1+b_1)$
선형변환을 한번더 진행해 최종적으로 $FFN(x)$가 만들어진다.

Add & Norm

Residual Learning으로 함수를 취한값뿐 아니라 현재 값을 함께 더해주는 방식이다.
vanishing gradient문제 해결을 위해 f(x)+x를 더해준다면 만약 미분시 f'(x)+1이 되어서 f'(x)값이 0이 되어도 적어도 1은 더해지기 때문이다.
그후 layer-normalization을 진행한다.

Decoder

Masked Multi-Head Attention

encoder에서는 한 시퀀스의 모든 단어들을 사용해 mask할 필요가 없었다. 하지만 decoder부분에서는 이전의 부분만 고려하기때문에 mask를 사용해 현재 단어와 이전 단어들간의 연관성만을 사용한다.
입력은 지금까지의 output을 임베딩을 거쳐 positional encoding을 한 후 사용한다.
encoder의 self-attention과 똑같이 진행되는데 masking을 적용하기위해 단어간의 연산시에 score를 -inf로 만들어준다. softmax값이 0이 되기때문에 weighted sum계산기 값이 반영되지 않는다.

Multi-Head Attention

encoder의 multi-head attention과 같은 연산이다. 쿼리는 디코더 안에 현재 단어를 의미하고 키와 값은 인코더에서 나온 값을 사용한다. 그러면 현재 단어에 대해 전체 시퀀스에서 인코더로 변환된 가중치 합을 사용한다.

Position-wise Feed Forward와 Add & Norm은 인코더와 같아서 생략한다.

final step

Linear

선형변환을 통해 fully-conencted NN가 vocal_size만큼의 벡터차원으로 변환시킨다.

Softmax

확률값으로 바꿔 그중 가장큰 단어를 선택한다.

전체적인 구조

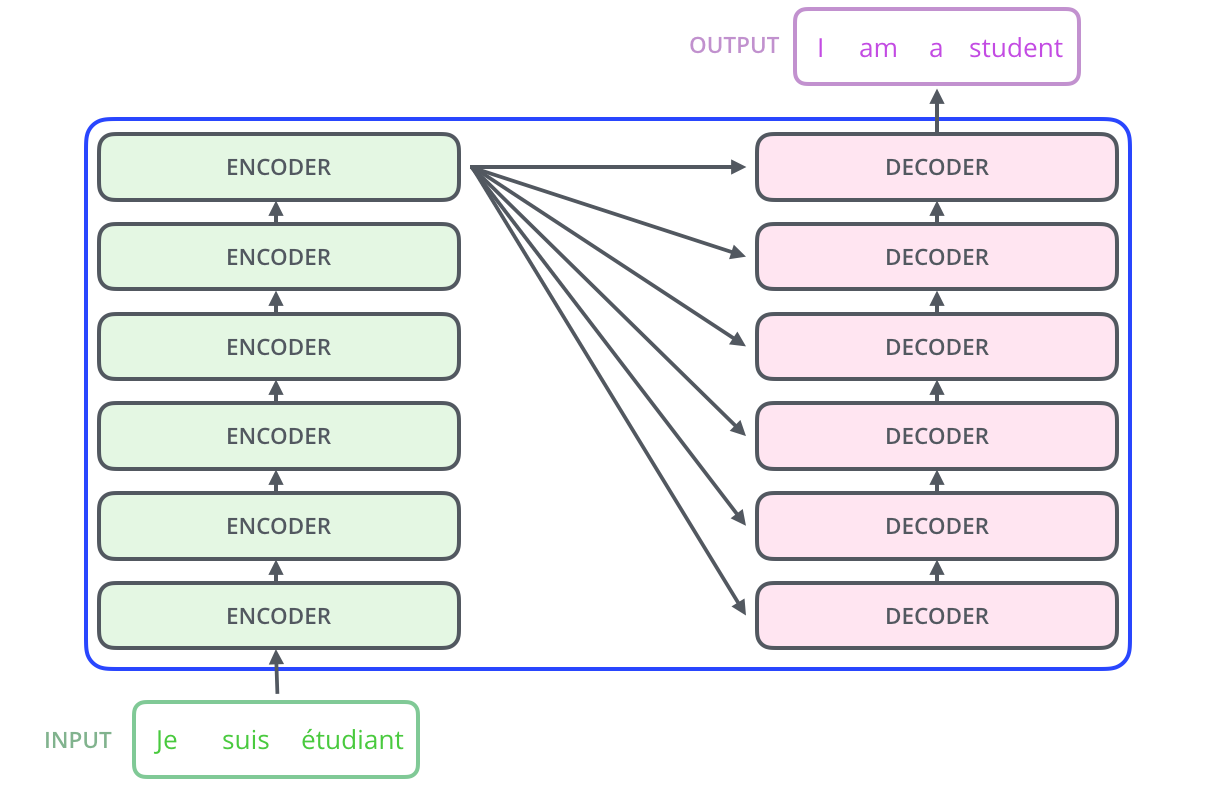
인코더의 마지막 부분이 모든 디코더에 관여를 한다. 본 논문에서는 인코더와 디코더를 6개씩 사용하였다.

참고

논문링크

https://arxiv.org/abs/1706.03762

논문요약부분

https://jalammar.github.io/illustrated-transformer/ (Jay Alammar 블로그)

개념공부

https://www.youtube.com/watch?v=AA621UofTUA (Youtube: 나동빈)
https://www.youtube.com/watch?v=Yk1tV_cXMMU&list=PLetSlH8YjIfVzHuSXtG4jAC2zbEAErXWm&index=17 (Youtube:
고려대학교 산업경영공학부 DSBA 연구실)