[Paper Review] Deep Knowledge Tracing (2015)

✅ 용어 정리

본 논문 리뷰에서는 다음과 같이 용어를 정리하여 사용합니다.

1. Interaction → 상호작용 또는 문제 풀이
2. Exercise → (학습) 활동

---

1 Introduction

✅ 심층 지식 추적 (Deep Knowledge Tracing, DKT)

📌 논문 시사점

1. 반복 신경망에 대한 입력으로 학생 상호 작용을 인코딩하는 새로운 방법
2. 지식 추적 벤치마크에서 이전 최고의 결과보다 AUC가 25% 상승
3. 지식 추적 모델에 전문가의 주석(annotation) 필요 X (전문가가 설정한 지식 구조나 개념 태그 없어도 문제 간 개념적 연관성이나 학생의 지식 상태 변화 추적 가능)
4. 학습 활동 영향력 발견 및 개선된 활동 커리큘럼 생성

✅ 지식 추적 (Knowledge Tracing)

• 시간이 지남에 따라 학생의 지식을 모델링하여 학생들이 미래 문제 풀이에서 어떻게 수행할지 정확하게 예측할 수 있도록 하는 작업
• 학생의 문제 풀이 기록을 바탕으로 다음에 풀 문제에서 정답을 맞힐 확률을 예측하는 것

📌 기본 개념

문제 풀이 이력의 형태는 Xt = {qt, at}의 튜플 형태를 취합니다.

qt : 특정 문제의 태그 (개념, 예: 제곱근 문제, x-절편 문제 등)
at : 정오답 여부 (맞혔을 경우 1, 틀렸을 경우 0)

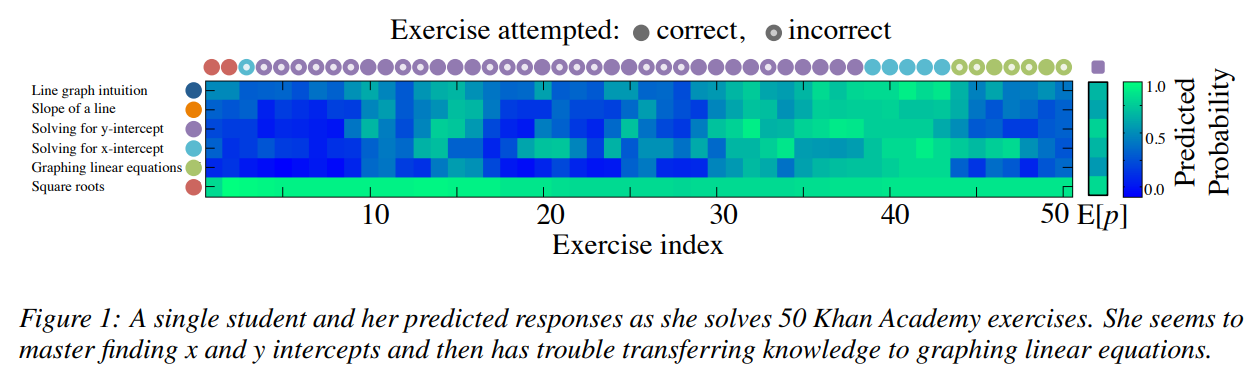
그림 1은 초등학교 8학년 수학을 배우는 학생 한 명의 추적 지식을 시각화한 것입니다. 학생은 먼저 두 개의 제곱근 문제에 올바르게 답한 다음 x절편 문제를 틀립니다. 학생은 문제를 풀 때마다 각 개념에 대한 다음 문제에서의 정오답 여부를 예측할 수 있습니다. 문제 풀이 이력 형태에는 각 문제의 태그(개념)이 필요한데요. 본 논문에서는 DKT의 경우, 전문가가 직접 다는 태그(개념)을 활용할 수 있지만, 그렇지 않더라도 모델이 스스로 학습하면서 문제의 내부 구조(내용적 하위 구조)를 자동으로 파악할 수 있다고 합니다.

2 Related Work

✅ 베이지안 지식 추적 (Bayesian Knowledge Tracing, BKT)

Bayesian Knowledge Tracing (BKT)는 학생의 학습 과정을 시간에 따라 모델링하는 가장 인기 있는 방법 중 하나입니다.

📌 기본 가정

1. 학생의 잠재적 지식 상태를 이진 변수로 표현, 각 변수는 특정 개념의 이해 여부를 나타냄
2. Hidden Markov Model(HMM) : 학생이 주어진 개념의 문제에 답할 때 각 이진 변수에 대한 확률을 업데이트하는 데 사용
3. 한 번 기술을 학습하면 결코 잊혀지지 않는다고 가정
4. 개별 학습자의 사전 지식, 추측해서 맞힐 확률, 실수할 확률, 문제 난이도 추정 포함
   [참고] BKT 매개변수 및 업데이트 방법

📌 한계점

1. 이진적 학생 이해 표현의 비현실성 : 학생의 이해도를 단순히 맞았다/틀렸다의 이진적 형태로 표현하는 것은 실제 학습 과정을 충분히 반영하지 못할 수 있습니다. 또한, 모델링 할 수 있는 활동의 종류에 제한을 가합니다.
2. 숨겨진 변수의 의미와 매핑의 모호성 : '숨겨진 변수들'은 학생이 각 문제를 얼마나 잘 이해하고 있는지를 나타내지만, 각 문제와 이 숨겨진 변수 사이의 매핑이 명확하지 않을 수 있습니다. 즉, 한 문제에 여러 개념이 포함되어 있을 수 있고, 학생이 문제를 풀 때 단순히 '하나의 개념'을 이해했다고 보기 어려운 경우가 많습니다. 이를 보완하기 위해 Cognitive Task Analysis(인지적 과제 분석) 등의 기술이 개발되었습니다.

✅ 기타 동적 확률 모델들

• Partially Observable Markov Decision Processes (POMDPs)
• Performance Factors Analysis (PFA), Learning Factors Analysis (LFA)
• Item Response Theory (IRT)

✅ 순환 신경망 (Recurrent Neural Networks, RNN)

순환 신경망은 시간에 따라 인공 뉴런을 연결하는 유연한 동적 모델입니다. 숨겨진 뉴런이 시스템에 대한 입력과 이전 활성화에 기반하여 진화한다는 점에서 정보 전파는 재귀적입니다. 교육 분야에서 동적 모델로 사용되는 숨겨진 마르코프 모델(Hidden Markov Models)과 달리, RNN은 잠재 상태를 고차원적이고 연속적인 형태로 표현합니다. RNN은 풍부한 표현력 덕분에 입력 정보를 나중에 예측할 때 사용할 수 있는 능력이 뛰어납니다. 특히 장단기 메모리(Long Short Term Memory, LSTM)에서 두드러집니다. LSTM은 RNN의 한 종류로, 장기 의존성을 모델링하는 데 강점을 가지고 있습니다.

3 Deep Knowledge Tracing

학습은 학습 자료, 학습 환경, 제시되는 순서, 학습자 개인의 특성 등 다양한 요소에 영향을 받기 때문에 단순한 이론만으로는 정확하게 측정하기 어렵습니다. 이를 해결하기 위해, 과거 학습 활동을 기반으로 학생의 문제 풀이 응답을 예측하는 데 두 가지 유형의 RNN(순환 신경망)을 적용하려고 합니다.

따라서 DKT는 과거 학습에 기반한 학생의 학습 응답을 예측하는 문제에 두 가지 RNN을 적용하였습니다.

• vanilla RNN(기본 RNN 모델, 시그모이드 유닛 사용)
• LSTM(장단기 메모리) 모델

✅ 모델

📌 전통 RNNs

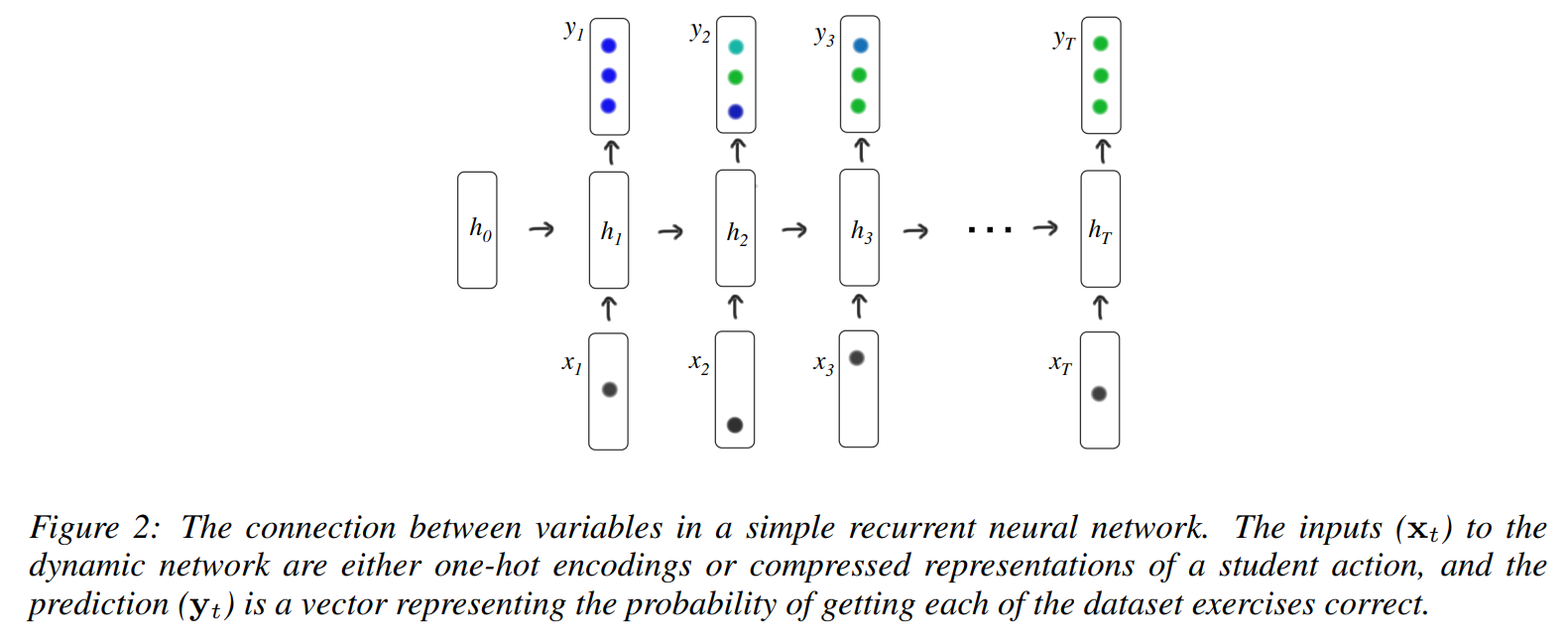
• 입력 벡터 시퀀스 X1,...,X𝑇(one-hot 인코딩 또는 학생의 행동을 압축된 표현으로 나타낸 것)를 출력 벡터 시퀀스 Y1,...,Y𝑇(각 데이터셋의 문제를 맞힐 확률을 나타내는 벡터)로 매핑

• '숨겨진' 상태 ℎ1,...,ℎ𝑇가 계산 : 과거 관찰치로부터 얻은 정보를 인코딩하여 미래 예측에 사용됨

• 상태 ℎ𝑡 업데이트
  

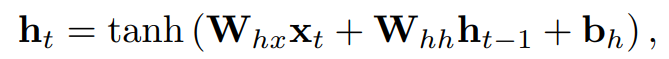
• 출력 Y𝑡는 시그모이드 함수로 계산
  

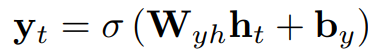
• 파라미터

  입력 가중치 행렬 𝑊ℎ𝑥
  순환 가중치 행렬 𝑊ℎℎ
  초기 상태 ℎ0
  출력 가중치 행렬 𝑊𝑦ℎ

• 편향

  숨겨진 상태의 편향 𝑏ℎ
  출력 유닛의 편향 𝑏𝑦

📌 LSTM

• RNNs의 복잡한 변형으로, 보통 더 강력한 성능을 발휘
• forget gate(망각 게이트)를 사용해 명시적으로 정보를 지우기 전까지 정보를 더 오랫동안 유지함으로써 훈련하기 쉬움
• LSTM의 숨겨진 유닛은 증가하는 상호작용을 사용해 업데이트되며, 같은 수의 잠재 유닛으로 더 복잡한 변환 수행 가능
• LSTM의 업데이트 수식
  

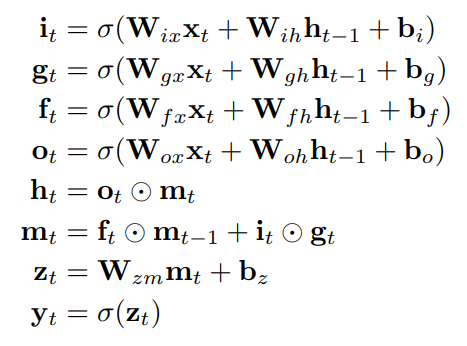
✅ Input & Output Time Series

RNN이나 LSTM을 학생의 문제 풀이에 대해 훈련시키기 위해서는 문제 풀이 이력을 고정 길이의 입력 벡터
X𝑡의 시퀀스로 변환해야 합니다. 풀이 이력의 특성에 따라 두 가지 방법으로 수행됩니다.

📌 고유한 개념의 수가 적은 경우 Input

• 학생 풀이이력인 튜플 형태의 ℎ𝑡={𝑞𝑡,𝑎𝑡}에 원-핫 인코딩을 사용하여 입력 벡터 𝑥𝑡 설정
• 벡터 X𝑡는 각 문제에 대해 맞혔는지 틀렸는지를 포함한 정보를 담고 있으므로 0과 1로만 이루어진 2𝑀 차원의 벡터
  

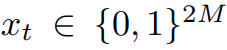
📌 고유한 개념의 수가 많은 경우 Input

데이터셋에 feature가 많은 경우 원-핫 인코딩을 하면 각 문제마다 고유한 위치에 1을 기록해야 하기 때문에, 인코딩된 벡터가 매우 커져서 비효율적이 됩니다. 따라서 고유한 개념의 수가 많은 경우 원-핫 인코딩 대신 압축 센싱에서 영감 받은 방법으로 랜덤 벡터를 할당합니다.

• 압축 센싱(Compressed Sensing)에서 영감 받은 원-핫 고차원 벡터의 랜덤 저차원 표현
  압축 센싱 이론에 따르면, k-sparse 신호(즉, 대부분의 값이 0이고 일부 값만 1인 신호)는 고차원 공간에서 k log d 개의 랜덤 선형 투영으로 정확하게 복원될 수 있습니다. 여기서 𝑑는 신호가 있는 공간의 차원입니다.
  One-hot 인코딩은 1-sparse 신호(오직 하나의 값만 1이고 나머지는 0인 신호)이므로, 이를 낮은 차원의 랜덤 가우시안 벡터로 표현할 수 있습니다. 이 벡터의 길이는 대략 𝑙𝑜𝑔2𝑀 정도로 설정됩니다.

  쉽게 정리하면, 압축 센싱은 중요한 데이터를 일부 선택하여 저장한 뒤, 나중에 이 중요한 정보들을 기반으로 전체 데이터를 다시 복원합니다. 따라서 전체 데이터를 다 저장하지 않아도 되기 때문에 데이터를 효율적으로 처리할 수 있습니다.

• 풀이 이력 튜플 {𝑞𝑡, 𝑎𝑡}에 대해 **정규분포 𝑁(0,𝐼)에서 랜덤 벡터 n𝑞,𝑎를 샘플링 (이 벡터는 𝑁-차원 벡터로, 𝑁은 문제의 수 𝑀보다 훨씬 작은 값)
• 각 입력 벡터 X𝑡는 해당 상호작용 튜플 {𝑞𝑡, 𝑎𝑡}에 대응되는 랜덤 벡터 n𝑞𝑡,𝑎𝑡로 설정

📌 Output

출력 벡터 Y𝑡는 문제의 수와 동일한 길이를 가지며, 각 항목은 학생이 특정 문제를 올바르게 풀 확률을 나타냅니다. 따라서 a𝑡+1의 예측은 Y𝑡에서 q𝑡+1에 해당하는 항목으로부터 읽을 수 있습니다.

✅ 최적화

모델의 학습 목표는 학생 응답 시퀀스의 음의 로그 가능도(Negative Log Likelihood)를 최소화하는 것입니다. 즉, 모델이 예측한 학생의 답변과 실제 답변 간의 차이를 줄이는 것을 목표로 합니다.

📌 원-핫 인코딩

𝛿(𝑞𝑡+1)는 학생이 시간 𝑡+1에 푼 문제에 대한 one-hot 인코딩을 나타냅니다. 이 벡터는 학생이 푼 문제를 나타내며, 해당 문제의 위치에 1이, 나머지에는 0이 들어갑니다.

📌손실 함수(Loss function):

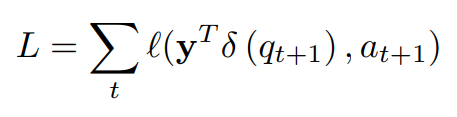
• Binary Cross Entropy (이진 교차 엔트로피)를 손실 함수로 사용
• 모델의 예측값 Y𝑇와 실제 학생 응답 𝛿(q𝑡+1),a𝑡+1 사이의 차이를 측정
• 예측된 Y𝑇와 실제 정답 간의 차이가 클수록 손실 값이 커지고, 작을수록 손실 값이 줄어듬
• 손실 함수 𝐿는 학생의 모든 시간 단계에 대해 계산되며, 각각의 𝑡에 대해 예측값 Y𝑇와 실제 응답
  𝛿(q𝑡+1),a𝑡+1 사이의 오차를 더한 값

📌 최적화 방법

• 손실을 최소화하기 위해 미니배치 확률적 경사 하강법(Stochastic Gradient Descent, SGD)를 사용
• 드롭아웃 적용 : 모델이 훈련 데이터에 너무 과적합(overfitting)되지 않도록 특정 층에서 일부 뉴런을 무작위로 제외하여 훈련, h𝑡를 사용하여 Y𝑡를 계산할 때 적용되지만, 다음 숨겨진 상태 ℎ𝑡+1을 계산할 때는 적용되지 않음
• Gradient truncating : RNN이나 LSTM과 같은 순환 신경망에서는 시간에 따라 역전파할 때 기울기가 폭발하는 문제를 방지하기 위해, 기울기가 특정 임계값을 넘으면 기울기를 자름
• 숨겨진 상태(hidden state)의 차원 : 200
• 미니배치 크기 : 100

4 Educational Applications

✅ 교육 과정 개선

DKT 모델은 학생에게 가장 적합한 학습 항목을 순서대로 추천하는 데 큰 영향을 미칠 수 있습니다.예를 들어, 학생이 50개의 문제를 푼 후, 모델은 그 학생의 현재 지식 상태를 기반으로 다음에 풀어야 할 문제를 예측할 수 있습니다. 모델은 특정 문제를 풀게 했을 때 학생의 기대되는 지식 상태를 계산하고, 가장 최적의 문제를 추천할 수 있습니다.

✅ 문제 간 관계 발견

DKT 모델은 문제들 간의 숨겨진 관계를 발견하는 데에도 활용될 수 있습니다. 이는 일반적으로 교육 전문가들이 수행하는 작업입니다. 문제 𝑖를 맞힌 후 문제 𝑗에 대한 모델의 정답 확률을 계산한 다음, 다른 모든 문제와의 비교를 통해 문제들 간의 의존성을 계산합니다. 이 계산을 통해 문제 간 선행 학습 관계를 발견할 수 있으며, 모델이 학습한 데이터로부터 필수 학습 항목들을 자동으로 파악할 수 있습니다.

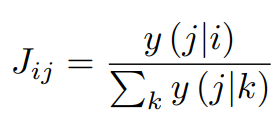
5 Datasets

DKT 모델을 평가하기 위해 사용한 3가지 데이터셋에 대한 설명입니다. 각 데이터셋에서 학생의 성과를 예측하는 모델의 능력을 평가하기 위해 AUC(Area Under the Curve)를 사용하며, 5-fold 교차 검증을 통해 결과를 평가했습니다.

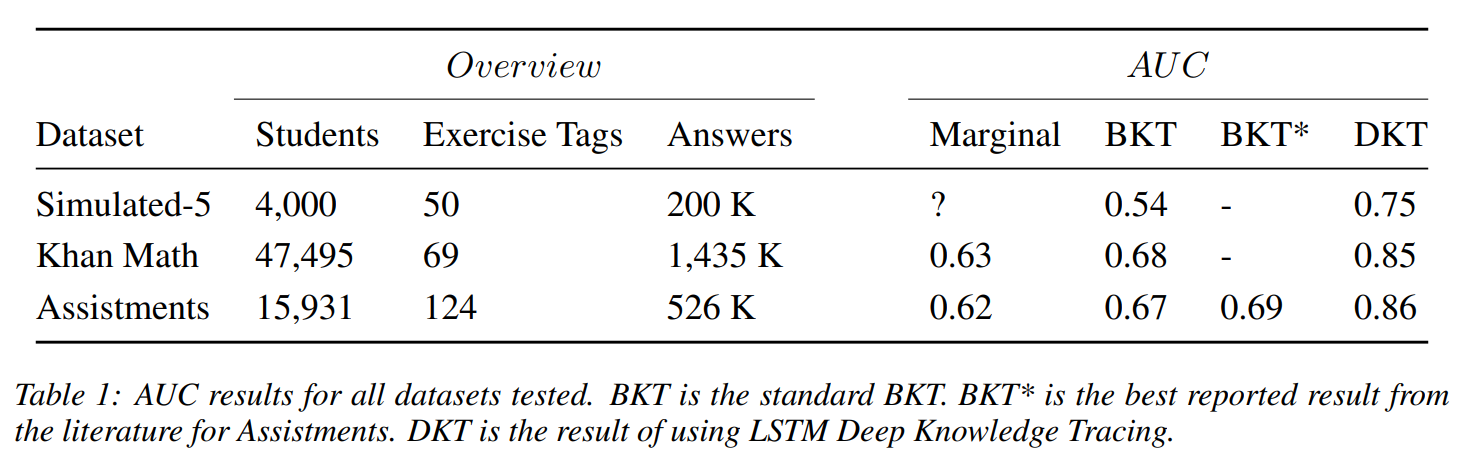
1. 시뮬레이션 데이터
가상 학생과 개념을 학습하는 가상 환경을 설정하여 모델을 테스트합니다. 2,000명의 가상 학생이 50개의 문제를 풀고, 문제는 5개의 개념 중 하나에 속합니다. 각 학생은 각 개념에 대해 잠재적인 기술 수준(α)을 가지고 있으며, 문제는 난이도(β)를 가지고 있습니다. 아이템 반응 이론(Item Response Theory)을 기반으로, 학생이 문제를 맞출 확률을 계산합니다. 여기서 𝑐는 랜덤 추측의 확률입니다. 각 실험은 20번 반복되며, 각 실험마다 다른 랜덤 데이터를 사용하여 평균 정확도와 표준 오차를 계산합니다.

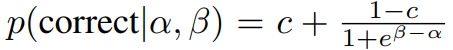
2. Khan Academy 데이터
8학년 공통 교육 과정에 대한 Khan Academy의 익명 학생 활동 데이터를 사용했습니다. 47,495명의 학생이 1.4백만 개의 문제를 완료했으며, 69개의 다른 문제 유형을 다룹니다.

3. Assistments 벤치마크 데이터셋
Assistments 2009-2010 "skill builder" 공개 벤치마크 데이터셋을 사용해 DKT 모델을 평가했습니다. Assistments는 초등학교 수학을 가르치고 평가하는 온라인 튜터로, 현재까지 공개된 지식 추적 데이터셋 중 가장 큰 규모입니다.

6 Results

DKT 모델은 기존의 BKT 모델보다 뛰어난 예측 성능을 보였으며, 특히 잠재 개념 간의 관계를 잘 학습하여 학생 성과 예측 및 커리큘럼 최적화에 유용한 도구로 활용될 수 있음을 증명했다고 합니다.

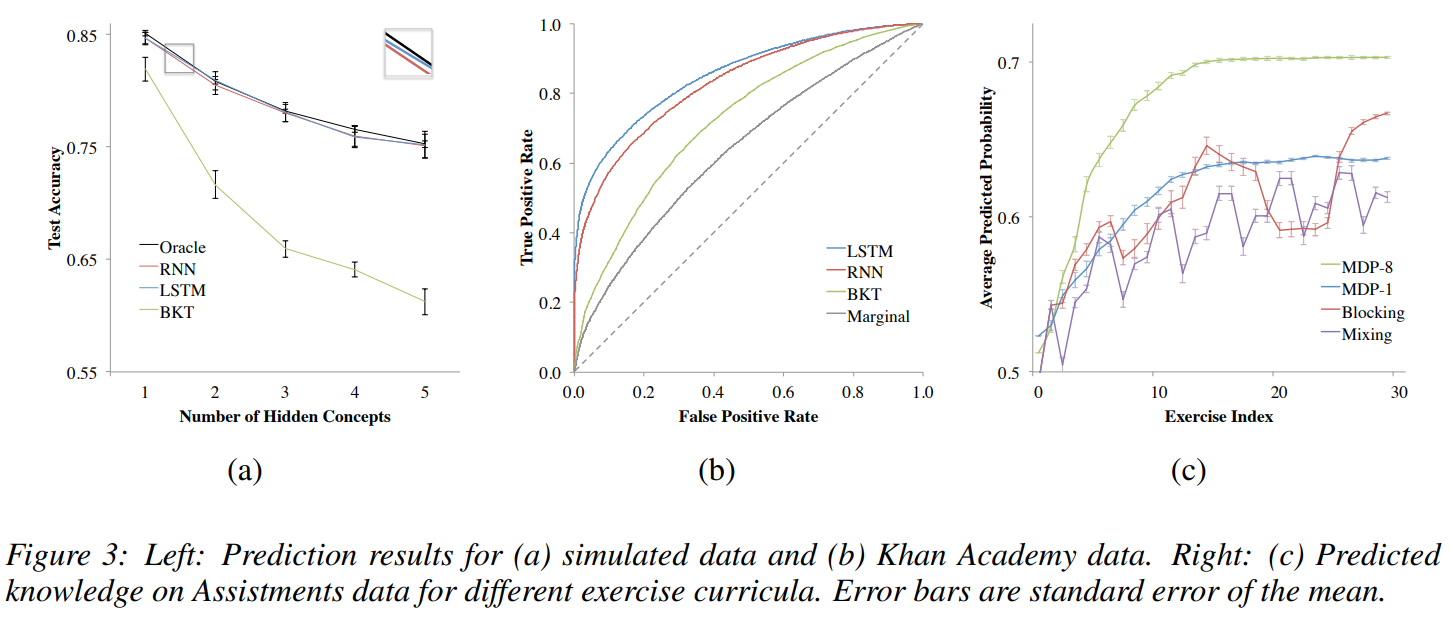
7 Discussion

Assistments 벤치마크와 Khan Academy 데이터셋에서 이전 최고 성능보다 우수한 결과를 보였습니다.
특히 두 가지 중요한 특성이 강조되었습니다.

1. 전문가의 개입 없이 스스로 학습 패턴을 파악할 수 있다는 점.
2. 벡터화할 수 있는 모든 학생 입력 데이터에서 작동할 수 있다는 점.

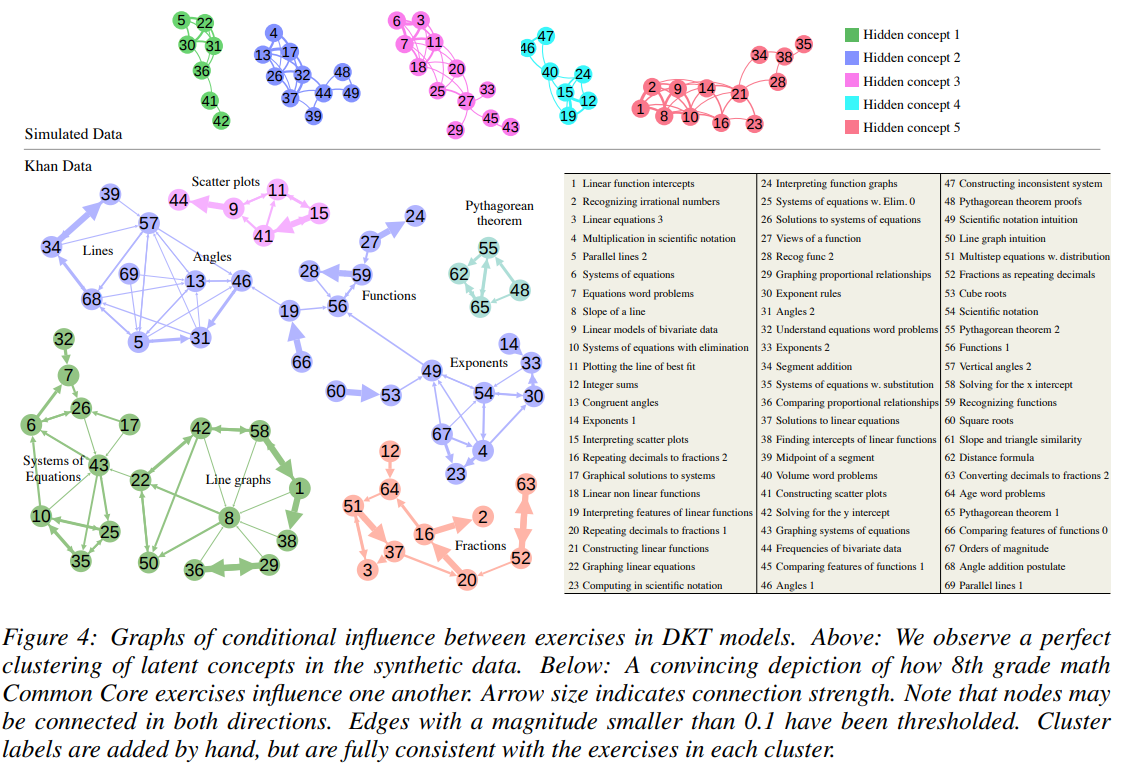
하지만 RNN은 대규모 데이터가 필요하므로 온라인 교육 환경에 적합하지만, 소규모 교실 환경에서는 효과가 제한적일 수 있습니다. 아래 그래프는 DKT 모델을 통해 잠재 개념들이 잘 연결된 모습(상단)과 문제들 간 연결 방향 및 강도가 표시된 그래프(하단)을 보여줍니다.

---

DKT 이후 여러 발전된 모델들이 많이 나왔지만 DKT는 여전히 많이 활용되고 있는 지식 추적 모델입니다. 지식 추적을 스터디하면서 이번 포스팅에서는 10년이 되어가는 DKT 논문을 제대로 다시 읽어보았습니다. DKT를 적용하여 학생의 지식을 정확하게 추적하고 적절한 학습 콘텐츠를 추적하는 서비스를 개발할 방안을 계속해서 알아볼 예정입니다. 나아가 GKT를 포함한 발전된 KT 모델들과 상황별 적합한 KT 모델들을 살펴보고자 합니다.