✅ 지식공간이론 (KST)
지식공간이론(이하 KST)은 Doignon과 Falmagne(1985)의 논문에서 시작된 이론으로, 학습자의 지식의 흐름과 상태를 설명하기 위해 특정한 공간을 구조적인 형태로 표현하여 분석하는 방법입니다. 평가를 통해 개인의 '지식 상태', 즉 개인이 마스터한 정확한 개념 집합을 밝혀내야 한다는 것을 목적으로 합니다. SAT, ACT와 같은 평가 절차와는 바로 Adaptive(적응형 평가, 학생 이전 답변의 가능한 정확성 고려) 하다는 점에서 근본적인 차이가 있습니다. 따라서 학생들의 학습 평가 결과를 지식 공간에 반영하고 각 단계별 지식 체계를 분석하여 결과적으로 학생들의 학습 효과를 최대화 하는데 이용되어 왔습니다. 이번 포스팅에서는 Doignon과 Falmagne(2015)의 Knowledge Spaces and Learning Spaces 논문에 정리되어 있는 KST 관련 개념들을 살펴보겠습니다.
✅ Item & Instance
KST에서 개념(concept)이란 '개인이 습득하는 데 배운 문제 유형'입니다. 이때 문제 유형은 Item이라고 하는데, 심리 측정에서는 특정 문제를 Item이라고 하지만 KST에서는 문제를 Instance라고 합니다. 예시는 다음과 같습니다.
Item : 2차 다항식의 근 계산
Instance : 방정식 x² +5x + 6 = 0의 근을 구하시오.
✅ Knowledge Structure
지식 구조는 (𝑄,𝐾) 쌍으로 정의됩니다. 여기서 𝑄는 도메인이라 불리는 특정한 지식 영역을 나타내는 집합입니다. 도메인은 최대 650개의 항목을 포함하는 지식 상태인데, 지식 상태는 하위 요소의 특정 모음인 지식 공간 또는 학습 공간을 형성합니다. 학습 공간은 수백만 개의 상태를 포함할 수 있습니다.
𝐾는 𝑄의 부분집합들로 이루어진 모음(collection)입니다. 이 부분집합들은 학습자가 지식을 어느 정도 알고 있는지를 나타냅니다. 중요한 조건은 빈 집합 ∅(아무런 개념도 모르는 상태)과 도메인 𝑄 자체(모든 지식을 알고 있는 상태)도 𝐾에 포함되어 있어야 합니다. 예시는 다음과 같습니다.
즉, 지식 구조는 학습자가 𝑄에 속한 개념들을 알고 있는 다양한 상태들을 나타내는 구조입니다.
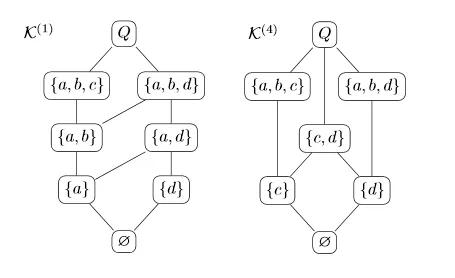
Q = {a,b,c,d}
K = {∅, {a}, {d}, {a,b}, {a,d}, {a,b,c}, {a,b,d}, Q}
*Q의 각 하위 집합은 지식 상태입니다. 예를 들어, 상태 {a,b,d}는 항목 a, b, d의 지식을 의미합니다.
📌 Finite Knowledge Structure (유한 지식 구조)
유한 지식 구조는 도메인 𝑄가 유한한 개념들로 구성된 경우를 의미합니다. 즉, 학습자가 습득할 수 있는 개념의 수가 제한된 경우를 말합니다.
📌 Discriminative Knowledge Structure (식별 가능한 지식 구조)
지식 구조가 discriminative하다는 것은, 도메인의 각 개념이 다른 개념들과 구분 가능하다는 뜻입니다. 구체적으로, 어떤 두 개념 𝑞와 𝑟에 대해, 그 개념들을 포함하고 있는 지식 상태 집합 𝐾𝑞와 𝐾𝑟이 같다면, 𝑞와 𝑟는 같은 개념이어야 한다는 조건입니다. 예를 들어, 𝑞라는 개념을 포함하는 모든 지식 상태가 𝑟을 포함하는 지식 상태와 동일하다면, 𝑞와 𝑟는 같은 개념이어야 합니다. 즉, 각 개념은 고유한 학습 상태를 통해 식별할 수 있어야 한다는 것입니다.
✅ Knowledge Space
지식 공간은 합집합에 따라 닫힌 지식 구조입니다. 합집합에 따라 닫힌 것은 K에 속하는 두 상태의 합집합에서 가능한 모든 결과는 반드시 K에 속해야 함을 의미합니다. 이 속성은 작은 요소 집합의 조합으로 전체 지식 구조를 정의할 수 있게 해줍니다.
✅ Learning Space
학습 공간은 특정한 규칙을 따르는 지식 구조입니다. 여기서 지식 구조란 학습자가 어떤 상태에서 알고 있는 개념들의 집합이고, 학습 공간은 이러한 지식 상태들이 학습 과정에서 일관적이고 순차적으로 확장되는 구조입니다.
학습 공간은 두 가지 조건을 포함해야 합니다.
📌 [L1] Learning Smoothness(학습의 매끄러움)
이 조건은 학습자가 새로운 개념을 배울 때, 이미 그 개념을 학습할 준비가 되어 있어야 한다는 뜻입니다. 즉, 새로운 개념을 배우기 전에 필요한 기초 지식을 이미 알고 있어야 한다는 것입니다. 예를 들어, 더 복잡한 수학 개념을 배우기 전에 기본 개념을 먼저 배워야 한다는 식으로, 학습이 순차적으로 이루어지도록 합니다. 이 조건은 학습자가 새로운 개념을 배울 때, 하나씩 차례로 배워야 한다는 규칙을 의미합니다.
📌 [L2] Learning Consistency(학습의 일관성)
이 조건은 학습자의 지식이 일관성을 유지해야 한다는 의미입니다. 학습자가 새로운 지식을 추가로 배울 때, 그 새로운 지식이 이미 알고 있는 다른 지식들과 모순되지 않아야 한다는 것입니다.
📌 예시
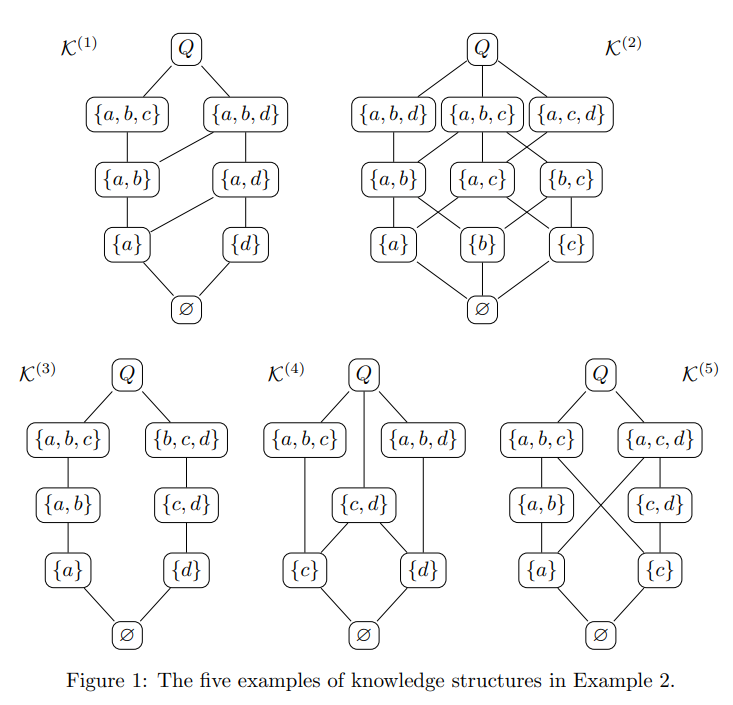
𝐾(1)부터 𝐾(5)까지가 있는데, 이 중에서 𝐾(1)과 𝐾(2)만이 학습 공간의 두 조건을 모두 만족합니다. 𝐾(3)는 첫 번째 조건인 [L1]은 만족하지만, 두 번째 조건 [L2]는 만족하지 않습니다. 예를 들어, 학습 상태가 ∅에서 {𝑎}로 확장되는 상황에서 {𝑑}를 추가하려면 문제가 생깁니다. 𝐾(4)는 [L2]는 만족하지만, [L1]을 만족하지 않습니다. {c}와 {𝑑}에서 각각 {a,b,c}와 {a,b,d}로 갈 때 {a}와 {b}를 마스터 했어야 하기 때문입니다. 𝐾(5)는 두 조건 모두를 만족하지 않습니다.
✅ Atom
KST에서 원자는 특정 항목 q를 포함하는 지식 공간 K의 최소 상태입니다. 즉, q를 포함하고 있지만 더 작은 상태로 나눌 수 없는 상태입니다. 교육적 관점에서 q를 마스터하기 전에 q의 원자 내 항목 집합을 마스터해야 하기 때문에 중요합니다.
Item A : 한 자리 수 덧셈
Item B : 두 자리 수 덧셈
Item C : 세 자리 수 덧셈
항목 C를 마스터하기 전 항목 B를 마스터해야 하고, 항목 B를 마스터하기 전 항목 A를 마스터해야 합니다. 이를 KST로 표현하면 A를 포함하는 최소 상태, 즉 원자는 {A}입니다. B의 원자는 B 마스터 전 A를 마스터해야 하므로 {A,B}, C의 원자는 {A,B,C}가 됩니다.
✅ Fringe Theorem
프린지 정리는 학습 공간에서 학생의 지식 상태를 Inner Fringe와 Outer Fringe로 구분합니다. 학습 공간에서는 어느 상태이든 해당 상태의 Inner Fringe와 Outer Fringe로 구성된 쌍으로 명시됩니다.
📌 Inner Fringe
주어진 상태 K에서 내부 프린지는 K에 포함되어 있으면서 해당 상태에서 제거했을 때 여전히 존재하는 항목의 집합입니다. 공집합은 항상 비어 있는 내부 프린지를 가집니다.
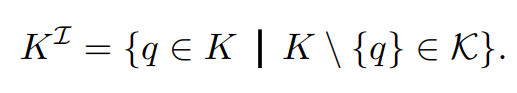
📌 Outer Fringe
주어진 상태 K에 포함되지 않지만 K에 포함시킬 경우 상태가 존재하게 되는 항목의 집합입니다. 전체 도메인 Q는 비어 있는 외부 프린지를 가집니다. 외부 프린지는 학생이 학습할 준비가 되어 있는 내용을 알려주기 때문에 교육적 관점에서 중요합니다. ALEKS의 수십만 개 평가 데이터를 기반으로 한 연구에 따르면 외부 프린지에 포함된 항목을 성공적으로 학습할 확률은 약 93%로 추정됩니다.
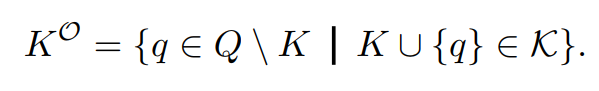
원문
참고자료
이상훈 ( Sanghoon Lee ), 문승진 ( Seung-jin Moon ). "결정적 학습 경로를 위한 지식 구조 분석 시스템." 인터넷정보학회논문지 16.6 (2015): 39-46.
Introduction to Knowledge Space TheoryㅣMedium
