[Algorithm]Divide and Conquer

Divide and Conquer이란?

복잡한 문제를 작고 단순한 문제로 나눈 후, 각각을 해결하고 다시 합쳐서 전체 문제를 푸는 알고리즘 설계 기법

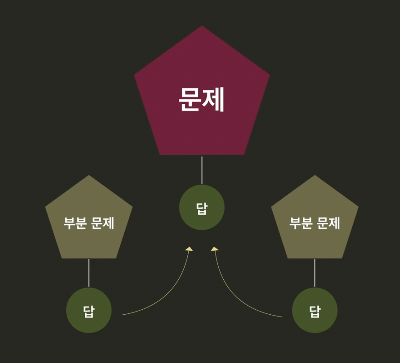
해결과정

1. Divide (분할)

문제를 더 작은 부분 문제(subproblem)로 나눈다.

2. Conquer (정복)

분할된 작은 문제를 재귀적으로 해결한다.

충분히 작아지면 직접 해결한다 (기저 조건: base case).

3. Combine (결합)

해결된 작은 문제의 해답을 결합하여 원래 문제를 해결한다.

장단점

장점

• 큰 문제를 재귀적으로 나누어 해결하기에 간단하지만 빠르며 병렬적으로 문제를 해결할 수 있다는 장점이 있다.

단점

• 재귀적으로 문제를 해결하기 때문에 인풋이 너무 큰 경우 많은 프로그래밍 언어에서 Stack Overflow가 발생할 수 있으며, 이는 메모리의 비효율적 사용을 뜻한다.

예제_병합정렬

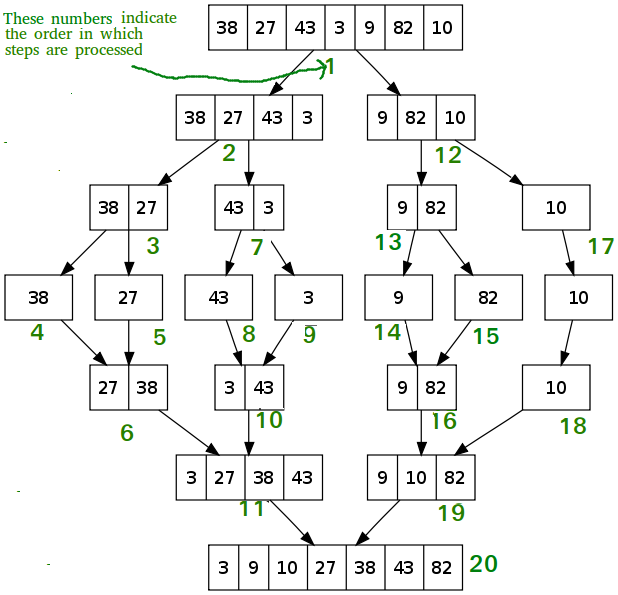
예제 코드

public class MergeSort {

    // 병합 정렬을 수행하는 메서드
    public static void mergeSort(int[] arr, int left, int right) {
        // 배열의 왼쪽 인덱스가 오른쪽 인덱스보다 작을 때만 수행
        if (left < right) {
            // 중간 지점 계산
            int mid = (left + right) / 2;

            // 왼쪽 절반 정렬
            mergeSort(arr, left, mid);

            // 오른쪽 절반 정렬
            mergeSort(arr, mid + 1, right);

            // 정렬된 두 부분 병합
            merge(arr, left, mid, right);
        }
    }

    // 정렬된 두 배열을 병합하는 메서드
    public static void merge(int[] arr, int left, int mid, int right) {
        // 왼쪽과 오른쪽 부분 배열의 크기 계산
        int n1 = mid - left + 1;
        int n2 = right - mid;

        // 왼쪽과 오른쪽 부분 배열 생성
        int[] L = new int[n1];
        int[] R = new int[n2];

        // 원본 배열에서 왼쪽 절반을 L[]에 복사
        for (int i = 0; i < n1; ++i)
            L[i] = arr[left + i];

        // 원본 배열에서 오른쪽 절반을 R[]에 복사
        for (int j = 0; j < n2; ++j)
            R[j] = arr[mid + 1 + j];

        // 병합 과정 시작
        int i = 0, j = 0;     // L[], R[]의 인덱스
        int k = left;         // 원본 배열(arr)의 시작 인덱스

        // 두 배열을 비교하면서 더 작은 값을 원본 배열에 복사
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k++] = L[i++];  // L의 값이 작거나 같으면 복사
            } else {
                arr[k++] = R[j++];  // R의 값이 작으면 복사
            }
        }

        // L[]에 남은 요소가 있으면 모두 복사
        while (i < n1) {
            arr[k++] = L[i++];
        }

        // R[]에 남은 요소가 있으면 모두 복사
        while (j < n2) {
            arr[k++] = R[j++];
        }
    }

    // 배열의 내용을 출력하는 메서드
    public static void printArray(int[] arr) {
        for (int value : arr)
            System.out.print(value + " ");
        System.out.println();
    }

    // 메인 함수: 프로그램 실행 시작점
    public static void main(String[] args) {
        // 테스트할 배열 선언
        int[] arr = { 38, 27, 43, 3, 9, 82, 10 };

        System.out.println("정렬 전 배열:");
        printArray(arr);  // 정렬 전 배열 출력

        // 병합 정렬 실행
        mergeSort(arr, 0, arr.length - 1);

        System.out.println("정렬 후 배열:");
        printArray(arr);  // 정렬 후 배열 출력
    }
}