
Dynamic Programming이란?
(=복잡한 문제를 작은 하위 문제로 나누어 푸는 방식)
큰 문제를 작은문제로 나누어 푸는 문제를 일컫는 말
Divide and Conquer(분할정복)과 비교
| 항목 | Divide and Conquer (분할정복) | Dynamic Programming (동적 프로그래밍) |
|---|---|---|
| 문제 분할 | 문제를 작은 독립적인 부분 문제로 분할 | 문제를 작은 중복되는 부분 문제로 분할 |
| 중복 문제 | 중복 없음 → 같은 하위 문제를 여러 번 계산 X | 중복 있음 → 같은 하위 문제 반복 계산 O |
| 적용 예시 | 병합 정렬(Merge Sort), 퀵 정렬(Quick Sort), 이진 탐색 | 피보나치, LCS, 배낭 문제, 계단 오르기 |
| 대표 접근 방식 | 재귀 | 재귀 (Top-Down) 또는 반복문 (Bottom-Up) |
동적 프로그래밍 적용 조건
1. 중복되는 부분 문제 (Overlapping Subproblems)
전체 문제를 해결하는 과정에서 같은 하위 문제가 반복해서 등장한다.
예를 들어, 피보나치 수열에서 fib(n-1)과 fib(n-2)를 구할 때, fib(n-3)은 두 번 호출됨.
👉 반복 계산을 줄이기 위해 메모이제이션(Memoization)이나 테이블(Tabulation)을 사용해 저장하고 재사용함.
2. 최적 부분 구조 (Optimal Substructure)
전체 문제의 최적 해가 하위 문제의 최적 해를 통해 구성될 수 있어야 한다.
즉, 부분 문제들의 해를 조합해 전체 문제의 해를 만들 수 있어야 함.
예를 들어, 최단 경로 문제에서 어떤 지점까지의 최단 거리도 이전에 계산한 경로를 기반으로 구할 수 있음.
동적 프로그래밍 구현 방식
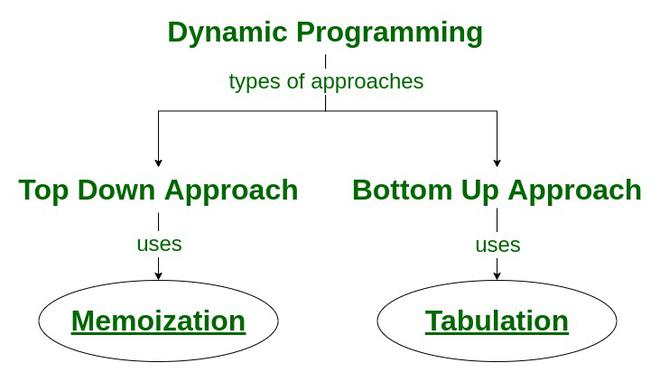
1. Top-Down 방식 (Memoization)
재귀 함수 + 메모이제이션을 이용한 방식
큰 문제를 해결하기 위해 작은 문제를 재귀적으로 호출하면서, 이미 계산한 결과는 저장해 중복 계산을 피함.
- 특징
자연스럽게 문제를 분할하면서 접근 가능 → 코드가 직관적
메모이제이션을 위한 저장소(dict 또는 배열)가 필요함
2. Bottom-Up 방식 (Tabulation)
작은 문제부터 차례대로 해결하며 테이블을 채워가는 방식
반복문을 사용하여 작은 문제부터 점차적으로 큰 문제로 확장해 나감.
- 특징
배열이나 리스트를 이용한 반복문 기반 구현
전체 테이블을 채우기 때문에, 모든 경우를 고려함
* Memorization
재귀 호출을 사용하는 알고리즘에서,
이미 계산한 결과를 메모리(보통 딕셔너리나 배열)에 저장해두고
같은 입력이 들어오면 저장된 결과를 바로 반환하는 기법.