이번에 새롭게 공부하기 시작한 diffusion model 논문이다.
우선 이 논문은 DDPM논문을 읽었다는 전제하에 시작한다.
안읽어보신 분은 읽어보시길 -> DDPM 논문

Diffusion model의 시초라고 볼 수 있는 논문이기 때문에 Diffusion 연구하시는 분들은 필수코스!~

그럼 DDRM 논문 리뷰 스타트~

Abstract

우선 DDRM은 이름에서 볼 수 있듯이 Restoration에 특화된 모델이다.
해당 논문에서는 Blurring, JPEG과 같이 Degraded 이미지들을 복원하는 용도의 논문이라고 설명하고 있고 특히 아래와 같이 정의하였다.

This work addresses these issues by introducing Denoising Diffusion Restoration Models (DDRM), an efficient, unsupervised posterior sampling method.

DDRM을 비지도적인 사후 샘플링 방법이라고 하는데, 여기서 말하는 비지도 학습은 특정 Inverse task(EX. Super resolution, ...) 별로 네트워크를 훈련하는 것이 아닌, 원본 이미지 x만으로 학습한다는 것을 의미한다.

따라서 DDRM은 Inverse Problem에 대한 지도학습은 하지 않고, 이미지 자체만으로 학습된 diffusion model을 inverse문제에 응용한다.

Introduction

기존의 이미지 복원(Super resolution/Deblurring/Inpainting/Colorization/Compressive Sensing)은 선형 역문제로 정의되어 왔다.
즉 noise가 낀 관측값을 통해 원본 이미지를 복원하는 문제를 말한다.

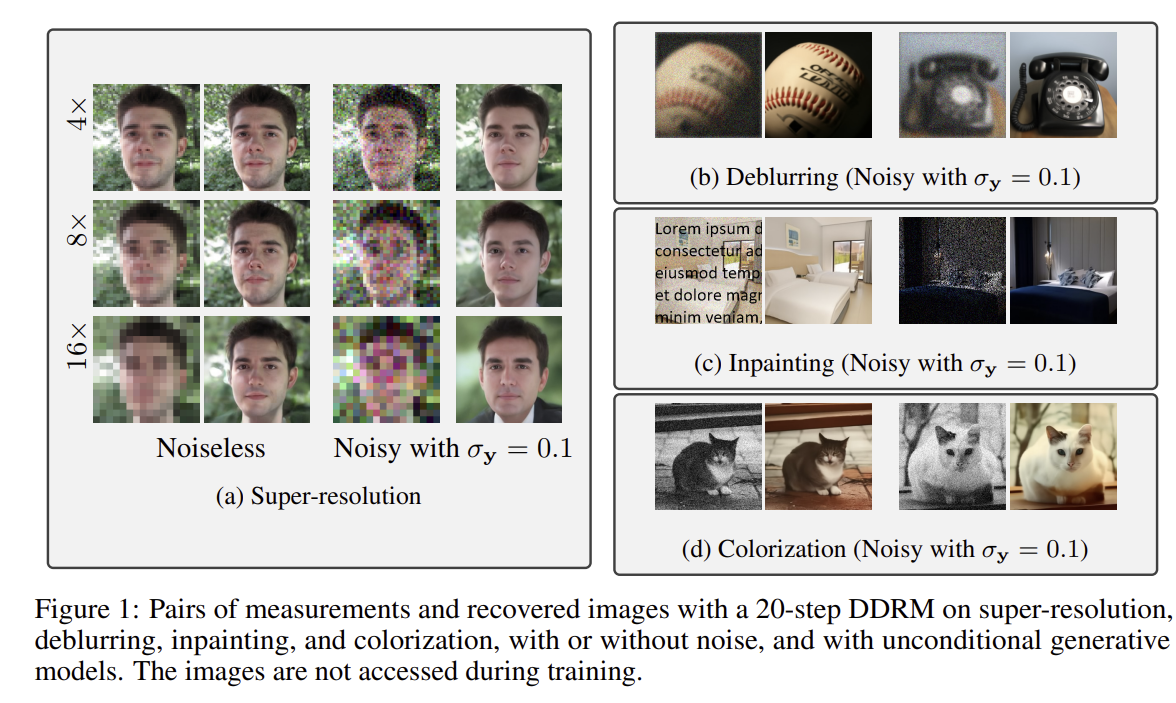
이러한 선형 역문제에 대해 여러 접근방식이 제안되어 왔는데, 해당 논문에서는 크게 2개로 나누어 정리한다.

1. 기존 접근법: Supervised Learning
   • 원본/Degradation 이미지에 대해 end-to-end supervised 학습
   • But, 의료 영상처럼 수많은 degradation model에 대응해야 하는 경우, 매번 다시 학습하는 supervised 방법은 비효율적
2. 대안: Unsupervised + Learned Priors
   • 학습 시 degradation model없이 , inference 시에만 degradation model을 사용하는 unsupervised 접근
   • 이미지 구종 대한 좋은 prior를 학습
   • 한계 (계산 복잡 + Hyperparameter에 민감)
     • Optimization(MAP)이나 Sampling으로 복원
     • 보통 iterative 방법(Gradient Descent, Lange
     • Prior(복원하기 전에 이미 알고 있는 정보나 가정) + Likelihood(현재 우리가 가진 측정값 또는 관측된 데이터) => Posterior(원래 어떤 이미지였을까?) 계산

이러한 한계를 개선하고자 한 모델이 DDRM이다.

DDRM is a denoising diffusion generative model that gradually and stochastically denoises a sample to the desired output, conditioned on the measurements and the inverse problem.

DDRM은 다음과 같이 측정값(손상된 입력 이미지)와 Inverse problem(원본 이미지를 추정하는 문제)를 조건으로 하여 샘플을 점진적, 확률적으로 denoising하여 원하는 출력으로 복원하는 diffusion model이다.

이 과정을 통해 DDRM은 Posterior분포를 학습하는 variational inference 목적 함수를 도입한다.

Variational Inference(변분추론): Posterior분포를 근사하는 방법. 즉, 원본 이미지가 얼마나 그럴듯한지, 무엇일지에 대한 확률적인 분포

Background

Linear Inverse Problem

일반적으로 선형 역문제는 아래와 같이 정의한다.

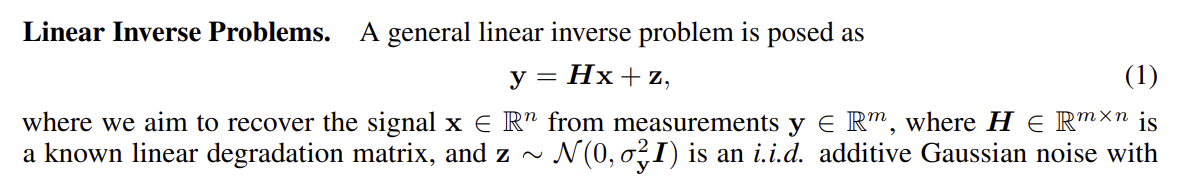
y: noise가 섞이거나 손상된 이미지
H: 원본 이미지 x를 망가뜨리는 연산 (ex. blur filer, downsampling)
x: 복원하려는 원본 이미지
z: 평균 0, 분산 σ²를 갖는 gaussian noise

즉 y는 x에 H로 손상시키고, 노이즈 z를 더한 것이다.
우리는 이제 y를 보고 x를 복원할 예정!

이를 복원하는 방법을 해당 파트에서는 2개로 나누어 설명하는데,
1) Bayesian Sampling 기반 방법
2) Supervised Learning 기반 방법
이다.

이는 각각 아래와 같다고 함. (Feat. GPT)

Denoising Diffusion Probabilistic Models

글의 처음에 언급했던 DDPM은 샘플 데이터를 통해 데이터 분포 q(x)를 근사하는 모델 분포 pθ(x)를 학습한다.

Diffusion model은 xt∈ Rⁿ일 때, 아래와 같은 Markov chain을 따른다.

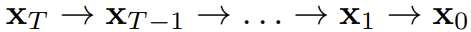
pθ(x0:T)는 아래와 같이 T부터 0까지 각 단계에서 조건부 확률을 곱한 결합 분포로 표현된다.
즉 매 단계마다 조건부 분포로 노이즈를 제거하면서 x_T에서 x_0으로 향해가는 것!

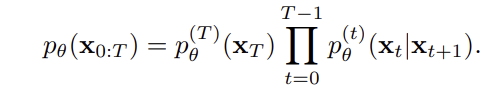
아래는 학습에 필요한 노이즈를 추가하는 과정으로 x0으로 부터 x1:T가 생성되는 과정을 조건부 확률의 곱으로 표현한다.
이 과정을 통해서 확률적으로 x0 -> xT를 만든 다음, 이걸 반대로 학습해서 다시 깨끗한 이미지 x0을 복원하는 과정을 학습하게 된다.

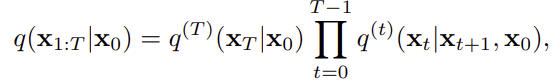
다음으로 아래의 수식을 보기 이전에 ELBO에 대해 알아보자.
ELBO는 Likelihood를 최대화하기 위한 최적화 대상이다.
확산 모델은 어떤 데이터 x가 나올 확률 log(pθ(x))를 최대화하려고 한다.
하지만, log(pθ(x))는 복잡해서 계산이 불가능하다.
그래서 이 값을 하한선으로 근사해서 최적화하기 위한 수단이 ELBO!

즉 ELBO는 복잡한 확률 계산을 피하기 위해, 학습 가능한 근사 지표로, 모델이 진짜 데이터를 얼마나 잘 설명하는지를 측정하고 최적화하는 역할이다.

DDPM에서는 이 ELBO가 아래와 같이 간단한 형태의 Denoising autoencoder loss로 바뀐다.
아래의 수식은 다음과 같은 의미를 갖는다고 생각하면 될 것같다.
"각 단계 t에서 노이즈가 낀 xt를 보고, 원래의 깨끗한 이미지 x0을 예측하는 fθ()를 학습한다."

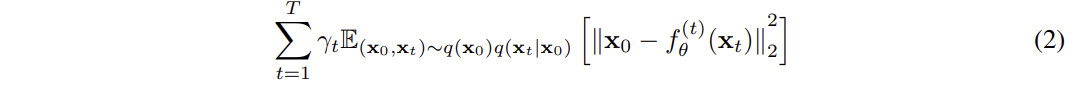
Denoising Diffusion Restoration Model

그럼 이제 본격적으로 DDRM에 대해 알아보자.
앞서 언급했듯이 비지도 방식은 다양한 문제에 적용할 수 있지만, 비효율적이라는 단점이 있고,
지도 방식은 효율적이지만 특정 문제에만 대응할 수 있다는 단점이 있다.

이 딜레마를 해결하기 위해 DDRM은 선형 역문제에서 효율적이고 일반적인 복원을 목표로 만든 Diffusion 기반 restoration 프레임워크이다.
기존의 DDPM은 y와 같은 관측값 없이 무작정 이미지를 생성하지만, DDRM은 관측된 y를 조건으로 넣어 복원 결과를 만든다.

Variational Objective for DDRM

DDRM도 기존 DDPM처럼 noise가 낀 상태은 x_T로 부터 깨끗한 이미지 x_0으로 가는 Markov chain이다. 단, 관측값 y를 조건으로 넣는 것이 핵심 차이이다.
즉, 각 단계의 샘플링이 y에 의존하게 되어, 복원 과정에 y를 반영할 수 있게 해준다.

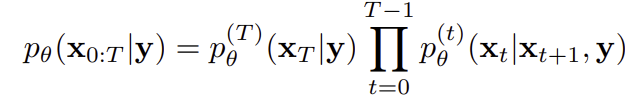
학습을 위해서는 학습용 분포 즉 noising 분포q도 정의해야 한다.
수식은 아래와 같다.
이러한 구조는 ELBO(Evidence Lower Bound)최적화를 가능하게 한다.

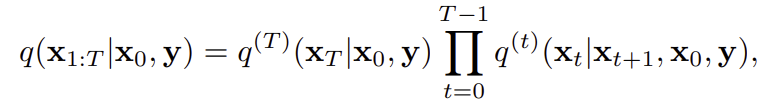
이와 같이 DDRM은 기존 DDPM의 구조를 유지한 채, 관측값 y를 조건으로 넣어 효율적이고 일반적인 역문제 복원을 가능하게 해주는 unsupervised diffusion 기반 모델이다.

A Diffusion Process for Image Restoration

DDRM은 spectural space에서 diffusion 과정을 설계한다.
왜냐하면 Spectural domain에서는 어떤 성분은 H에 의해 보존되고(정보가 있음),
어떤 성분은 H에 의해 완전히 날아가기 때문에 (정보가 없음) 이 각 경우에 따라 상황을 다르게 설계해주기 위함이다.

이를 위해 우선 SVD(Single Value Decomposition)로 분해를 해주는데 수식은 아래와 같다.

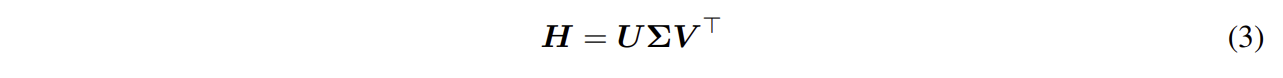
SVD (특이값 분해): 임의의 행렬 H를 3개의 행렬 곱으로 분해하는 방법
U: y를 표현
Σ: Singular value(정보가 있는/없는 방향 구분 가능
V: 원본 x를 표현

이와 같이 SVD분해를 통해 도출된 Σ의 성분 값을 통해 우리는 관측된 정보의 신뢰도를 얻어낼 수 있다.
이 신뢰도 값에 따라 해당 논문에서는 아래와 같이 3가지의 경우로 나누어 설계하였다.

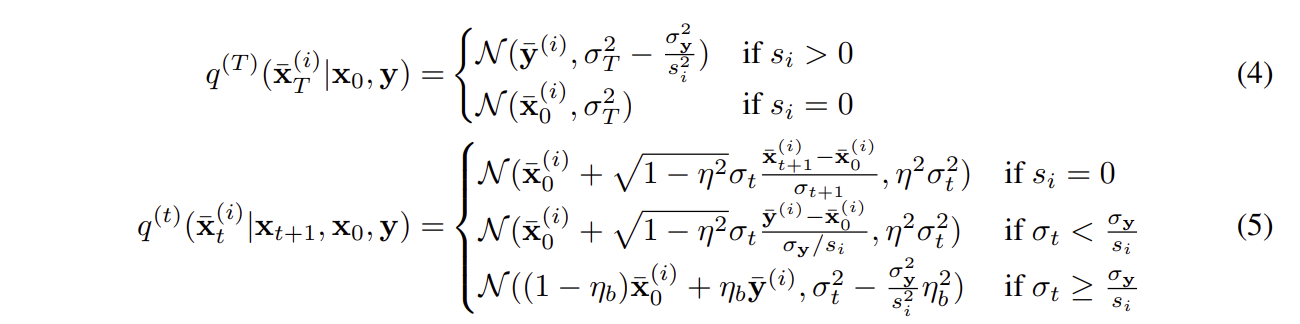
1. s_i=0 (해당 성분 정보가 y에 없음)

• 일반적인 unconditional diffusion처럼 수행
• 즉, 초기 x0에서 노이즈만 넣는 표준 diffusion
• 복원 과정에서는 pure generation 필요

2. s_i>0 (해당 성분 정보가 y에 있음)
   1. σ_t < (σ_y)/(s_i): 실제 관측 데이터 y에 들어있는 noise가 더 큼
      • 관측된 정보 y의 신뢰도가 낮음
      • 그래서 x_0의 예측값을 중심으로 sampling
   2. σ_t > (σ_y)/(s_i): 우리가 t시점에서 사용하는 noise가 더 큼
      • 관측된 정보 y의 신뢰도가 더 높음
      • 측정값 y를 그대로 신뢰

Proposition 1. Gaussian Marginals 보장

이 복잡한 구성에도 불구하고 각 시간 t에서의 분포는 아래의 식을 만족한다.
즉 기존 DDPM의 조건부 분포와 동일한 marginal 구조를 유지한다는 것이다.

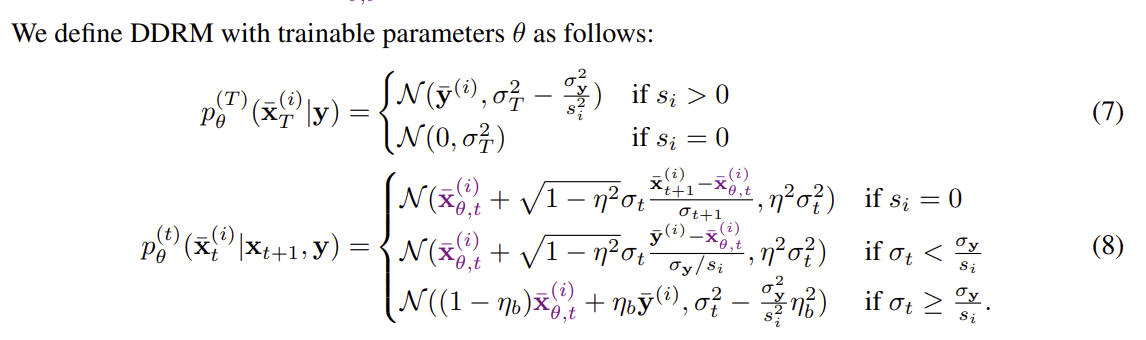
그럼 이제 Reverse Process를 보자.
이도 위의 noising과정처럼 경우의 수가 나뉘어져 있다.

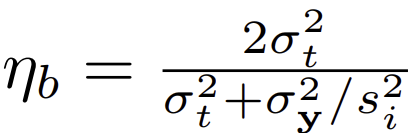
식이 매우 유사한 것을 확인할 수 있는데,
이는 q의 구조에서 x0이 (x_0)^의 꼴로만 바뀐 것이다.
**x_0은 ground truth이지만 sampling 단계에는 이 값이 없기 때문에 모델이 예측한(x_0)^ = fθ()를 사용**하는 것이다.

"Learning" Image Restoration Models

DDRM은 어떻게 새로 모델을 학습하지 않고도 다양한 Restoration 문제에 적용될 수 있을까?

기존에는 복원 문제(Blurring, Inpainting, ...)마다 모델을 다시 학습해야 하는 번거로움이 있었다.
즉 p()와 q()가 각각 생성 모델과 분포를 나타내고, 이에 기반해 ELBO를 최대화하는 방식으로 학습했는데, 이는 각 복원 문제마다 즉 H, σy가 다를 때마다 새롭게 학습해야 한다.
이러한 방법은 실용적이지 않고, 유연성이 떨어진다.

이에 DDRM은 미리 학습된 DDPM모델을 그대로 활용할 수 있도록 한다.

이는 아래의 Theorem을 통해 기존 DDPM모델이 DDRM 문제의 최적해와 같을 수 있다는 이론적 보장을 제시한다.

Theorem 2

• 조건
  - 각 timestep별 모델 가중치가 서로 공유되지 않음 (fθ^(t) != fθ^(t'))

  • η = 1이고, ηb는 다음처럼 설정할 경우
    

• 결과
  - DDRM의 ELBO는 DDPM의 손실 함수와 같은 형태로 표현 가능

  • 즉 DDPM을 새로 학습하지 않고도 DDRM 복원 문제에 적용할 수 있음

이 theorem은 아래와 같은 의미를 지닌다.

1. 다양한 복원 문제(선형 역문제 H와 측정 노이즈 σy가 다른 경우)에 대해
   • DDPM을 새로 학습할 필요 없이, 이미 학습된 모델을 활용해 복원할 수 있음
   • 단지, 복원에 필요한 행렬 H의 SVD만 바꿔주면 됨
2. 이는 DDPM을 단일 범용 restoration model로 사용할 수 있게 해 줌.

SVD를 바꾼다?
H는 복원 문제마다 다르다.
예를 들어 Inpainting에서 H는 픽셀 몇 개만 남기고 나머지는 0인 Sparse 행렬이고, super-resolution에서 H는 Downsampling 행렬이다.
그래서 복원하려는 문제마다 H 자체가 다 다르고 그에 따라 SVD가 바뀐다.
그래서 여기서 말하는 "SVD를 바꾼다"라는 말의 의미는 "복원하려는 Inverse problem이 바뀔 때마다 해당 문제의 H에 대해 새로운 SVD를 계산해 적용한다"라는 뜻이다.

Accelerated Algorithms for DDRM

Diffusion model은 느리다.
기본적으로 DDPM이나 DDIM 모델들은 1000step 정도 학습을 한다.
즉 복원하기 위해 이걸 역으로 따라가야 하므로 1000번의 noise 제거를 수행한다는 것이다.
이러한 상황을 많은 NFE(Number of Function Evaluations)가 필요하다고 표현한다.

이러한 문제를 해결하기 위해 DDRM은 Skip하면서 빠르게 복원하는 방법을 채택한다.
이게 무슨 말이냐면 복원 시에 sampling step을 적게 사용한다는 것이다.
기존에 학습은 1000step이라하면 샘플링은 50step만 써도 괜찮게 복원한다는 것이다.

이러한 방법을 Skip sampling이라고 한다.

Memory Efficient SVD

SVD는 메모리를 많이 쓴다는 문제점이 있다.

이 계산은 고해상도 이미지일 수록 커지는데, 이러한 문제를 해결하기 위해 DDRM에서는 H의 특수성을 활용해 메모리 복잡도 Θ(n²)을 Θ(n)으로 줄였다.
특수성을 활용했다는게 무슨 뜻일까?
Appendix D에 구체적으로 나와있지만 세부적으로 하나하나 보진않을 거구

예를 들어 Denoising과 같은 경우, 잡음을 제거하는 것이지 때문에 H=I(항등 행렬)로 둔다. 따라서 이 상황의 경우 복잡도는 Θ(1).
Colorization의 경우, 회색->RGB로 변환하는 것이기 때문에 H는 RGB평균 즉 1/3, 1/3, 1/3 이런 행렬일 것이다. 이 경우 복잡도는 Θ(n).
Inpainting의 경우 픽섹을 부분 선택하는 꼴의 H를 가지고 있을 것이므로 메모리 복잡도 Θ(n).

이와 같은 Degrade연산의 특징에 따라 H를 적절히 선택하여 사용한다는 것이다.

이러한 방식 덕분에 각 SVD연산은 메모리 복잡도 Θ(n)만으로도 구현 가능하다.

Related Work

해당 파트에서는 기존 연구들의 한계점과 DDRM의 차별점을 보인다.
기존의 비지도 학습 기법에는 PnP, RED, ADMM 이 있다.
이들은 denoiser를 반복 최적화 과정의 한 단계로 사용하여 이미지 denoise -> 다시 복원 측정치에 맞춤 -> denoise ... 이런 방식으로 반복한다.

흔히 알려진 GAN 기반 접근은 Latent space에서 측정치와 유사한 이미지를 찾는다. 그러나 해당 방법을 얼굴처럼 특정 클래스에서는 잘 되지만, ImageNet과 같은 다양한 이미지에는 약하다.

이에 diffusion based method가 이러한 inverse problem에 쓰이기 사용되었다.
Diffusion based 방법은 noise가 심한 경우에도 이미지 복원이 가능하다는 장점이 있지만, 수백~수천번의 반복이 필요하여 매우 느리다는 단점이 있다.

이에 비해 DDRM은 아래와 같은 장점들을 가진다.

• Diffusion based model임에도 훨씬 빠름
• 변분 추론(variational inference)에서 아이디어를 가져와서, 문제 특화된 비평형 (non-equilbrium) 업데이트 규칙을 사용
• 기존 diffusion model들이 보통 동일한 일반적인 업데이트만 쓰는 데 반해, DDRM은 문제에 맞춘 업데이트로 성능을 높임

이 외에도 ILVR이나 Score-based inverse solver들과 달리 노이즈가 있는 이미지에 대해서도 처리가 가능하다는 차별점을 갖는다.

결론적으로 DDRM은 다양한 Inverse problem을 unsupervised 학습 방식으로, 기존 diffusion model보다 훨씬 빠르게 noise가 있는 관측치까지 처리 가능한 방법이다.

Non-equilbrium(비평형적) 업데이트?
기존의 일정한 규칙으로 noise를 줄이며 복원하지 않고, 관측된 degraded 이미지와 그 조건(H)을 활용해서 빠르게, 목표 이미지에 수렴하도록 특정 규칙에 따라 업데이트하는 방식

Experiments

Experimental Setup

CelebA-HQ, LSUN, ImageNet 등에서 학습된 기존 확산 모델을 사용하고, FFHQ나 인터넷 이미지 등으로 테스트했다.
일부 ImageNet 모델은 클래스 조건이 필요해서 DDRM-CC로 구현했다

각 inverse problem에 대해 아래와 같이 수행하였다.

• Super resolution: 블록 평균 필터로 축소
• Deblurring: 9x9 kernel 로 blurring하고 특이값을 임계값 이하로 제거
• Colorization: RGB 평균으로 회색화
• Inpainting: text나 무작위 마스킹
• Noise: 선택적으로 Gaussian nosie

모든 실험은 픽셀값 [0,1] 범위에서 수행했고, 사전 학습된 1000step 모델의 균일한 time step 스케줄을 사용하고, DDRM은 매우 적은 반복만으로 높은 성능을 달성하였다.
실험 결과를 살펴보자.

Quantitative Experiments

해당 파트에서는 DDRM에 대해 정량적 평가를 수행한다.

데이터셋 및 평가지표: ImageNet(256x256)을 중심으로 PSNR, SSIM, KID 지표 사용
비교 대상: Unsupervised model(RED, DGP, SNIPS)

결과는 아래와 같다.

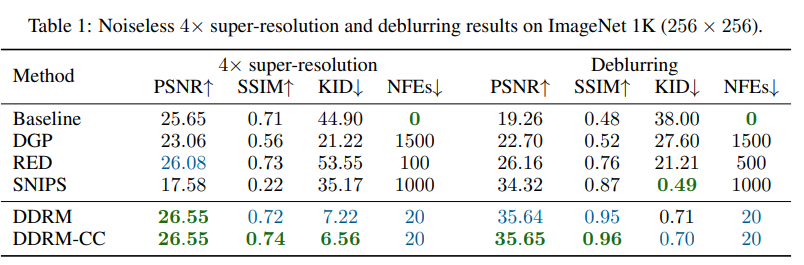
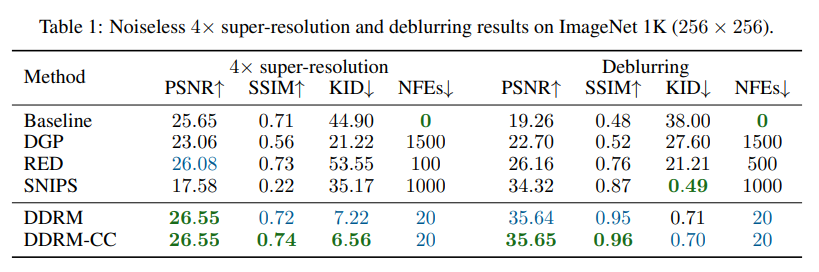
Table 1은 DDRM은 단 20 step으로 대부분의 문제에서 기존 모델보다 뛰어난 성능을 보인다.
SNIPS가 Deblurring에서 KID 성능이 소폭 앞서지만 50배 더 많은 계산량이 필요하다.

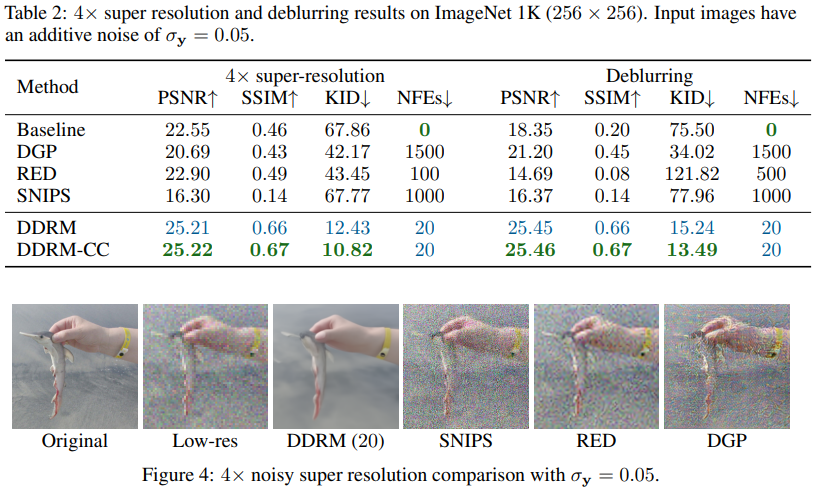
Table 2는 측정값에 noise가 있는 경우에 대한 결과이다.
이때 DDRM의 이점이 더 뚜렷하게 보이는 것을 확인할 수 있다.

Qualitative Experiments

다음은 DDRM의 실제 restoration 결과이다.
논문에서는 해당 고품질의 복원 결과를 생성한다고 언급하고 있다.

또한 DDRM은 Posterior sampling algorithm이기 때문에, 동일한 입력에 대해 아래와 같이 여러 개의 출력 결과를 생성할 수 있다.

아래는 ImageNet이 아닌 다른 데이터셋(USC-SIPI)의 이미지에 대해서도 성공적으로 복원해내는 결과를 보여준다.

Conclusion

DDRM은 Unsupervised 학습 기반의 선형 inverse problem 해결 방법으로 소수의 step만으로도 super-resolution, denoising, deblurring, inpainting, colorization 등의 다양한 이미지 복원 작업에서 고성능을 보인다.

기존 diffusion 기반 방법들보다 훨씬 빠르고 효율적이며, 학습 데이터 분포 밖의 일반 자영 이미지에도 잘 작동한다. 특히, 강한 noise 상황에서도 posterior 분포에서 효과적으로 샘플링할 수 있는 첫 unsupervised 방법으로 평가된다.

마무리

이번에 DDPM 발표를 준비하면서 여러 논문을 찾아보다가 발견한 논문이다.
내 연구에 보석같은 논문인데, 앞으로 연구하면서 볼 일이 많을거같아서 정리하게됐다.

세부적으로 하나하나 읽어보니 조건부 확률에 관측치를 조건으로 하나 추가해준다는 아이디어가 참 단순하면서도 성능이 잘 나오니 신기하다.

또 의외로 ImageNet의 성능 지표 테이블을 살펴보면 DDRM과 DDRM-CC의 PSNR, SSIM 면에서의 성능 차이가 크지않은데, 그렇다면 Class label이 크게 관여하지 않는다는 거같으면서도 DDRM이 이 정보를 크게 활용하지 못하나 라는 생각이 들기도 했다. 이러한 측면에서 Diffusion model은 연구할 부분이 참 많은 분야인 것같다.

ㅎㅎrestoration쪽 연구하시는 분들이면 읽어보기 좋은 논문인 것같다. 재밌었당~😊