99클럽 코테 스터디
오늘의 문제는 프로그래머스 기준 오류가 있습니다. (틀려도 통과됨)
오늘의 문제인 이중 우선순위 큐는 작년에 백준에서 풀어본 문제이다. 그 때는 heapq 모듈을 사용하지 않고 리스트만으로 구현해보았는데, 굉장히 힘들었던 기억이 난다. 지금 다시 풀어보니 놀라우리만치 간단하게 풀 수 있었는데, 그래도 꽤 많이 성장했구나 하는 점을 느낄 수 있었다.
...라고 생각했는데 알고보니 틀왜맞 이었다. 틀려먹은 코드로도 통과가 되는 것이었다. 문제점을 찾는 데는 조금 걸렸고, 다시 해결하는 방법 자체는 쉬웠다.
프로그래머스의 해당 문제는 테스트케이스가 아주 부족하므로, 백준의 문제를 푸는 것이 낫겠다.
1번 문제 이중 우선순위 큐 : https://school.programmers.co.kr/learn/courses/30/lessons/42628
백준의 이중 우선순위 큐 : https://www.acmicpc.net/problem/7662
출처 : 프로그래머스, 백준
1번 문제 이중 우선순위 큐
풀이 접근
힙을 두 개 관리한다. 하나는 최소힙, 하나는 최대힙으로 하고, 최솟값을 삭제할땐 최소힙에서 빼고, 최댓갑을 삭제할땐 최대힙에서 뺀다. 이러다 보면 중복이 생길 수 있으므로 이중 우선순위 큐에 아무 원소도 남지 않을 때(큐의 길이를 관리하면 알 수 있다)는 그냥 양 쪽 힙을 다 비워버린다.
이렇게 풀면 틀렸다. (프로그래머스에선 통과된다)
왜 틀린지는 아래 코드 설명에 반례가 있다...
틀린 코드(Python3, 통과, 최대 0.06ms, 10.5MB, 백준에서는 틀렸습니다)
!!!주의!!! 틀린 코드인데 프로그래머스는 통과됨
아래 코드는 프로그래머스에서는 가볍게 통과가 된다. 근데 제출하자마자 이상함을 느낄 수 있는데, 테케 개수도 적거니와 operation의 길이가 100만이래놓고 최대 0.06초밖에 걸리지 않는다. 테케가 아주 작고 적은 것이다.
아니나 다를까, 해당 코드를 (제출 형식을 맞춰서) 백준의 같은 문제에 넣어보면 가볍게 틀렸습니다가 뜬다. 아래 코드의 반례는 다음과 같다.
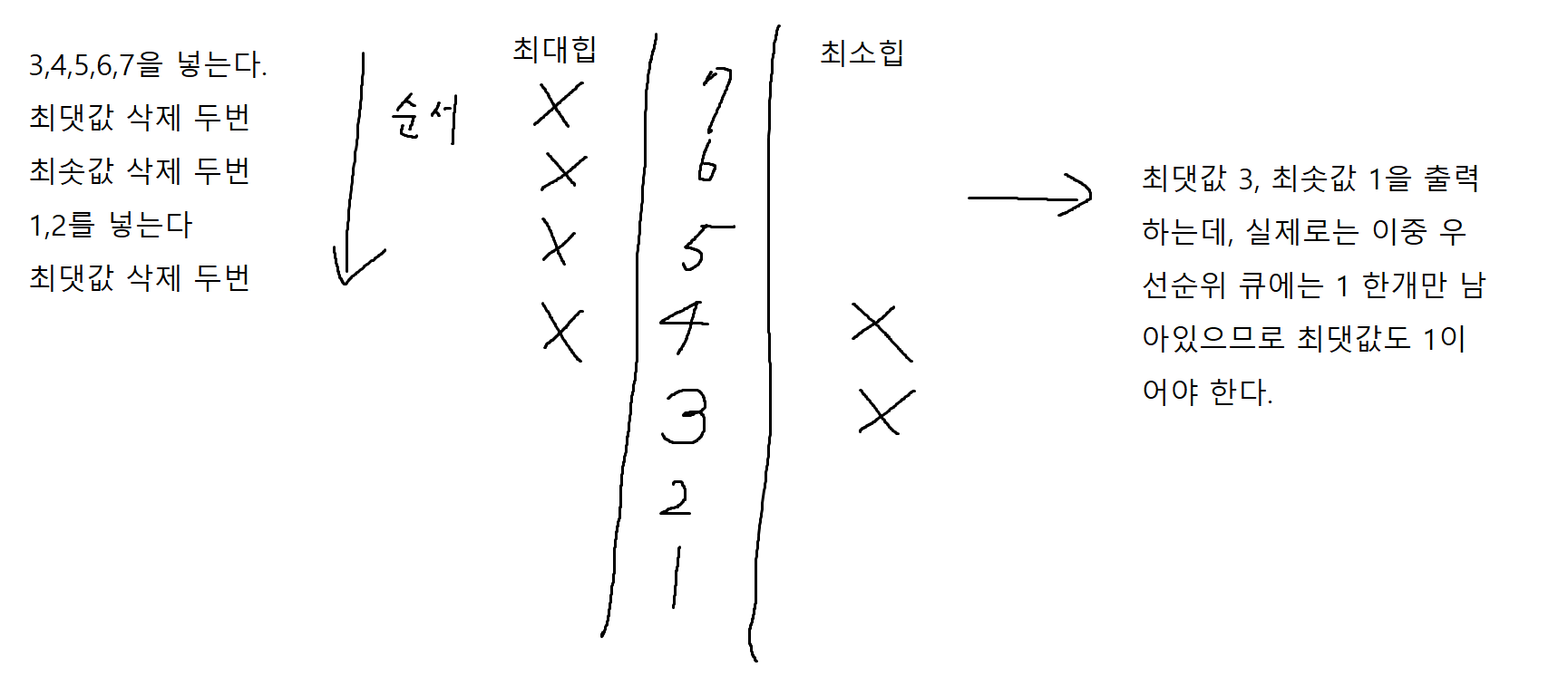
최대힙 최소힙을 따로 관리할 때는, 넣고 빼는 순서에 따라, 이미 뺀 원소를 또 빼게 될 수도 있음에 유의한다.
import heapq
def solution(operations):
heap_min = []
heap_max = []
heap_length = 0
for i in range(len(operations)):
op, num = operations[i].split()
num = int(num)
if op == 'I':
heapq.heappush(heap_min, num)
heapq.heappush(heap_max, -num)
heap_length += 1
elif heap_length <= 1:
heap_min.clear()
heap_max.clear()
heap_length = 0
elif num == 1:
heapq.heappop(heap_max)
heap_length -= 1
else:
heapq.heappop(heap_min)
heap_length -= 1
if not heap_length:
return [0,0]
answer = [-heapq.heappop(heap_max), heapq.heappop(heap_min)]
return answer다시 풀이 접근
최소힙 최대힙 뿐만 아니라 실제로 어떤 원소가 들어있는지도 관리한다(이 관리하는 자료구조 자체를 매번 정렬하거나 할 순 없지만, 있는지 없는지 확인 정도는 시간복잡도를 크게 해치지 않고 할 수 있다).
다만, 파이썬의 기본 자료구조 중에 딱 들어맞게 쓸 수 있는 건 dictionary 하나 뿐인 것으로 보인다.
why?
- 중복 원소가 들어올 수 있으므로, set 자료구조로 날먹하기는 힘들다.
- list에서 특정 값을 없애려면 O(n)이므로 list 자료구조도 쓸 수 없다.
개정된 코드(Python3, 통과, 최대 0.09ms, 10.6MB)
백준에서는 PyPy3, 맞았습니다!, 메모리 296432KB, 시간 2572ms
아주 세련된 방법으로 변수와 자료를 관리한 것 같진 않다.
그래도 값을 한쪽에서만 삭제할 때에, 그게 실제로 아직 존재하는 값인지 확인하는 것은 dictionary 자료구조로 정확히 처리하였다.
이미 삭제된 값이 남아있을 때는, 실제 존재하는 값을 pop할때까지 while문으로 돌려준다.
마지막에 answer를 반환할 때도 마찬가지 과정을 거쳐준다.
import heapq
def solution(operations):
heap_min = []
heap_max = []
queue = {}
heap_length = 0
answer = []
for i in range(len(operations)):
op, num = operations[i].split()
num = int(num)
if op == 'I':
heapq.heappush(heap_min, num)
heapq.heappush(heap_max, -num)
if num in queue:
queue[num] += 1
else:
queue[num] = 1
heap_length += 1
elif not heap_length:
pass
elif num == 1:
while True:
deleted = -heapq.heappop(heap_max)
if queue[deleted]:
queue[deleted] -= 1
break
heap_length -= 1
else:
while True:
deleted = heapq.heappop(heap_min)
if queue[deleted]:
queue[deleted] -= 1
break
heap_length -= 1
if not heap_length:
return [0,0]
while True:
maximum = -heapq.heappop(heap_max)
if queue[maximum]:
answer.append(maximum)
break
while True:
minimum = heapq.heappop(heap_min)
if queue[minimum]:
answer.append(minimum)
break
return answer아래는 백준 코드이다. 입출력 방식의 차이만 있고 코드는 기본적으로 같다.
import heapq, sys
input = sys.stdin.readline
t = int(input())
for _ in range(t):
k = int(input())
heap_min = []
heap_max = []
queue = {}
heap_length = 0
for i in range(k):
op, num = map(str, input().strip().split())
num = int(num)
if op == 'I':
heapq.heappush(heap_min, num)
heapq.heappush(heap_max, -num)
if num in queue:
queue[num] += 1
else:
queue[num] = 1
heap_length += 1
elif not heap_length:
pass
elif num == 1:
while True:
deleted = -heapq.heappop(heap_max)
if queue[deleted]:
queue[deleted] -= 1
break
heap_length -= 1
else:
while True:
deleted = heapq.heappop(heap_min)
if queue[deleted]:
queue[deleted] -= 1
break
heap_length -= 1
if not heap_length:
print('EMPTY')
else:
while True:
maximum = -heapq.heappop(heap_max)
if queue[maximum]:
break
while True:
minimum = heapq.heappop(heap_min)
if queue[minimum]:
break
print(maximum, minimum)참고용 코드(2023.02.16 백준, PyPy3, 맞았습니다!, 579884KB, 17280ms)
작년에 며칠에 걸쳐 풀었던 코드이다. 엄청 길다.
이중 힙을 실제로 노트에 끄적여서 자료구조의 형태로 만들고, 리스트의 인덱스를 이용해서 실제로 구현했다. 통과에 17초나 걸렸지만 heapq를 안 쓰고 실제로 구현해서 풀었다는 데에 의의를 두었다. 파이썬 계열에서 가장 빠른 게 1.7초이니 heapq를 안 쓰고 10배 차이면 그렇게까지 못한 것도 아니기도 하고.
근데 지금 다시 보면... for문 안에 함수를 정의하다니 정말 레전드가 아닐 수 없다. 함수만 for문 밖에 정의했어도 이렇게 짜치진 않았을 것이다. 그래도 이 문제를 풀 때 코딩 응애였다는 점을 감안하여 과거의 나를 용서하기로 했다.
import sys
t = int(input())
for _ in range(t):
k = int(input())
heap = []
graph_upward = {}
graph_downward = {}
def heapify_upward(n):
global heap
if n not in graph_upward:
return
up = graph_upward[n]
if not up:
return
up1 = up[0]
if len(up) == 1:
if heap[n] < heap[up1]:
heap[n], heap[up1] = heap[up1], heap[n]
heapify_upward(up1)
return
return
up2 = up[1]
if heap[up1] > heap[up2]:
if heap[n] < heap[up1]:
heap[n], heap[up1] = heap[up1], heap[n]
heapify_upward(up1)
return
return
if heap[n] < heap[up2]:
heap[n], heap[up2] = heap[up2], heap[n]
heapify_upward(up2)
return
return
def heapify_downward(n):
global heap
if n not in graph_downward:
return
do = graph_downward[n]
if not do:
return
do1 = do[0]
if len(do) == 1:
if heap[n] > heap[do1]:
heap[n], heap[do1] = heap[do1], heap[n]
heapify_downward(do1)
return
return
do2 = do[1]
if heap[do1] < heap[do2]:
if heap[n] > heap[do1]:
heap[n], heap[do1] = heap[do1], heap[n]
heapify_downward(do1)
return
return
if heap[n] > heap[do2]:
heap[n], heap[do2] = heap[do2], heap[n]
heapify_downward(do2)
return
return
def graph_add(n):
global graph_upward
global graph_downward
if not n:
return
if n == 1:
graph_downward[0] = [1]
graph_upward[1] = [0]
return
if bin(n + 2)[3] == '0':
up = n // 2 - 1
down = n // 2 - 1 + 2 ** (len(bin(n + 2)) - 5)
graph_upward[n] = [up]
graph_downward[n] = [down]
if graph_upward[down][0] == up:
graph_upward[down][0] = n
graph_downward[up][0] = n
return
graph_upward[down].append(n)
graph_downward[up].append(n)
return
down = n // 2 - 1
up = n - 2 ** (len(bin(n + 2)) - 4)
graph_upward[n] = [up]
graph_downward[n] = [down]
graph_downward[up][0] = n
if graph_upward[down][0] == up:
graph_upward[down][0] = n
return
graph_upward[down][1] = n
return
def graph_remove(n):
global graph_upward
global graph_downward
if not n:
return
if n == 1:
del graph_downward[0]
del graph_upward[1]
return
if bin(n + 2)[3] == '0':
up = graph_upward[n][0]
down = graph_downward[n][0]
del graph_upward[n]
del graph_downward[n]
if graph_upward[down][0] == n:
graph_upward[down][0] = up
graph_downward[up][0] = down
return
graph_upward[down].pop()
graph_downward[up].pop()
return
up = graph_upward[n][0]
down = graph_downward[n][0]
del graph_upward[n]
del graph_downward[n]
graph_downward[up][0] = down
if graph_upward[down][0] == n:
graph_upward[down][0] = up
return
graph_upward[down][1] = up
return
for _ in range(k):
c, x = map(str, sys.stdin.readline().strip().split())
x = int(x)
if c == 'I':
n = len(heap)
graph_add(n)
heap.append(x)
heapify_downward(n)
heapify_upward(n)
else:
n = len(heap) - 1
if len(heap) > 2:
if x == -1:
heap[0] = heap[-1]
heap.pop()
graph_remove(n)
heapify_downward(0)
else:
heap[1] = heap[-1]
heap.pop()
graph_remove(n)
heapify_upward(1)
elif len(heap) == 2:
if x == -1:
heap.pop(0)
else:
heap.pop()
graph_remove(1)
elif heap:
heap.pop()
if heap:
if len(heap) > 1:
print(heap[1], heap[0])
else:
print(heap[0], heap[0])
else:
print('EMPTY')
