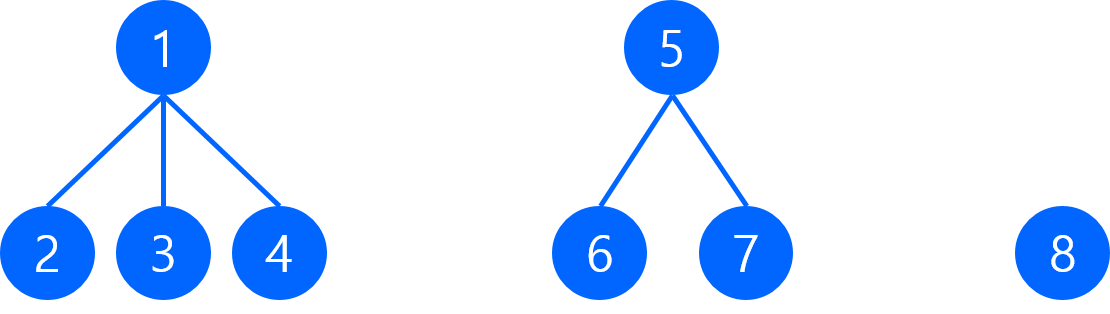
Disjoint Set이란?
Disjoint Set(서로소 집합)은 공통 원소가 없이 "상호 배타적인" 부분집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조이다.
정의 기능을 구현하기 위해 밑 세 가지 연산을 구현해야 합니다.
- 초기화 : N개의 원소가 각각의 집합에 속하도록 초기화한다.
- Union(합치기) 연산 : 두 원소가 주어졌을 때 두 원소가 속한 집합을 하나로 합친다.
- Find(찾기) 연산 : 어떤 원소가 주어졌을 때 해당 원소가 속한 집합을 반환한다.
여기서 Union과 Find에 대한 구현(알고리즘)을 묶어서 유니온 파인드라고 부른다.
유니온 파인드란?
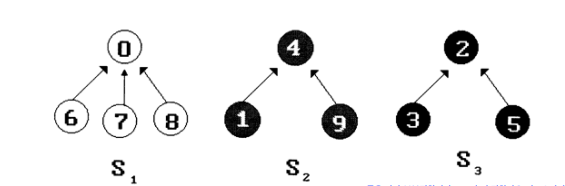
유니온 파인드는 Disjoint Set의 Union과 Find연산을 구현하는 알고리즘이다.
Union Find는 크루스칼의 MST 알고리즘을 효과적으로 구현할 수 있게 해준다. (사이클 판정)
-> Union 시도를 해서 만약 Union하려는 두 원소의 대표원소가 같다면 같은 집합 내에서 합연산을 시도한 것이다. 이는 사이클 발생을 의미한다.
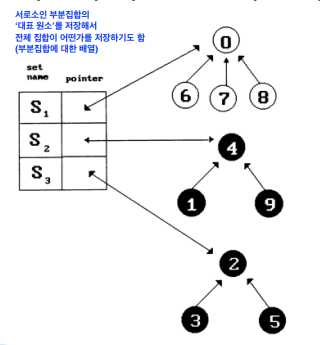

유니온 파인드는 각 집합을 대표원소를 root로 하는 트리를 이용하여 표현한다. 그리고 배열 하나로 표현할 수 있는 이유는 각 원소가 가진 포인터만을 기록해주면 되기 때문이다.
구성
유니온 파인드는 이름 그대로 두 가지 연산을 가진다.
- union(x, y) : 원소 x가 속한 부분집합과 원소 y가 속한 부분집합의 합집합을 구한다.
- find(x) : 원소 x가 속한 부분집합을 찾는다. 보통 x가 속한 부분집합의 대표원소를 반환한다.
단순한 구현
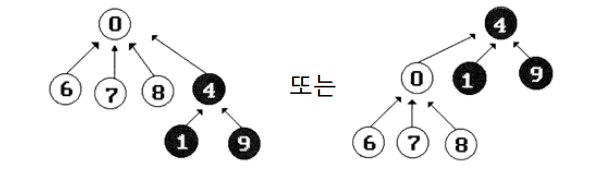
Union(x, y)은 x원소를 y원소의 자식으로 연결하거나 y원소에 x원소를 연결해주면 된다.
find(x)는 x에서 시작해서 루트에 도달할 때까지 계속 부모 노드를 찾아 올라간다.
문제점
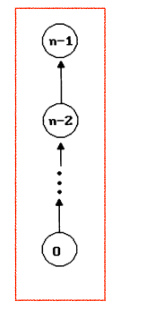
그러나 이는 편향 트리가 될 수 있다. 즉 union은 O(1)이 보장되지만, find는 O(n)이 걸린다.
Find를 위한 Union의 최적화
Union으로 트리가 구성되기에 트리의 높이가 줄도록하면 결과적으로 find시간을 줄일 수 있다.
결론부터 말하자면, union by size, union by rank 두 가지 방법으로 트리의 높이는 (log_2 n)으로 줄일 수 있다.
즉 find(x) 연산이 O(log n)이 된다.
Union by rank
rank는 트리의 높이와 같은 의미를 가지는데, 나중에 find연산의 최적화 과정에서 rank는 높이와 달라질 수 있어 높이와는 구분된 표현을 가진다. find 최적화에서 좀 더 알아보기로 하고 일단 Union by rank를 확인해보자.
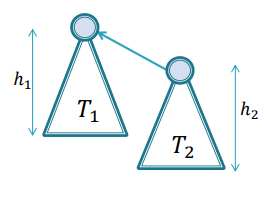
집합을 트리로 보기로 했으므로, 합집합을 연산할때 서브 트리 두 개를 하나의 트리로 만드는 것을 생각해보자.
만약 h1 > h2라면 위 연산의 결과 트리의 높이는 h1임이 보장된다. h2 입장에서 높이가 하나 달라지기 때문이다.
이런 원리로 rank가 다르다면 큰 쪽에 작은 트리를 붙이게 된다. 이때 최종 rank는 큰쪽을 따라가게 된다.
단 rank가 같은 트리를 유니온하면 +1한 rank를 최종적으로 가지게 된다.
즉 이런 원리로 높이가 log_2 n 이하가 된다.
Union by size
노드의 개수가 큰 쪽에 작은 쪽을 붙이는 방식이다. 이를 가중법칙이라고도 하는데 수학적 귀납법에 의해 증명된다. (생각보다 어렵지 않다.)
아무튼 최종적으로 마찬가지로 log_2 n 이하의 높이가 보장된다.
메모리 팁
두 연산 모두 노드의 개수와 rank를 저장해야함으로 마치 배열이 하나 더 필요할 것 같다.
그러나 배열에서 포인터가 음수를 가르킬 일은 없고 rank와 노드 개수도 음수나 0이 될 일은 없으므로, rank나 높이를 음수로 치환해서 저장해두고 사용하면 배열 하나만으로 구현 가능하다!
https://8iggy.tistory.com/157
해당 블로그에 결과를 보면 음수가 나오는데 이런 방법을 사용한 것이다.
find 경로 압축(path compression)
위 최적화로 O(log n)의 시간복잡도가 되었다. 이 find를 더 빠르게 해보자.
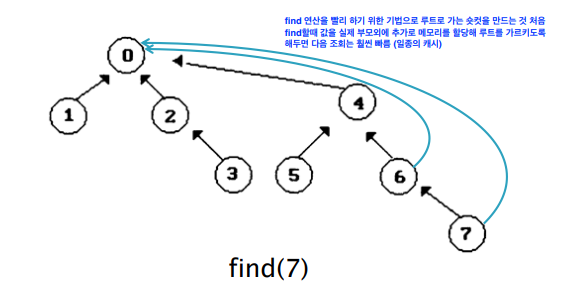
find가 호출되었을때 거쳐가는 원소들의 포인터를 대표원소를 가져와 대표원소를 가르키도록 갱신하는 것이다.
이를 유니온 연산 최적화와 합하면 최종적으로 O(알파(n)) 측 아커만 역함수가 된다.
이는 거의 상수로 볼 수 있다. O(1)
즉 해당 방식을 사용할때 Union by rank를 택했다면 트리의 높이가 달라질 수 있다. 그러나 이를 갱신하는건 시간복잡도 손해가 발생한다. 즉 rank라는 별도의 수를 둠으로서 따로 갱신하지 않는다.
자바로 구현 (Union by size + path compression)
public class Main {
static int[] parents = new int[5]; // 0이상의 자연수는 부모의 주소, 음수는 대표원소(집합의 원소 개수)
private static void union(int x, int y) {
int xp = find(x);
int yp = find(y);
if (parents[xp] > parents[yp]) { // Union by size : 음수이므로 y가 size가 큰 상황
parents[yp] += parents[xp]; // size 연산
parents[xp] = yp; // 포인터 옮기기
} else {
parents[xp] += parents[yp];
parents[yp] = xp;
}
}
private static int find(int x) {
if (parents[x] < 0) return x;
else {
parents[x] = find(parents[x]); // path compression
return parents[x];
}
}
public static void main(String[] args) {
// 초기화
for (int i = 0; i < parents.length; i++) {
parents[i] = -1;
}
union(0, 1);
union(1, 2);
union(2, 3);
for (int i = 0; i < parents.length; i++) {
System.out.print(parents[i] + " "); // -4 0 0 0 -1
}
System.out.println();
System.out.println(find(4)); // 4
System.out.println(find(3)); // 0
}
}자바 크루스칼 알고리즘 응용
import java.util.*;
class Solution {
int[] parents;
private int find(int x) {
if (parents[x] < 0) return x;
else {
parents[x] = find(parents[x]);
return parents[x];
}
}
private boolean union(int x, int y) {
int px = find(x);
int py = find(y);
if (px == py) return false; // 사이클
if (parents[px] < parents[py]) {
parents[px] += parents[py];
parents[py] = px;
} else {
parents[py] += parents[px];
parents[px] = py;
}
return true;
}
public int solution(int n, int[][] costs) {
int answer = 0;
parents = new int[n];
// init
for (int i = 0; i < n; i ++) {
parents[i] = -1;
}
// 정렬
Arrays.sort(costs, (arr1, arr2) -> arr1[2] - arr2[2]);
// 순회
for (int[] cost : costs) {
if (union(cost[0], cost[1])) answer += cost[2];
}
return answer;
}
}https://school.programmers.co.kr/learn/courses/30/lessons/42861