제곱(power)은 컴퓨터에서 어떻게 하면 빠르게 구현할 수 있을까?

exponentiation(거듭제곱) 수학 정의

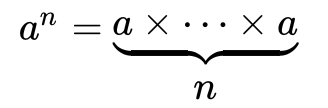
exponentitation은 base(밑)와 exponent(power)(지수)로 구성된다.

컴퓨터에서의 연산

구현 1 - 정의를 이용한 방법

가장 간단하게 exponentitation을 구현하는 방법은 정의에 따라 곱셈을 진행하는 것이다.
단순히 곱셈을 N번 진행하여 계산을 진행한다.

시간복잡도: O(N)

구현 2 - 연산법칙을 활용한 방법

a^n = (a^(n/2))^2

N거듭제곱을 구하는 과정에서 연산법칙에 따라 N/2를 거듭제곱한 값을 구한 후 이에 제곱을 취해 N을 계산하는 방법이 있다. 이는 분할 정복과 비슷한 방식으로 O(logN)시간에 빠르게 풀이 가능하다.

예시. 행렬의 빠른 거듭제곱

	// 행렬의 곱 연산
    private static long[][] cross(long[][] a, long[][] b) {
        long[][] result = new long[a.length][b[0].length];
        for (int i = 0; i < a.length; i++) {
            for (int j = 0; j < b[0].length; j++) {
                for (int k = 0; k < a[i].length; k++) {
                    result[i][j] += a[i][k] * b[k][j];
                }
            }
        }
        return result;
    }
	
    // 행렬의 거듭제곱 연산
    private static long[][] pow(long[][] base, long exp) {
        if (exp == 0) {
            return I;
        }
        if (exp == 1) {
            return base;
        }

        long[][] sqrt = pow(base, exp / 2);
        long[][] tmp = cross(sqrt, sqrt);
        return cross(tmp, pow(base, exp % 2));
    }

참고

https://ko.wikipedia.org/wiki/거듭제곱
https://www.rookieslab.com/posts/fast-power-algorithm-exponentiation-by-squaring-cpp-python-implementation