알고리즘 모음

2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)자기 자신을 제외한 2의 배수를 모두 지운다.남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)

GCD, LCM의 정의와 알고리즘을 알아보자

정렬 알고리즘들을 알아보자.

배열이 크기순으로 정렬되어 있을때 O(logN) 시간에 값의 위치를 탐색할 수 있는 알고리즘. 배열이 크기순으로 정렬되어 있기에 구역을 절반씩 나눠 원하는 값이 어떤 영역에 있는지 탐색을 반복해 위치를 특정한다.이분탐색 알고리즘은 크게 2가지 목적으로 사용할 수 있다.

꽤 다양하게 응용할 수 있는 4가지 알고리즘의 코드를 자바로 한번 구현해보았다. 모두 생각보다 직접 떠올리기 쉽지 않다. 순열 두 구현방식 모두 재귀를 사용하지만 장단점이 있다. 구현 1. swap (빠른 방법) 구글링 해보니 해당 방법을 좀 더 많이 사용하는

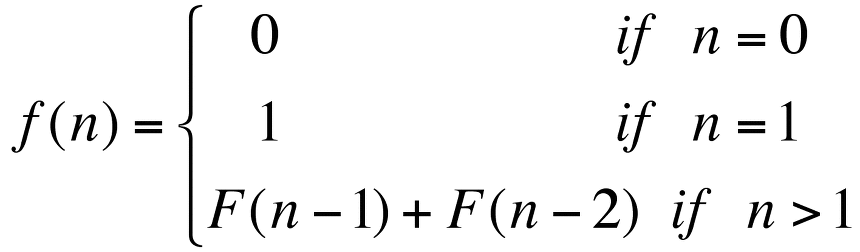
알고리즘을 세울 때 상당히 어려운 것이 다양한 조건의 점화식을 구성하는 것이다.점화식이란 수열의 각각의 항들간 관계를 표현한 식이다.동일한 부분문제로 큰 문제를 분해하는 것이 가능하다.가장 작은 단위의 해답 base(기저식)이 존재한다는 점이다. base와 동일 부분

공간복잡도가 눈에 띄게 제한적인 문제들도 있다. 이럴때 사용할 수 있는 비트연산을 활용한 비트 마스킹을 소개한다.

PS를 하다보면 값의 크기에 따라

누적합은 특정 구간내의 수열의 원소들의 집계를 구해야하는 문제에서 유용하게 사용될 수 있다.만약 쿼리형태로 특정 구간에 수열 원소들의 합을 구하는 명령이 들어온다. 이걸 각각 구한다면 O(n)이라는 상당히 비싼 비용이 들어가게 된다.누적합은 이런 합을 미리 계산해둠으로

삼성 DX 동계 알고리즘 강의를 듣다보니 처음듣는 알고리즘이 정말 많다. KMP, 라빈카프 등등.. 이런 알고리즘들을 잘 정리해둔 블로그가 있어 해당 블로그의 내용에 따라 공부해볼만한 알고리즘과 빈도를 정리해본다. 공부해야하는 알고리즘 two pointer 누적합 이

제곱(power)은 컴퓨터에서 어떻게 하면 빠르게 구현할 수 있을까? exponentiation(거듭제곱) 수학 정의 exponentitation은 base(밑)와 exponent(power)(지수)로 구성된다. 컴퓨터에서의 연산 구현 1 - 정의를 이용한 방법