소수
1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수
단일 소수 검사 - 검사식
단순히 for문을 돌면서 구할 수 있지만 그거보다는 유효하게 O(root(n))으로 줄일 수 있다. log만큼은 아니지만 꽤나 효율적이다. 만약 에라토스테네스의 체가 너무 느리거나 배열을 구성하기에 너무 큰 경우 고려할 수 있다.
private boolean isPrime(long v) {
if (v <= 1) return false;
for (long i = 2; i * i <= v; i ++) { // 핵심 i*i <= v
if (v % i == 0) return false;
}
return true;
}이는 약수의 대칭성을 이용한 것이다.

즉 root(n)을 기준으로 약수가 존재한다면 대칭 구조를 띄기에 절반만 검사하는 것이다.
i < v는 O(v)지만 i * i <= v로 O(root(v))로 개선되었다.
여러개의 소수 검사 - 에라토스테네스의 체
여러 수의 소수를 찾는 가장 효율적인 알고리즘
공간복잡도가 O(N)으로 찾으려는 소수의 크기가 중요하다. 최소 표를 구성하는데 O(N)의 시간복잡도가 소비되며 이후는 해당 범위내의 소수를 O(1)만에 판정할 수 있다. 마찬가지로 root(N)까지만 나눠보면 나머지에선 추가적인 합성수가 발생하지 않으므로 root(N)이하 까지만 반복문을 돌아도 된다.

// n+1만큼 할당
primeList = new ArrayList<Boolean>(n+1);
// 0번째와 1번째를 소수 아님으로 처리
primeList.add(false);
primeList.add(false);
// 2~ n까지 소수로 설정
for(int i=2; i<=n; i++ )
primeList.add(i, true);
// 2부터 ~ i*i <= n
// 각각의 배수들을 지워간다.
for(int i=2; (i*i)<=n; i++){
if(primeList.get(i)){
for(int j = i*i; j<=n; j+=i) primeList.set(j, false);
//i*i 미만은 이미 처리되었으므로 j의 시작값은 i*i로 최적화할 수 있다.
}
}알고리즘 과정
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
자기 자신을 제외한 3의 배수를 모두 지운다. - 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
자기 자신을 제외한 5의 배수를 모두 지운다. - 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
자기 자신을 제외한 7의 배수를 모두 지운다. - 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
시간복잡도
O(N * log log N)
약수와의 관계
사실 우 두 가지 방법은 약수를 구하는데에도 이용할 수 있다.
단일 소수 검사
마찬가지로 root(n)까지 돌며 나누어 떨어지는 수를 탐색한다. 만약 나누어 떨어진다면 나누는 수와 나눈 몫이 결국 약수가 된다.
static long calDSum(int N) {
long result = 0;
for (int i = 1; i * i <= N; i ++) {
if (N % i == 0) {
result += i;
if (i * i != N) {
result += N / i;
}
}
}
return result;
}위 코드는 N의 약수를 모두 더한 합을 계산하는 코드이다.
시간복잡도는 마찬가지로 O(root(N))
에라토스테네스의 체와 유사한 전처리 방식
여러개의 연속된 수의 약수들을 파악할때 에라토스테네스의 체와 유사한 방식으로 처리 가능하다.
for (int i = 1; i <= N; i++) {
for (int j = 1; i * j <= N; j++) {
A[i * j] += i;
}
}마찬가지로 A라는 배열에 각 N의 약수들의 합을 저장하는 코드이다.
시간복잡도는 O(N * log N) (조화급수에 의하여)
https://stackoverflow.com/questions/25905118/finding-big-o-of-the-harmonic-series
파이썬 실제 코딩
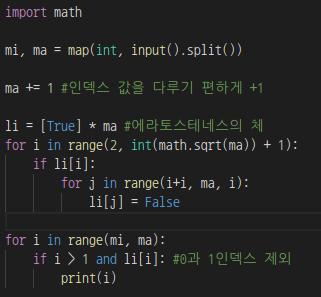
1은 소수에서 제외되니까 주의하자
