Data structure - 해시 맵(해시 테이블)

Solf·2023년 2월 2일

자료구조

목록 보기

6/9

개념

_참고로 해시(Hash)는 다지다의 의미가 있다.

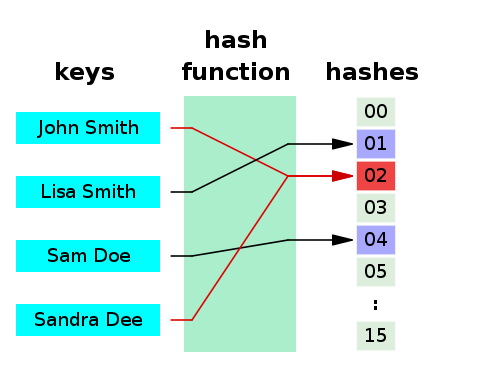
해시 테이블 또는 해시 맵은 키를 값에 매핑할 수 있는 구조인 연관배열추상자료형(ADT)을 구현하는 자료구조다.
대부분의 연산이 O(1)시간복잡도에 해결된다는 점이 특징이다.

왼쪽 Keys 중간이 Hash Function 오른쪽이 Hashes(buckets)

해시 함수란 임의 크기 데이터를 고정 크기 값으로 매핑하는데 사용할 수 있는 함수를 말한다.

# 여기서 화살표가 해시함수기능
ABC -> A1
1324BCX -> CB
ADF234S -> D5

해시테이블을 인덱싱하기 위해 이처럼 해시 함수를 사용하는 것을 해싱(Hashing) 이라고 한다.
사용처는 최적검색이 필여한 분야에 사용되며, 심볼테이블등의 자료구조를 구현하기에도 적합하다. 이외에도 체크섬, 손실 압축, 무작위화 함수, 암호등과 관련이 깊다.

bucket

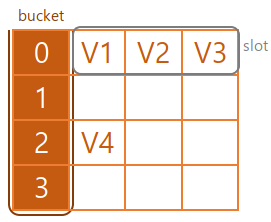
버킷은 내부적으로 해시함수로 해싱된 인덱스 주소를 의미하는데(그림에서 갈색) 하나를 bucket 복수개일 시 buckets라고 표현하기도 한다.

성능 좋은 해시 함수의 특징들

해시 함수 값 충돌의 최소화
쉽고 빠른 연산
해시 테이블 전체에 해시 값이 균일하게 분포
사용할 키의 모든 정보를 이용하여 해싱
해시 테이블 사용 효율이 높은 것

버킷의 동적관리
기본적으로 파이썬과 자바 모두 데이터의 개수에 따라 버킷의 개수를 동적으로 늘려가며 사용한다.
자바의 경우 최대 버킷의 개수는 2^30개이다. 이 한도 내에서 밀도(로드팩터)가 3/4를 넘어가는 시점에 버킷의 크기를 2배씩 늘려가며 지수의 형태로 관리한다.

자바의 경우 HashMap의 키값은 불변 객체(래퍼 or 스트링) 사용을 추천한다. 물론 사용자가 만든 객체를 키로 사용할 수 있지만 어떻게 해시값을 가져올지(hashCode())와 충돌시 equals로 구분하기에 equals()를 override해줘야한다.

실수하기 쉽기에 조금 더 자세히 적자면 Object.hashCode()는 기본적으로 객체의 메모리 주소를 기반으로 정수를 반환한다. Object.equals()는 메모리 주소를 기반으로 저장한다. 그렇기에 override가 없다면 기본 기능을 사용해 아래와 같은 예상치 못한 동작이 일어날 수 있다.

static class Point {
	int x;
    int y;

	public Point(int x, int y) {
    	this.x = x;
        this.y = y;
        }

}
        
import java.util.HashMap;

public class Main {
    public static void main(String[] args) {
        HashMap<Point, String> map = new HashMap<>();

        Point p1 = new Point(1, 2);
        Point p2 = new Point(1, 2);

        map.put(p1, "First Point");

        System.out.println(map.get(p2)); // null 출력 (문제 발생)
    }
}

따라서 오버라이드를 밑처럼 진행하면 정상출력된다.

        @Override
        public int hashCode() {
            return Objects.hash(x, y);
        }

        @Override
        public boolean equals(Object o) {
            return this.x == ((Point) o).x && this.y == ((Point) o).y;
        }

따라서 분해해서 이은 String을 키값으로 쓴다면 좀 더 편하게 자바에 의존할 수 있다. (Collection 클래스도 이미 위 메서드들을 구현해두긴 하지만, 만약 객체의 값을 마음대로 수정하면 해시값이 바뀔 수 있다. 즉 불변객체로 하는걸 권장한다.)

해싱 충돌

해싱은 데이터를 추상화하기에 다른 데이터를 넣었음에도 같은 해쉬를 가지게 되는 충돌이 일어난다.
이는 생각보다 쉽게 일어나는데, 이를 생일 문제로 생각해보자. 생일은 윤년제외 365개인데 여러 사람이 모였을때 생일이 같을 확률은 비둘기집 원리에 따라 366명 이상 모여야 일어나는 일같다. 그러나 실제로는 23명만 모여도 50%를 넘고 57명만 모이면 99%를 넘어선다.

개별 체이닝 / 오픈 어드레싱

해싱 충돌이 일어났을 때 어떤 식으로 처리할까?

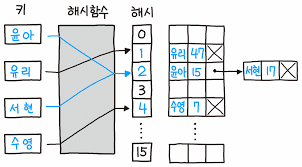
먼저 개별 체이닝 방식을 알아보자.
개별 체이닝(Separate Chaining)방식은 충돌 시 값들을 연결 리스트 방식으로 연결하여 해결한다.

특징

간단한 알고리즘 만으로 구현해 인기가 많다.
해시 테이블 구조의 원형이며, 가장 전통적인 방식

시간 복잡도
잘 구현한 경우, 대부분의 탐색은 O(1)이지만 최악의 경우 모든 해시 충돌이 발생하면 O(n)이 된다.

자바
자바의 HashMap, HashSet은 충돌 시 개별 체이닝 방식을 사용한다. 최초에는 위에 설명한 liked list로 구현했으나 자바8부터는 개수가 많다면 tree를 사용해 성능을 더욱 높였다. 즉 적을때는 linked list 많을때는 tree를 쓴다.
Open Addressing의 데이터 삭제시 효율적인 처리가 어렵다는 점을 고려해서라고 합니다.

다음은 오픈 어드레싱 방식이다.

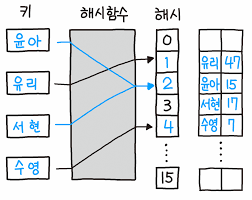
오픈 어드레싱(Open Addressing)방식은 탐사를 통해 빈공간을 찾아 저장하는 방식이다.

특징

무한정 저장할 수 있는 체이닝 방식과 달리 전체 슬롯의 개수 이상은 저장 불가.
개별 체이닝 방식과 달리, 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장이 없다.
선형탐사의 문제점으로 데이터가 고르게 분포되지 않고 뭉치는 경향이 있는데 이를 '클러스터링(Clustering)'이라고 한다. 이는 탐사시간을 오래걸리게 하며 해싱 효율을 떨어뜨린다.
데이터가 버킷사이즈보다 큰 경우, 즉 기준이 되는 로드 팩터 비율을 넘어서면 그로스 팩터(Growth Factor)의 비율에 따라 더 큰 크기의 또 다른 버킷을 생성해 여기에 새롭게 복사하는 리해싱(Rehashing)작업이 일어난다. (동적 배열에서 공간이 가득차면 더블링으로 새롭게 복사해 옮겨가는 과정과 유사)

파이썬
파이썬의 딕셔너리 자료형은 해시 테이블로 구현되어 있다.
파이썬의 해시테이블은 충돌 시 오픈 어드레싱 방식을 사용한다.
CPython 주석에 따르면 이유는 체이닝 시 malloc으로 메모리를 할당하는 오버헤드가 높아 오픈 어드레싱을 택했다고 한다.

각 방식의 성능비교

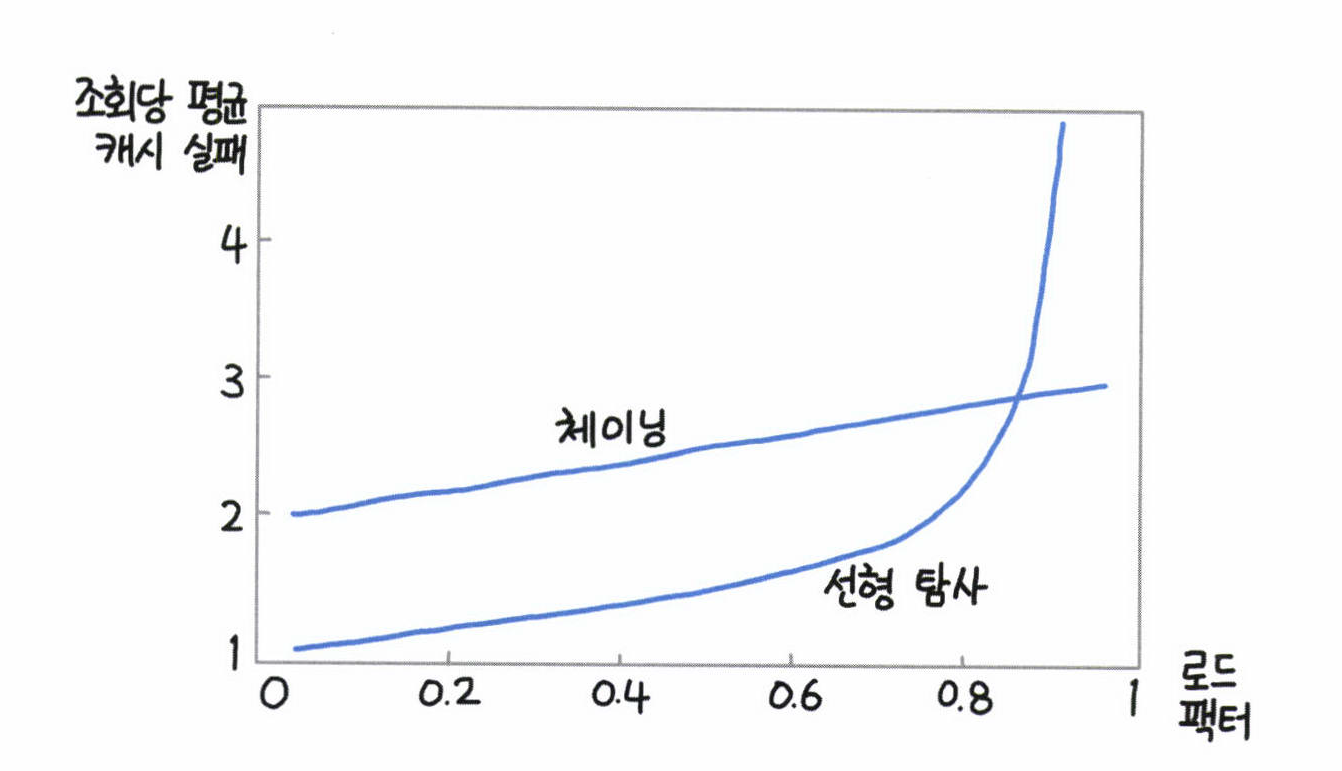
위 그래프에서 성능 차이를 확실하게 보여주는데 루비나 파이썬 같은 모던 언어들은 오픈 어드레싱 방식을 택해 성능을 높이는 대신, 로드 팩터를 작게 잡아 성능 저하 문제를 해결한다.
실제로 파이썬 로드 팩터는 0.66으로 자바보다 작으며 루비는 0.5로 훨씬 작다. 둘 모두 오픈 어드레싱 방법을 택한다.
(c++: 개별 체이닝, 자바: 개별 체이닝, 고(Go): 개별 체이닝, 루비: 오픈 어드레싱, 파이썬: 오픈 어드레싱)

비둘기집 원리

비둘기집 원리란 n개의 아이템을 m개의 컨테이너에 넣을 때, n>m이라면 적어도 하나의 컨테이너에는 반드시 2개 이상의 아이템이 들어 있다는 원리를 말한다.

로드 팩터

load factor = n/k
로드 팩터(Load Factor)란 해시테이블에 저장된 데이터 개수 n을 버킷의 개수 k로 나눈 것이다. 로드 팩터를 보고 해시함수를 재작성 해야할지 테이블의 크기를 조정해야할지 결정하며, 해시함수가 키들을 잘 분산해주는지 말해주는 효율성 측정의 기준이 되기도 한다.