그래프(Graph)

---

그래프는 정점(vertex)와 간선(edge)으로 구성된 자료구조(원소 사이 다:다 관계를 표현하는 자료구조)

수학적으로 G = (V, E) 로 표현하기도 한다.

용어
인접: 두 정점을 연결하는 간선이 있을때 두 정점이 인접되어있다고 한다.(정점의 관점)
부속: 위 연결하는 간선을 두 정점에 부속되어 있다고 한다.(간선의 관점)
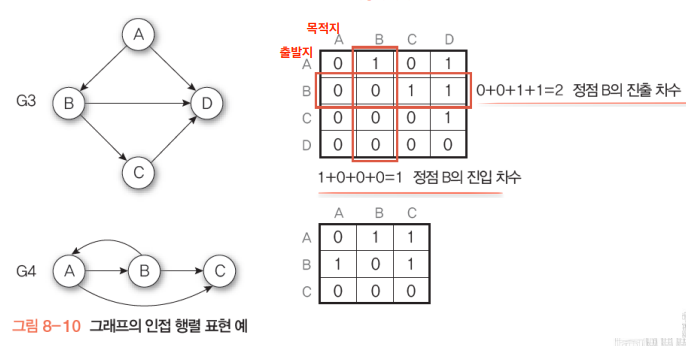
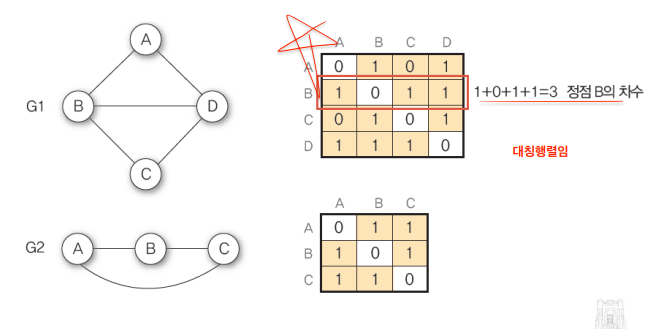
차수(degree): 정점에 부속되어있는 간선의 수(트리에서는 자식노드의 수였음)
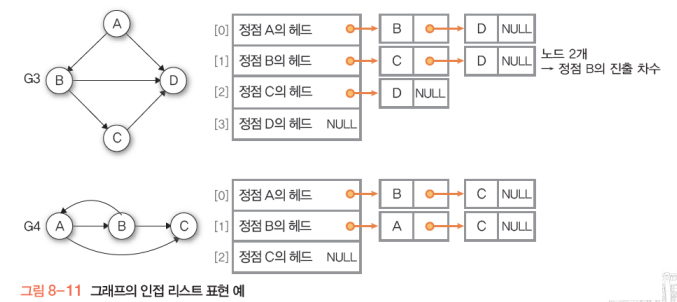
방향그래프에서는 진입차수/진출차수로 방향에 따라 두 종류로 나뉨
DAG: 방향그래프이면서 사이클이 없는 그래프
연결 그래프: 고립된 정점이 없는 그래프
단절 그래프: 고립된 정점이 있는 그래프
경로(path): 출발 정점부터 목적지 정점까지 갈 수 있는 간선을 나열한것
경로길이: 경로를 구성하는 간선의 수
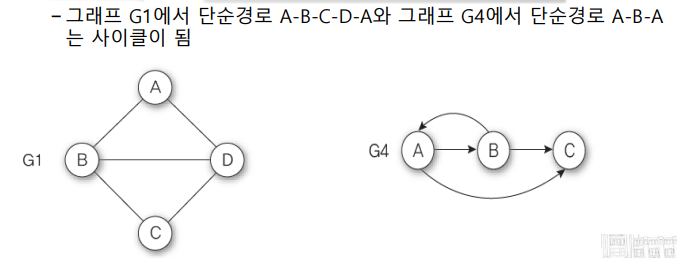
단순경로: 모두 다른 정점으로 구성된 경로(같은정점을 두번 방문하지 않는 경로)
사이클(cycle): 단순경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로

코드구현방법
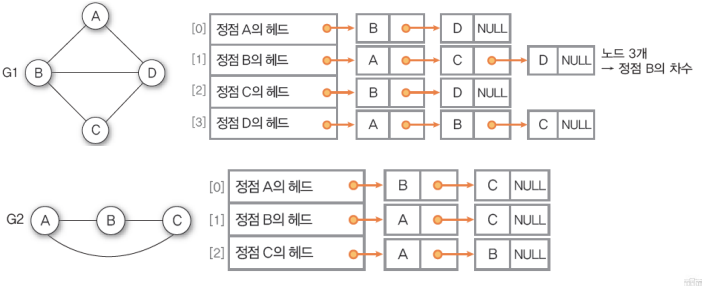
인접행렬을 주로 활용한다.


인접리스트로도 구현가능하다.

탐색방법

• DFS : 깊이우선탐색(스택 활용)
• BFS : 너비우선탐색(큐 활용)

무방향/방향 그래프

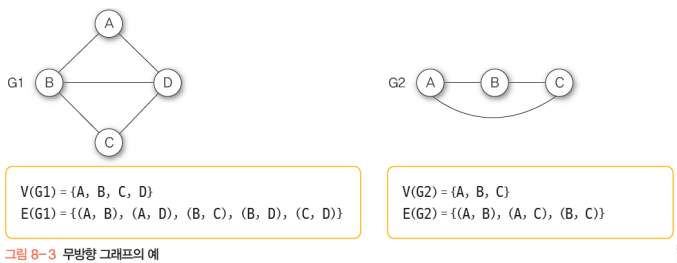
무방향 그래프

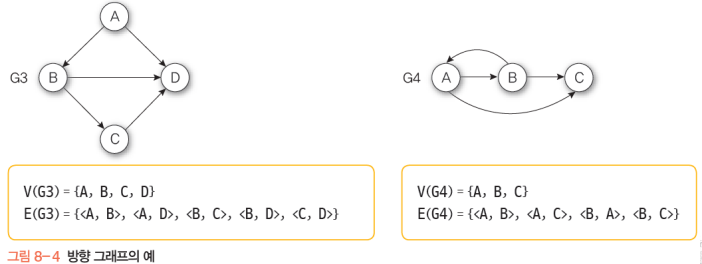
방향 그래프

완전 그래프

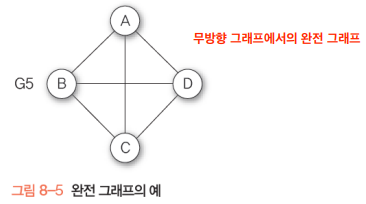
각 정점에서 다른 모든 정점을 연결해 최대로 많은 간선 수를 가진 그래프

부분 그래프

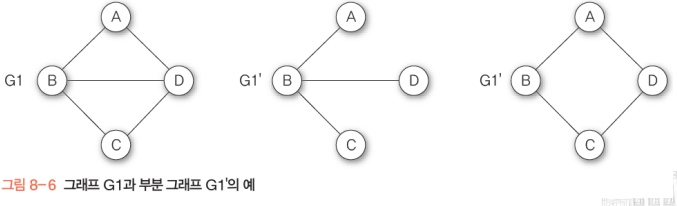
원래의 그래프에서 정점이나 간선을 일부만 제외한 그래프

가중 그래프

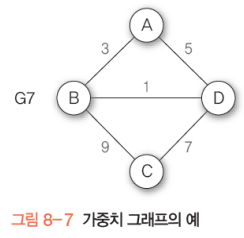
정점을 연결하는 간선에 가중치(weight)를 할당한 그래프

신장트리

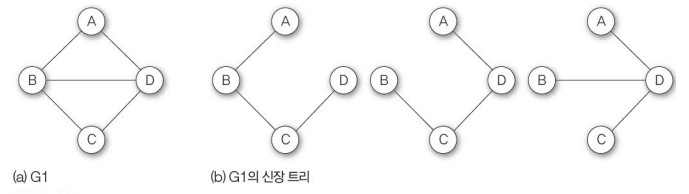
신장트리: n개의 정점으로 이루어진 무방향 그래프 G에서 n개의 모든 정점과 n-1개의 간선으로 만들어진 트리(사이클없음)
간선을 최소로 이용하여 모든 정점을 연결한 그래프이다.

깊이/너비 우선 신장 트리

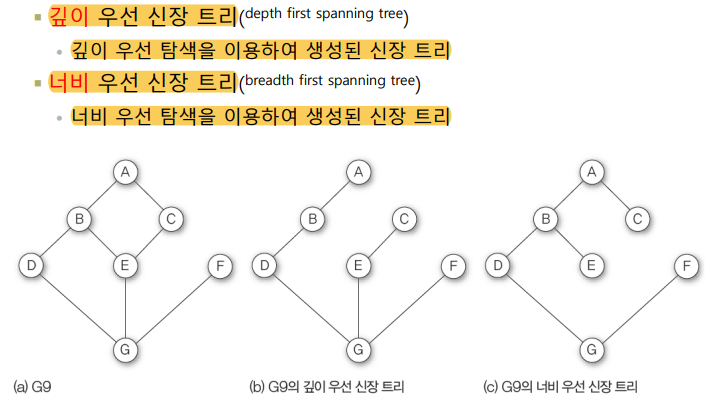
최소비용 신장트리

무방향 가중치 그래프에서 신장트리를 구성하는 간선들의 가중치 합이 최소인 신장트리

최소비용 신장트리를 만드는 대표적인 알고리즘

• 크루스칼의 알고리즘
  

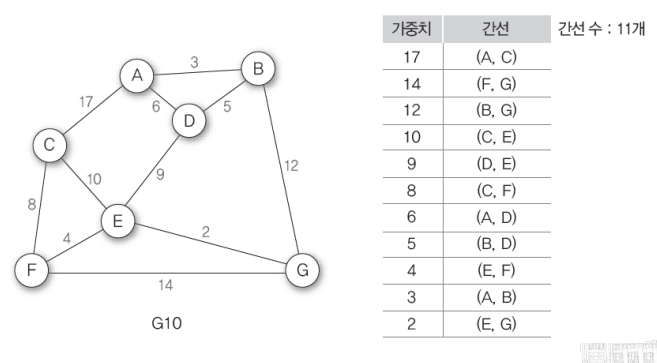
1. 기존의 그래프에서 가중치에 따라 모든 간선을 내림차순으로 나열-> 가중치가 큰 간선부터 고립되는 정점이 생기지 않게 제거 -> 간선이 n-1개 남을때까지 반복
2. 가중치에 따라 모든 간선 오름차순 나열 -> 가중치가 작은 간선부터 연결해 사이클이 생기지 않도록 배치 -> 간선이 n-1개가 될때까지 반복

• 프림의 알고리즘
  간선을 정렬하지 않고 하나의 정점에서 시작해 트리를 확장해나가는 방식
  

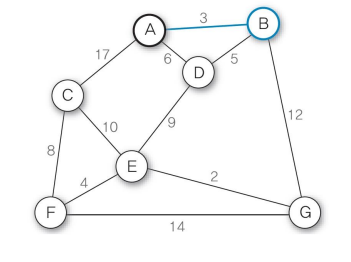
최단경로

현대 네비게이션에서도 활용하는 알고리즘으로 주로 가중치 인접행렬과 다익스트라 알고리즘을 활용해구한다.

가중치 인접 행렬

다익스트라 스도코드

트리(Tree)

---

트리는 그래프와 같이 노드와 노드간을 연결하는 간선으로 구성된 자료구조 (1:n 관계의 비선형 자료구조)
트리는 그래프 중에서도 특수한 케이스에 해당하는 자료구조이다.
부모-자식 관계가 성립하기 때문에 계층형 자료구조라고도 한다.

용어정리
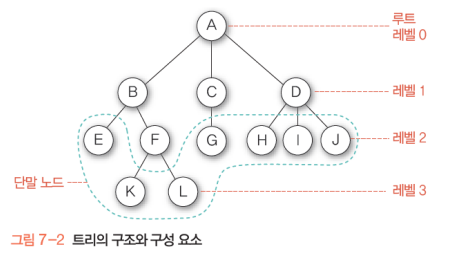
node: 트리의 원소
root node: 트리의 시작 노드(레벨 0)
leaf node: 단말노드(자식이 없는 노드들)
edge(간선): 노드를 연결하는 선
parent child: 연결된 노드는 부모자식 관계를 가진다
sibling node(형제노드): 같은 부모노드의 자식노드
subtree: 부모노드와 연결된 간선을 끊어서 생성되는 트리
level(높이): 루트노드로부터의 수직 거리
degree(차수): 자식노드의 수

탐색과 관련된 트리의 종류

트리의 종류 중 탐색과 관련된 유명한 트리들을 정의와 함께 정리한다. 이후 이진트리로 이 응용들을 확인 할 수 있다.

self-balanced tree

self-balanced tree는 루트 노드로부터 가장 깊은 터미널 노드까지의 탐색(= 트리의 높이) 시간 복잡도가 O(log n)을 보장하는 tree이다.

즉 편향트리가 되지 않도록, 높이에 제한을 두어 탐색 시간을 빠르게 해준다.

search tree

특정 키값이 어떤 집합에 속하는지 검색할때 사용하는 tree이다.

이는 trie등을 포함하는 넓은 의미이며 좁은 의미로 각 노드의 키가 왼쪽 서브 트리의 어떤 노드보다 크고, 오른쪽 서브 트리의 어떤 노드보다 작아야한다는 재귀적 정의가 있다.

이진트리

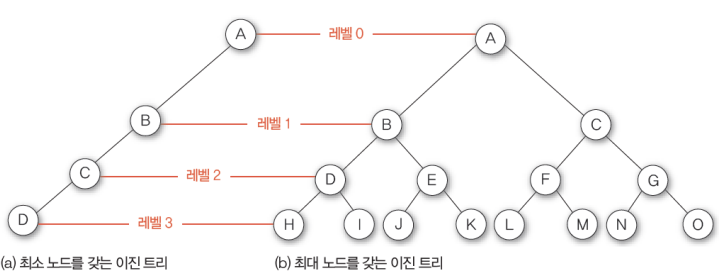
모든 노드의 차수를 2 이하로 제한하여 전체 트리의 차수가 2 이하가 되도록 정의한 것.

이진트리의 특성
노드가 n개일때 간선이 반드시 n-1개
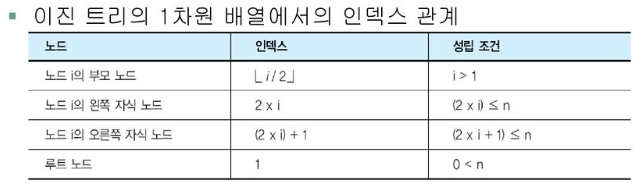
높이가 h인 이진트리가 가질 수 있는 노드 개수는 최소(h+1)개 최대(2^(h+1) - 1)개

탐색방법
-L-R- (-자리들중 어디에 D를 넣어 탐색하냐에 따라 3가지로 나뉜다.)

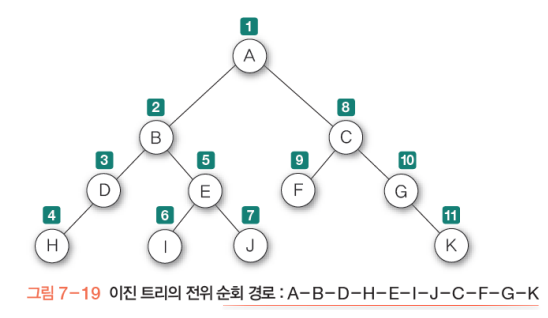
• 전위 순회: D-L-R순 탐색
  

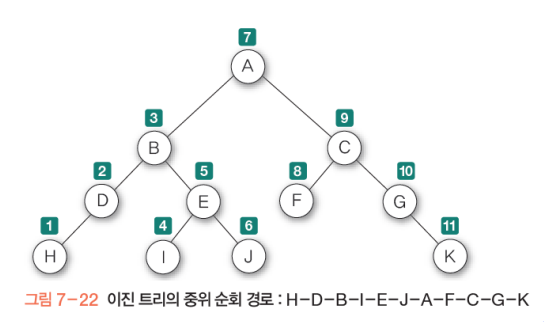
• 중위 순회: L-D-R순 탐색
  

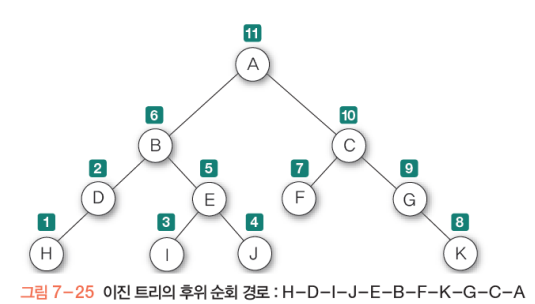
• 후위 순회: L-R-D순 탐색
  

이진트리의 종류

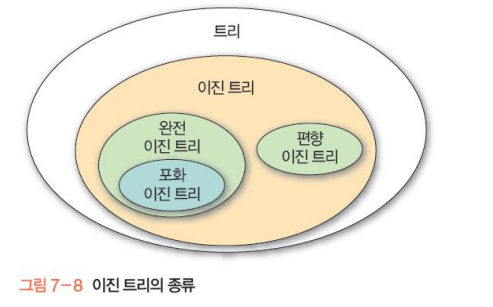
완전이진트리

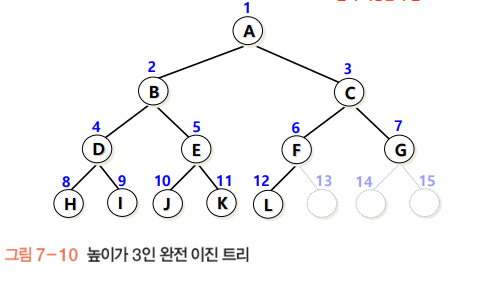
높이가 h이고 노드 수가 n개 일때 노드 위치가 포화 이진트리에서의 노드 1번부터 n번까지의 위치와 완전히 일치하는 이진트리.

완전이진트리는 인덱스 조작이 편리하다는 장점이 있다.(물론 포화이진트리포함)

포화이진트리

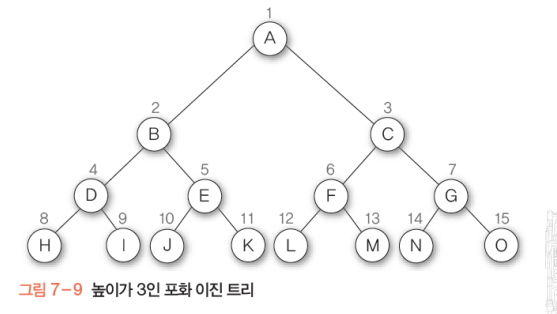
모든 레벨에 노드가 포화상태로 가득 차있는 이진트리.

히프

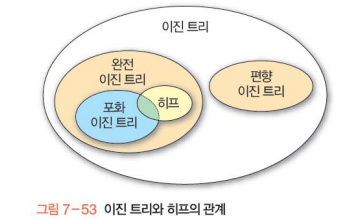
완전 이진 트리에 있는 노드 중에서 키값이 가장 큰 노드나 작은 노드를 찾기 위해 만든 자료구조.

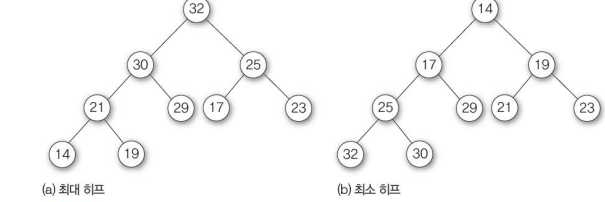
최대히프: 부모노드의 키값 >= 자식노드의 키값(조건) - 루트노드가 가장 커짐
최소히프: 부모노드의 키값 <= 자식노드의 키값(조건) - 루트노드가 가장 작아짐

• 삽입과정
  

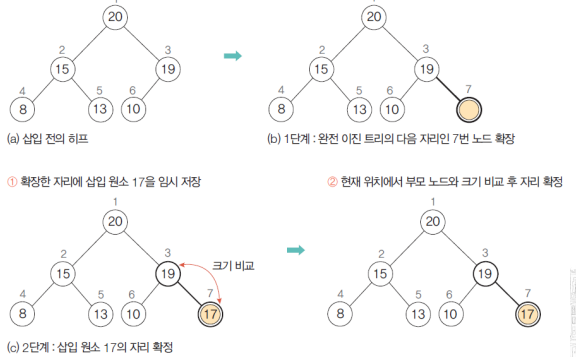
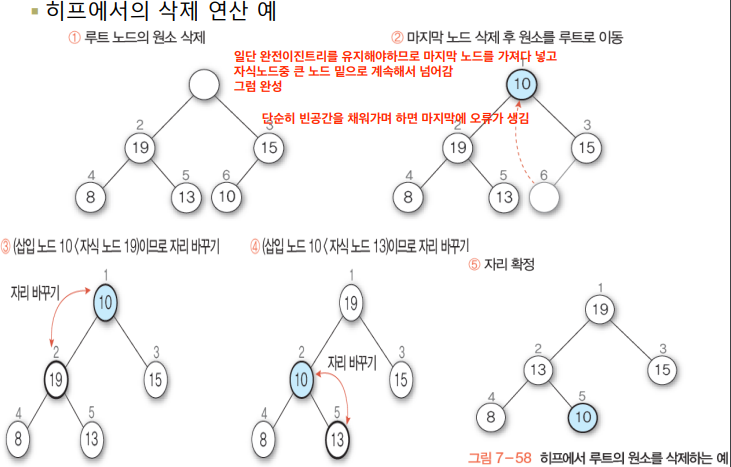
• 삭제과정
  

편향이진트리

이진탐색트리

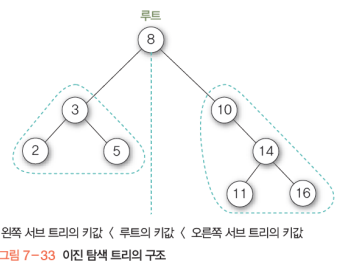
이진트리를 탐색에 용이하도록 원소크기에 따라 노드위치를 정의한 것.
모든 '부모노드가 왼쪽 서브트리의 키값 < 부모노드의 키값 < 오른쪽 서브트리의 키값' 조건을 만족한다.

• 삽입과정

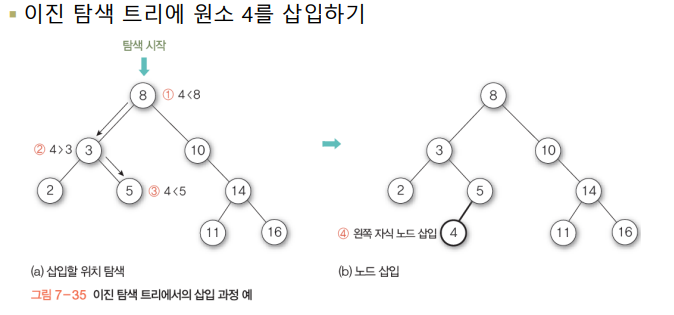
• 삭제과정
  
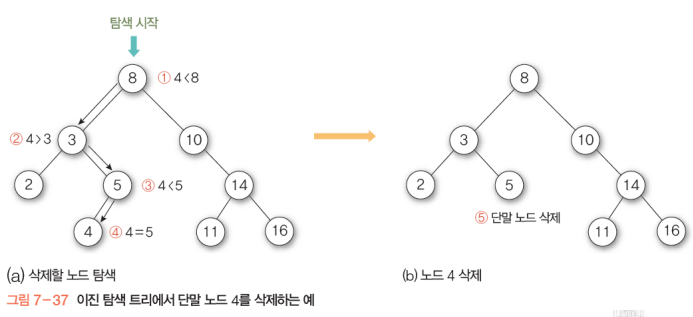
  이때 삭제할 노드에 후계자가 필요하다면 밑과 같은 과정으로 선정한다.

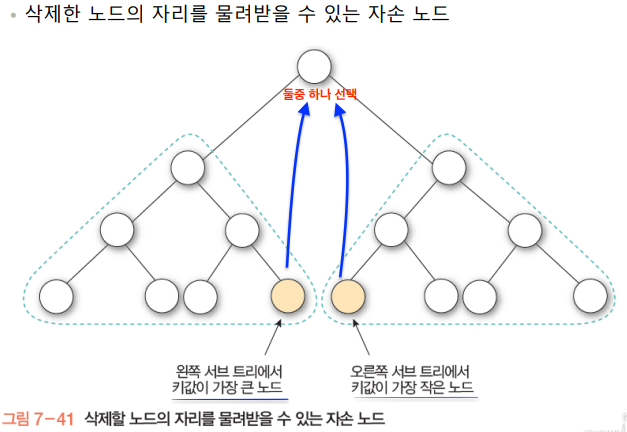
균형이진탐색트리

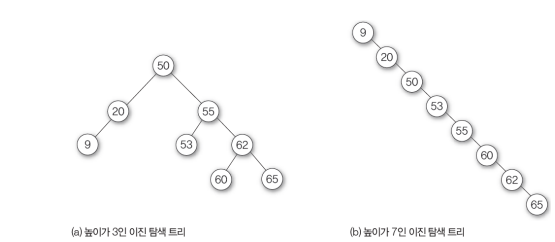
이진탐색트리의 균형이 잘 맞으면 탐색의 성능이 높아지기에 이를 만족하기 위해 만들어진 이진탐색트리
왼쪽이 균형트리이다.

대표적으로 AVL트리가 있다.

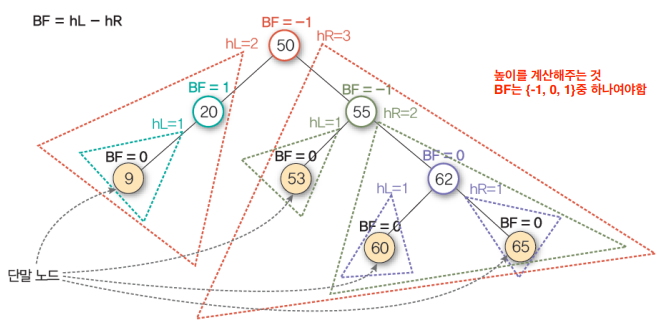
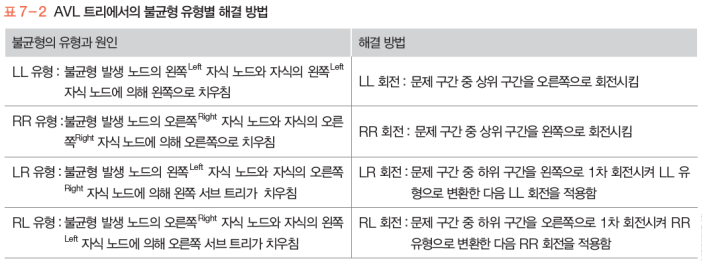
왼쪽 서브트리의 높이(hL)와 오른쪽 서브트리의 높이(hR) 차이(BF, balance factor)가 1 이하인 트리

새로운 노드의 삽입으로 불균형이 발생하면 회전을 통해 해결한다.