수학에서, 좀 더 구체적으로 그래프 이론에서 그래프(Graph)란 객체의 일부 쌍(Pair)들이 '연관되어' 았는 객체 집합 구조를 말한다.
그래프의 역사
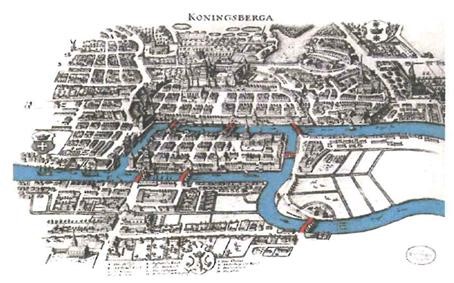쾨니히스베르크의 프라겔 강 다리 지도
18세기 프로이센 공국의 쾨니히스베르크에는 프레겔 강이 흐르고 있었다. 프레겔 강에는 2개의 큰 섬이 있고 이 섬과 도시를 연결하는 7개의 다리가 놓여있었다. 어느날 도시의 시민 한 명이 "이 7개의 다리를 한번씩만 건너서 모두 지나갈 수 있을까?"라는 흥미로운 문제를 냈다.
레온하르트 오일러가 이 문제를 조사하기 시작했다. 이 문제는 도형문제처럼 보이나, 당시까지 알려진 기하학으로는 풀 수 없는 문제였다. 미지의 영역에 그 해법이 있다는 것을 알았다.
이것이 그래프 이론의 시작이다.
오일러 경로
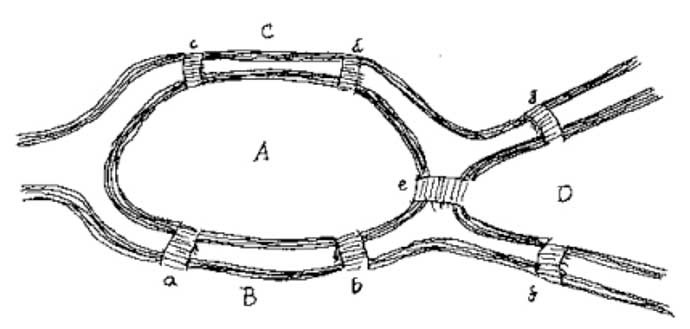오일러가 논문에 직접 그린 쾨니히스베르크 다리 스케치
오일러는 이 문제를 도식화하여 풀었는데, 이는 현대에 이르러 그래프 구조의 원형이 되었다. 그림을 보면 A부터 D까지를 정점(Vertex), a부터 g까지는 간선(Edge)으로 구성된 그래프라는 수학적 구조이다.
오일러는 모든 정점이 짝수개의 차수를 갖는다면 모든 다리를 한번씩만 건너서 도달하는 것이 성립한다고 했다. - 오일러 정리
(정점이 가지는 간선의 수를 차수(Degree)라고 한다.)
이는 수학적으로 증명 되었으며,
모든 간선을 한번씩 방문하는 유한 그래프(Finite Graph)를 일컬어 오일러 경로(Eulerian Trail/Eulerian Path)라고 부른다.
참고로 쾨니히스베르크는 모든 정점이 짝수개의 차수를 갖지 않아(심지어 모두 홀수) 오일러 경로가 아니다.
해밀턴 경로
헤밀턴 경로는 각 정점을 한번씩 방문하는 무향 또는 유향 그래프 경로를 말한다.
해밀턴 경로와 오일러 경로의 차이점은, 오일러는 간선을 기준으로 해밀턴은 정점을 기준으로 한다는 점이다.
꽤나 사소한 차이로 보이지만 해밀턴 경로는 최적 알고리즘이 없는 대표적인 NP-Complete(완전)문제다.
해밀턴 경로 중 원래의 출발점으로 돌아오는 경로는 특별히 해밀턴 순환(Hamiltonian Cycle)이라 한다. 이중에서도 특히 최단 거리를 찾는 문제는 외판원 문제(TSP/Travelling Salesman Problem)로 유명하다.
외판원 문제는 각 도시를 방문하고 돌아오는 가장 짧은 경로를 찾는 문제로 NP-난해 문제이며 이론 컴퓨터과학 분야에 매우 중요한 문제 중 하나이다.
이 문제의 시간복잡도는 도시가 n개일 때 아래와 같다.
부르트포스: O(n!)
DP: O(n^2*2^n)
이베이는 O(1)이라는 재치있는 광고도 있다.
