회로를 설계할 때 어떤 논리회로를 얼마만큼 사용할 것인지는 비용면에서 상당히 중요한 문제이다. 그러나 단순히 입력과 출력에 대한 진리표만 가지고 설계를 하려고 하면 비용을 최소화하는 것이 어려울 것이다. 따라서 이 비용을 최소화하는 과정을 간략화라고 한다.

불 대수

수학에서 명제논리의 연산을 정의한 것이다. 결국 컴퓨터 체계에서 1과 0은 불 대수에서 참과 거짓으로 보아 이를 연산할 수 있도록 하며, 이 연산식을 최소화 하는 것이 회로의 간략화와 연결되는 것이다.

위와 같이 수학적으로 정의되고 있다.

최소항 : 표준 곱의 항 (표준 곱의 항이란 함수의 모든 변수를 표현하는 것)
곱의 합(sum of product, SOP): 1단계는 AND항으로 2단계는 OR항으로 만들어진 논리식 (ex AB + AC)
합의 곱(product of sum, POS): 1단계는 OR항으로 2단계는 AND항으로 만들어진 논리식 (ex (A+B)·(A+C))

카르노 맵

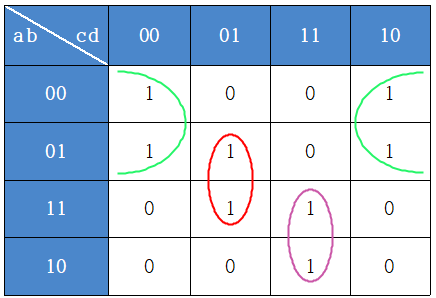
불 대수와 마찬가지로 간략화를 하는 방법으로서 불대수의 법칙을 활용하여 수학적으로 계산하여 간략화하는게 쉽지 않아 카르노 맵이라는 형태로 불대수식을 간략화하는 방법이다.

위와 같은 형태로 입력값에 대한 표를 그려 규칙에 맞게 1들을 묶고 이를 식으로 적으면 간략화가 가능하다.