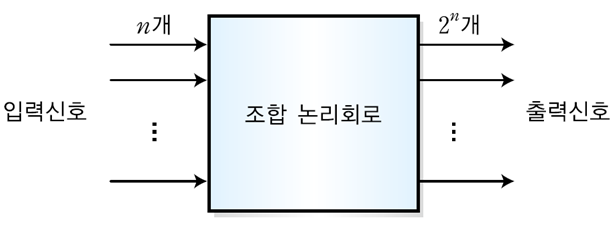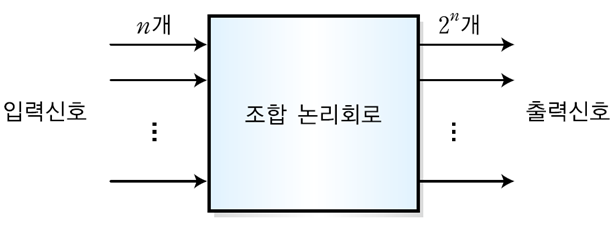
조합논리회로는 AND OR NOT 게이트를 조합하여 구성한 논리회로로서 단순히 입력값에 따라 출력값을 반환한다.(순서논리회로는 순서논리회로는 상태(이전 입력값에 따른)에 따라 값이 변한다.)
가산기
반가산기(Half Adder)
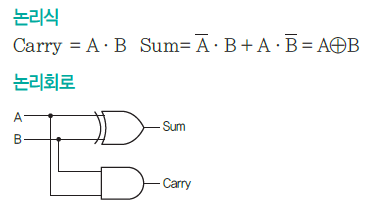
1비트 덧셈을 연산할 수 있다. carry는 자리올림을 sum은 덧셈결과를 의미한다.
가산기(Full Adder)

반가산기 2개를 이어붙여 만들며 자리올림값을 입력으로 받을 수 있다.
C_in : 자리올림 입력값
C_out : 자리올림 결과값
병렬가감산기
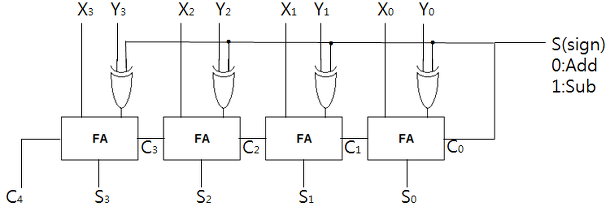
가산기를 병렬로 연결하여 원하는 비트(자리수)만큼 덧셈을 가능하게 만든 것이다. 또한 2의 보수방식으로 감산까지 가능한 S(sign)비트가 있다.
이때 C_3,2,1,0은 줄줄히 연결되어 리플래더(댓글처럼 연결된 선)이면서 연산시간에 치명적인 영향을 주는데 때문에 이를 크리티컬 패스라고 하기도 한다.
고속가산기
회로가 복잡하여 박스처리하기에 그림은 생략하였다.
병렬가산기는 위에서 언급하였듯 자리올림수에 의해 속도가 매우 느리다. 때문에 이를 해결하기 위한 캐리예측가산기(carry-look-ahead-adder, CLA)를 활용한다. 이는 자리올림수만을 먼저 연산하여 시간을 대폭 줄여준다.
비교기
두 수의 크기를 비교하는 비교기는 자체적인 회로를 만들 수도 있으나, 이는 비교하는 숫자의 크기에 따라 회로가 비효율적이게 된다. 때문에 가산기를 활용하여 대체된다.
A-B의 값이 음수인 경우: B>A
A-B의 값이 양수인 경우: A>B
A-B의 값이 0인 경우: A=B
인코더/디코더
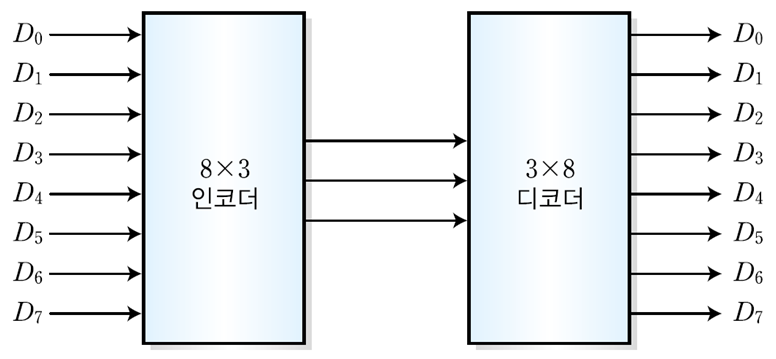
컴퓨터는 인간들이 사용하는 서로 다른 정보를 2진코드로 변환하여 사용해야 한다. n비트의 2진 코드와 최대 2^n 개의 서로 다른 정보를 상호 번역 해주는 것이 인코더와 디코더다.
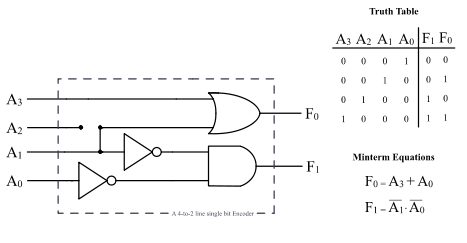
인코더 : 서로다른 정보 -> 2진코드 (이미지의 8 x 3과 같이 2^n x n의 형태로 이름이 붙는다)
위에 보이듯 서로다른 정보 A_3~A_0 중에서 하나의 정보가 들어오면 그 값의 번호에 따라 이진수로 변환해준다. A_0 -> 0 0, A_1 -> 0 1
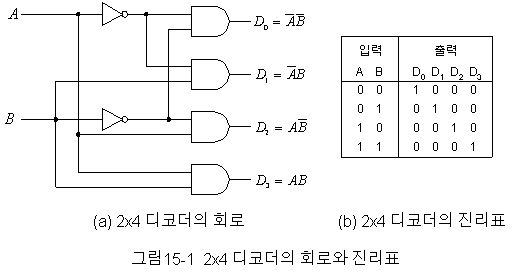
디코더 : 2진코드 -> 서로다른 정보 (이름은 n x 2^n 형태)
들어온 이진수에 따라 서로다른 정보에 해당하는 출력을 준다.
0 0 -> D_0, 0 1 -> D_1
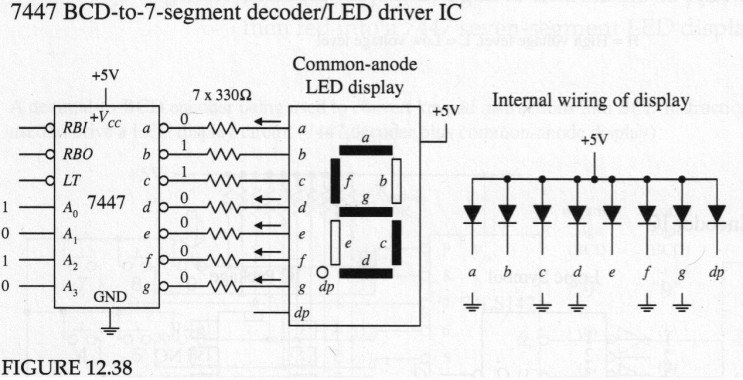
대표적인 예시로 세그먼트 디코더가 있다.
멀티플렉서/디멀티플렉서
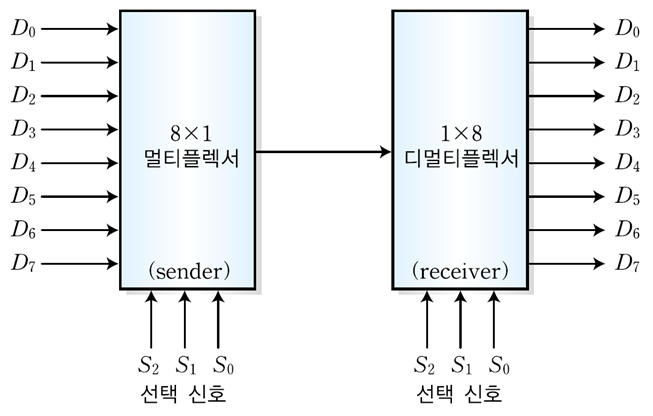
여러개의 입력선들 중 하나를 선택해서 출력선에 연결하는 조합논리회로. (기차의 선로를 바꿔주는 역할이라고 보면 이해가 쉽다.) 멀티플랙서와 디멀티플랙서는 줄여서 MUX DEMUX라고 부른다.
MUX : 선택신호에 따라 입력선을 선택해주는 회로이다. 이미지와 같이 선택신호 (select signal)을 받는데 이 값에 따라 D_0~D_7중 연결할 선을 선택하게 된다. ex) 000 -> D_0 001 -> D_1
DEMUX : 선택신호에 따라 출력선을 선택해주는 회로이다. 선택신호에 따라 D_0~D_7을 선택하여 입력받은 값을 전달한다. ex) 000 -> D_0 001 -> D_1
코드 변환기
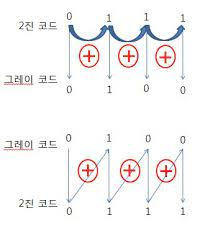
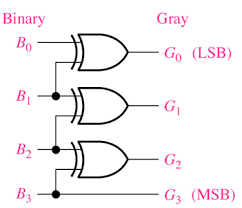
코드에는 앞에서 공부했듯 정말 다양한 종류가 있다. 대표적으로 그레이코드 변환기를 알아보자면 우리가 직접 변환할때 적용했던 과정과 동일한 회로도를 가진다.
패리티 발생기/검출기
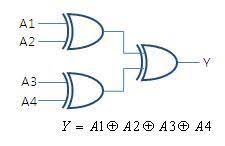
짝수 패리티의 경우 모든 입력값을 XOR로 묶는다.
홀수의 경우 마지막에 not을 하나 붙여주면 된다.