
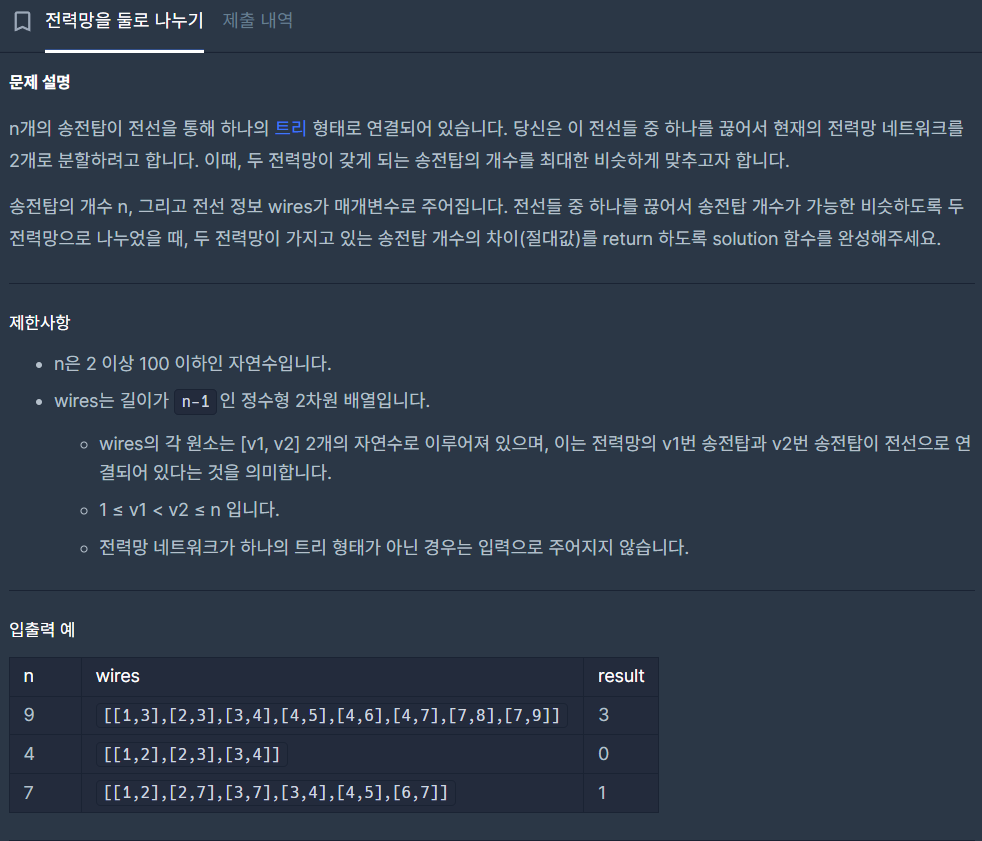
wires 리스트에서 차례대로 전체 전선 중 하나씩 끊는 모든 경우를 고려한다.
전선 하나를 끊어서 쪼개진 두 트리의 크기를 구하여 절댓값 차이를 계산한다.
해당 절댓값 차이가 지금까지의 최소 절댓값 차이(min_diff)보다 작다면 갱신한다.
최종 최소 절댓값 차이를 리턴한다.
- 트리 구현: 딕셔너리 {} 로 구현, 양방향으로 연결!
- 트리의 크기를 구하는 방법: DFS(Depth First Search)로 구현 -> count_all_nodes()
- 딕셔너리에 존재하지 않는 key-value 추가하는 방법: dict[key] = [value]
- 딕셔너리에 존재하는 key에 대한 value만 추가하는 방법: dict[key].append(value)
- 딕셔너리에 특정 key에 대한 value 리스트 얻는 방법(만약 해당 key 없다면 빈 리스트[] 반환): dict.get(key, [])
def count_all_nodes(tree, node, visited=None): # depth first search, 특정 노드에 연결된 모든 하위 노드들의 개수를 세어 리턴하는 함수
if visited is None:
visited = set() # visited가 없으면 집합 만들기
visited.add(node) # node 방문처리하기
count = 1 # 나 자신(node) 세어주기
for child in tree.get(node, []): # node의 모든 자식노드들에 대해
if child not in visited: # 방문 안한 자식노드에 대해서만 재귀호출
count += count_all_nodes(tree, child, visited) # 자식노드 갯수 리턴된 것 누적하기
return count # 누적된 모든 자식노드 갯수 리턴
def solution(n, wires):
min_diff = 9999
for i in range(0, len(wires)): # i 는 이번 차례에 끊을 전선 인덱스
tree = {}
v1 = 0
v2 = 0
for j in range(0, len(wires)):
if j == i: # 끊을 전선이라면
v1 = wires[j][0]
v2 = wires[j][1]
continue # 아래 과정 패스하고 다음 전선 확인
# j0 -> j1 방향 추가
if wires[j][0] in tree: # 해당 key가 tree에 이미 존재한다면
tree[wires[j][0]].append(wires[j][1]) # 해당 key에 value 추가
else: # 존재하지 않는 key라면
tree[wires[j][0]] = [wires[j][1]] # 새롭게 추가
# j1 -> j0 방향 추가 (트리는 양방향으로 연결해야 함)
if wires[j][1] in tree: # 해당 key가 tree에 이미 존재한다면
tree[wires[j][1]].append(wires[j][0]) # 해당 key에 value 추가
else: # 존재하지 않는 key라면
tree[wires[j][1]] = [wires[j][0]] # 새롭게 추가
# print(tree)
# 트리 완성되었다면 끊은 전선의 두 노드(v1, v2) 기준으로 쪼개진 두 트리의 크기 체크하기
if len(tree.get(v1, [])) == 0: # 만약 자른 노드가 제일 끝 노드여서 트리에 존재하지 않는다면
len_1 = 1 # 길이를 1로 (노드 하나 혼자 존재함)
else:
len_1 = count_all_nodes(tree, v1)
if len(tree.get(v2, [])) == 0: # 만약 자른 노드가 제일 끝 노드여서 트리에 존재하지 않는다면
len_2 = 1
else:
len_2 = count_all_nodes(tree, v2)
# print(len_1, len_2)
if abs(len_1 - len_2) < min_diff: # 현재 최대 차이보다 더 작다면 갱신 (차이가 작은 것은 곧 전력망을 가장 비슷하게 잘랐다는 의미)
min_diff = abs(len_1 - len_2) # 절댓값
return min_diff